从“数量比”到“份数比”
——“分数的再认识(一)”教学实录与赏析
◇执教/张 丹 赏析/麻永侃
一、回忆整数概念,引出分数
(一)以数4 为例,唤起数概念间的联系。
师:数学跟数有关。我先用“4”说一件事:(在黑板上摆4 个磁扣)我有4 个磁扣。谁能换一个角度,用“4”再说一件事?
生:有4 个物体。
师:换一个角度,“4”仅仅表示4 个物体吗?老师给你个提示:咱们的年龄之间也存在4。
生:4 倍,老师的年龄是我的4 倍。
……
(二)引出分数,用“讲故事。
(一名学生上台操作,将圆形纸片对折,再对折)
师:对折是为了什么?(生答“平均分成2份”)然后呢?(生答“再对折”)请把它的画出来。(学生把其中的1 份画上斜线)
【赏析】数是一种抽象的概念,要对数有丰富的理解,必须清楚理解各数之间的关系。如:4 比2 大但比5 小;4 是1 与3 的合成,也是2 和2 的和;1 只青蛙有4 条腿……要求学生能理解数及其表征方式,并且探索各类数之间的关系,如此渐渐变化,对数的直觉便在对整数、分数、小数及百分率等的认识中发展。在这节课上,张丹老师有意识地让学生在表示出圆的后,用“”讲一个生活中的故事,发散学生的思维,以丰富学生对分数的理解。
二、引导探究,推动从“数量比”到“份数比”的转化
(一)探究1:数量比——表示出4 个磁扣的。
1.给出任务。
师:我先给一个任务。(指黑板上的磁扣)这里有4 个磁扣,用它们可以表示出吗?在练习本上表示出来,用1 个小圆表示1 个磁扣,要让别人一眼就能看出你表示的。
2.学生尝试表征。
3.反馈交流。
师:谁愿意上来分享自己的想法?
生1 在黑板上画出4 个小圆。
生2 在生1 的图上改,如图1:

图1
师:她这么一画,我们很容易就看出来,确实一共有4 个,把它平均分成4 份,1 个就是全部的。
(二)探究2:份数比——表示出多个磁扣的。
1.给出任务。
师:学数学得想新的事儿,不能总等着老师告诉你接下来该干什么了。我们先表示出了1 个东西的,又想到用4 个磁扣也能表示出,接下来,你会想到什么事儿?
2.学生尝试表征。
3.反馈交流。
(教师出示作品1,如图2)

图2
师:不是8 个磁扣吗?为什么写一个“4 组”?为什么要分成4 组?的“4”表示什么?
(学生回答后,教师出示作品2,如图3)

图3
师:(指着图3 中1 份里的3 个磁扣)明明是3 个,怎么是?是谁的?
生:12 个磁扣,平均分成4 组,每组3 个,取其中的1 组就是。
师:总数中有4 个的、有8 个的、有12 个的……数学的事儿永远也说不完,磁扣永远也摆不完,谁能用一句话概括到底什么是?
师:能概括黑板上的所有东西吗?
生:其实也不一定都是4 的倍数。
【赏析】作品1、作品2 分别用表示,对三年级学生来说并不困难,他们可以用数量关系代替份数,用整数计数的思维帮助理解。到了五年级,要学会用份数表达,只要平均分成4 份,取1 份,至于这1 份中是1 个还是多个,并不重要。
(三)探究3:份数比——表示出“不是4 的倍数”的 。
1.给出任务。
2.学生尝试表征。(2 个磁扣用2 个圆表示)
3.反馈交流。
(生1 上台画出自己的作品,如图4)
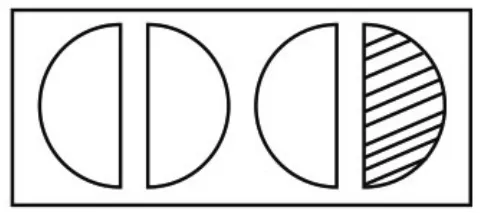
图4
(师生配合,用圆片演示过程,如图5)
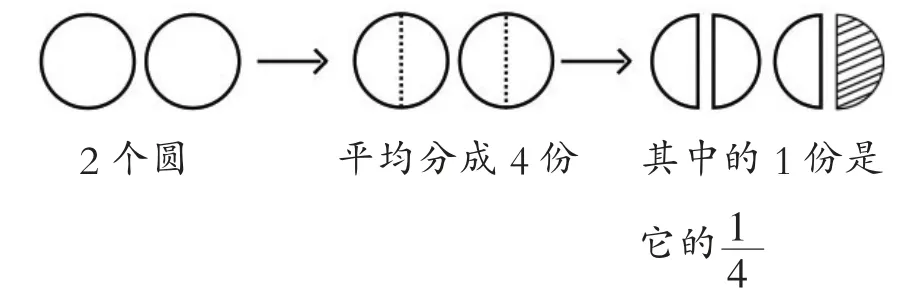
图5
生:能。
【赏析】通过前面的探究,学生好像对有了较好的理解。但从课堂的反馈看,学生对的理解存在一些有意思的想法,比如,他们觉得如果整体是2 个、5 个等,不能找到,理由是有余数。张老师以2 个圆为例,通过图形表征,让学生明白,只要平均分成4 份,取1 份,这1 份不论是多少,代表的都是,从而突破认知难点。
(引导同桌之间讨论: 到底把什么平均分成4 份,1 份就是)
生1:不管多少个物体,只要把它们平均分成4 份,然后中间有一部分明显表示出来的,就叫。
师:数学书上说的是:把“一个整体”平均分(将黑板上“4 的倍数”改为“一个整体”)。这个整体的数量可能是4 的倍数,也可能不是,只要把这个整体平均分成4 份,其中的1 份就是它的。现在我们对分数有了新的认识,今天这节课就是对分数进行再认识。
【赏析】学生对分数的理解不是一步到位的,而是逐步深入、螺旋上升的。张老师重视学生形成概念的整个过程,让学生在经历找整体是不同个数的的过程中,不断尝试概括什么是。在学生的新知与已有知识和经验的冲突中,不断修正,逐步形成概念,完善认识。
师:(指图6)你们看这幅图,它能不能代表你心目中所有东西的?

图6
1.学生想象。
2.学生操作。
3.反馈交流。
(4 个学生上台,将几幅图按以下方式操作后,进行对照比较)
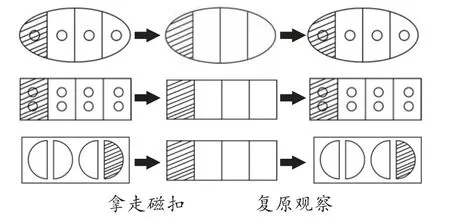
图7
4.小结。
师:所以,不管是什么东西,只要平均分成4 份,1 份就表示这个东西的,你们同意吗?
【赏析】有调查发现,绝大多数学生均不能从“数量比”直接转化为“份数比”,但是如果能够将所给图形结构化一些,便会有一部分学生产生转化;如果结构化更加明显,如画分割线,大多数学生能够直接提炼出“份数比”。为了推动从“数量比”到“份数比”的转化,张老师从整体是4 个到多个再到2 个,让学生通过想象、画图表征等一系列活动,能够自主寻求并找出图形分割的共同点,从而对分数有进一步的认识。
三、再次引导探究,进行部分与整体的推算
师:到这儿,我们对分数已经有更多认识了,最后还有点时间,和大家做一个游戏。
(一)确定部分:如图8,阴影部分是多少?
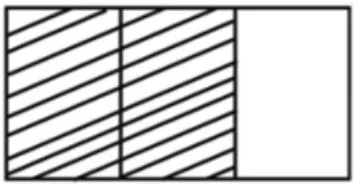
图8
师:你心里随便想一个数,为了交流方便,这个数是整数。你想想,它的是多少?
生:6。
生:2。
生:18。
生:心中想的那个数大小不同。
师:大家心里想的那个表示整体的数不同,同意吗?
生:同意。
(二)推算整体:整体是多少?
生:是9,因为2 份是6,6 除以2 就是1 份的量,1 份再乘3,就是表示整体的数。
(三)理解分母、分子的含义。
生:平均分成3 份,取2 份。
(四)尝试概括什么是分数。
师:现在我们再改造改造,什么叫分数?
(师生共同得出: 把一个整体平均分成4 份也行,3 份也行,书上说的是若干份,这样的1 份或几份,我们就把它叫作分数)
【赏析】给出分数的图的模型,通过想阴影部分是多少,推算整体是多少,把对的理解(平均分成3 份,取2 份)与运算“□÷3×2”挂钩,将对分数的认识转化为一个运算的过程。 这样,心中只要有图,再去理解模型的含义,就能解决实际问题。
四、回顾全课,总结收获
(一)圈收获,说理由。
师:上到这儿,这节课基本上告一段落了,我们对分数又有了新的了解。 其实还存在好多问题,比如,有同学说5 个磁扣到底怎么回事?因为难度确实太大,我们以后再处理。
师:折腾了半天,我们要回想回想了,不然就白折腾了。这一大黑板结论都是我们共同努力的成果,你觉得哪个对自己的启发最大,你就上去圈哪个。大家圈的不一定一样,因为每个人的收获不一样。
生1:(圈了圆纸片)因为我之前没想到它。
(二)回首课始,联系对倍数的理解。
师:还记得课始时说老师的年龄是你的4倍吗?假设你11 岁,(板书:11)老师的年龄是44岁,(板书:44)谁能讲一个关于的故事?
【赏析】原来比较大小的时候可以来回说:我比你多2 个,你比我少2 个。到了倍数的时候,只说一个方面,即只说44 是11 的4 倍,学生会有困惑:倒过来说可以吗?张老师在这里适时将分数与倍数联系起来,让学生明白分数其实刻画的也是两个量之间的关系。
在这节“分数的再认识(一)”中,作为“分数意义”教学序列的第一节课,在课堂上,张老师通过想一想、画一画等手段,使学生认识到,“部分与整体的关系”不再只是数量上的比,还可以看作份数的比,帮助学生完成从“数量关系”到“份数关系”的转变。此外,这节课还强调在分数中部分与整体的互推,重视丰富对数概念的理解,注意发展学生对分数意义的深入理解。

