H型垂直轴风力机变桨机理研究进展

张立军，马东辰，胡阔亮，米玉霞，朱怀宝，顾嘉伟，刘静，严强

(1.中国石油大学（华东）机电工程学院，山东青岛，266580；2.上海麟风风能科技有限公司，上海，201508)

由于能源危机的日益严重，人们越来越倾向于对可再生能源进行研究。其中，风能以其绿色、无污染、可再生等特点已受到广泛关注。我国风能资源丰富，根据国家气象局的资料，近海70 m高度的年平均风功率密度可达300 W/m²以上，其中台湾海峡和东海南部风能资源甚为丰富，风速大于6 m/s 时的累计小时数可达5 000 h[1]。目前对风能利用的主要形式为风力发电。根据其风轮旋转轴相对地面的安装角度可以分为垂直轴风力发电机(VAWT)和水平轴风力发电机(HAWT)，与水平轴风力机相比，垂直轴风力机有无需对风装置、易于安装且便于维修等优点，尤其对于H 型垂直轴风力机来说，其叶片采用等截面结构，更适用于采用计算流体力学方法得到更精确的结论；同时，H型垂直轴风力机噪声小，比水平轴风力机拥有更广的应用范围，具有更高的商业使用价值。然而，现有的商业化H 型垂直轴风力发电机的风能利用率仅在30%～35%之间，远未达到其理论最大风能利用率64%[2]，且存在自启动能力弱等不足，在很大程度上限制了其规模化应用。为解决垂直轴风力机的低风能利用率问题，人们研究了多种提高其性能的方法，这些方法主要归纳为3种：一是风力机的结构优化，包括叶片翼型和主轴结构优化、叶片倾角改变、升阻互补等；二是翼型区域流场控制，例如利用导流片产生干扰气流，加装叶顶端板、襟翼、圆台型聚风罩等；三是叶片攻角改变，即通过改变叶片桨距角来实现对攻角的改变。其中，改变叶片桨距角以其调节方式简便、高效、直接等优点逐步受到人们的青睐。

1 变桨技术原理

现有的垂直轴风力机旋转过程中，叶片攻角随方位角不断变化，没有维持在最佳攻角处，是其风能利用率低的重要原因[3]。在桨距角调节过程中，主要角度是桨距角、攻角和方位角，这3个角度之间的关系如图1所示。图1中，W为诱导速度v和切向速度Rω的合成风速，ω为风轮的旋转角速度；θ为叶片方位角，当方位角θ位于0°～180°时，该区域称为风轮的上风区；当θ位于180°～360°时，称为风轮的下风区；α为叶片攻角，是合成风速方向与叶片弦线方向之间的夹角；β为叶片桨距角，是切向速度方向与叶片弦线方向之间的夹角。分析图1中的速度关系，可以得出垂直轴风力机叶片攻角的表达式为

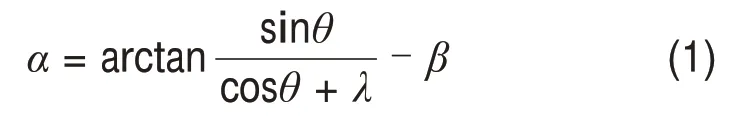
式中：λ为风轮的叶尖速比，

图1 翼型角度关系图Fig.1 Airfoil angle diagram

变桨技术的主要思路是通过调节桨距角使叶片攻角始终在重点旋转区域内处于最佳攻角处，即在一定叶尖速比下切向力系数达到最大时所对应的攻角，切向力系数与攻角的关系如图2所示。图2中，CL和CD分别代表翼型的升力系数和阻力系数，其值可由NACA 系列翼型空气动力学特性数据库查得。CT为切向力系数，是CL和CD在弦长方向的合成值。由图2中的几何关系，得到CT的计算式为

图2 叶片翼型气动力系数Fig.2 Aerodynamic coefficient of blade profile

随着风轮的旋转，叶片的合成风速方向时刻变化，攻角也随之变化，不易直接进行调节，而桨距角可通过调节叶片与旋转切向方向之间的夹角来调节。同时，由于桨距角与攻角之间有关，桨距角的改变也会使攻角发生变化，因此，变桨技术的核心是通过合理调节桨距角来间接控制对应攻角的变化，以实现对风力机气动性能的改善。

2 变桨规律研究

垂直轴风力机变桨距的研究重点在于变桨规律的可行性分析，目前国内外学者运用的主要研究方法有动量模型法、数值计算法和测试试验法等。

2.1 动量模型法

动量模型法利用流体力学(含空气动力学)的相关理论如动量理论、叶素理论、流管理论，借助水平轴风力机的分析方法，通过提出假定，建立模型的方法来计算。随着垂直轴风力机气动特性研究及空气动力学的不断完善，上述理论在风力机的设计和结构改进过程中起到了越来越重要的作用。其中，对于变桨距垂直轴风力机的理论研究，大部分学者运用的主要是叶素理论和双制动盘多流管理论。

2.1.1 基于叶素理论分析

垂直轴风力机在不同叶尖速比下运行时，叶片攻角的变化范围不同。应用叶素理论便于得到翼型在不同叶尖速比下的攻角变化范围，因此，在研究特定叶尖速比下风力机变桨规律时，通常选用叶素理论来进行分析。

顾华朋等[4]基于叶素理论，得到了NACA0012翼型在不同叶尖速比下攻角随方位角的变化关系，如图3所示。通过进一步结合翼型的升阻力系数随攻角变化关系，提出了一种以叶尖速比为分区的变桨方案，翼型的升阻力系数曲线如图4所示，其变桨方案如式(4)所示。该变桨规律的合理性主要在于：在低叶尖速比、大攻角工况下，通过调节桨距角使叶片攻角在60°～140°之间，此时垂直轴风力机主要靠叶片的阻力做功获得较大启动力矩；在较高叶尖速比下，叶片攻角变化范围较大，利用变桨方法控制叶片攻角在失速点±15°附近，使得叶片可以依靠升力做功从而获得较大且稳定的扭矩。通过建立风轮扭矩系数模型，分析了该变桨运行规律的有效性。

吴祥辉等[5]基于叶素理论，进一步对叶尖速比λ<1.0 情况下的变桨规律进行了讨论，主要是通过求解不同的方位角和桨距角时所对应的扭矩力，比较了各个方位角下最大扭矩力对应的最佳桨距角，进而得到1周桨距角的调节规律。得到的桨距角变化规律如图5所示。

图3 定桨叶片攻角变化曲线[4]Fig.3 Change curve of attack angle with fixed pitch angle[4]

图4 NACA0012翼型大攻角升阻力系数曲线[4]Fig.4 NACA0012 airfoil lift drag coefficient curve of high attack angle[4]

2.1.2 基于双制动盘多流管理论分析

与叶素理论不同，双制动盘多流管理论不仅以单一叶片为分析对象，它还将风轮旋转分为上下风区，并将转子作用盘面沿垂直于来流的方向细分成多个独立微流管[6]，理论上看对于垂直轴风力机的气动性能分析更为合理。

图5 桨距角变化规律[5]Fig.5 Changing rule of pitch angle[5]

PARASCHIVOIU 等[7]针对一种7 kW 的垂直轴风力机，将CARDAAV 代码与基于遗传算法的优化器相结合，开发了一种新的优化工具来定义叶片桨距角的变化。以基于双制动盘多流管理论求解的气动参数为评价指标，验证了优化算法的可行性。

张立勋等[8]针对变桨距垂直轴风力机凭某一尖速比下最优变桨规律无法启动和变桨规律中的不连续性问题，重点对此不连续部分进行了修正，如图6所示，通过人工设计一条斜率最小的直线段，连接变桨规律中不连续段的两端，并修改方位角n×180°附近的叶片桨距角为90°，实现规律连续性。采用双制动盘多流管理论对所设计的变桨规律进行力矩特性分析，结果显示，采用该变桨规律的风力机能够可靠自启动且高效发电。

张立军[9]针对垂直轴风力机下风区风况的复杂性，提出了局部叶尖速比的概念，基于双制动盘多流管理论，重新建立了下风区叶片攻角与桨距角之间的关系式，对双制动盘多流管理论进行了改进和完善。

综合上述研究发现，采用动量模型法对变桨距垂直轴风力机进行研究的目的主要有2个：一是通过建立理论模型，得到桨距角调节规律；二是以风力机的风能利用率为评价指标，判定变桨前后风力机的性能变化，验证变桨规律的可行性。这种研究方法简单易行，可以直接反映风力机的出力效果，便于对比变桨前后风力机的气动性能，但不能直观观察风力机流场的变化，对于功率系数变化的原因也缺少探讨。

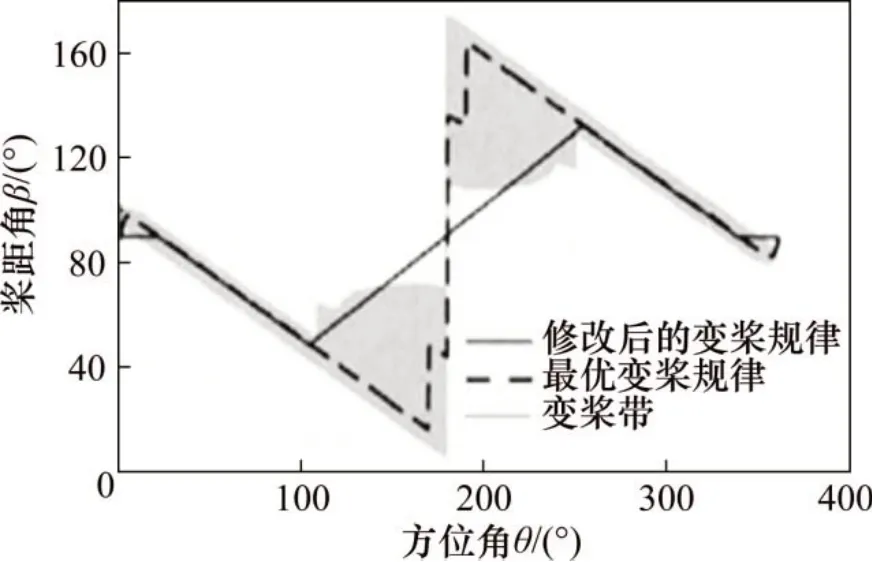
图6 修正前后变桨方案对比[8]Fig.6 Schemes comparison of before-and-after variable pitch modification[8]

2.2 数值计算法

近几年来，随着计算流体力学(CFD)技术的快速发展，数值计算方法以其精度高、计算速度快、成本低等优点，成为垂直轴风力机研究的主要手段之一[10]。对变桨距垂直轴风力机的研究通常采用二维计算方法，主要原因在于变桨技术并未改变翼型形状，研究重点是变桨前后风力机气动性能参数的改变，相对于三维计算，二维计算网格设置相对简单，工作量小，计算效率高[11]。一种经典的垂直轴风力机二维仿真模型如图7所示，图中d为风轮直径。

针对垂直轴风力机的变桨问题，数值计算法的一个重要优势在于通过改变边界条件，便于研究不同桨距角下风力机的气动性能差异，模拟不同叶尖速比下风力机所处工况条件。张立勋等[12]仿真研究了不同桨距角下风力机的气动性能，通过分析不同桨距角下力矩系数，如图8所示，提出一种主动式变桨规律：设置内偏置桨距角或小幅值外偏置桨距角，使风力机在小方位角下进入有效力矩作用区；设置外偏置桨距角使风力机延缓退出有效力矩作用区。研究表明，这种方法增加了有效切向力的作用范围。

对于同一类问题，ABDALRAHMAN等[13]利用FLUENT 流体仿真软件对不同叶尖速比下桨距角进行研究，通过分析同一叶尖速比下桨距角在不同方位角下的出力情况，得到了风轮旋转1 周时，各个叶片对应的桨距角变化规律，如图9所示。

图7 垂直轴风力机二维仿真示意图Fig.7 Two-dimensional simulation diagram of VAWT

图8 不同桨距角下力矩系数图[12]Fig.8 Torque coefficients at different pitch angles[12]

除此之外，数值计算法在观察流场分布上有其独特优势。垂直轴风力机风能利用率较低的重要原因在于攻角的不断变化，而攻角改变所导致的叶片周围流场的变化是翼型升阻力系数变化的根本原因。借助CFD 仿真软件，能够直观观察叶片在各个方位角下的流场情况，对于研究变桨式风力机有较好的辅助作用。左薇等[14]采用笛卡儿动网格数值计算方法研究了动态变桨式H 型风力机的气动特性，重点分析了变桨前后不同时刻叶片周围的涡量云图，研究发现动态变桨方式不会生成前缘分离涡，且可以避免叶片脱落尺度较大、强度较强的尾缘分离涡。

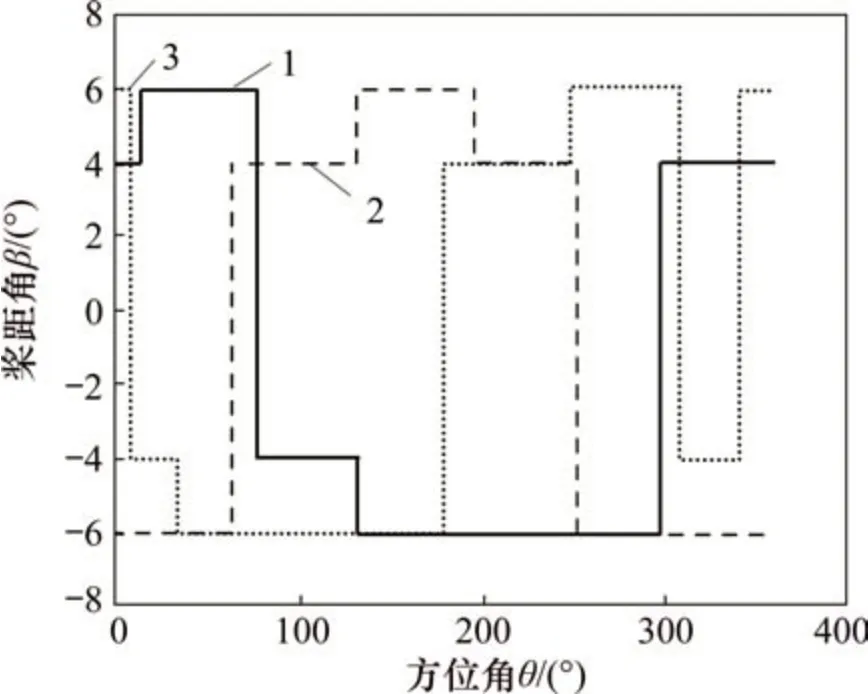
图9 桨距角变化图(叶尖速比λ=1.0)[13]Fig.9 Pitch angle variation diagram(tip speed ratioλ=1.0)[13]

彭伟等[15]提出一种新型随动变桨距垂直轴风力机结构，如图10所示，这种风力机的主要特点在于：当叶片处于迎风面时，叶片始终与来流风垂直；当叶片处于背风面时，叶片始终与来流风平行，以此来减少阻力，增加其产生的力矩。通过对该变桨距风力机进行CFD压力场仿真分析可知，该风力机在转动过程中可以使叶片产生的压力相对稳定，有助于风力机保持匀速转动。

图10 新型随动变桨垂直轴风力机示意图[15]Fig.10 Schematic diagram of a new type of follow drive variable pitch vertical axis wind turbine[15]

REZAEIHA 等[16]指出，当前对风力机变桨规律的研究局限在于以稳态值(如风能利用系数等)为指标，而忽视了对瞬态值(如风力机旋转过程中的实时负载及力矩变化、边界层分离现象及层流与湍流的转化情况等)的研究。为此，通过建立风轮CFD 仿真模型，对不同桨距角下风力机的扭矩系数、叶片压力分布、旋涡脱落等情况进行了研究，综合考虑瞬态值与稳态值的变化，给出了最佳桨距角为β=-2°。其中，扭矩系数的变化趋势如图11所示[16]。

图11 不同桨距角下风力机扭矩系数图[16]Fig.11 Torque coefficient diagram of wind turbine at different pitch angles[16]

上述研究均采用数值计算法，充分发挥了数值计算法精确度高、对仿真结果后处理能力强、流程显示直观等优点。可以预见的是，随着计算机算法的不断完善，CFD 仿真计算的可靠性将越来越高，会为学者们的研究带来更大便利。

2.3 测试试验法

数值计算法虽然便于求得风力机的气动参数，且易于观察风力机周围流场的变化，但是由于所选计算模型、条件设置以及网格质量等因素，计算仍存在一定的误差，而测试试验法则更加直观，并且试验得到的数据也更具有说服力。

目前，测试试验法主要分为2种。

一种是将风力机样机置于实际风场中，直接利用传感器等测试仪器和设备监测风力机的性能。例如LEE等[17]为验证基于数值计算得到的摆线式变桨规律[18]的正确性，搭建了风力机装置并进行野外试验，同时利用LabVIEW 软件平台对风力机实时功率进行采集，结果如图12所示[17]，对比发现试验结果低于CFD 仿真结果，但2 种结果的趋势大致相同。这种研究方法的优点在于风力机位于实际流场中，对工况的还原度高，但存在的主要缺点是不能人为地改变风速，对自然环境的依赖程度较强。同时，由于需要搭建实际的风力机测试系统，研发成本较高，而且基于风速的随机性，受地势、周围环境等因素的影响，有时候测试结果未必真实反映风力机的性能。

图12 试验结果与仿真结果的对比[17]Fig.12 Comparison of experimental results and simulation results[17]

另一种测试试验方法是对变桨距风力机在风洞内进行性能测试，如图13所示，通过调节轴流风机的转动频率，可以实现对风速可控调节，监测不同工况下风力机的性能[19]。但这种方法需要制造标准化的风洞，研发成本也比较高。

图13 垂直轴风力机风洞试验系统[19]Fig.13 Wind tunnel experimental system for VAWT[19]

张立军等[20]研发了一种小型变桨距垂直轴风力机样机，如图14所示，利用自制风洞，模拟了垂直轴风力机的流场情况，对3～10 m/s 风速下的风力机的发电功率进行了监测，试验结果如表1所示，结果显示，变桨距风力机的发电效率较定桨距风力机的至少能提高7.86%。

在变桨规律研究中，测试试验法的主要优势是可信度大，但也存在制造成本高、研究周期长、占地面积大等不足，成为阻碍其发展的主要原因。但随着新能源技术越来越受到重视、国家政策的支持及相关产业链的完善，变桨距垂直轴风力机的测试试验也将迎来更好的发展机遇。

图14 变桨距垂直轴风力机[20]Fig.14 Variable pitch vertical axis wind turbine[20]

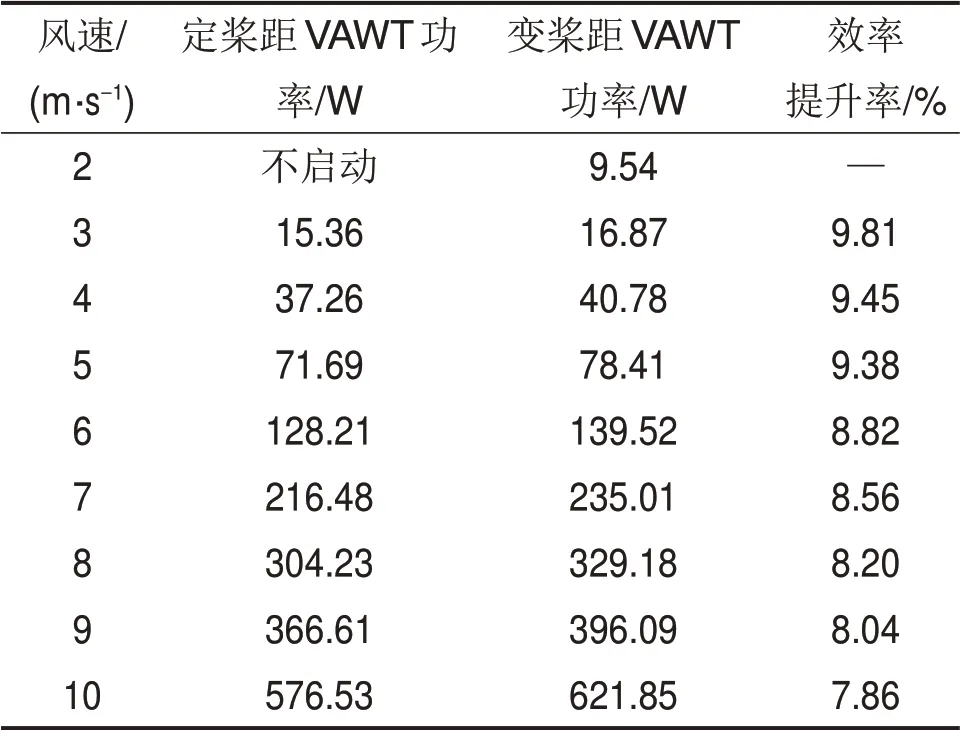
表1 2种风力机发电功率的对比Table 1 Comparison of power generated by two types of wind turbines

3 变桨实现方法探讨

对于变桨距垂直轴风力机而言，无论是采用动量模型，还是采用数值计算以及测试试验，最终目的在于实现其商业化应用。而变桨距风力机制作的关键在于使其叶片桨距角的变化与所求得的变桨规律相一致，为此，国内外学者对此也进行了相关探索和研究，目前实现变桨的方法主要分为2 种：一是机械传动变桨，二是液压传动变桨。

3.1 机械传动变桨

采用机械传动机构是实现叶片桨距角调节的有效途径。2014年，杨凯等[21]利用伺服电机的精确性和蜗轮蜗杆减速机的自锁功能，设计了一种自主变桨式风力机，如图15所示。其主要工作原理是：利用光电编码器检测风力机的转速及叶片位置，通过变桨伺服电机调节叶片桨距角，并利用蜗轮蜗杆减速机的反向自锁功能，保持桨距角在特定区域内保持不变。

图15 变桨风力机剖面图[21]Fig.15 Cross view of pitching wind turbine[21]

上述方案的局限性之一在于蜗轮蜗杆价格较为昂贵，制作成本较高。近几年，许多学者提出了利用连杆机构实现对桨距角的调节。YAMADA等[22]提出采用四连杆机构来控制风力机桨距角的垂直轴风力机模型。JAIN 等[23]也提出类似的四连杆机构模型，如图16所示。

图16 连杆式变桨距风力机模型[23]Fig.16 Model of variable pitch VAWT with connecting rod[23]

廉正光等[24-25]提出一种采用双曲柄调距机构的垂直轴风力机，如图17所示，该风力机主要采用双曲柄调距机构及双偏心轴机构。

图17 基于调距机构的整体风机模型[24]Fig.17 Overall structure of distance adjusting mechanism[24]

对于垂直轴风力机变桨机构中连杆机构的设计重点在于各段杆长的确定。张立军等[20]采用随机方向法对一种双曲柄机构进行优化设计，确定了各杆的杆长，得到了不同叶尖速比下变桨机构的参数组合。双曲柄机构的几何分析如图18所示。

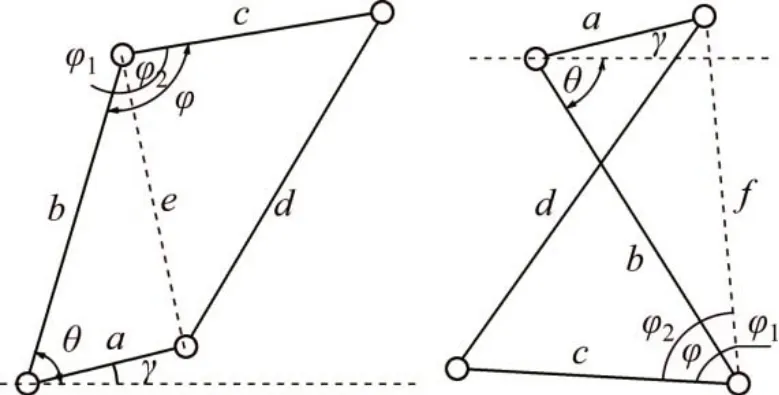
图18 双曲柄机构几何分析图[20]Fig.18 Analysis diagram of double crank mechanism[20]

采用机械传动方式实现周期性桨距角调整的优点在于结构紧凑、传动平稳、便于维护等，但是并不利于风力机的大型化发展。

3.2 液压传动变桨

针对兆瓦级H 型垂直轴风力机，变桨机构的设计需满足驱动力大、有足够的强度和精度等要求[26]，采用液压传动变桨系统，可以起到机构响应速度快、定位准确、驱动力大等优点。如图19所示，液压变桨系统主要由变桨控制器、D/A 转化器、电液比例阀和变桨执行机构等组成[27]。其工作原理是：通过电液比例阀控制液压缸活塞杆驱动曲柄连杆机构实现控制变桨机构的桨距角，通过位移传感器，将活塞杆的位移反馈给PID桨距控制器，PID桨距控制器根据桨距角的给定值和实际响应的测量值进行比较形成偏差，进而进行参数放大，计算出电液比例阀的控制电压。在此基础上，再通过D/A 转换器控制电液比例阀的输出流量，从而驱动液压缸活塞杆的运动，实现桨距角的大小调节[28]。

图19 液压变桨系统控制图[27]Fig.19 Control diagram of hydraulic pitching system[27]

除可用于变桨外，液压技术还可实现垂直轴风力机的稳压恒频发电。为了使垂直轴风力机吸收更多的风能，降低研发成本，张立军等[29-30]提出了一种塔架式多层多轴垂直轴风力机，其结构如图20所示。“多层”可以使风力机充分吸收不同高度上的风能；“多轴”可以降低风剪效应[31-32]对单一旋转轴的制约，减小其旋转轴在上下位置处的扭矩差。同时，该风力机采用液压传动，不但省去了机械式变速箱和整流逆变器，并用普通交流电动机代替了永磁发电机，制造成本降低了约30%，而且占地面积小；采用补偿+稳能技术，系统能输出(50±0.2) Hz 的恒频率的交流电。目前该风力发电机正处于初试阶段，初步测试结果表明，基本能够满足并网要求。

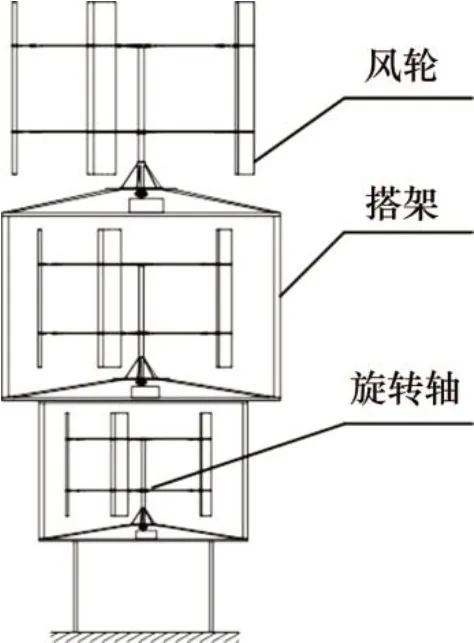
图20 多层多轴塔架式垂直轴风力机[30]Fig.20 VAWT with multi-layer multi-axis tower[30]

4 变桨机构实现的难点剖析

现阶段，虽然各国学者对于变桨距H 型垂直轴风力机做了大量研究，且对于变桨规律的实现也提出了多种设计方案[33-35]。但目前除了用于风速高于切出风速时的“限速”外，垂直轴风力机用于1周连续改变攻角进而提高风能利用率的变桨机构并未得到商业化应用，究其原因主要是在变桨机构响应时间、1周实时变桨规律计算、下风区流场复杂性分析和动态失速下可靠变桨等方面存在理论和技术瓶颈，机构实现起来非常困难，尤其是对中小型垂直轴风力机。

4.1 变桨机构响应时间

图21 变桨系统控制流程图Fig.21 Control flow chart of variable pitch system

目前的变桨系统控制流程图如图21所示，变桨结构复杂，主要包括感应机构、调节机构、机械与执行机构等多个环节，而且存在闭环控制，很难实现机构的快速响应。特别是对于中小型垂直轴风力机而言，风力机的额定转速高，对应叶片攻角的变化频率较快。以上海麟风风能科技有限公司所生产的小型垂直轴风力机为例，风力机的相关参数如表2所示。由表2可知：这些小型风力机方位角的变化频率较高，如额定功率为3 kW的风力机，在额定风速和额定转速下，方位角每变化10°，仅需要0.015 s[36]。由于风速的随机变化、叶片的惯性、连接机构间的间隙、外部环境等因素的影响都会限制整个变桨机构在实际运行中的反应速度，因此，变桨系统很难在较短时间内适应快速的风速变化而完成叶片攻角的改变。

表2 小型垂直轴风力机相关参数Table 2 Related parameters of small vertical axis wind turbine

4.2 1周实时变桨规律

在额定工况下，上述麟风3 kW 垂直轴风力机的叶尖速比λ=0.86，在该叶尖速比下，叶片攻角的1 周变化规律如图22所示。由图22可知：当方位角变化10°时，在大部分方位角下攻角变化5°左右，且在方位角θ=180°附近，攻角发生跳变。因此，在极短时间内，叶片攻角变化范围较大。

而在实际工作状态下，通常来流风的风速和风向都在实时变化。风速的改变带来风力机叶尖速比的变化，而在不同叶尖速比下，风力机的攻角变化规律和桨距角调节规律不同；风向的改变带来叶片所处方位角的变化，而1周变桨规律强调在每个方位角处，叶片都对应1个桨距角理论调节值，在这个理论调节值下对应最佳攻角。因此，在实际工况下，为维持风力机较高的输出功率，每个时刻对叶片转动角度的调节值都不尽相同。而如何快速识别风速随机变化，确定叶片实时所处方位角，然后再计算桨距角调节值，已成为变桨机构实现的难点。

4.3 下风区流场计算复杂性

图22 叶尖速比λ=0.86时攻角变化规律Fig.22 Rule of attack angle with blade tip velocity ratioλ=0.86

与水平轴风力机相比，垂直轴风力机流场结构更复杂，属于典型的大分离非定常流动，且叶片在上风区和下风区要2次受到来流风的作用。当气流经过上风区叶片到达下风区时，出现了扰流现象，此时下风区各个方位诱导速度发生了改变，且方向也与来流风方向不同。由于下风区流场分布复杂，双致动盘多流管理论已经很难完全反映诱导速度方向的变化，故在对垂直轴风力机1周变桨规律制定时，下风区桨距角调节规律很难准确得到。而目前关于垂直轴风力机的分析，大都假设了垂直轴风轮下风区各个方位的诱导速度方向不变，这样的假设虽简化了计算，但研究结果不能完全真实反映实际情况。

本文作者将动量模型和数值计算技术相结合，在下风区提出了局部叶尖速比的概念，并重新建立了下风区叶片攻角的计算模型[9]，如图23所示。

定义下风区局部叶尖速比X’为

图23 下风区叶片攻角分析模型Fig.23 Blade angle of attack analysis model in downwind area

根据图23所示的几何关系，得到下风区叶片攻角的计算公式为

利用数值计算对推导出的垂直轴风轮下风区攻角的计算公式进行了验证，在此基础上制定了下风区攻角调节策略。需要指出的是，这种方法是本文作者的一种合理尝试，由于下风区流场的复杂性，目前关于下风区桨距角调节策略的研究还尚不成熟，或许需要进一步建立针对下风区流场精确计算的新方法。

4.4 动态失速下实时变桨控制规律

4.4.1 风力机运行中动态失速现象的发生情况

动态失速是指在进口来流攻角快速变化的过程中，风轮叶片所表现出的与静态风洞实验完全不同的气动特性[37]，是垂直轴风力发电机低尖速比下运行时的必然结果[38]。NACA0012翼型在动态失速下上下风区的失速攻角为17°和-17°[39]。图24所示为在叶尖速比为0.5，1.0 和2.0 时该翼型攻角随方位角的变化趋势以及在这些叶尖速比下风力机旋转1周时失速区的位置和大小。可见叶片主要工作在失速区，且叶尖速比越低，失速区越大，这与相关研究结论是一致的[37]。由图24可知：λ=0.5时失速区占1周方位角的比例约为80%，此时叶片周围出现分离流场，受到的气动阻力急剧上升，攻角调节更加复杂。另外，现有的叶片动态气动性能相关实验数据较少，这也极大地制约了垂直轴风力机变桨规律的突破性研究。

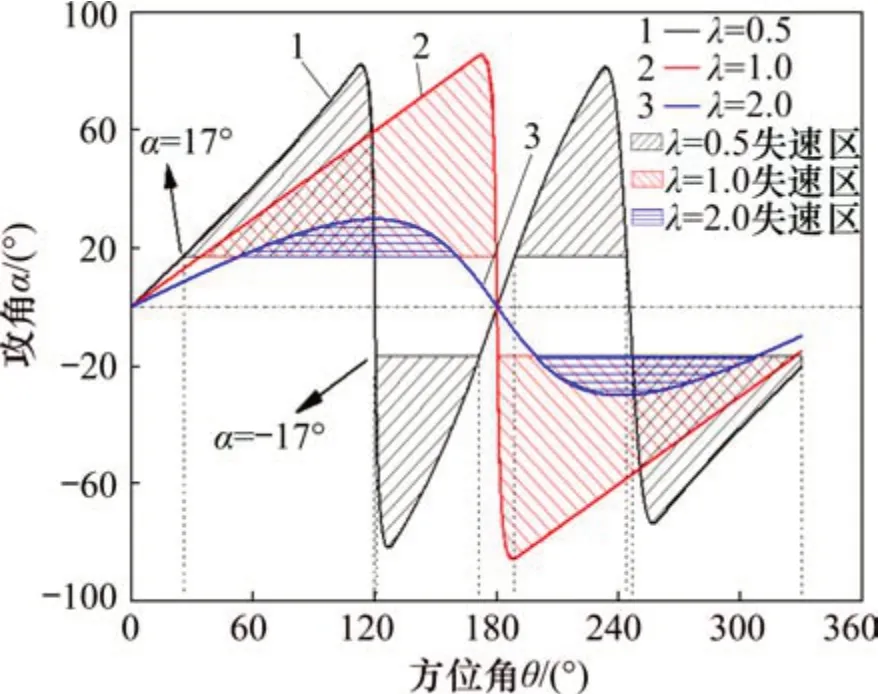
图24 3种叶尖速比下叶片攻角变化规律及失速区Fig.24 Variation of blade angle of attack and stall zone under three tip velocity ratios

4.4.2 考虑动态失速下实时变桨规律

本文作者基于美国Sandia 国家实验室动态失速下测得的风力机实验数据与风洞静态实验结果[40-41]，以获得风轮的最大切向力为目标，得到了垂直轴风力机在上风区和下风区的最佳理论攻角。理论上，当风力机以最佳攻角运行时，将不再有动态失速的现象产生。基于双致动盘多流管理论进行Matlab编程计算，给出了垂直轴风力机1周变桨距规律，变桨前后风轮切向力对比如图25所示。从图25可知：利用该变桨距规律得到的风能利用率可以由34.6%提高到42.8%。这说明这种变桨距规律能够较好地提高垂直轴风力机的切向力，进而增加风轮的转矩[39]。

图25 变桨前后风轮所受切向力对比Fig.25 Contrast of tangential force before and after pitch angle adjustment

5 未来发展

近几年关于变桨距垂直轴风力机的研究发展迅速，随着流体理论的完善、计算流体技术的进步和实验经验的积累，垂直轴风力机变桨技术将会越来越成熟。未来几年，“大型化、高效率、低成本”仍将是垂直轴风力机发展的主要趋势，尽管大型化垂直轴风力机由于高度较高，所受风剪效应的影响较大[42-44]，主轴偏振剧烈[45]，但是其转速下降，对变桨调节机构的响应时间可能要求变低，因此，新的流场模型的建立和空气动力学理论的提出，更准确合理的桨距角调节规律和更可靠经济的变桨机构以及智能控制系统的研发，都将成为未来变桨距垂直轴风力机的研究热点和难点。

同时，未来风电发展也将会是大数据、人工智能、物联网等新技术的时代，数据是一种潜力巨大、影响深远的能源，为尽快地利用这种能源，一些风能公司创建了大数据监控平台，利用多种传感器融合技术，广泛采集机组运行数据，建立运行数据库和风资源数据库，预先感知运行状态，为机组长期稳定高效运行和优化升级提供理论支撑。该技术在H 型变桨式垂直轴风力机上应用的可行性在于：通过大数据平台的创建，可以快速根据来流风风速及风向预先感知风力机的流场情况，从而得到桨距角的调节值，调动变桨机构提前响应，以弥补响应时间的迟滞性。

此外，为提高垂直轴风力机风能利用效率，除设计单一变桨机构外，各国学者还致力于研究基于新材料的翼型智能柔性变形技术[46]、风轮外围大区域流场实时控制[47]及采用辅助设备[48]向高空收集高风能等新思想，基于新材料和信息技术，探索开发智能风力机，这些途径都将为垂直轴风力机的商业化应用起到一定的推动作用。

6 结论

1)变桨技术的核心在于通过调节桨距角以使攻角维持在最佳角度，从而获得较高的翼型升阻比以提高风力机性能。目前对于垂直轴风力机变桨规律的研究方法主要包括动量模型法、数值计算法和测试试验法等，其中，数值计算法是H 型垂直轴风力机变桨技术研究的主流方法。

2)无论是采用机械传动变桨，还是液压传动变桨，局部方位角变桨或全方位角变桨未能应用于工程实际中的主要难点在于：变桨控制系统的复杂性导致系统整体响应时间较长，无法适应风速风向的快速随机变化；叶片攻角的不断改变、方位角位置变化，以及实际工况下叶尖速比的波动，使得1周变桨规律实现很困难；叶片在上风区和下风区2次扫掠来流风，导致下风区的诱导速度分布很复杂，给下风区变桨规律的理论计算带来了技术瓶颈；动态失速下实时变桨控制规律的研究更复杂，目前仅限于理论研究，且受限于动态气动性能相关实验数据的缺乏。

3)目前，商业化小型H 型垂直轴风力机的风能利用率为30%～35%，随着变桨技术从原有的仅限于“限速”作用，逐渐地向局部方位角变桨，再到全方位角变桨方向演变，风能利用率也将逐步提高。同时，随着人工智能、大数据、物联网等新一代信息技术的发展，风场外围大区域的风速、风向等参数将会被提前预知；智能柔性变形机翼技术、智能材料与结构和新型传感控制技术的快速发展，将催生智能风力机的诞生。基于这些技术的融合，未来全方位角变桨技术真正应用于大型垂直轴风力机的可能性将会更大。