140 km/h高速地铁隧道净空断面面积研究

冉腾飞，梁习锋，熊小慧

(1.中国铁路北京局集团有限公司北京动车段，北京，102600；2.中南大学交通运输工程学院轨道交通安全教育部重点实验室，湖南长沙，410075；3.中南大学轨道交通安全关键技术国际合作联合实验室，湖南长沙，410075；4.中南大学轨道交通列车安全保障技术国家地方联合工程研究中心，湖南长沙，410075)

隧道内压力波动幅值与列车运行速度的平方近似呈线性关系[1]，因此，高速地铁列车运行速度的提高会引起隧道内压力变化更加剧烈，并且当地铁列车经过隧道洞口及中间风井等截面突变处时，隧道内压力会发生剧烈变化；当剧烈的压力波动传入车内时，会引起乘客耳膜压痛甚至呕吐，产生乘坐不舒适等问题[2]，因此，有必要对高速地铁列车在隧道中运行时的压力舒适性问题进行研究。国内外学者主要采用数值计算的方法研究地铁隧道空气动力学问题，如：李志伟等[3]利用高速铁路隧道空气动力学的研究方法，分析了竖井位置、数量、截面积等参数对列车表面压力的影响，但没有考虑列车站间运行对隧道内压力的影响，也没有考虑地铁隧道结构的特殊性；王秀珍[4]采用三维数值模拟方法研究了车速、隧道截面形状、隧道长度等因素对地铁列车气动效应的影响，但没有考虑隧道断面面积对隧道内压力的影响，也没有考虑车内压力舒适性的问题；刘俊等[5]分析了不同速度的地铁列车通过不同隧道时的空气动力学效应，得到了不同密封指数下地铁列车所需的最优隧道断面面积，但没有考虑中间风井对隧道内气动效应的影响；刘伊江[6]计算了不同车速、不同隧道断面下的压力波及压力变化梯度，但其计算模型完全参考了高速铁路隧道空气动力学的研究方法，未充分考虑地铁隧道网络的复杂性；NIU等[7]分析了地铁列车在隧道中的站间运行情况，但忽略了中间风井对隧道内气动效应的影响。与铁路隧道相比，地铁隧道的隧道截面积较小，地下段长度很大[8]，而且隧道内有中间风井等通风设施，这些构造会导致隧道内压力发生剧烈变化。地铁列车在运行过程中，需要频繁地在车站间启动加速与制动停车，在地下线路与高架线路间进行转换，为此，本文依托下一代高速地铁项目，通过对时速140 km/h 高速地铁列车在隧道中运行时的气动效应进行数值计算，得到高速地铁隧道净空断面面积与列车密封指数的匹配关系。本文结合地铁隧道结构的复杂性、特殊性以及地铁列车的行车特点，对高速地铁隧道内的压力变化及地铁列车车内压力变化进行研究。首先，利用动模型试验验证本文数值计算方法的正确性与可信度；然后，计算列车由明线驶入隧道与站间运行这2种运行工况下车体表面的压力变化情况，确定哪种运行工况更危险；最后，计算在这种更危险运行工况下隧道净空断面面积与列车密封指数的匹配关系。

1 计算条件

1.1 数学模型

地铁列车在隧道中运行时，隧道内空气受到隧道壁面和车体表面的限制无法自由流动，并且空气会受到隧道壁面和车体表面的强烈挤压，因此，需要将隧道内的空气视为可压的理想气体。列车周围流场的雷诺数Re约为106，基本上为湍流流动，因此，本文采用κ-ε湍流模型[9]对隧道内的空气进行湍流模拟。

文中数值计算软件采用Fluent，采用SIMPLEC 算法耦合求解压力与速度；对流项采用高阶精度的SECOND 格式离散，扩散项采用二阶中心格式离散。在离散过程中，时间项采用二阶隐式格式。

1.2 计算模型、计算域及边界条件

图1所示为数值计算采用6车编组的A 型地铁列车，对地铁列车外形进行了简化，忽略了转向架、受电弓等的影响[9-11]。其中，列车高H=3.8 m，宽W=3 m，整车长Ltr=139.5 m，列车横截面面积Av=9.785 m2。地铁列车表面从头车到尾车共布置6个测点，测点布置情况如图1所示。

图2所示为数值计算采用的隧道断面计算模型。由图2可见：数值计算采用隧道的盾构直径D分别为6.0，6.6，7.0 和7.6 m，对应的净空断面面积At分别为26，32，35 和42 m2，对应的阻塞比β(即列车横截面积与隧道净空断面面积的比值)分别为0.376，0.306，0.280 和0.233。其中D=6 m 与At=26 m2分别为现有120 km/h速度等级地铁隧道的盾构直径与净空断面面积。

图1 A型地铁列车计算模型Fig.1 Computational model of A-type subway train

图2 隧道断面计算模型Fig.2 Computational model of tunnel cross section

在CFD 计算中，网格质量会影响数值计算结果的效率与精度，因此，本文采用ICEM CFD 软件对隧道中的流体区域进行结构网格划分：采用外C网格与O网格将列车壁面、隧道壁面和相应的BLOCK的surface进行映射，建立无厚度壁面；中间风井与隧道连接处的结构类似于T型管，可以划分为三通网格[12]，图3所示为部分网格的划分情况。

图3 计算网格分布示意图Fig.3 Schematic diagram of mesh distribution

采用滑移网格法模拟地铁列车在隧道中的运行，图4所示为所采用的计算区域。为了满足地铁隧道通风换气、环控和消防等方面的要求，在较长的地铁隧道中均需设置中间风井，因此，本文在隧道运行区间的中间位置设置矩形截面的风井[7]。其中，风井壁面的长×宽×高为4 m×4 m×15 m，风井出口域的长×宽×高为50 m×50 m×15 m。

为了保证列车周围流场充分发展，在模拟地铁列车由明线驶入隧道的情况时，设置车头距离隧道入口50 m，车尾距离流域入口150 m，如图4(a)所示。

图4 计算区域Fig.4 Computational domains

为了避免隧道出口边界受尾流的影响，保证列车尾流在流场长度方向充分发展，避免出现流场阻塞效应[13]，沿隧道长度方向，在2 km 运行区间前后各添加长为1 km 的隧道，如图4所示；同时，将隧道出口(站间运行时为隧道入口和隧道出口)的边界条件设为压力远场(即无反射波返回)[11]。

列车运动边界条件如下：X方向速度分量为列车运行速度，Y和Z方向速度分量为0 m/s；流域侧面、顶面给定为对称面，流域底面、风井壁面、隧道壁面及地面均给定为无滑移壁面边界条件。同时，为了使流场得到充分发展，将中间风井压力出口边界静压设为pout=0 Pa；在列车驶入隧道的计算域中，将压力入口边界静压设为pin=0 Pa[9]。

2 数值算法验证

为验证数值计算结果的正确性与可信度，利用中南大学轨道交通安全教育部重点实验室自主研制1:20 缩比的动模型试验装置，对时速为100 km/h的地铁列车匀速通过盾构直径为6 m、长度为1 km 隧道时的场景进行动模型试验，并进行相同工况的数值计算验证。图5所示为动模型试验装置的列车和隧道模型，数值计算方法为可压、非定常N-S方程与κ-ε湍流方程[9]。

图5 动模型试验模型Fig.5 Model of moving model test

图6所示为动模型试验中的测点布置示意图。其中，隧道壁面上共布置6个测点，车体表面上共布置6个测点。

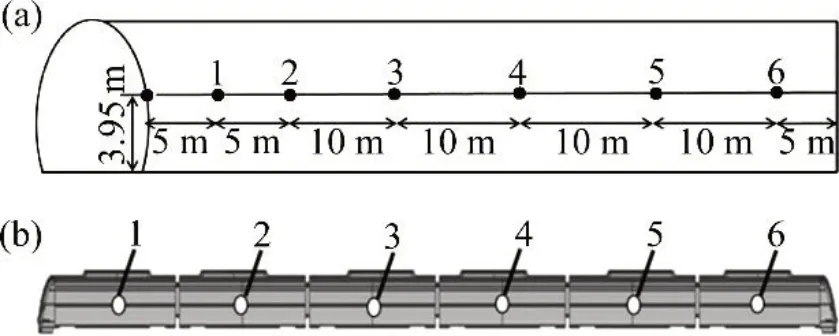
图6 动模型测点布置示意图Fig.6 Measurement points on model

图7所示为数值计算与动模型试验中车体表面2 号测点和隧道壁面3 号测点的压力对比波形；相应的测点压力变化的结果对比如表1所示。

图7 压力对比波形Fig.7 Comparison of pressure curves

由图7可见：这2种方法得到的测点压力曲线变化规律一致，仅最大值、最小值和峰峰值略有差异，最大相对误差为5.9%，在数值计算误差容许范围内，说明该数值计算方法能够较好地模拟地铁列车通过隧道时所引发的空气动力效应问题，从而验证了本文数值计算方法的正确性与可信度。

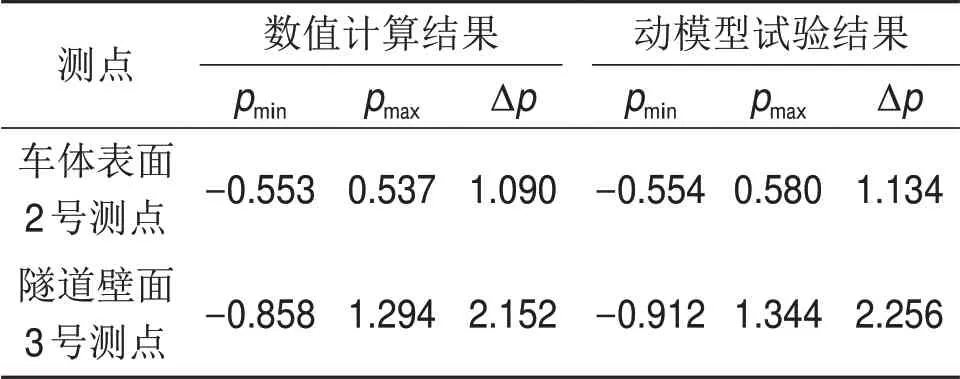
表1 压力变化结果对比Table 1 Comparison of pressure variations kPa

3 运行工况对隧道内气动效应影响

3.1 运行工况简介

在地铁列车的众多运行工况中，列车由明线驶入隧道和站间运行的工况为隧道内压力波动较为剧烈的情况。其中，不同运行工况下的列车运行速度如图8所示。

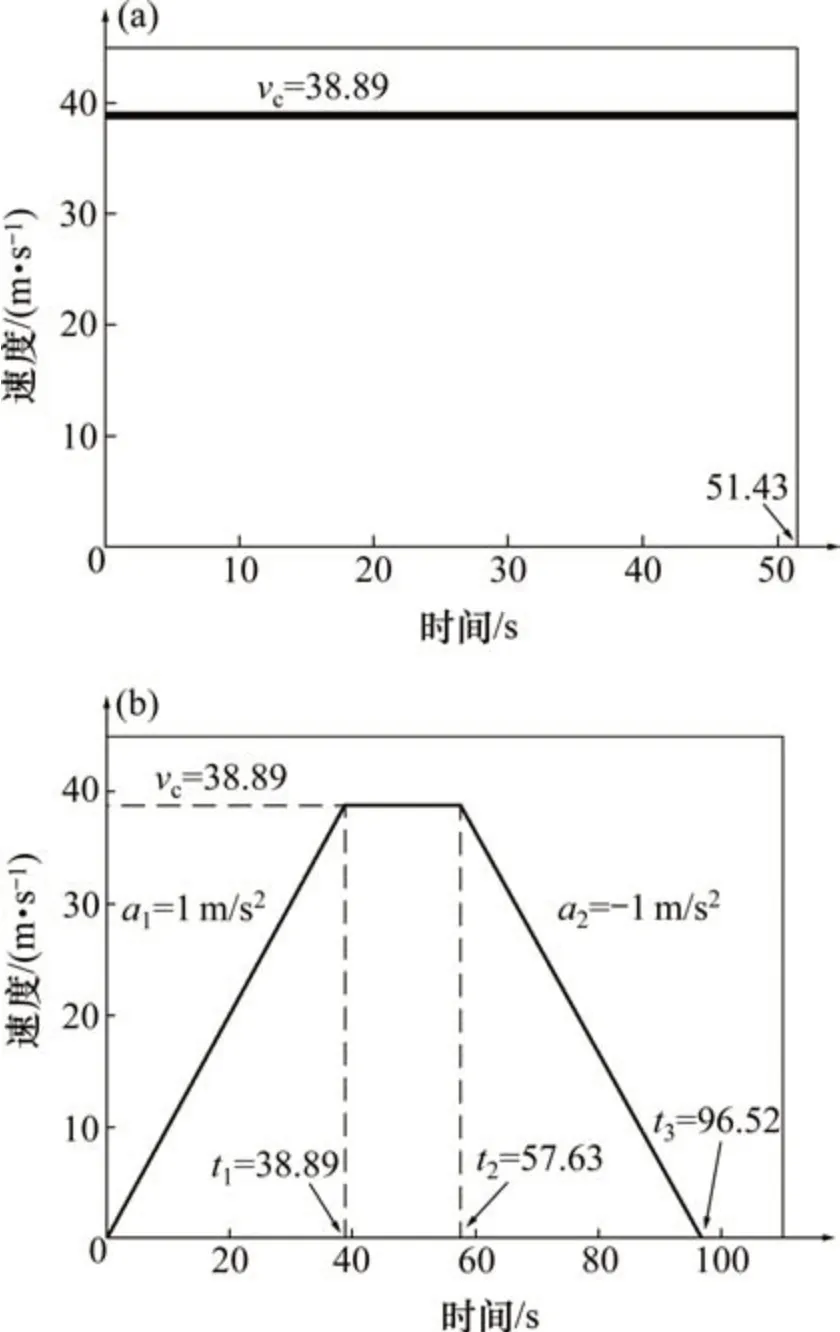
图8 列车运行速度图Fig.8 Running velocity diagrams of train

图8(a)中，列车以vc=38.89 m/s 的速度匀速运行51.43 s，因此，列车由明线驶入隧道过程中的运行区间长度为d1=vct=2 000 m；图8(b)中，为使数值模拟简单有效，将列车的站间运行看成匀加速、匀速与匀减速运行的过程[7]，其中列车以a1=1 m/s2的加速度匀加速运行至t1=38.89 s，再以vc=38.89 m/s 的速度匀速运行t2=51.43 s，最后以a2=-1 m/s2的加速度匀减速运行t3=90.32 s 停止运行。因此，地铁列车站间运行的区间长度为d2=

3.2 更加危险运行工况的确定

为了分析列车在不同工况下运行时隧道内的压力变化，确定更加危险的运行工况，对不同运行工况下高速地铁列车在断面面积At=26 m2的隧道中运行时的气动效应进行数值计算。其中，在不同运行工况下，车体表面1号测点的压力波对比如图9所示。

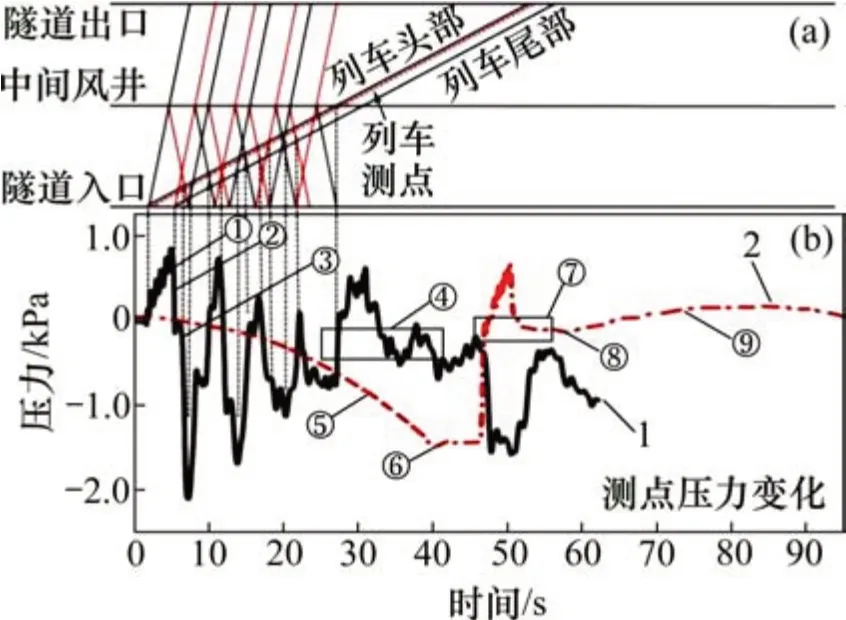
图9 不同运行工况下车体表面测点压力变化曲线Fig.9 Pressure curves of train surface’s measurement points with different operating conditions

从图9可以看出，不同运行方式对车体表面测点压力变化的影响很大。

当列车由明线驶入隧道时，测点压力的第1次上升①是列车头部驶入隧道时产生的初始压缩波传播到测点引起的；测点压力的第1次下降②是列车尾部驶入隧道时，产生的初始膨胀波传播到测点引起的；测点压力波的第2次下降③是初始压缩波在传播过程中遇到中间风井时，一部分压缩波以膨胀波的形式向隧道入口返回过程中传播到车体表面测点引起的。隧道内的压缩波与膨胀波在隧道入口与中间风井间不断反射，反射回来的压力波传播到测点，导致测点压力不断变化。当列车经过中间风井④时，测点压力剧烈变化，头车经过中间风井时产生的压缩波导致测点压力迅速增大；当列车经过中间风井时，中间风井处气流紊乱，测点压力剧烈变化；尾车经过中间风井时产生膨胀波，导致测点压力迅速下降。之后，车体表面测点压力变化逐渐趋于稳定。

当列车在站间运行时，在加速运行过程⑤中，车体表面测点主要在负压区波动，且压力缓慢降低，这是由于列车在启动加速过程中引起的压缩波不明显，从而削弱了测点在正压区的波动。列车在时刻⑥开始匀速运行，测点压力基本不变。当列车经过中间风井⑦时，车体表面压力迅速增大，并剧烈变化；当列车通过中间风井后，测点压力迅速减小至0 Pa 附近，并保持稳定。从时刻⑧开始，列车在隧道内减速运行⑨，由于地铁隧道较长且隧道出口无反射波返回，车体表面测点压力经历较小的正压波动后逐渐趋于平缓。

在不同运行工况下，地铁列车在隧道中运行过程中，车体表面测点的压力变化峰峰值沿车长方向的变化规律如图10所示，其中，测点距鼻尖量纲一距离为车体表面各测点距离鼻尖的水平距离x与列车高度H的比值。

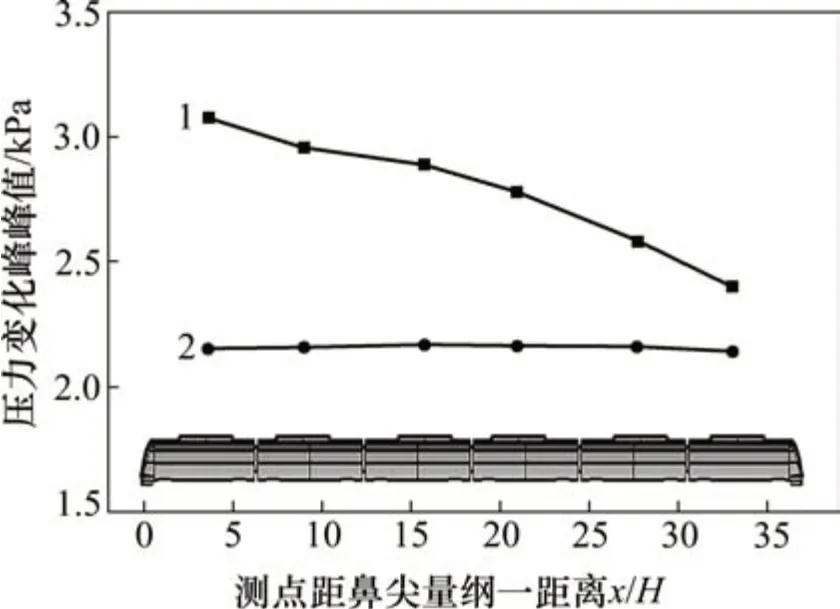
图10 不同运行工况下沿车长方向车体表面压力变化峰峰值Fig.10 Train surface’s pressure peak-to-peak value along length direction under different running conditions

从图10可以看出：列车由明线驶入隧道时，车体表面测点压力变化峰峰值沿车长方向从车头向车尾呈下降趋势；当列车在站间运行时，车体表面测点压力变化峰峰值沿车长方向变化较小，呈缓慢上升趋势；当列车由明线驶入隧道时，车体表面测点最大压力峰峰值是站间运行时的1.37倍。

由于地铁列车由明线驶入隧道时的车体表面压力变化峰峰值比列车站间运行时的压力峰峰值更大,即地铁列车由明线驶入隧道时的气动效应更加剧烈，因此，本文选择列车由明线驶入隧道这种运行工况对后续的隧道净空断面面积优化问题进行研究。

4 隧道合理净空面积

4.1 车内压力舒适性标准的选择

车内压力舒适性是评价列车乘坐舒适性的重要标准，而车内压力波动主要与地铁隧道阻塞比和列车密封指数有关，因此，有必要根据气压变化环境下人体舒适性准则，对密封指数不同的地铁列车在不同阻塞比的隧道中运行时的车内压力变化进行研究，从而确定列车密封指数与隧道净空断面面积的匹配关系。

当地铁列车车内的压力变化幅值及压力变化率超出某个临限值时，会影响司乘人员的乘坐舒适性[2]，甚至引起呕吐、失聪，因此，有必要对列车车内的压力变化进行限制。不同国家和地区所制订的气压变化环境下人体舒适性标准不相同[14]，其中，部分国家和地区的相关压力舒适性标准如表2所示[15]。

表2中，我国“地铁设计规范”适用于地铁列车最高运行速度不超过100 km/h 时的情况，而时速为140 km/h 高速地铁隧道的压力舒适性标准尚无依据可循，为此，本文综合借鉴我国“地铁设计规范”及高速铁路单线隧道的压力舒适性标准，分别计算列车密封指数与阻塞比的对应关系，再将2种压力舒适性标准下的密封指数与阻塞比的对应关系进行对比分析，得到地铁隧道净空断面面积及列车密封指数的合理建议值。

其中，我国“地铁设计规范”的压力舒适性评定标准为：当隧道内空气总压力变化值超过700 Pa 时，车内压力变化率dpi/dt不得大于415 Pa/s。我国高速铁路单线隧道的压力舒适性评定标准为：车厢内3 s 压力变化幅值(即任意3 s 内的压力变化峰峰值)小于800 Pa。

表2 各国隧道压力控制标准Table 2 Tunnel pressure control standards in various countries

4.2 合理净空断面面积的选择

假定车内压力变化率与车内外压差呈正比[11]，即

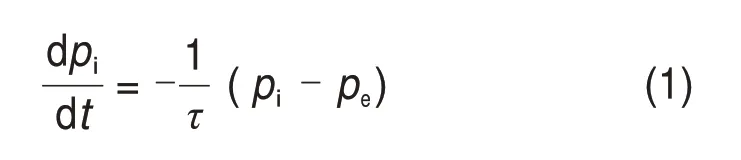
式中：pi为车内部压力；pe为车外部压力；τ为列车密封指数。式(1)可以等效成

由式(2)可得车内压力递推公式：

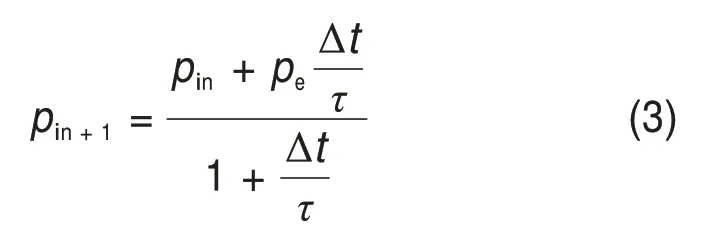
式中：Δt为数值计算过程中的时间步长。

在初始时刻t=0 s 时，pi0=0，车内压力变化可以通过式(3)由车外压力变化迭代计算得到。

图11所示为地铁列车匀速驶入截面积为26 m2隧道过程中，车体表面1号测点的压力变化曲线及不同密封指数下对应位置的车内压力变化。

由图11可见：受列车密封指数影响，车内压力变化小于车体表面压力变化；随着密封指数降低，车内压力逐渐接近车体表面压力。

图11 不同密封指数下车体表面1号测点的车内外压力变化Fig.11 Pressure variation of No.1 measurement point on train’s surface inside carriage with various tightness indexes

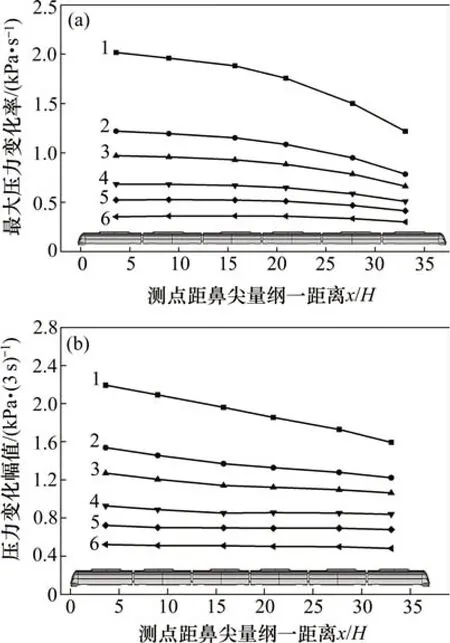
图12 不同密封指数下沿车长方向车内压力变化曲线Fig.12 Carriage pressure variation along length direction with different tightness indexes

在不同密封指数下，沿车长方向的车内最大压力变化率及3 s时压力变化幅值如图12所示。由图12可见：当列车由明线驶入隧道时，车内最大压力变化率及3 s 压力变化幅值从头车向尾车呈下降趋势；随着密封指数增大，车内最大压力变化率及3 s 压力变化幅值均减小，变化趋势趋于平缓；当列车由明线驶入隧道时，车内压力变化从车头向车尾呈下降趋势，因此，可以将头车1号测点对应位置的车内压力变化作为评定压力舒适性的标准。

高速地铁列车在匀速驶入不同阻塞比隧道的过程中，头车1号测点对应位置的车内最大压力变化率及3 s 压力变化幅值与阻塞比的关系曲线如图13所示。

图13 不同密封指数下车内压力变化与阻塞比关系曲线Fig.13 Relation curves of carriage pressure variation and blockage ratio with different tightness indexes

在图13中，车内最大压力变化率及3 s压力变化幅值与阻塞比的关系趋势线及决定系数R2如表3与表4所示。表3与表4中，车内最大压力变化率及3 s 压力变化幅值均与阻塞比服从幂函数关系，并且R2在0.99以上。

表3 不同密封指数下最大压力变化率与阻塞比关系趋势线Table 3 Corresponding relations between the maximum pressure variation rate and blockage ratio with different tightness indexes

表4 不同密封指数下3 s压力变化幅值与阻塞比关系趋势线Table 4 Corresponding relations between pressure variation amplitude in 3 s and blockage ratio with different tightness indexes

根据图13(a)和表3所示的车内最大压力变化率与阻塞比的关系曲线及趋势线可以得到不同列车密封指数下，当满足我国“地铁设计规范”中的压力舒适性评定标准(pt<415 Pa/s，Δp≥700 Pa)时，地铁列车运行所需的阻塞比β1与相应的隧道截面积At1，其中，列车密封指数与阻塞比的对应关系如表5所示。

同样，根据图13(b)与表4中的车内3 s 时压力变化幅值与阻塞比的关系曲线及趋势线可以得到不同列车密封指数下，当满足我国高速铁路单线隧道的相关压力舒适性控制标准([p]<800 Pa/(3 s))时，地铁列车运行所需的阻塞比β2与相应的隧道截面积At2，其中，列车密封指数与阻塞比的对应关系如表6所示。

将表5和表6中相同列车密封指数下对应的阻塞比进行对比发现：同一列车密封指数对应的At1比At2更大，即在相同列车密封指数下，“地铁设计规范”中对At的要求比高速铁路单线隧道中对At的要求更高，因此，可以选取表5中隧道截面积At1与列车密封指数的匹配值作为隧道净空断面面积优化的参考值，即根据“地铁设计规范”中的相关压力控制标准，匹配隧道净空断面面积与列车密封指数。

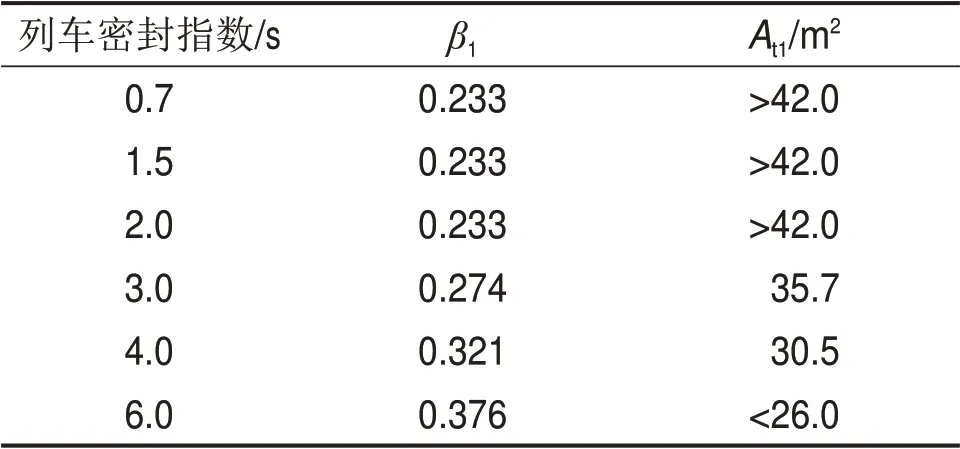
表5 满足“地铁设计规范”中压力舒适性标准时的列车密封指数与阻塞比的对应关系Table 5 Corresponding relations between tightness index and blockage ratio when meeting requirement of pressure comfort standard in“Code for design of metro”

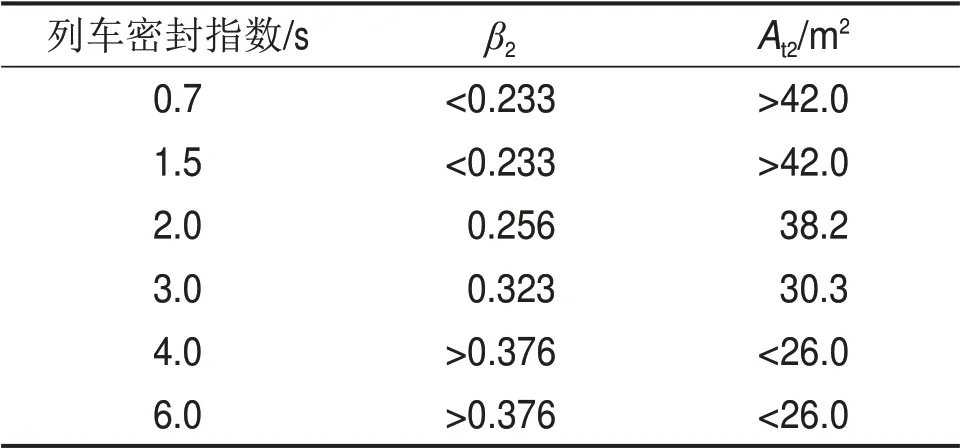
表6 满足高速铁路单线隧道中压力舒适性标准时的列车密封指数与阻塞比的对应关系Table 6 Corresponding relations between tightness index and blockage ratio when meeting requirement of pressure comfort standard in high-speed railway singlelane tunnel

由表5可知速度为140 km/h的高速地铁列车在不同阻塞比的隧道中运行，当满足我国“地铁设计规范”中的压力舒适性评定标准(pt<415 Pa/s，Δp≥700 Pa)时，需满足以下条件：

1) 当采用目前120 km/h 速度等级地铁常用的隧道断面面积26 m2时，地铁列车密封指数需达到6 s；

2)当地铁列车密封指数为4 s 时，地铁隧道净空断面面积需增大到30.5 m2；

3)当地铁列车密封指数为3 s时，地铁隧道净空断面面积需要增大到35.7 m2。

5 结论

1) 速度为140 km/h 的高速地铁列车在隧道中运行时，需满足以下条件：当采用目前120 km/h速度等级地铁常用的隧道断面面积26 m2时，地铁列车密封指数需达到6 s；当地铁列车密封指数为4 s和3 s时，地铁隧道净空断面面积需分别增大到30.5 m2和35.7 m2。

2)地铁列车由明线驶入隧道时的气动效应比列车站间运行时的气动效应更加严重。

3)当高速地铁列车由明线驶入隧道时，不同列车密封指数下的车内压力变化与阻塞比服从幂指数关系；阻塞比越大，车内压力变化越大。