超高填方荷载下刚柔组合桩复合地基的加固机理及其优化设计

豆红强，俞仰航，聂文峰，王浩，陈雷，张蕊

(1.福州大学环境与资源学院，福建福州，350116；2.地质工程福建省高校工程研究中心，福建福州，350116；3.中铁二院昆明勘察设计研究院有限责任公司，云南昆明，650200)

近年来，随着我国经济的飞速发展，进行了大规模的公路和铁路建设；在地势较为平坦的东部地区，铁路网及公路网的建设已经较为完善；而在我国的西部地区，由于自然、历史、社会等原因，交通基础设施建设较为落后。伴随着我国西部大开发战略实施，东西部区域经济的协调发展，势必要在西部地区进行大规模的公路和铁路建设。西部地区地势陡峭，地形地貌复杂，海拔高差大，且存在大部分的软土地基，在此地区修建铁路，不可避免地会遇到软弱地基上填筑高填方路堤的问题。为此，在高填方路堤荷载下，采用何种地基加固技术以确保铁路路基稳定并控制其变形，必要时能节约工程造价是当前亟需解决的问题。目前，桩式复合地基加固技术在高速铁路软基处理中得到了广泛的应用。如传统的碎石桩复合地基，因其取材方便，造价较低就常常用于软基处理。碎石桩可以通过增大桩径来提高复合地基的承载力，故路堤沉降量一般能满足要求[1]，但由于其侧向约束作用较弱，路堤的侧向变形难以保证，国内外发生不少碎石桩复合地基的失稳滑塌事故；如台华高速公路某路堤[2]，采用干振碎石桩对软基进行处理，当路堤填筑到4.5 m时，路堤边坡处下覆软土层中产生大范围的塑性区，路堤发生整体失稳滑移。而以PHC 管桩等为代表的刚性桩复合地基技术，相较于传统的柔性桩复合地基，PHC管桩复合地基因其施工速度快，可大幅度提高复合地基承载力并显著减小地基变形等优点，在现阶段的复合地基处理中广泛被使用[3]；国内外众学者亦通过现场试验[4-6]、模型试验[7-8]、数值模拟[9-11]及理论分析[12-14]等手段对其工作机理开展了详细研究。尤其是郑刚等[15]借助数值分析软件，指出路堤荷载下刚性桩复合地基不同位置的桩体破坏模式有较大差异，并将路堤下土体和桩体分为拉弯区、弯剪区、压弯区和承压区4个区。然而，针对现有的桩式复合地基加固技术及其加固理论，仍存在一些问题：1)所研究的路堤填土高度均较低，超高填方路堤(填土高度大于20 m)则较少涉及；2)多数局限于单一桩型路堤失稳破坏模式的研究，未考虑采用组合桩对地基进行联合处理，对其加固机理则未涉及。针对上述所存在问题，依托玉溪—磨憨铁路普洱车站超高填方工程，根据超高填方路堤荷载下不同位置桩体的受荷特点以及刚、柔性桩二者控制侧向变形能力差异，本文作者提出一种刚柔组合桩复合地基的优化设计方法，对解决传统碎石桩复合地基侧向变形过大、稳定性不足以及工程造价过高等问题提供一种有益的尝试。同时，借助ABAQUS数值分析软件，分析刚柔组合桩复合地基的加固机理与其相较于传统桩式复合地基的优越性。

1 工程概况

玉溪—磨憨铁路全线位于地形地貌复杂、地层岩性起伏变化较大的云南省南部地区。线路全长约为513.8 km，其中以48.03 km的铁路干线坐落在软土地基之上。软土厚度变化显著，且多以淤泥质土、泥炭质土、松软土等为主。以普洱车站为例，车站位于构造剥蚀形成的思茅向斜盆地西侧，属低中山地貌，地面高程为1 327～1 570 m，最大高差为200 m，自然横坡为5°～25°，局部较陡。山间浅沟发育，地形波状起伏，沟槽等低洼地带覆土较厚；其中DK269+730～DK269+930 段路基以填方形式通过，填方高度为21.6 m，基底分布达11.3 m淤泥质土层。

原设计中拟采用2 种不同方案对软基进行处理，方案1：采用PHC 管桩复合地基对软基进行处理，其中PHC 管桩外径为500 mm，壁厚为100 mm，设计桩长13.8 m，桩间距为2.0 m，按正方形布桩，桩顶处设长×宽×高为1.60 m×1.60 m×0.45 m的钢筋混凝土盖板。同时，地基表面铺设0.60 m厚土工格栅碎石垫层，垫层中央铺设屈服强度为80 kN/m的两层双向土工格栅。填土选用TB 10001—2016“铁路路基设计规范”规定的A 和B 组填料，压实度控制在90%以上。方案2：采用强夯碎石墩对软基进行处理，其中强夯碎石墩桩径为1.5 m，设计桩长为12 m，桩间距为3 m，三角形布桩；其余设计与方案1相一致。典型的工程地质剖面图如图1所示。

2 数值模型及计算参数

根据上述2个方案，分别借助ABAQUS软件，建立2个数值分析模型，为了简化计算模型，仅取图1中的右侧区域进行计算分析。

2.1 PHC管桩复合地基数值模型(方案1)

1)几何模型及边界条件。根据PHC 管桩桩长13.8 m，正方形的布桩条件，以及考虑到填土中最长的土工格栅长度38 m，选取试验段中一典型的三维条形区域，取模型深度为60 m，模型长度为200 m，模型厚度为2 m，以消除边界条件的影响；并结合工程实际情况，取路堤填土高度为21.6 m。模型中PHC管桩采用半桩，桩间距设置为2 m。模型底部X，Y和Z3 个方向的位移均被约束，模型左右两侧X方向的位移被约束，模型前后两侧Y方向的位移被约束。具体模型如图2所示，土工格栅采用不受压的M3D4 膜单元，其余均采用C3D8R实体单元，通过软件中“生死单元控制”实现路堤碎石垫层及填土的逐级加载。通过Embedded Region 内置接触方式来模拟土工格栅与褥垫层中的碎石填料存在的嵌锁作用。

2)计算模型及参数。地基土、填料以及碎石垫层采用摩尔-库仑弹塑性模型，土工格栅则采用线弹性模型；其计算参数可由勘察报告和当地经验确定，如表1所示。PHC管桩采用混凝土损伤塑性模型(CDP)，该模型能较好地模拟桩体破坏过程中随着桩身裂缝的扩展，桩体损伤度逐渐增加，所受截面应力下降，桩身内力重分布的过程；同时相比常规的线弹性模型，解决了桩体受弯破坏后，桩身弯矩和剪力仍能继续增大，桩身位移计算偏小等问题，可较合理地模拟PHC 管桩的力学性能[16]。该模型引进拉伸损伤dt和压缩损伤dc这2个变量来反映桩体的损伤程度，该变量可表示为初始弹性模量和等效塑性应变的关系[17]：

图1 典型地质剖面图Fig.1 Typical geological profile

图2 有限元模型网格划分Fig.2 Finite element model mesh

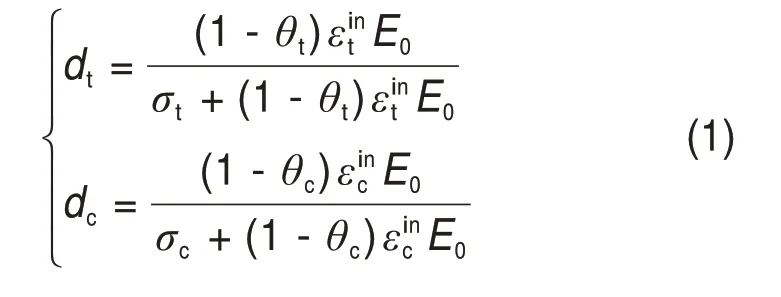
式中：E0为混凝土初始弹性模量；εint和εinc分别为混凝土受拉和受压塑性应变；σt和σc分别为混凝土受拉应力和受压应力；θt为受拉塑性应变与非弹性应变的比值；θc为受压塑性应变与非弹性应变的比值。利用GB 50010—2010“混凝土结构设计规范”所提供的混凝土材料的应力-应变关系曲线[18]，结合式(1)即可确定混凝土损伤模型所需的计算参数，如图3所示。

2.2 强夯碎石墩复合地基数值模型(方案2)

对比PHC 管桩复合地基数值模型，强夯碎石墩复合地基数值模型主要区别有以下几点：1)在几何模型尺寸上，由于强夯碎石墩复合地基采用三角形布桩，桩间距设置为3 m，故模型的厚度取为2.6 m，具体的模型图如图2(c)所示；2)在桩的模型上，强夯碎石墩采用摩尔-库仑弹塑性模型，其具体参数如表1所示。其余边界条件、几何尺寸、计算模型以及材料参数等均与PHC 管桩复合地基数值模型设置一致。

3 计算结果

3.1 2种原设计方案下塑性区开展及稳定性分析

等效塑性应变云图能较好地描述土体塑性区域的发展及贯通趋势，同时能获取路堤潜在的滑裂面。图4所示为2个模型强度折减步下输出的等效塑性应变云图。由图4可知：以PHC 管桩支承的路堤，其潜在的滑裂面从路堤顶面的填土一直贯通到路堤下覆的软土层中，并从坡脚外侧剪出；对比强夯碎石墩支承的路堤，其潜在滑裂面的规模与所在位置与PHC 管桩复合地基基本一致，亦始于路堤顶面处的填土层，与路堤边坡处的下覆软土层连接贯通，最后从坡脚的外侧出露。二者的滑裂面均穿过填土中长条土工格栅外缘，其中剪入口均位于路堤坡肩正下位置的软土层，剪出口位于路堤坡脚位置。同时，基于强度折减法，分别求得了二者的安全系数，其中以PHC 管桩支承的路堤安全系数高达4.0，远大于强夯碎石墩复合地基的安全系数1.375。表明采用PHC管桩对软土地基予以处理，其安全性能得到保证，并且存在可优化的空间，而若采用强夯碎石墩予以处理，安全系数偏低。

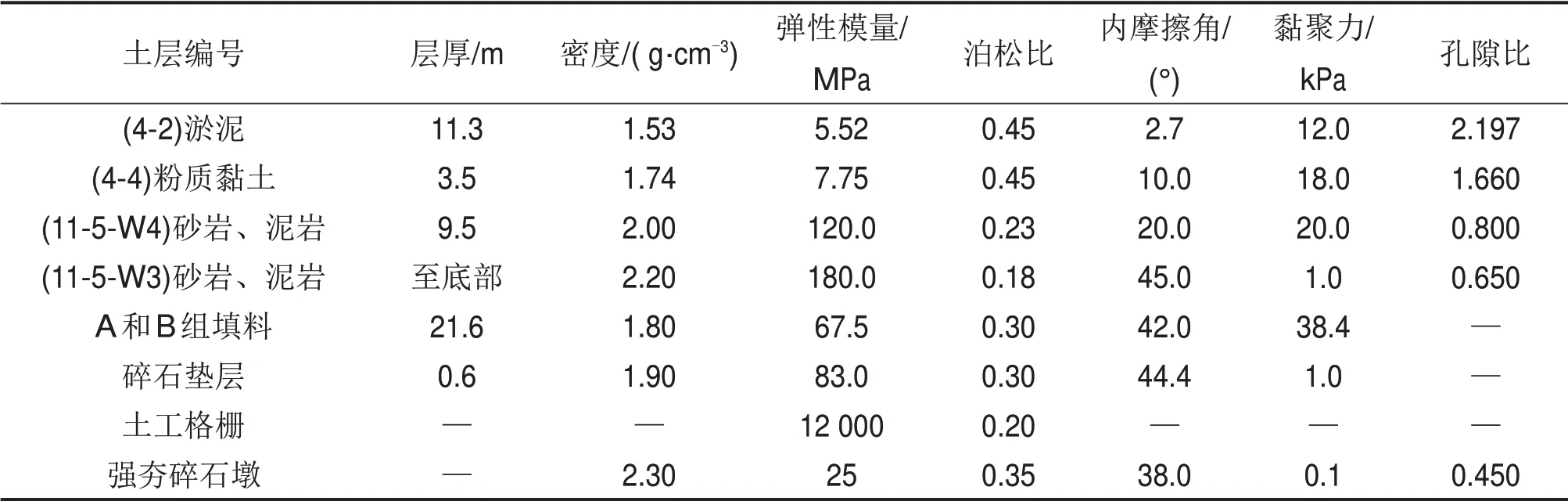
表1 模型的计算参数Table 1 Calculating parameter of numerical model

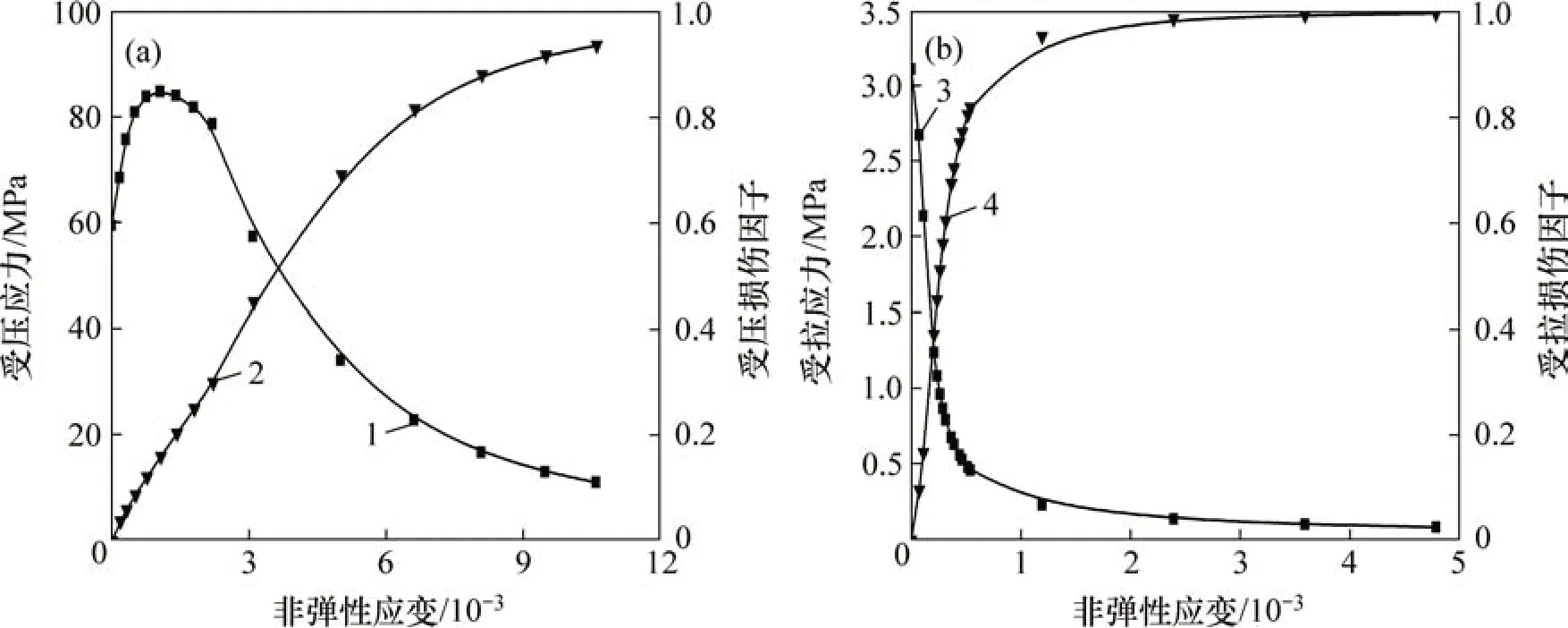
图3 混凝土损伤塑性模型参数Fig.3 Calculating parameters of CDP model

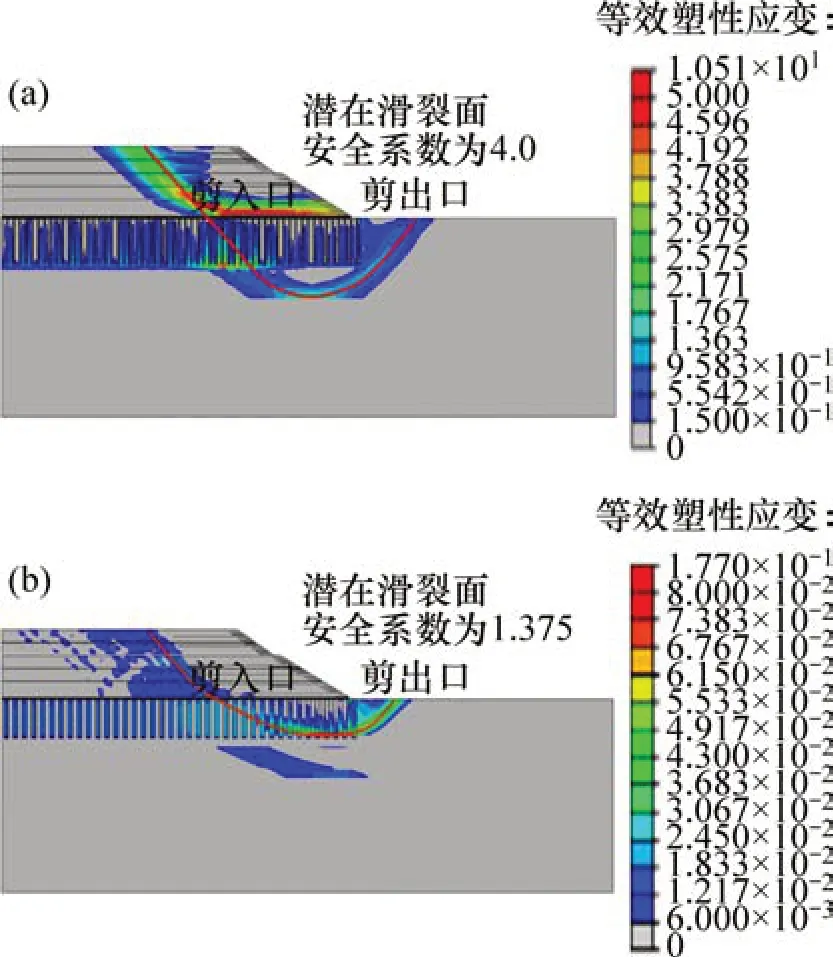
图4 2种方案塑性区分布情况Fig.4 Distribution of plastic zones of two options

3.2 方案1中PHC管桩桩身受力讨论

为分析在超高填方路堤荷载下不同位置桩的受荷特点，取图2(b)中所示4根PHC管桩对其桩身弯矩及剪力进行分析，对比图4(a)路堤的塑性区分布情况，可知A位于潜在滑裂面剪出口，B位于潜在滑裂面剪入口，C和D位于路堤中部。由于强夯碎石墩在模型中桩身剪力和弯矩均较低，故不进行对比分析。图5(a)所示为路堤堆载完成后PHC管桩的桩身弯矩图。由图5(a)可知：A和B桩身弯矩较大，两桩的弯矩曲线分布相似，桩身出现2个拐点，分别位于桩顶位置以及桩身8 m处。B弯矩极值为-78 kN·m，出现在桩顶附近，其绝对值大于A 桩身弯矩最大值54 kN·m。而位于路堤中部的C和D桩身弯矩较小，其中C桩身弯矩均小于5 kN·m，D桩身弯矩最大值出现在软硬土层交界处，其值不超过30 kN·m。图5(b)所示为路堤堆载完成后PHC管桩的桩身剪力图。从图5(b)可知：A和B桩身剪力较大，最大值出现在桩顶位置，分别为54 kN和45 kN，而位于路堤内部的PHC管桩，桩身剪力总体上较小，其中C剪力几乎接近于0 kN，D桩身剪力最大值也仅为32 kN。基于上述分析，表明路堤的边桩，由于其位于潜在的滑裂面处，阻止滑裂面形成和发展，承担高填方路堤的侧向荷载及剪切荷载，桩身所受弯矩及剪力均较大，而位于路堤中心的PHC 管桩，主要支承高填方路堤的竖向荷载，桩身所受剪力和弯矩较低，PHC 管桩的抗弯性能以及抗剪性能未得到充分的利用。

图5 典型位置PHC管桩桩体受力Fig.5 Distribution of typical position PHC pipe stresses

4 优化方案

路堤的失稳破坏往往伴随着滑裂面的形成与发展，倘若复合地基处理技术能较好地阻止滑裂面的发展，则必将极大地提高路堤的稳定性及其安全性。为此，基于上述研究，本文提出一种超高填方荷载下刚柔组合桩复合地基优化设计方法，该方法依据超高填方路堤荷载下不同位置桩体的受荷特点以及刚、柔性桩二者控制侧向变形能力差异，将较高抗弯及抗剪强度的刚性桩布设在超高填方路堤潜在的滑裂面剪入口或剪出口位置，其余位置布置造价较低的柔性桩；通过发挥少部分PHC 管桩的抗弯、抗剪性能，阻止潜在滑裂面的进一步形成与发展，增加了路堤的稳定性及安全性，同时又兼顾工程造价经济合理。为分析其加固机理和加固效果，本文基于上述方法建立2个优化设计方案。方案3：桩体布置以强夯碎石墩为主，将PHC 管桩布设在潜在滑裂面剪入口处，共布设4排PHC管桩，桩间距设置一致为3 m，桩长为13.8 m，采用正三角形布桩；方案4：桩体布置以强夯碎石墩为主，将PHC 管桩布设在潜在滑裂面剪出口处。共布设6 排PHC 管桩，桩间距设置一致为3 m，桩长为13.8 m，采用正三角形布桩。方案3和方案4除桩型布设与前述模型不同外，其余(包括计算参数、本构模型的选取等)均与先前方案1和方案2所建数值模型相同。其具体优化方案模型如图6所示。

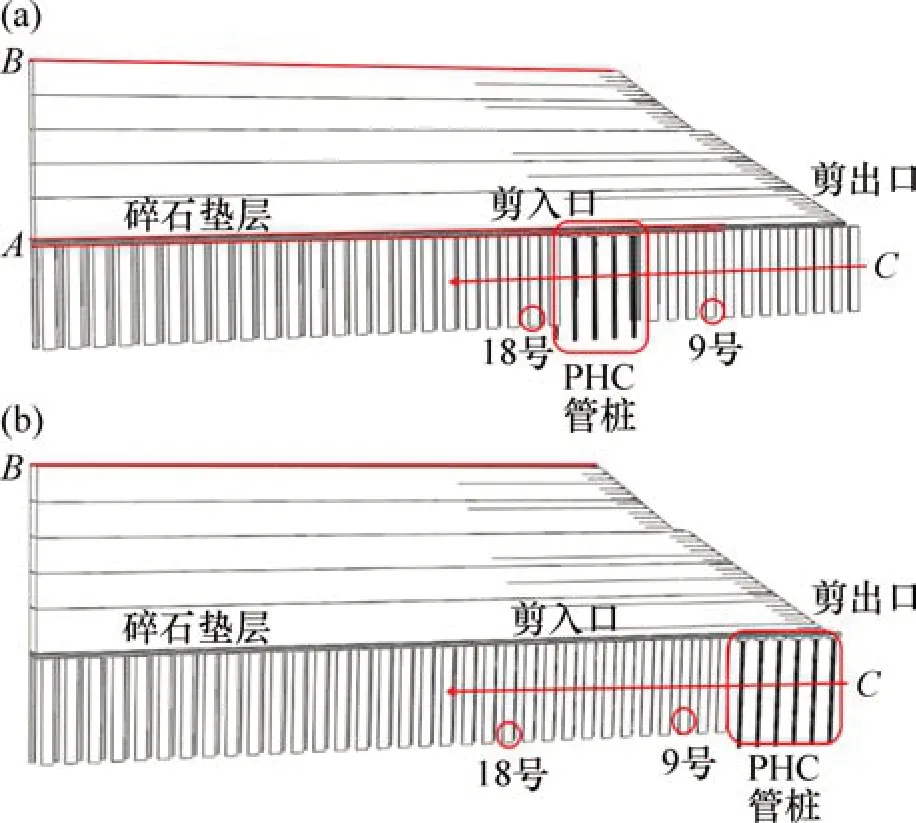
图6 优化方案数值模型Fig.6 Numerical model of optimization scheme

本文所建优化设计方案需事先考虑潜在滑裂面所处位置，因此，对于一般工程而言，可以通过数值分析、测斜管监测等手段获取较为准确的滑裂面位置。而对于一些无法采取该手段的工程，本文作者在多种工况的数值分析研究基础上，得出路堤中的长条土工格栅埋设对滑裂面形成有较强的阻断作用，且滑裂面剪入口基本位于坡肩正下土层范围内，因此，可根据路堤中的长条土工格栅外缘位置及路堤坡肩粗略判别滑裂面分布。

5 优化方案对比分析

5.1 侧向变形分析

图7所示为路堤堆载完成后全强夯碎石墩复合地基、2 种组合桩复合地基3 种方案下典型桩侧向位移曲线图。典型桩具体所在位置如图6所示，9号位于剪入口外侧，18 号剪入口内侧。由图7可知：剪入口外侧桩侧向位移总体上大于剪入口内侧桩侧向位移，桩身弯曲程度更为明显。表明剪入口处以及剪入口外侧为路堤阻滑的关键位置，桩身承受更大的侧向荷载，较剪入口内侧桩产生更大变形。由图7(a)可知：在2种组合桩复合地基方案下，对比全强夯碎石墩复合地基，位于剪入口外侧的9号桩身侧向位移均大幅度减小，其中以PHC 管桩布设在剪入口条件下，桩身侧向位移下降最为明显；桩身曲线较全强夯碎石墩复合地基的“弓形”过渡为线性分布。究其原因有2点：1)PHC 管桩布设在剪入口位置，最先于其他桩体发挥抗弯、抗剪作用，桩体承担了大部分的水平应力和剪切应力，阻止了土体塑性区的进一步发展；2)PHC 管桩桩身刚度大，嵌入土层较深，抵抗变形能力强，一定程度限制了剪入口外侧桩周土的移动。而将PHC 管桩布设在剪出口位置，由于在此之前剪入口处土体塑性区域已充分发展，土体中较大的剪切应力及水平应力向剪入口外侧桩传递，桩身已产生较大的侧向变形，虽然剪出口处PHC 管桩发挥较大的拦挡作用，但效果甚微。由图7(b)可知：位于剪入口内侧18 号桩身侧移曲线却呈现出不同的特点，PHC 管桩布设在剪出口条件下，18 号的桩身侧向位移较全强夯碎石墩复合地基条件下略有降低，而布设在剪入口处，18 号桩身侧向位移不降反升，且桩身曲率增大。究其原因在于将PHC 管桩布置在滑裂面剪入口位置，一方面阻止了该剪入口处土体塑性区域向路堤外侧发展，另一方面也使该处的土体的塑性区域向剪入口内侧发生分散，导致该处部分土体进入塑性屈服状态，位于剪入口内侧桩体应力增大，侧向位移增加。

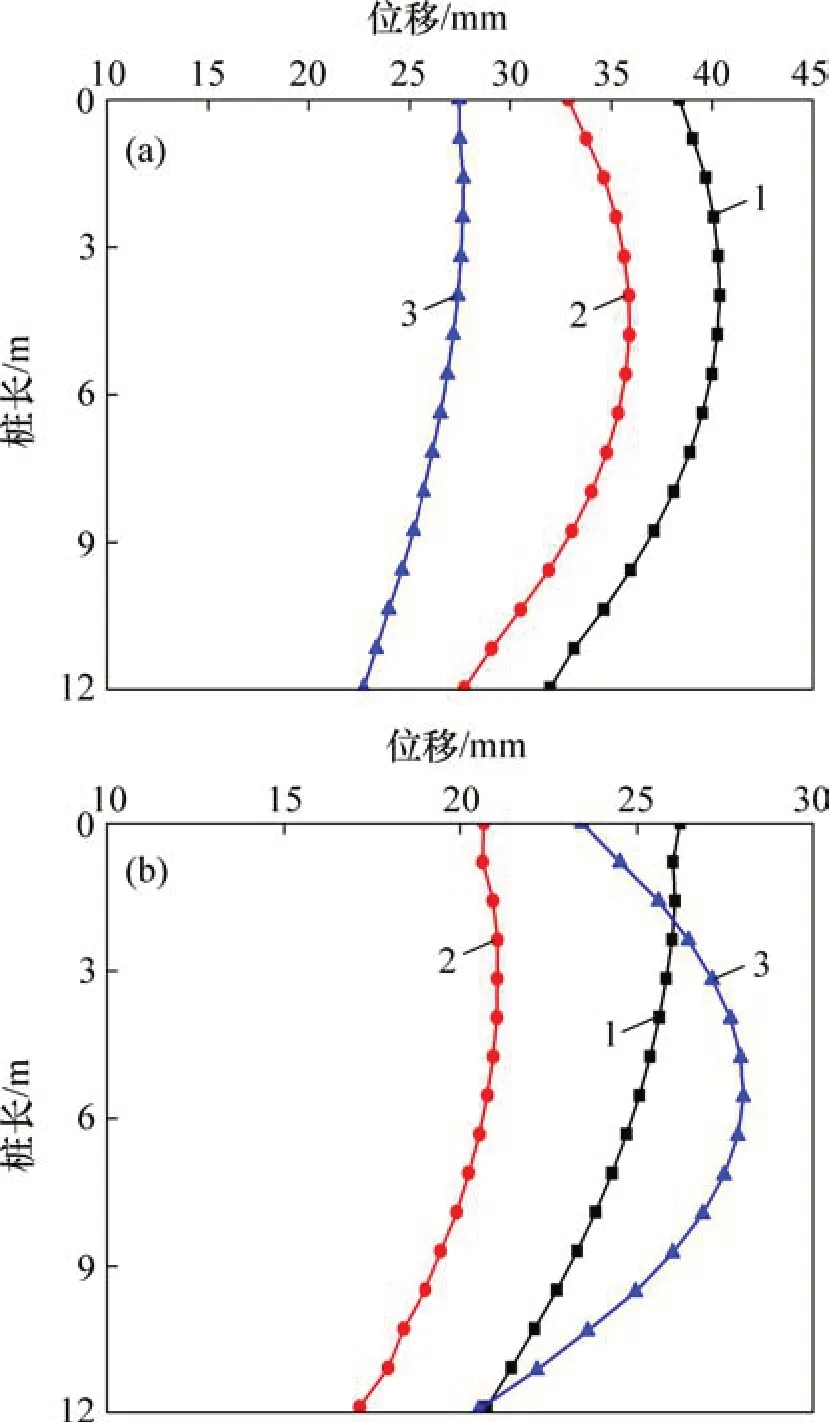
图7 典型桩侧向位移曲线Fig.7 Lateral deflections of typical position pile

为进一步说明组合桩复合地基良好的控制变形效果，特取图6中的C点所示路径作出桩间土水平位移曲线进行分析，该路径为地基土体水平位移最大值所在路径。图8所示为路堤堆载完成后3种方案下地基土体水平位移变化曲线图。由图8可知：3 种方案下，方案2 全强夯碎石墩复合地基的土体水平位移最大，曲线呈现出“勺形”分布的特点，水平位移极大值区域位于距C点15 m 的土层区域；方案4，在剪出口位置布设PHC 管桩后，桩间土的水平位移均得到不同程度减小，局部土体水平位移减少超过6 cm，值得说明的是，曲线依旧呈现出“勺形”，但其水平位移极值点略微向路堤内部移动，表明PHC 管桩在剪出口直接布设处(布设区域0～15 m)，土体水平位移显著降低，极值点内移。而方案3，在剪入口处布设PHC 管桩后，水平位移曲线则表现出不同的特点；与方案2相比，剪入口以及剪入口外侧的土体水平位移显著降低，尤其表现在剪入口位置，尽管此处仅采用4 根PHC 管桩，但大部分土体位移减少均超过10 cm，降幅超过30%；相比而言，在剪入口布设PHC 管桩其控制侧向变形效果更加明显。另一方面，方案3曲线在剪入口内侧，存在上升段，且在距C点距离50 m 处，土体位移大于全碎石墩复合地基位移，这是因为剪入口处布设PHC 管桩后，使该处土体的塑性区域向剪入口内侧发生分散，导致该处部分土体进入塑性屈服状态，土体的位移略微增加，这与前述分析相一致。

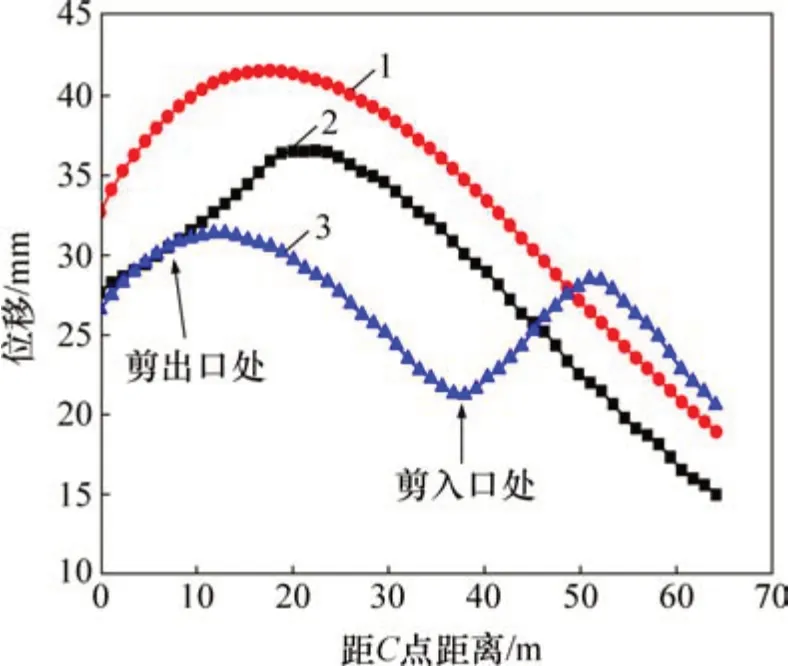
图8 典型断面地基土水平位移曲线Fig.8 Lateral displacement curves at typical sections of foundation soil

5.2 竖向变形分析

取图6(a)中A点所示路径作土工格栅垫层顶底面的沉降曲线如图9(a)所示。由方案2 和方案3 的垫层顶面曲线对比可知：方案3 在剪入口处布置PHC 管桩后，使该处地基的沉降量显著降低；同时，在距离路堤中线70 m 左右位置，即位于路堤剪入口位置，方案3垫层底面沉降曲线呈现出尖刺状，且曲线出现明显的爬坡段和陡降段，这是由于此处布置的PHC 管桩，桩间距较大，且嵌固于硬土层中，在高填方路堤荷载下，桩和下卧硬土层均较难压缩，桩土间差异沉降显著，桩体出现上刺所致。同时，由于柔性桩和刚性桩显著的刚度差异以及控制竖向变形能力的不同，二者共同支承路堤时，在柔性桩与刚性桩过渡段亦会产生较明显的差异沉降，对应于曲线的爬升段和陡降段。而在其上方铺设0.6 m的双层土工格栅垫层之后，从方案3垫层顶面沉降曲线图可知，桩和桩间土的差异沉降显著降低，原曲线的尖刺状变得平滑，同时柔性桩与刚性桩过渡区域，因桩型不同而引起的差异沉降也得到明显的改善。表明双层土工格栅碎石垫层在协调桩和桩间土的不均匀沉降以及不同刚度桩体过渡段的差异沉降发挥了重大作用。

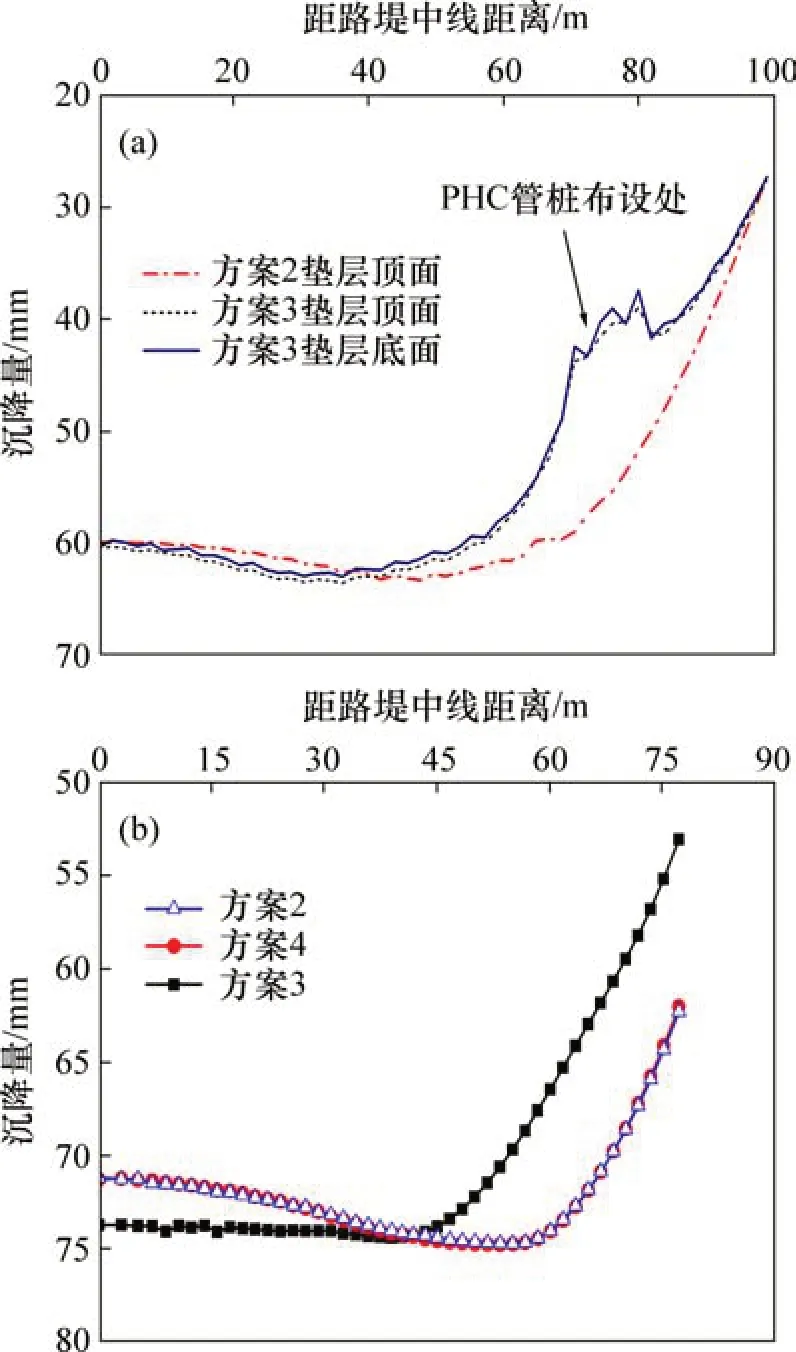
图9 典型断面路堤竖向变形曲线Fig.9 Vertical deformation curves at typical sections

取图6中B点所示路径作出路堤顶面的沉降曲线如图9(b)所示。由图9(b)可知：3 种方案下，路堤沉降规律表现出路面中心处沉降较大，靠近路肩处沉降较小的特点。方案2与方案4相比，路堤顶面的沉降曲线基本无区别，其原因在于剪出口布设的PHC 管桩，主要的作用是抗弯、抗剪、控制路堤的侧向变形，仅支承少部分带坡率的路堤边坡竖向荷载，对路堤的竖向变形影响较小，故将强夯碎石墩替换成PHC 管桩并未引起路面沉降的改变；方案2 和4 与方案3 相比，沉降曲线存在明显的下降段，这是由于距离路堤中线40 m 处，该处正好对应于填土中潜在滑裂面起始位置(图4(b)所示)，土体产生较大的滑移所致，而方案3 的曲线则较为平缓，表明在剪入口布设PHC管桩后，其一定程度上阻止了填土中滑裂面的发展。由方案3 沉降曲线分析可知，在剪入口布设PHC 管桩，其对路堤顶面沉降影响主要表现在2个方面，一是靠近坡肩处路堤顶面的沉降大幅减小，二是离路面中心40 m 的范围内，路堤顶面的沉降量略有增加。这是因为剪入口范围内布设的PHC 管桩的刚度大，桩体分担较大的荷载，桩间土所承当的荷载比例减小，桩间土沉降随之减小。同时PHC 管桩将路堤的荷载传递到深部较硬的土层，桩体本身和下部坚硬土层均较难压缩，从而使坡肩处路堤顶面的沉降大大降低。而路堤中心处沉降略有增加则是因为强夯碎石墩和PHC 管桩二者控制竖向变形能力不同，剪入口布设的PHC 管桩使该处地基表面较原强夯碎石墩复合地基沉降大大降低，虽有土工格栅碎石垫层协调竖向变形，但仍然出现PHC 管桩加固处土体集体向上“隆起”的现象如图9(a)所示，改变了路堤填土的原有应力场，使路堤中心处沉降略有增大。

5.3 塑性区开展与稳定性分析

图10 2种优化方案塑性区分布情况Fig.10 Distribution of plastic zones of two optimization schemes

借助于有限元强度折减法，图10所示为2 种组合式复合地基的潜在滑裂面与其对应的安全系数。从图10(b)可知：当PHC管桩布设于潜在滑裂面的剪出口时，其可以显著分担PHC 管桩桩周土体所受的剪切应力，使其塑性区向四周分散，而不似图4(b)中的强夯碎石墩在该处出现塑性区集中。同时，该处PHC 管桩的存在可阻断塑性区的贯通，使其向深处发展。其对应的安全系数则达到2.16，完全满足工程设计的要求。相应地，当PHC 管桩在滑裂面剪入口时(见图10(a))，联合土工格栅，该处PHC 管桩的存在直接阻止剪入口处地基土体塑性区的发展，使其塑性区域向剪入口内侧发生分散，阻断了潜在滑裂面的形成，尽管此处仅采用4根PHC管桩，但由于其较大的抗弯、抗剪能力，该工况的安全系数仍高达2.27。

与此同时，亦可采用路堤坡脚处的最大侧向变形与路堤中心处最大沉降量的比值来衡量路堤的稳定性[19-20]：

式中：δhmax为路堤坡脚处的最大侧向变形；δvmax为路堤中心处最大沉降量。该比值越小，说明路堤的稳定性越高，若该值超过0.5，则路堤稳定性较低。

图11所示为4 种方案下路堤坡脚处最大侧向变形与路堤中心处最大沉降比值的直方分布图。由图11可知：全PHC管桩支承下的路堤(方案1)比值最低，全强夯碎石墩地基支承下的路堤(方案2)比值较高为0.49，该值接近于0.5，表明该方案下路堤稳定性偏低。而方案3和方案4采用PHC管桩进行联合处理后，该比值显著降低，其中尽管方案3在剪入口仅布设4排的PHC管桩，但其比值下降至0.32，稳定性提升最为明显，这与强度折减法求得的安全系数较为吻合。

图11 不同方案下路堤最大侧向变形与最大沉降量比值Fig.11 Ratio of maximum lateral deformation and maximum settlement of embankment under different schemes

5.4 加固效果以及经济性讨论

2种组合桩复合地基均能有效地控制路堤的侧向变形，方案3能显著降低剪入口以及剪入口外侧地基土体的侧向变形值，降幅超过30%，方案4使剪入口内侧和外侧的土体的水平位移均得到不同程度减小，但减小幅度较低；2种组合桩地基在控制路堤的竖向变形方面，效果并不显著，方案4对路堤顶面的沉降基本无影响，方案3能显著减少靠近坡肩处路面的沉降，但同时也使路堤中心处的沉降略有增加；安全性上，方案3的安全系数略高于方案4的安全系数；经济合理性方面，由于方案3仅采用4排PHC管桩，造价更低，经济效益更为显著；综上所述，方案3要优于方案4。

6 结论

1)普洱车站的超高填方路堤工程若采用PHC管桩复合地基，则路堤的边桩所受弯矩和剪力较大，而路堤内部桩所受剪力和弯矩较低，其抗弯、抗剪性能未得到充分的利用，路堤安全性较高，存在可优化的空间；而若采用全强夯碎石墩复合地基则表现为路堤边桩的侧向变形较大，桩体柔性弯曲明显，路堤安全性相对较低。

2)提出一种超高填方荷载下刚柔组合桩复合地基优化设计方法，其将较高抗弯及抗剪强度的刚性桩布设在超高填方路堤潜在的滑裂面剪入口或剪出口位置，其余位置布置造价较低的柔性桩；通过发挥少部分PHC 管桩的抗弯、抗剪性能，阻止潜在滑裂面的进一步形成与发展，增加了路堤的稳定性及安全性，同时又兼顾工程造价经济合理。

3)2种组合桩复合地基均能有效地控制路堤的侧向变形，方案3(PHC 管桩布置在潜在滑裂面剪入口)能显著减少剪入口以及剪入口外侧的土体水平位移，降幅超过30%，方案4(PHC 管桩布置在潜在滑裂面剪出口)使剪入口内侧和外侧的土体水平位移均得到不同程度减小，但减小幅度较低。二者在控制超高填方路堤顶面的竖向变形方面，效果并不明显，同时路堤中的双层土工格栅碎石垫层能较好地协调桩土间不均匀沉降，以及不同刚度桩体过渡段引起的差异沉降。

4)2种组合桩复合地基在阻止路堤土体塑性区发展、潜在滑裂面的形成和发展均发挥了较大的作用。方案3 在剪入口处的PHC 管桩存在直接阻断了潜在滑裂面的形成，使其塑性区域向剪入口内侧发生分散，安全系数为2.27；而方案4可显著分担PHC 管桩桩周土体所受的剪切应力，使剪出口的塑性区向四周分散，安全系数为2.16。