考虑结构表层粗糙度的混凝土桩-黏土界面剪切特性试验研究

汪优，李奕金，谭伟，汤明明，杜炜

(中南大学土木工程学院，湖南长沙，410075)

桩-土相互作用是岩土工程领域的研究热点问题[1-3]。现场试验证明：桩基受到竖向荷载时，桩-土相互作用是由桩-土接触面来传递的[4-6]。由于桩体与土体材料力学性质的差异、接触面粗糙度、外力、土颗粒和含水率等内外部因素的影响，使桩-土接触面产生错动、滑移或者开裂等非连续变形，力学特性变得异常复杂。因此，探究不同因素对桩-土接触面力学性质的影响规律，是研究桩基承载力、 沉降和变形等问题的基础。POTYONDY[7]在大量剪切试验基础上，指出接触面粗糙度、法向应力、土质和含水率是接触面剪切强度的主要影响因素。CHEN 等[8]开展不同粗糙度的混凝土板-红黏土接触面直剪试验，指出混凝土板表面凹槽数量对接触面粗糙度有显著影响，接触面内摩擦角始终小于土体自身内摩擦角。石熊等[9]通过开展红黏土-混凝土直剪试验，指出随着接触面粗糙度的增大，接触面抗剪强度及残余强度、黏聚力增大，内摩擦角减小。成浩等[10]在此基础上研究了粗糙度对接触面残余强度的影响，并提出接触面粗糙度的增加能够明显提高接触面残余剪切强度，但此种影响伴随着法向应力的增大而逐渐弱化。金子豪等[11]开展混凝土-砂土直剪试验，指出接触面峰值、残余应力比随法向应力的增大而减小，接触面峰值应力比随粗糙度对数lgR近似线性增长，同时指出砂土自身剪切强度不是混凝土-砂土接触面剪切强度的上限。张嘎等[12]开展粗粒土与人工粗糙钢板接触面剪切试验，指出接触面变形可分解为同时发生、相互影响的土与结构接触面上的滑移变形及结构面附近的土在约束之下的剪切变形2部分。陆勇等[13]采用高压直剪仪进行了砂砾与不同粗糙度钢板结构面接触剪切试验，提出接触面粗糙度对接触面力学特性有直接影响，中压与高压下接触面的力学特性呈现出不同的规律。刘方成等[14]利用改进的循环单剪试验系统开展不同法向应力、接触面粗糙度条件下粉质黏土-混凝土接触面剪切试验，指出接触面破坏主要分为接触面附近土体自身剪切破坏和接触面滑移破坏2种形式，且接触面粗糙度和法向压力越大，越趋向于土体自身剪切破坏。王佳等[15]进行了砂土与不同粗糙度表面的混凝土板的大型直剪试验研究，并指出界面粗糙度能够明显提高接触面抗剪强度，但随着法向应力的增大，粗糙度对接触面抗剪强度的影响逐渐减弱。黄东梅等[16]和卢照亮等[17]在风洞试验研究中分别采用砂纸模拟高层建筑物、斜拉索等建筑物表面由于材料尺寸的差异性导致的凹凸不平整。罗耀武等[18]在模型桩表面粘贴砂纸，以砂纸表面最大粒径衡量模型桩桩侧表面粗糙度，研究粗糙度对抗拔桩承载特性的影响。上述学者在大量试验的基础上，探究不同影响因素下接触面力学特性的变化规律，并取得了重大进展，对桩-土界面力学特性的研究具有借鉴意义，但还存在一些不足之处。例如，采用结构面上开挖规则形状孔槽的方法模拟混凝土-土接触面不同粗糙度，虽然简单易行，但侧重于从宏观角度分析粗糙度对接触面力学特性的影响，忽略了混凝土表面粗糙度的不规则性及孔槽与土颗粒尺寸相差较大时对接触面力学特性的影响，对于混凝土预制桩、挡土墙等采用模板浇筑结构，由于由施工控制条件、气候等其他因素而在其表面形成的不规则凹凸形状无法有效模拟；虽然有些学者人为制造不规则的混凝土表面粗糙度或者采用不同规格砂纸来从微观角度模拟结构物表面粗糙度，只是笼统的定义粗糙度，并未对结构物表层粗糙度进行深入研究，缺乏可定量的结构物表层粗糙度计算确定公式。因此，本文作者根据不同规格砂纸表面粗糙度指标的实测数据，建立起结构表层粗糙度的计算公式；然后，根据砂纸规格与结构表层粗糙度之间的定量关系，采用不同规格砂纸模拟混凝土桩-黏土界面处结构物与土体接触表层的粗糙度变化，开展混凝土桩-黏土接触界面剪切试验研究，定量分析结构表层粗糙度对桩-土界面剪切特性的影响及其规律，为桩-土界面力学特性和试验研究提供参考。

1 结构表层粗糙度的确定

灌砂法、针触法和粗糙度测定仪法是土木工程中3 种常用的测定混凝土结构表层粗糙度的方法[19]，其本质是采用物体表面基准面以上凸部分的体积或者面积与其基准面面积或长度的比值求得物体的表面粗糙度。因此，本文采用文献[20]中SJ-410 型号的粗糙度测量仪，对不同规格的砂纸进行测量，获得了相应的结构物表层粗糙度指标Pa(原始轮廓算术平均值)，如表1所示。

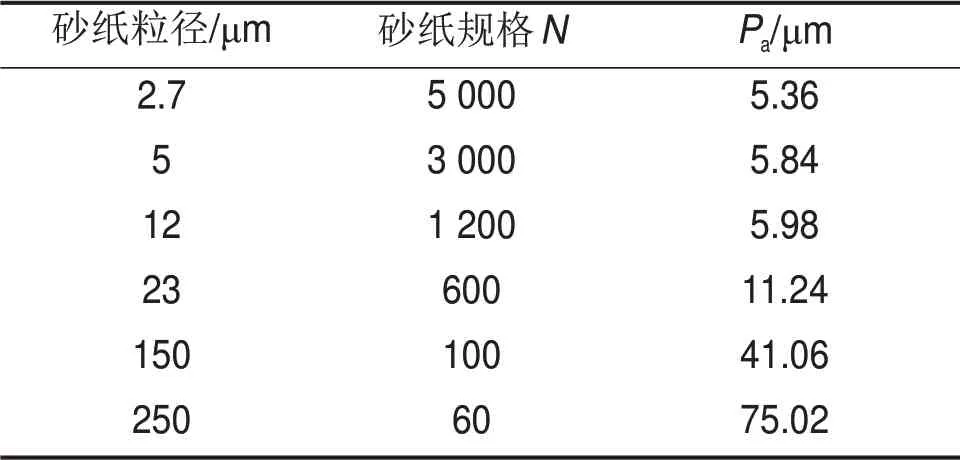
表1 砂纸表面粗糙度指标Table 1 Index of surface roughness of sandpaper

鉴于砂纸规格N与粗糙度指标数值相差较大，函数关系不明显，故先将测试数据进行对数化处理，然后采用最小二乘法对砂纸规格与结构表层粗糙度指标Pa的关系进行拟合，可获得图1所示的关系曲线，曲线拟合系数R2大于0.98，相关性较好。由此，可建立砂纸规格N与结构表层粗糙度指标Pa的指数化拟合公式：

式中：lnPa为结构表层粗糙度指标的对数，μm；lnN为砂纸规格的对数；A和B为常数，可根据结构表层粗糙度指标测量数据拟合得到，本文分别取值为29.117和-1.356。

从图1可知：结构表层粗糙度随着砂纸规格的增大而近似成指数函数衰减，当砂纸规格为100时，由式(1)换算得到粗糙度指标Pa为39.29 μm 与表1中实测数据相差4.31%；同时砂纸规格与粗糙度的关系曲线符合砂纸规格愈大，粗糙度越小的规律，本文拟合的经验公式是合理可行的。

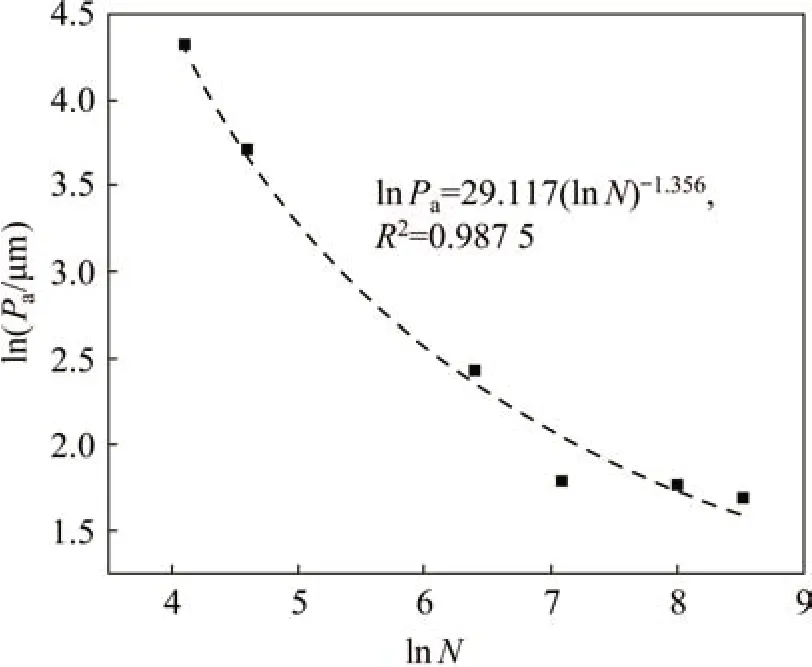
图1 砂纸规格与粗糙度关系曲线Fig.1 Relation curve of sandpaper mesh number and roughness

因此，由施工控制条件、气候等其他因素在混凝土桩基、挡土墙等结构表层形成的粗糙度，可通过本文建立的指数化拟合公式，与砂纸规格建立一一对应关系，以此表征结构表层的粗糙度，采用不同规格的砂纸即可模拟出混凝土结构物表层粗糙度的变化，并实现结构表层粗糙度的定量换算，为开展考虑结构物表层粗糙度的相关试验模拟和研究提供了有益的参考。

2 混凝土-黏土接触面直剪试验

2.1 试验仪器

试验采用ZJ 型应变控制式直剪仪，该剪切仪上、下剪切盒尺寸相同，其内部可容纳横截面积为30 cm2，高为1 cm 的试样。该仪器通过驱动下剪切盒产生水平位移进行剪切，可以在不同垂直压力荷载(50，100，200，300和400 kPa)下施加剪切力同时剪切4个土样。通过显示屏中读出剪切位移值，同时利用电测百分表测得量力环变形，根据量力环系数，可以求出水平剪应力。该仪器试验效率高，易于控制。

2.2 试验材料及方案

土体材料为长沙地区某单位宿舍楼基坑土，通过土工试验测得该黏土物理性质如表2所示。为避免土样离散性对试验结果造成不良影响，本试验采用重塑土样，参照标准[21]配置，将经过烘干、粉碎、过2 mm筛等程序得到的干燥土样，按含水率为24%配置好后，放置1～2 d，以保证水分均匀。利用实验室与直剪仪上下盒半径相同的环刀制作圆柱状土样，同时为了避免试样密实度的差异对试验结果产生不利影响，因此，对土样进行分层击实，每次击实次数相同。

表2 黏土物理力学参数Table 2 Physical and mechanics parameters of clay

鉴于混凝土桩-黏土接触面的微观尺寸特性，若采用大比例或足尺桩基进行模拟，接触面处的荷载施加或数据采集难以保证质量，且考虑到试验过程中混凝土试样主要承受压应力，因此采用与混凝土抗压性能较接近的标准透水石试件模拟混凝土桩。

本次试验采用规格为120，320 和600 的砂纸，通过式(1)实现对接触面表层的粗糙度模拟和量化，分别模拟粗糙度Pa为10.46，14.90和32.43 μm时混凝土桩-黏土界面的接触面表层粗糙度。试验时为避免透水石与砂纸之间产生剪切滑移，采用氰基强力胶将砂纸黏结在透水石一侧，然后将土样和透水石分别置于直剪仪的上盒和下盒，上盒固定不动，通过移动下盒形成剪切，剪切速率为0.8 mm/min，如图2所示。本试验根据表层粗糙度的不同分为3组试验，每组试验包含100，200和300 kPa 这3 个工况，每个工况剪切3 个试样，试验结果取3个试样的平均值。

图2 试件及加载示意图Fig.2 Test piece and loading diagram

3 试验结果与分析

3.1 剪切应力-剪切位移曲线

接触面粗糙度Pa分别为10.46，14.90 和32.43 μm 时，不同法向应力下，混凝土桩-黏土接触面剪切应力-剪切位移曲线如图3所示。

从图3可知：1)在相同粗糙度条件下，接触面剪切强度随着法向应力增大而增大。当粗糙度为32.43 μm时，对于法向应力为100，200 和300 kPa时的接触面抗剪强度分别为69.48，109.28 和143.20 kPa。2)在相同粗糙度条件下，接触面极限剪切位移值随着法向应力的增大而增大，但变化幅度不大，在0.3～0.4 mm 之间。3)在不同法向应力下，接触面剪切应力-剪切位移曲线变化趋势一致。但法向应力达到300 kPa 时，在剪切应力-剪切位移曲线转折点之后，剪应力并未趋近于定值，而具有一定的斜率。该现象表明，当法向应力达到一定界限时，混凝土桩-黏土接触面处发生剪切破坏后，土体本身仍继续发生小幅度剪切变形，呈现出典型的弹塑性变形。

当法向应力σn分别为100，200 和300 kPa 时，不同粗糙度接触面的混凝土桩-黏土接触面剪切应力-剪切位移曲线如图4所示。

从图4可知：1)接触面抗剪强度峰值随着粗糙度的增大而增大，同时伴随着法向应力的增大，粗糙度对抗剪强度的影响呈现减弱趋势，例如：粗糙度为32.43 μm 时与14.90 μm 时相比，在法向应力为100，200和300 kPa时，接触面抗剪强度增长幅度依次减少为16.85%，15.95%和9.96%。2)在相同法向应力条件下，接触面极限位移值随着粗糙度的增大而增大。3)不同粗糙度的接触面剪切应力-剪切位移曲线均存在一个基本重合段，但随着剪切位移的增大而逐渐分化出去。这可能是由于试件表面凹凸几何尺寸与黏土颗粒较为接近，初始状态下黏土颗粒与接触面咬合充分，接触面抗滑移摩擦强度大于土体内部剪切应力，此时剪切位移主要为接触面附近土体内部的剪切变形，而混凝土桩-黏土接触面之间相对剪切位移很小，也间接表明接触面具有一定厚度；当剪切应力逐渐增大并超过接触面抗滑移摩擦强度后，接触面产生相对剪切位移，此时剪切变形主要为接触面剪切滑移产生的位移。

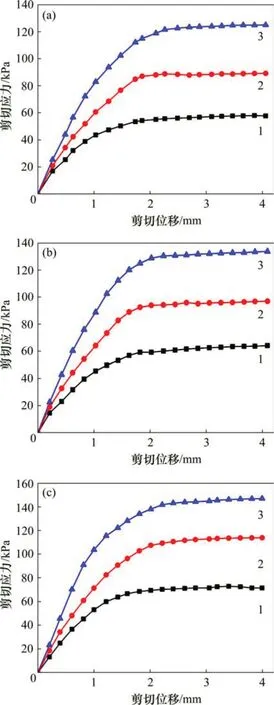
图3 不同法向应力下剪切应力-剪切位移曲线Fig.3 Shear stress-shear displacement curves under different normal stresses

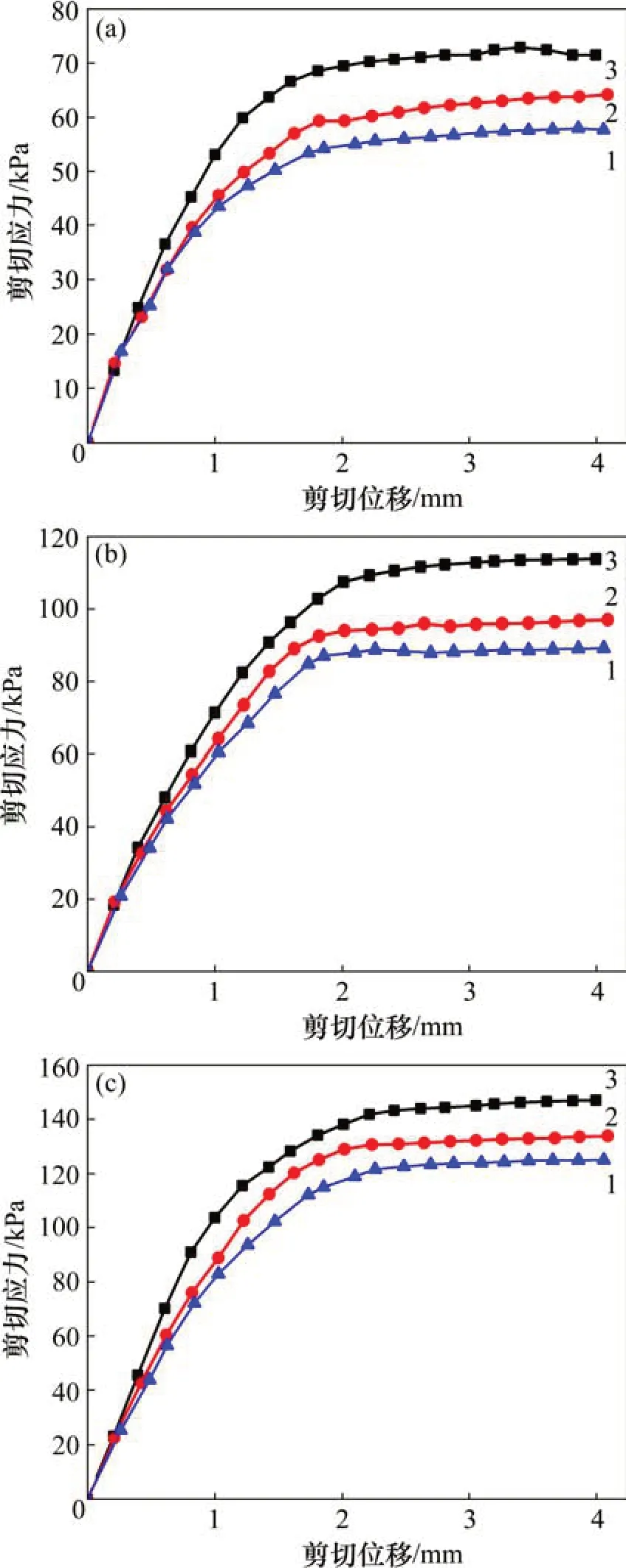
图4 不同粗糙度下剪切应力-剪切位移曲线Fig.4 Shear stress-shear displacement curve under different roughnesses

3.2 接触面抗剪强度

当法向应力分别为100，200和300 kPa时，不同粗糙度条件下混凝土桩-黏土接触面抗剪强度如表3所示。

基于表3的试验结果，采用最小二乘法拟合得到接触面抗剪强度与粗糙度的关系如图5所示。拟合曲线的相关系数R2均大于0.93，拟合度较高，接触面表层粗糙度与抗剪强度的拟合方程可表示为

式中：τp为接触面抗剪强度，kPa；Pa为接触面表层粗糙度，μm；C和D为经验系数，通过试验数据回归获取。

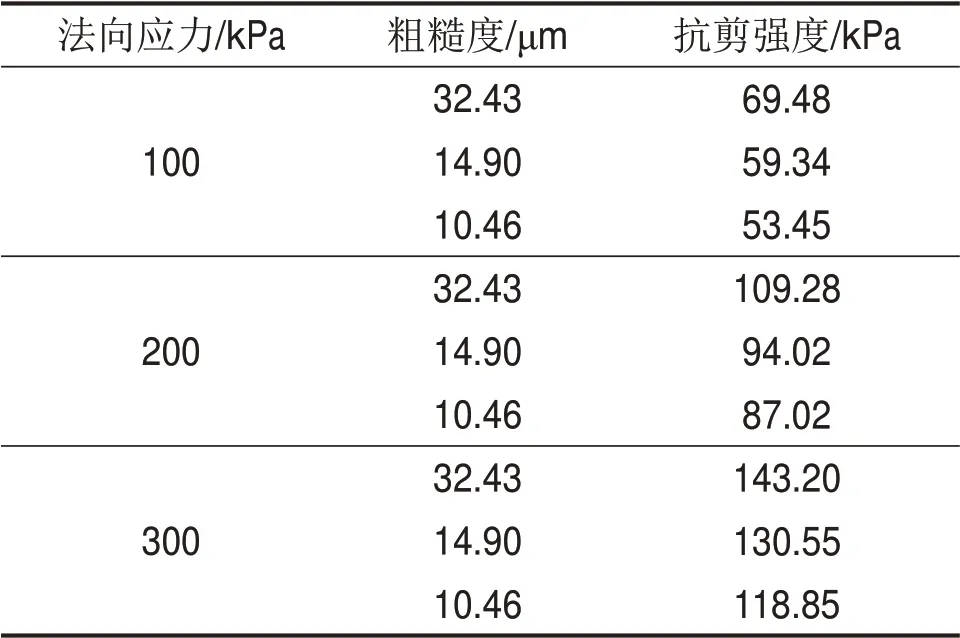
表3 不同粗糙度下接触面抗剪强度Table 3 Shear strength of interface with different roughnesses

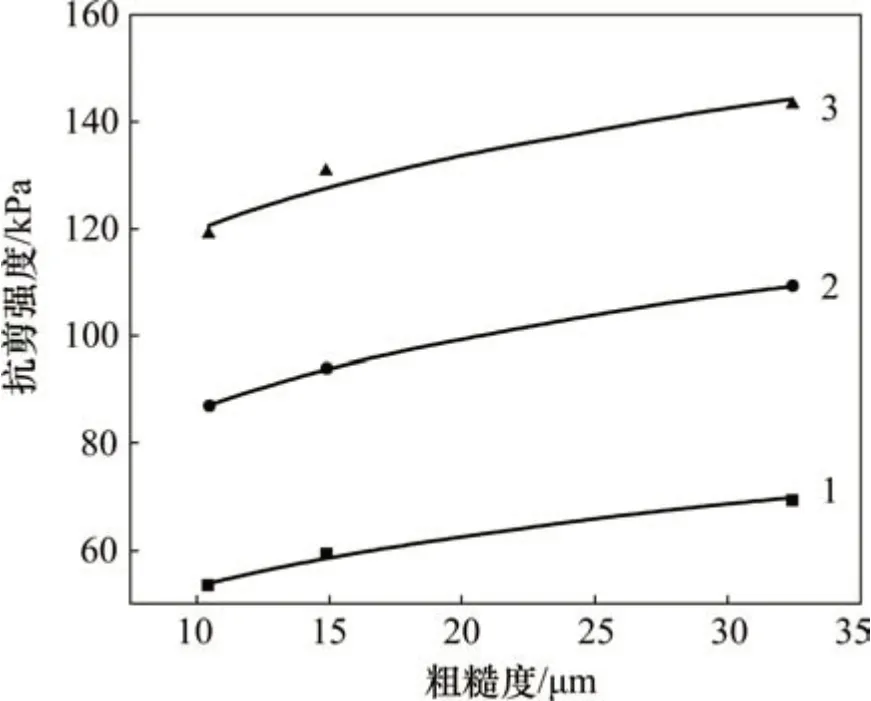
图5 抗剪强度与粗糙度的关系Fig.5 Relationship between shear strength and roughness

由图5可知：同一法向应力下，接触面抗剪强度随着粗糙度的增大而近似幂函数关系增长，且拟合函数的指数C都是大于0 且小于1 的数。表明接触面抗剪强度的增长速率随粗糙度的增大而减小，粗糙度存在临界值，当粗糙度达到临界值后，抗剪强度不再随着粗糙度的增加而显著增大，而是趋近于定值。

3.3 接触面抗剪强度参数

文献[9,14]研究表明：混凝土桩-黏土接触面抗剪强度服从莫尔-库仑准则，可以使用黏聚力c和内摩擦角ϕ表示。因此，基于最小二乘法对不同粗糙度下接触面剪切强度与法向应力进行线性拟合，结果如图6所示。

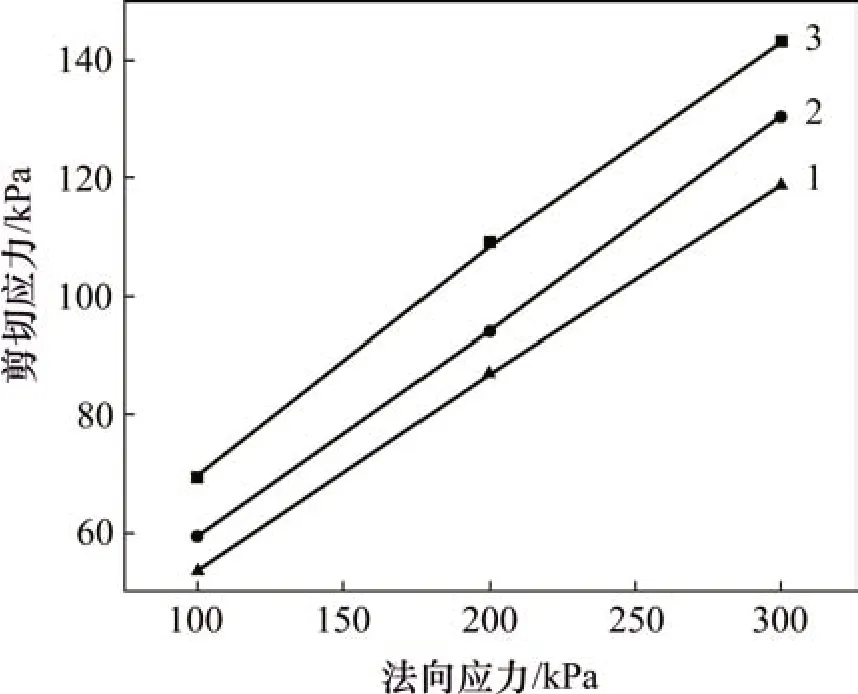
图6 不同粗糙度的接触面抗剪强度Fig.6 Shear strength of interface with different roughnesses

由图6可知：同一粗糙度条件下，接触面抗剪强度随着法向应力增大而增大，二者近似呈线性关系，拟合的相关性系数R2在0.99 以上，因此，本次试验也验证了接触面时剪切破坏服从莫尔-库仑破坏准则。线性拟合得到不同粗糙度下接触面抗剪强度参数，如表4所示。

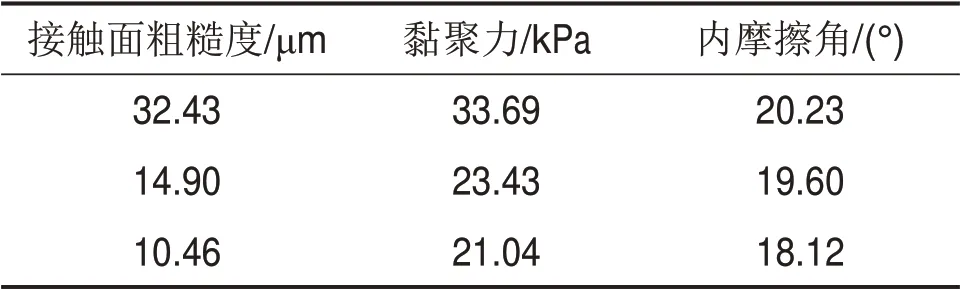
表4 接触面抗剪强度参数Table 4 Shear strength parameters of interface

由表4可知：黏聚力与内摩擦均随着接触面粗糙度的增大而增大，但均小于黏性土自身力学参数。结合图4的分析结果可知：在现有试验条件下，剪切破坏为混凝土桩-黏土接触面间的剪切滑移破坏。

4 结论

1)基于指数化拟合公式对接触面表层粗糙度进行模拟，实现了结构表层粗糙度的定量换算，为开展考虑结构物表层粗糙度的相关试验模拟和研究提供了有益的参考。

2)接触面抗剪强度随着法向应力增加而呈线性关系增大，符合莫尔-库仑破坏准则，且在现有试验条件下，混凝土桩-黏土接触面的剪切破坏形式表现为接触面滑移破坏。

3)混凝土桩-黏土接触面处的剪切破坏过程可分为“土体弹性剪切变形—接触面剪切滑移—土体弹塑性剪切变形”3个阶段，即：初期剪切变形主要表现为接触面厚度范围内的土体内部剪切变形；当剪切应力逐渐增大并超过接触面抗滑移摩擦强度后，剪切变形主要为接触面产生相对剪切位移和滑动；当法向应力达到一定值时，接触面剪切破坏后土体自身继续产生小幅度剪切变形，表现出典型的弹塑性变形。

4)接触面抗剪强度随粗糙度的增加而呈幂函数关系增大，但随着法向应力的增大，粗糙度对抗剪强度的影响呈现减弱趋势，即粗糙度存在临界值。

5)本文采用不同规格砂纸来模拟不同粗糙度的桩表面，并未考虑接触面的剪切刚度与桩身混凝土剪切刚度的不同，下一步将开展剪切刚度的差异性对于界面特性的研究。