基于航空的复合材料与金属连接结构的拉伸性能及渐进损害研究

袁 媛

（西安航空职业技术学院，陕西 西安 710089）

与传统金属材料比较分析，复合材料具有其自身的独特优势，即比强与比模较高、耐疲劳、耐腐蚀，且具备向异性与可扩展性等，其在推动航空航天设备轻量化与高性能提升等方面发挥着重要作用。复合材料的应用势必会与金属异质材料相衔接，尤其是在航空领域中，翼梁缘条、桁条等存在复合材料于金属件的相互连接[1]。传统复合材料和金属之间的连接有机械连接、胶接、混合连接三种工艺。其中机械连接对于环境的适应能力非常强，且具备较好的可靠性，但是其孔边应力太过集中，重量也太大。胶接技术能够切实实现不同性质材料的连接，而且其质量较轻、应力分布比较均匀，还具有良好的耐疲劳性。但是，同时也具备一定的缺陷，即力学性能太过分散，难以适应湿热环境，可靠性明显不足等。而混合连接能够有效避免其两者的不足，并将其优点充分发挥出来，可紧固件的利用在一定程度上提高了成本，加大了质量，从而使得复合材料所具备的减重优势被抵消[2]。

1 ANSYS复合材料单元

1.1 复合材料单元

复合材料结构理论主要包含等效单层二维理论、分层理论、三维理论，其中，有限单元与之相对应，包括层合单元、多层单元、三维固体单元。其中，层合单元在结构厚度材料性能变化的影响下，实现了等效均衡，并进一步实现了有限元模型的简化，其一般用于复合材料结构振动与屈曲分析。多层单元的每层材料铺层都会被处理成二维层，以此仿真模拟。并沿厚度方向集中铺层加以计算分析，其主要用来进行应力与失效分析。在具体结构中，复合材料结构一般是由多层材料铺层，使用多层单元进行模拟，必须对每层材料铺层通过二维层加以仿真。所以有限元模型相对复杂，基于计算模型，自由度会不断增长，以此对软件分析效率与水平造成影响，急需计算机资源。三维固体单元对材料性能在厚度变化影响下不需要进行特殊设定。复合材料结构的各个铺层都会单独看作是独立三维体实现数值模拟。因为复合材料的铺层尺度比较小，在有限元模型中，需要具备精细化单元网格，这样的话，计算机资源需求必然会随之扩大，从而使得复合材料的有限元分析与实际情况出现严重分离现象[3]。对此在详细分析复合材料时，通过多层单元和三维固体单元实现仿真模拟，并不可取。现阶段有限元分析软件主要利用的是层合单元，在分析时使用层合单元进行分析，并在后处理之后获得应力分析结果。ANSYS分析也不例外，主要是通过层合单元实现复合材料建模，进而便可以进一步分析各种不同类型的结构。

1.2 复合材料各向异性特点

通过单向预浸带进行多层铺设然后加以固化，形成层压结构，这是目前航空领域复合材料结构的主要形式。其中，单向预浸带具有较强的正交异性，能够在各个方向铺设相应比例的单向带，从而满足结构平面的方向性要求。而层压结构不仅要具备向同性，还要具备向异性。而各向异性在很大程度上加大了结构设计与制造的难度。复合材料结构设计主要包含两层次，且彼此有机联系，也就是复合材料层压板与结构设计。另外，复合材料层压结构各向异性的层间性能明显要比内部性能较差，组分材料纤维与基体力学性能之间的差异十分显著，导致复合材料层压结构破坏机制和金属结构之间完全不同，因此必须在进行结构设计时必须充分考虑冲击损伤与分层[4]。

2 复合材料与金属连接结构的拉伸性能影响因素

2.1 翻 边

没有翻边的复合材料与金属连接结构有限元模型，在去除翻边之后，其他和存在翻边的结构完全一致。而没有翻边的复合材料与金属连接结构在发生损伤时，其荷载相对存在翻边的结构要高一些。在出现损伤之后，没有翻边的结构因为层合板端头已经有所损伤，此时刚度下降速度要明显较快，层合板孔边挤压纤维发生断裂的初始荷载相对较低，而最终拉伸强度也比较低。因为没有翻边的结构端局直径相对要小，所以，其是层合板端头纤维断裂和分层破坏，也就是所谓的端头断裂，所以说，翻边能够显著提高复合材料与金属连接结构拉伸强度。

2.2 胶层韧性

脆性胶层可以使用线弹性材料进行仿真，韧性胶层则需要使用折线进行仿真。韧性胶层和脆性胶层之间存在较大差异，不同的韧性胶层连接结构拉伸性能基本上相一致，韧性胶层结构的破坏荷载明显要比脆性胶层结构要高。

2.3 接触面摩擦系数影响

复合材料与金属连接结构的层合板孔与金属件会产生一定的摩擦，系数越大，那么拉伸后续结构刚度就越高，最终破坏荷载也会越大[5]。

3 计算模型

3.1 几何模型

想要实现双向拉伸模型构建目标，必须积极关注单向拉伸界面剪力与剪切面面积之间的关系。虽然单向拉伸界面剪力受剪切面面积影响，但是双向拉伸界面剪切力却不受其影响。构建双向拉伸试验模型，为探究双向拉伸界面应力提供帮助[6]。实验模型具体如图1所示。

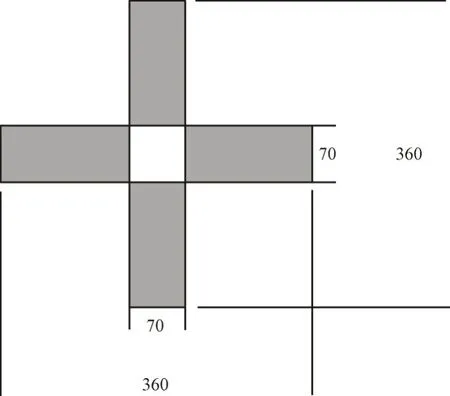
图1 双向拉伸试样图

如果模型基于构件段获取，材料参数与复合参数的铺层角度、构件参数相一致，而材料参数与铺层厚度相关参数具体如表1所示。

表1 材料与铺层参数

3.2 有限元模型

在ANSYS有限元中进行建模，采用八节点三维层状体单元Solid46进行复合材料层合板仿真模拟，并利用Solid45进行铝合金、高锁螺栓模拟。同时，还需要针对网格局部进行精细化，以此保证螺栓孔应力与应变分布的精确性。如果高锁螺栓和符合材料层合板、铝合金板的连接，属于无缝配合，那么复合材料与金属连接构件的螺栓孔壁在高锁螺栓的作用下，会渐渐变形，而且螺栓在拉伸载荷与剪力载荷的共同挤压下也会变形。为了对高度非线性接触行为进行仿真模拟，通过ANSYS有限元软件的面面接触单元，进行接触对定义[7]。

3.3 失效准则

因为有限元模型单元在失效之前与失效之后的应力变化幅度太过明显，应变变化却十分平缓，所以，为了对复合材料与金属连接结构的拉伸损伤进行判别，在累积损伤模型中，基于Hashin准则与Ye分层准则为依据进行失效判断，就应力与应变关系，转换应力失效准则为应变失效准则，以此预测失效并加以分析[8]。设定复合材料单层弹性常数不会受到层合板邻层的作用，那么其主方向应力与应变关系为

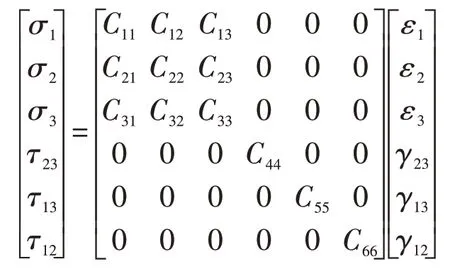
式中：σ为拉伸强度，τ为剪切强度，ε为拉伸应变，γ为剪切应变，Cij为刚度系数。而标号纤维的轴向、横向、单层板法向。

构建以应变描述为载体的失效准则，纤维拉伸失效、压缩失效；基体拉伸与剪切失效、压缩与剪切失效；分层失效准则为

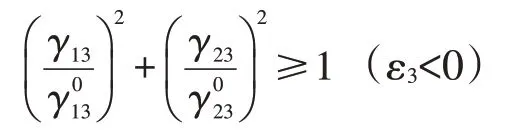
式中：ε11、ε22、ε33为应变；T与C为拉伸与压缩为剪切应变。

3.4 性能退化准则

在复合材料层合板需要承受外部乘加的载荷时，结构内部单元应力与应变满足任何失效准则的时候，可以判定为单元失效，则应对其材料性能做一定的退化处理。而在损伤中材料性能出现退化，则可以采用相应的退化模型[9]。其中优化Camanho 模型，获得性能退化准则为：

3.4.1 纤维拉伸失效

设定此单元无法承担载荷，弹性模量1，剪切模量12、13，泊松比12、13退化到初始状态值的大约1%，弹性模量2、3，剪切模量23，泊松比23退化到初始状态值的大约6%。

3.4.2 纤维压缩失效

设定此单元难以承受载荷，弹性模量1，剪切模量12、13，泊松比12、13退化到初始状态值的大约2%，弹性模量2、3，剪切模量23，泊松比23退化到初始状态值的大约12%。

3.4.3 基体拉伸与剪切失效

弹性模量2，泊松比12 退化到初始状态值的大约1%，剪切模量12、23，泊松比23 退化到初始状态值的大约10%。

3.4.4 基体压缩与剪切失效

弹性模量2，泊松比12 退化到初始状态值的大约2%，剪切模量12、23，泊松比23 退化到初始状态值的大约20%。

3.4.5 分层失效

弹性模量3，剪切模量13、23，泊松比13、23退化到初始状态值的大约2%。

损伤机制之间是相互联系的，其中任何类型损伤都会引发其他损伤。而含有多种损伤类型的部分区域，应该利用损伤类型材料退化方法实现融合。

3.5 累积损伤

在有限元模型中添加初始荷载的时候，基于失效准则判断复合材料。未发生失效，就继续增加载荷。发生失效，则针对失效单元遵循性能退化准则加以处理，并重新计算与分析。对此过程进行循环，直到负荷材料结构全面损坏。想要直观展示复合材料层合板失效的具体部位，在有限元程序的后处理中，不需要再展示失效单元。针对复合材料与金属连接结构，进行损伤累积数值计算分析，获取层合板在载荷不断增加的影响下造成的损伤叠加过程[10]。在逐渐增加静拉伸载荷的时候，复合材料与金属连接结构严重损伤，具体区域为层合板接头螺栓安装孔受到挤压的位置开始。在初始破坏载荷模拟值接近静拉伸试验实验结果的时候，误差则非常小。而载荷不断增加，层合板损伤渐渐累积，沿着螺栓挤压的方向进一步扩散。在增加载荷之后，损伤则会快速扩散，那么失效单元也会逐渐增多。在载荷增加到一定程度的时候，层合板损伤区域扩散到复合材料与金属相连接的结构端部，从而使得结构连接件的承载能力严重损失，进而破坏载荷，模拟结果比静拉伸试验测试的载荷结果要高，而层合板损伤位置恰好与试验结果相吻合。

4 结 论

总之，复合材料与金属连接结构在比较小的拉伸载荷下，应变会随着载荷不断增加呈现线性趋势也随之增大，在拉伸载荷增大之后，应变和载荷呈现非线性变化。其中，在金属上的应变明显要大。而通过仿真模拟，复合材料与金属连接结构的初始破坏载荷接近静拉伸试验载荷。损伤则是产生于复合材料接头螺栓安装孔受到挤压的位置，并在载荷不断增加的作用下，损伤累积，沿着螺栓的挤压方向随之扩散，连接结构受到挤压损坏，与试验结果相一致。