试论航空发动机涡轮机匣传热分析技术

权少宁

（西安航空职业技术学院，陕西 西安 710089）

航空发动机涡轮机匣能够有效控制叶尖间隙，在进行发动机设计时，准确预测运转温度，获取涡轮机匣在各种状态下的变形量，能够有效帮助叶尖间隙控制系统开发。涡轮机匣是热端部件，结构十分复杂，包括各种各样的流动形式，即平板、凹槽、冲击、多孔阵列等等，换热规律也比较复杂。而因为涡轮机匣的工作环境温度比较高，流动形式太过多元化，在温度分析时，换热模型实际上与具体结构存在明显差异，从而使得难以预测机匣温度与变形，进而不能确保叶尖间隙控制。因此，为了涡轮机匣温度分析的准确性得到提升，应进一步深入探究涡轮机匣表面换热规律[1]。

1 航空发动机涡轮机匣传热分析技术环节

基于高压涡轮机匣进行传热分析，其流动传热分析过程比较繁杂，受各种因素影响，但是本质上是流体动力、热交换理论、发动机部件的有机结合。流动特性是对发动机二次流空气的运行状态进行探究，换热特性是对发动机零件表面与气流热交换原理进行探究。流动换热的关键在于求解流场，现阶段N-S 方程的准确求解依旧是一大难题，需要以实验为载体加以弥补[2]。

充分了解高压涡轮机匣和主动间隙控制系统结构特性，熟练掌握流动传热的影响因素，有助于流动与传热分析模型构建。切实结合二次流空气系统设计，进行一维分析，从而获取涡轮机匣气体流动环境状态。就发动机具体结构与流动状况，就各流动单元进行准则模块化处理，以此构成不同类型节流单元串联、并联相组成的复杂空气系统一维流体计算网络，以进一步做计算分析，进而获取高压涡轮机匣流动特性。在此基础上，对涡轮机匣进行CFD数值仿真研究，探究涡轮机匣流动换热分布的规律性，基于数值仿真验证换热特性。数值仿真有利于获取相关分布规律，但是并未全面实现对机匣流动换热特性的准确分析，其特性的构建需要进行实验验证[3]。就热物理模型与计算获取边界条件而言，基于有限元计算，获得发动机运转时机匣的瞬态温度，有助于叶尖间隙分析和机匣强度设计。

总之，想要获取涡轮机匣温度，切实解决相关问题，关键就在于计算换热边界条件。由于机匣的复杂性，导致难以预测周围流动换热环境。而换热边界准确性在很大程度上影响着机匣温度分析的精确性，因此换热边界条件分析是机匣温度分析的关键，对此，必须健全既有计算方法，以数值仿真与实验分析保障换热边界条件的准确性。

2 涡轮机匣数值仿真分析

高压涡轮机匣内部的构造十分特殊，是一个腔体，其换热备受气流流动影响，因为结构复杂导致无法基于既定准则进行计算。以一维空气系统流动计算的进口压力与质量流量作为边界条件，通过CFD 软件进行数值计算。涡轮机匣流场结构在几何结构影响下，其腔体结构强制内部气流改变方向，以构成气流涡，对壁面产生相应作用，对气流和壁面之间的换热造成直接性影响。通过进气孔流入机匣内部的气流速率非常高，直接冲击着壁面，在冲击区的周围沿着边缘逐渐流动，速率也会随之渐渐降低[4]。冲击孔与涡轮机匣的外壁面区域相对应，存在十分显著的斑状冲击强换热区域，其特性与冲击孔相同，是在剧烈冲击下导致的，也是受空气冷却机匣的作用造成的。

在机匣的内壁上，前部分，受入流孔冲击，换热系数较大，但是冲击区域以外，换热系数会不断缩小，但是减小幅度不断变弱。中间部分，气流和壁面之间的相互作用处于均衡状态下，换热系数的分布也相应的非常均衡，但是比较小。后部分，冲击位置的气流和壁面之间的作用十分强烈，换热比较剧烈，系数也很大，但是冲击区域外，相互作用减小，换热系数也比较小。就数值分析结果可知，腔体内部的气流速度始终处于平衡状态下，壁面换热也比较均衡[5]。总之，孔出流对避免的冲击作用很强，两者之间的换热也比较剧烈，系数较大。涡轮机匣结构多元化，使得气流方向逐渐变化，造成漩涡结构复杂化。气流涡所在位置上，气流和壁面的相互作用比较强烈，换热系数也较大。

3 涡轮机匣换热实验

3.1 装 置

为了降低实验难度，在不对机匣流动换热特性造成影响的基础上，对既有结构进行简化，其中机匣属于环腔结构，受对称性的影响，选取环状机匣具有周期性的1/27 进行深入探究，并简化其内部通道的圆弧面为平面。具体实验装置如图1所示。

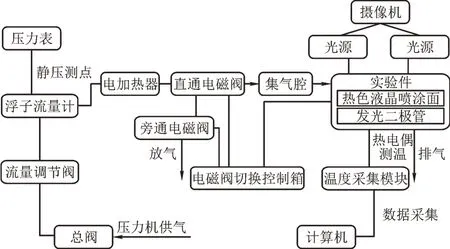
图1 实验装置图

3.2 原 理

基于瞬态法进行机匣传热系数测量，通过加热器进行来流加热，物体与环境、以及热量传递尚未处于稳定状态的时候，应就实验可以获取的温度数据与时间等相关参数，求解传热系数。所以，应充分了解温度数据、时间、传热系数之间的关系。因为实验的时间比较短，加热气流和换热之间导致的实验模型温度随之发生了一定变化，并未受到任何的其他影响，这时实验模型导热问题可以通过一维半无限大导热加以解决。半无限大物体模型具体如图2所示，其从0界面逐渐向正x向与其他坐标延伸。这种物体并不存在，但在非稳态导热的初始阶段，很有可能会把实物看作是半无限大物体，然后进行适当处理。在进行实验时，把加热器接通电源之后，气流的温度会渐渐上升，此时扰流柱通道端壁受热气流加热的影响，其材料是有机玻璃，热扩散率比较低，测量时间较短，温度变化只是停留在表面附近，并没有深入到端壁内部，所以，可以把端壁当作半无限大物体，导热过程为一维，只需要沿厚度传热即可[6-7]。

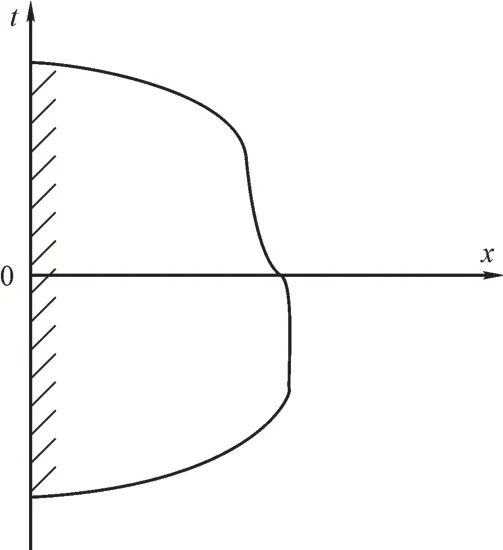
图2 一维半无限大模型

在初始阶段，模型温度之中处于均衡的状态下，并与气流、环境温度之间等同，然后在气流温度上升的时候，气流和壁面进行对流换热，壁面温度逐渐上升，同时朝向模型内进行传热。此过程为

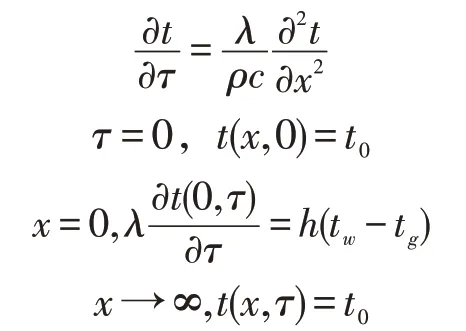
壁面温度为

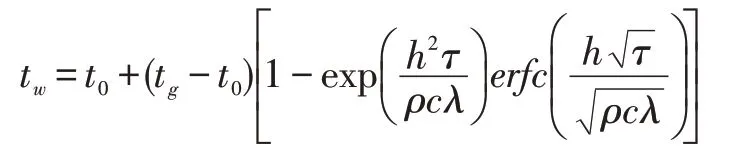
式中：t0为模型与气流初始温度，℃；tw为壁面温度，℃；tg为温度上升之后气流温度，℃；t（x，τ）为τ时模型深度为x的温度，℃；ρ为模型密度，kg/m3；c为比热容，kJ/(kg·℃)；λ为导热系数，W/(m·℃)。

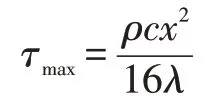
在实验中，端壁非稳态导热边界条件是第三类条件，传热系数是有限值，此时半无限大导热最大时间明显要长于计算时间。就有力玻璃的特性，可知最大时间为195 s。所以，在比最大时间小的状态下，进行端壁温度场测试，可以利用半无限大模型。

3.3 测 量

雷诺数为

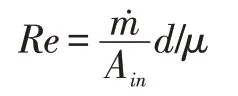
式中：为通过实验段质量流量，kg/s；μ为动力黏度，N·s/m2；Ain代表入口射流孔面积，m2；d为孔径，mm。在实验中，雷诺数为：12×104～20×104。努赛尔数为

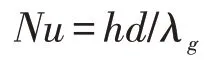
式中：λg为气体导热系数，W/(m·℃)；h为传热系数，W/(m·℃)。

在进行实验的时候，电加热器接通电源之后，气流开始加热，温度逐渐上升，此时应开启旁通电磁阀，并将直通电磁阀及时关闭。通过阀门进行工况调节，从而保证其稳定性和可靠性。在满足工况要求后，及时将电磁阀切换掉，加热气流基于实验件，摄像机也开始运行，详细记录热带偶对气流具体温度的测量。在结束并变色之后，实验结束[8]。摄像机全程记录端壁壁面温度变化中所产生的颜色变化，以及热电偶在气流温度测量中产生的变化。在进行实验时，加热气流基于实验件，壁面受热气流加热，测量时间保持几十秒，可以将端壁作为半无限大物体。测量端壁壁面温度、加热时间、气流温度等在时间推移下呈现上升状态，结合模型物性参数与初始温度，进行传热系数计算。

3.4 结果分析

3.4.1 换热分布

就实验件结构特性，传热系数测量主要分为三大区域，如图3所示，面a、面b、面c。

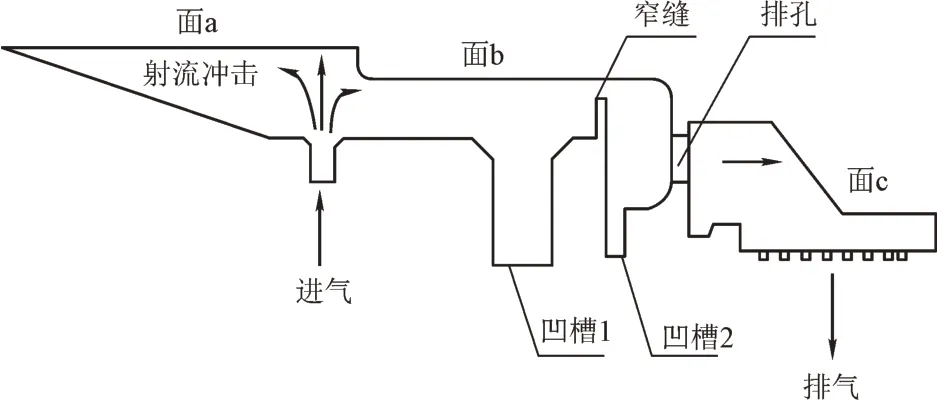
图3 换热测量表面

面a位于腔体前部分，气流通过入口射流孔缓缓进入，对壁面造成一定冲击，在受到阻碍之后，及时改变方向，然后渐渐向下形成回流，流动在射流冲击的限制下进行。就努赛尔数分布可知，面a对应入口所构成的高换热区域，按照从中间向外的顺序，换热呈现减弱趋势。距离冲击区域较远的传热系数较小，尤其是最左端局部壁面换热系数非常小。面b对应腔体后部分，在面b左端所对应的冲击孔传热系数最大。在墙体凹槽位置的换热速度下降非常快，这主要是因为气流下游流动到凹槽位置的时候，会随之形成顺时针的漩涡，速度快速下降，传热系数也随之降低。而在入口窄缝的传热系数却有了一定程度的升高，因此经过窄缝的时候，流动速度提高，传热系数提高。气流进入腔体之后，换热处于均衡状态。面c对应的射流孔冲击区域换热比较强，其中最右侧最弱。面c换热分布受热口射流冲击影响，从射流孔进入冲击斜壁面，周围换热显著较高。但是不同冲击区域换热存在明显差异，其中中间区域在冲击之后反卷的气流发生碰撞，能够强化换热，因此，此区域换热明显比两端区域要高[9]。但是，最中间区域换热与相邻区域换热相比却较低，这是因为入口流速较小。

3.4.2 平均换热

在雷诺数增加的趋势下，各面平均努赛尔数都有所增加，其中，面a换热>面b换热>面c换热。整面努赛尔数在雷诺数增加的趋势下呈现线性增加的趋势。而且在雷诺数增加的影响下，面c 的努赛尔数在雷诺数为200 000 工况的时候，突然增大。这是由于在此工况下，冲击孔所对应高换热区相邻区域内不存在明显的低换热区，冲击孔与中间孔对应的高换热区域几乎呈现相连接的状态[10]。

4 结 论

总之，基于详细分析航空发动机涡轮机匣流动换热与温度，掌握机匣流动换热规律，构建涡轮机匣传热分析技术体系。通过进行流动换热CFD 数值仿真与换热实验，获得换热分布特征。而且，冲击孔出流强烈冲击了壁面，在冲击区域换热很高，部分系数也比较大。由于涡轮机匣的内部结构十分复杂，气流方向一直在变化，从而构成了繁杂的漩涡结构。在存在气流涡时，气流和壁面之间的相互作用比较强大，壁面部分区域的换热系数很大。另外，在雷诺数不断增加的趋势下，壁面的平均换热系数也按照一定顺序在逐渐增大。通过以上研究成果，不仅可以准确分析机匣温度，还能够进一步健全优化传热设计。