翻开中考试卷，感悟学科素养——由一道中考压轴题引发的思考

江苏省扬州市邗江区汊河中学 张定成

江苏省中考已经落幕，翻开各地市的中考试卷，命题精彩纷呈，这都是各地的有关专家集体智慧的结晶，在对试题进行赏析之余，也领悟到了中考相关试题的内涵，更精准地对中考试题进行研究.的确，江苏省各地市的数学中考中，数学压轴题变得越来越能体现学科素养.然而，初中生的思维能力和逻辑推理能力水平是一定的，教学不可能年年都可以提升学生思维的敏捷性，这就造成了学生对压轴试题的求解感到茫然.为此，笔者在翻阅了苏州市中考数学试卷后，对压轴题进行具体分析和思考，将感悟流于笔端，期望在今后的教学实践中激发学生的数学探究欲望，并借此机会搭建一个新课改背景下对数学进行研讨的平台.

一、拜读经典，寻找压轴试题的学科素养

打开江苏省苏州市的数学中考试卷，试题既保持了各地市的统一难度，也体现了近年来试题的连续性，同时更多的是在知识载体不变的情况下考查的方式让人耳目一新.

典例：已知矩形ABCD中AB=5cm，点P为对角线AC上一点，且cm.如图1，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）.设动点M的运动时间为t（s），△APM的面积为S（cm2）.S与t的函数关系如图2所示.

（1）直接写出动点M的运动速度为_________cm/s，BC的长度为________cm.

（2）如图3，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）.已知两动点M、N经过时间x（s）在线段BC上相遇（不包含点C），动点M、N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2）、S2（cm2）.

①求动点N的运动速度v（cm/s）的取值范围.

②试探究S1、S2是否存在最大值.若存在，求出S1·S2的最大值，并确定运动时间x的值；若不存在，请说明理由.

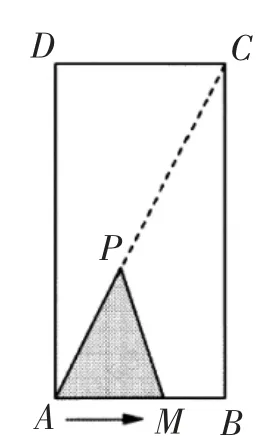
图1

图2

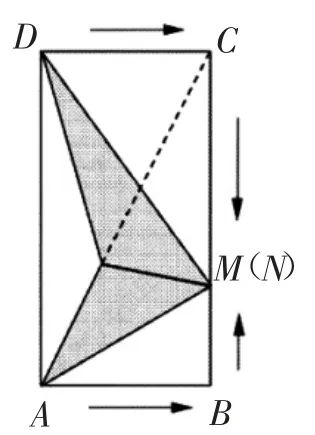
图3

试题分析：（1）在图1中，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C），其运动过程有一个折点B；而图2表示的是△APM的面积S（cm2）与t（s）的函数关系，先增大而后减小，最大值应该在点运动到点B时取得，故动点M的运动速度为=2（cm/s），BC的长度为（7.5-2.5）×2=10（cm）.

感悟反思：动点M在运动过程中构成的函数最值一定是在折点处，不需要先写出函数表达式再进行证明.假设、猜想建立在科学的观察的基础上，世界上没有无缘无故的爱，这是自然学科的基本素养.

（2）①因为动点M、N相遇后停止运动，所以，两动点运动的距离之和为AB+BC+DC=20（cm）.

再根据动点M、N的运动速度分别是2cm/s、vcm/s，同时，两个动点的运动时间都是xs，可以列出方程式2x+vx=20，即v+2=

由题干可知动点M、N在线段BC上相遇（不包含点C），判断5≤2x＜15，解得

感悟反思：本小题以相遇问题为载体，考查了不等式的解法，尤其是将代入中，要注意不等号的变化，这是学生最容易忽视的地方.数学学科的素养在于对运算过程的精准掌握.

②（方法1）过点P作PQ⊥AD于点Q，PH⊥BC于点H.

PQ⊥AD，∠ADC=90°，根据平行线的性质得出PQ∥CD，于是由对应边成比例得到.则PQ=2，AQ=4，进而得到PH=3，DQ=6.

动点M、N在线段BC上相遇（不包含点C），则：

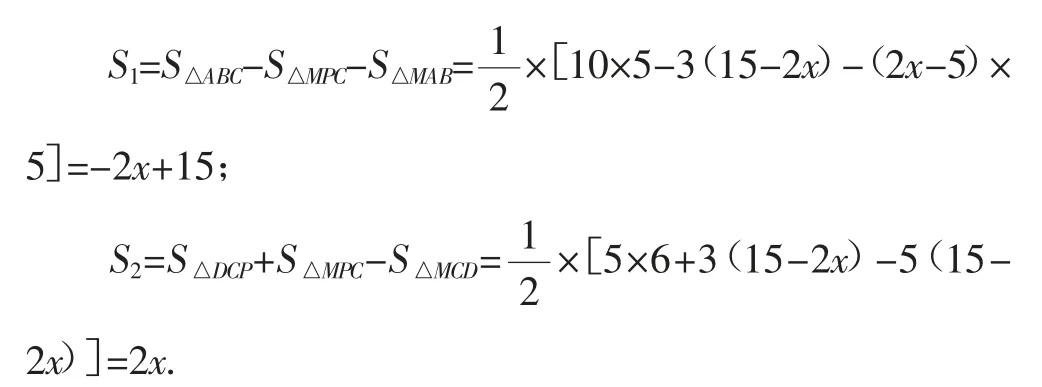
于是有：S1·S2=（-2x+15）×2x，所以，当-2x+15=2x，即时，S1·S2有最大值

（方法2）过点P作PQ⊥AD于点Q，PH⊥BC于点H.

可知AD=10（略去单位，下同），CD=5，得到AC=5

PQ⊥AD，∠ADC=90°，根据平行线的性质得出PQ∥CD，于是由对应边成比例得到.则PQ=2.

动点M、N在线段BC上相遇（不包含点C），则S1+S2=，故S2=15-S1.

S1·S2=（15-S1）×S1，当15-S1=S1，即S1=时，S1·S2有最大值

感悟反思：本小题以求三角形面积和的最值为出发点，考查三角形面积的求解方法和求二次函数的最值的方法，方法是多种多样的，学生可以自由选择.在这里，二次函数的最值是当分解成两个因式（或因数），两个因式（或因数）相等时，其因式（或因数）的积最大，这使试题解析更加简便.这正是数学发散思维的核心素养的运用.

二、思考经典，反思压轴试题的学科素养

通过以上中考中压轴试题的案例分析，得出要求学生综合能力强，数学压轴试题尽显学科素养.这就要求在中考备考中，让学生无所畏惧，压轴试题也是常规试题，只不过综合性较强，所要解答的问题也是循序渐进的.本案例给出的苏州市中考试题，通过对下一届部分学生进行问卷调查发现，基本上都可以得到5分以上的分数.所以，作为一线教师，在今后的教育教学实践中，必须扎实、稳定地进行素质教育，体现以学生发展为基础的教育性理念，“教师下题海，学生上题舟”，减轻学业上的负担，在注重基础的教学上选择一些针对性的训练，让学生自主掌控相关的数学概念，达到新课标的基本标准.

另一方面，本案例不仅是对学生进行运算能力上的考查，也是对他们的思维能力进行考查，尤其是对数学运算灵活性和释疑问题的能力进行考查，充分说明了数学学科核心素养的重要性.因此，在今后的课堂实践中，要以灵活性、理解力的培养为关键环节，设计出一些有针对性的问题，少做一些烦琐的题目.针对性练习题的立意要新，旨在发展学生的创新意识和发散能力.只有这样才能提升学生的综合素养.

一道试题只能是管中窥豹，但是对试题的再次分析、研究，使笔者悟出有必要对中考压轴试题的创新精神进行推广.也希望能同更多的同人一起挖掘出2019年各地市中考题的创新点，回放压轴题设计过程中立意的新颖点、能力的精彩点.