分解构图揭示结构：让新定义题思维可见——以中考新定义考题教学为例

江苏省如皋市搬经镇常青初级中学 夏茂红

中考新定义考题是近年来热点题型，各地在复习备考过程中都会增加课时进行复习应对，但有时新定义选题杂乱，同一节课所选新定义之间关联不紧，影响了复习目标的达成，不利于学生对同一类型新定义问题的深刻理解.笔者最近有机会开设一节新定义专题复习课，精心选取了两道结构近似的新定义考题，引导学生层层递进，发现新定义的本质结构，取得了较好的教学效果，本文梳理该课的教学过程，供研讨.

一、新定义专题复习课的教学记录

例1在平面直角坐标系xOy中，点P到封闭图形W的“极化距离”D（P，W）定义如下：

任取图形W上一点Q，记PQ长度的最大值为M，最小值为m（若点P与Q重合，则PQ=0），则“极化距离”D（P，W）=M-m.

（1）如图1，正方形ABCD以原点O为中心，点A的坐标为（3，3）.

①点O到线段AB的“极化距离”D（O，AB）=_______，点K（5，3）到线段AB的“极化距离”D（K，AB）=_______.

②记正方形ABCD为图形W，点P在y轴上，且D（P，W）=3，求点P的坐标.

（2）图形W为圆心T在x轴上、半径为4的圆，直线y=x+1与x轴、y轴分别交于F、G两点，若线段FG上任一点P都满足2＜D（P，W）＜6，试探究圆心T的横坐标t的取值范围.

图1

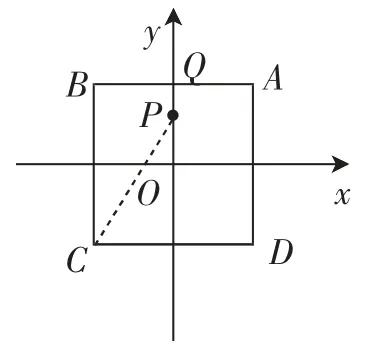
图2

教学记录：第（1）问比较简单，只要对照新定义，不难得出答案.①3-3，6.②先排除点P在正方形ABCD外部的情况，接着设点P（0，y），如图2，由新定义，可连接PC，极化距离是PC-PQ，根据勾股定理，PC=.又PC=PQ+3=6-y，于是可得方程解得y=1.于是根据对称性，可确认点P为（0，1）或（0，-1）.

（2）学生普遍感觉无从下手，找不到解题出发点.教学时我们先引导学生想清条件“线段FG上任一点P都满足2＜D（P，W）＜6”，分开思考“2＜D（P，W）＜6”这个条件如何理解，在半径为4的圆内部，哪个区域内的点满足呢？等到学生想清，原来是以T为圆心，半径分别为1和3的同心圆组成的圆环内部所有点都是满足条件的点，于是可以构造图形分析（如图3～6），这个圆环与线段FG有公共点时，就是符合要求的.于是可分析出相应的圆T的圆心的横坐标的范围是

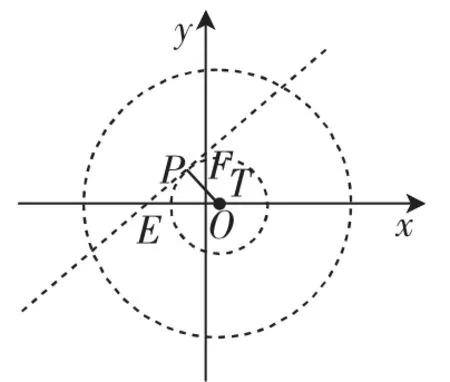
图3

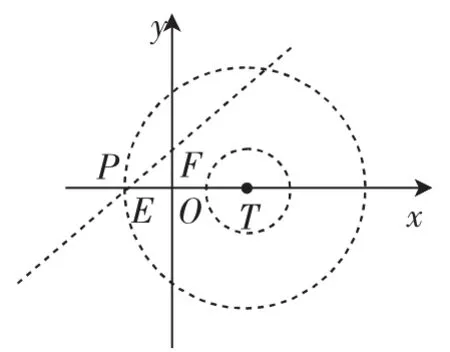
图4

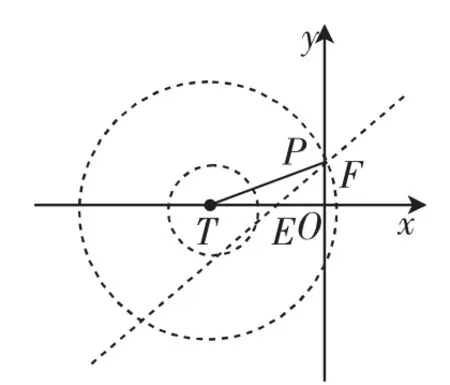
图5

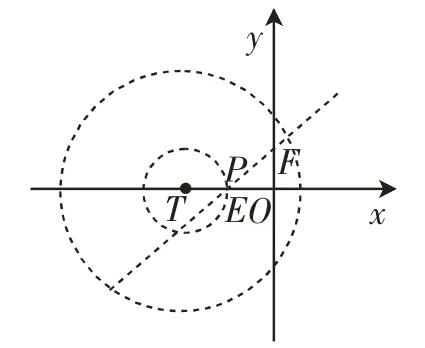
图6

例2在平面直角坐标系xOy中，对于点A和图形M，若图形M上存在两点P、Q，使得AP=3AQ，则称点A是图形M的“3倍点”.

（1）若图形M为线段BC，其中点B（-2，0）和C（2，0），试分析三个点D（-1，2）、E（-1，1）、F（0，2）中，哪个点是线段BC的“3倍点”.

（2）以原点为圆心、4为半径的⊙O，探究直线y=-x+2上⊙O的“3倍点”的横坐标x0的取值范围.

（3）设直线y=-x+1与x轴、y轴分别交于点H、G，⊙T的半径为4，圆心T是x轴上的动点，分析线段GH上是否存在⊙T的“3倍点”.如果存在，画图并分析圆心T的横坐标t的取值范围；如果不存在，请说明理由.

教学记录：（1）画出图形，不难分析出点E符合要求；

（2）主要是分析出两个同心圆（半径分别为2、8）组成的“圆环”内部的点符合要求，进一步构造图形分析，如图7，

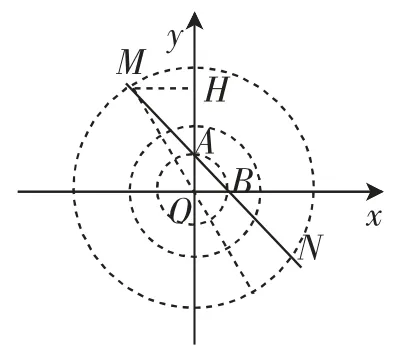
图7

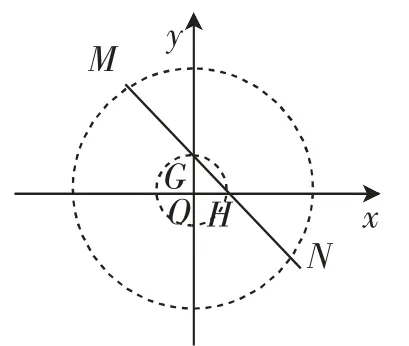
图8

以2为半径的圆与x轴的正半轴、y轴的正半轴恰交于（2，0）、（0，2）两点，正好对应着直线y=-x+2与坐标轴的交点B、A，而以8为半径的大圆与直线y=-x+2交于M、N两点，可见被半径为2、8的图组成的圆环“圈住”的直线y=-x+2的两段线段AM、BN，只要分析出这4个端点的横坐标可得答案，即

（3）理解起来有点难度，在图7的基础上，我们画出直线y=-x+1，观察同心圆O（半径分别为2、8）组成的圆环与线段GH是没有公共点的，现在将这个“圆环”沿x轴方向左右平移，可以得到4处临界状态（如图9～12），从而得到

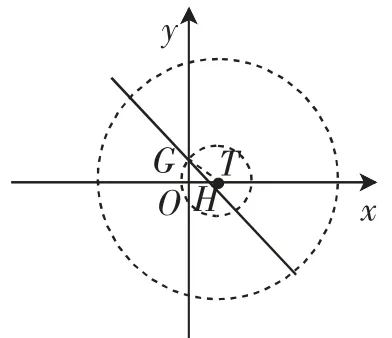
图9

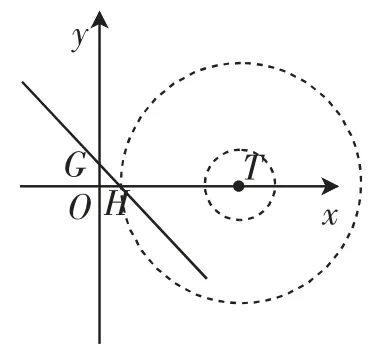
图10

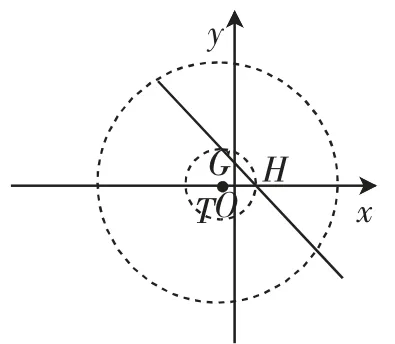
图11

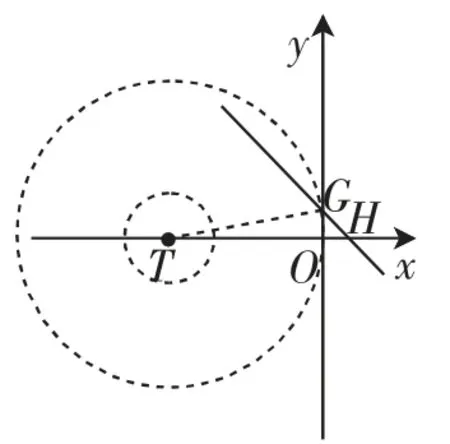
图12

回顾反思：上面两道例题讲评过程中（主要是最后一问），需要先引导学生想清辨明两个同心圆，然后左右平移这组同心圆，观察“圆环”与线段是否存在公共点情况，找出4个临界位置，从而得出圆心所在位置横坐标的取值范围.

二、关于新定义考题的教学思考

1.通过构图将抽象、晦涩的思路生动、形象地揭示出来

像本文关注的这类新定义考题，到了最后一问的思路都非常抽象、晦涩，如果只是满足于简单的讲解思路、列式得出方程、求出解集，则多数学生往往不知所云.这就需要教师在课前对问题的思路要有深刻的理解，对学生理解的关键点、障碍点、易错点要有精准的研判.在此基础上，要努力通过构图（对于动态问题通过分解构图），将抽象、晦涩的思路生动、形象地揭示出来，促进学生更好地理解.在上文例1、例2的最后一问构图时，我们将不同临界情形都进行了构图，帮助学生理解如何确定临界位置，以及在这种位置下如何求解相应的横坐标的取值范围.在构图过程中，教师还需要向学生传递排除干扰的策略，比如，对于一些无关的线条或图形区域，要引导学生对局部图形进行放大或缩小（可以称之为“缩放技术”），以便对问题的思路获得更理想的视觉效果.

2.较难问题讲评要通过同类链接促进学生深刻理解

新定义问题往往都处于一份试卷中的把关题位置，这时如果就题论题、浅层次讲评（核对答案或抄写解题步骤），学生对这些较难题的理解难以走向深处，需要我们在讲评之前精心准备、认真备课.除了上面提及的要将抽象、晦涩的思路尽可能生动、形象地揭示出来，还可通过同类问题的链接讲评或同类跟进再练，来促进学生深刻理解，这也是上文我们在讲评时选用两道同类例题的教学立意.当然，同类问题的选择也是一个教研难点，更多的是靠教师“进入题海”进行大量解题，遴选出相同结构的习题进行同类链接，而不能只是“形似质异”，即形式上相同，而问题的结构或解题的关键步骤都“风马牛不相及”.

三、写在后面

解题研究是不少教师的爱好，然而从解题研究走向解题教学研究却没有得到一些教师的充分重视，从一些教辅资料或公众号文章能看出有些教师在解法研究上用功很多，但有些“一题多解”是否适合直接进入课堂是值得商榷的，一是因为课堂教学时间有限，二是有些解题涉及更多的“高一级结论”，并不适合简单向学生进行推介，让学生记住这些结论，会加重学生学习负担，因为数学解题教学最关键的是要倡导“回到定义”的“更初等的解法”，想来，这也是积极践行“数学，根本上是玩概念，不是玩技巧”（李邦河院士语）.