数据缺失环境下基于DCTPLS-PCA的路网速度预测研究

姚加林，朱闯

数据缺失环境下基于DCTPLS-PCA的路网速度预测研究

姚加林，朱闯

(中南大学 交通运输工程学院，湖南 长沙 410075)

准确可靠的短时交通流预测是实现良好交通控制与诱导的基础，由于设备故障和通信干扰等原因，交通数据经常存在缺失现象，给交通流预测造成了很大困难。在数据缺失环境下，通过基于三维离散余弦变换的补偿最小二乘回归(DCT-PLS)算法对缺失数据进行修复，利用主成分分析(PCA)对修复后的数据降维，用K近邻(KNN)算法预测路网中各路段速度，并计算预测误差。以长沙市某路网为例，在数据完整和数据缺失2种情况下进行数值实验。研究结果表明：DCT-PLS算法修复精度高于概率主成分分析(PPCA)和贝叶斯主成分分析(BPCA)；PCA降维能够大幅减少预测时的计算成本；在数据缺失环境下，基于DCTPLS-PCA的方法在大幅降低计算成本的同时，能够保证很好的预测精度。

数据缺失；DCT-PLS；PCA；路网；速度预测

随着经济社会的快速发展，小汽车保有量急剧增加，由此导致了日益严重的城市交通拥堵问题。智能交通系统被认为是缓解城市交通拥堵的重要方案之一，交通控制与诱导是城市交通管理中的重要组成部分，在智能交通系统中发挥着举足轻重的作用。而准确可靠的短时交通流预测是实现良好交通控制与诱导的基础，因此研究短时交通流预测对于缓解城市拥堵具有重要意义。数据采集是实现交通流预测的第一步，然而在交通数据采集过程中，由于设备故障、通信干扰等原因，经常存在数据缺失现象，这给准确的交通流预测造成巨大困难。在加拿大亚伯达7 a的交通数据中有近50%的数据存在缺失，某些时段缺失比例更是高达90%[1]。数据修复是处理缺失数据的常用方法，数据修复算法可分为3类，第1类为基于向量的修复方法，包括近邻方法[2]，回归补值方法[3−4]等。第2类为基于矩阵的修复方法，包括概率主成分分析(PPCA)和贝叶斯主成分分析(BPCA)[5−6]等。第3类为基于张量的修复方法，包括CP分解方法和Tucker分解方法[7]等。基于矩阵的修复方法具有修复精度高、速度快的优点，在交通数据修复领域应用广泛，PPCA和BPCA是其中常用的2种算法。但是当缺失率高时，上述2种算法的修复结果不尽如人意。基于三维离散余弦变换的补偿最小二乘回归(penalized least square regression based on three-dimensional discrete cosine transform，DCT-PLS)算法在高缺失率时仍能保证很高的修复精度[8−9]，本文首次将该算法引入交通数据修复领域。以往的研究[10−12]多是预测单个路段上车辆的速度，但是单个路段的交通信息对于交通管理与控制的指导作用有限，因此，本文以路网为研究对象，预测路网内各路段的速度，为交通管控提供更全面的信息。当研究对象由路段扩展为路网，带来了数据量激增的问题，特别是对于数据驱动的预测方法而言，数据量的激增会导致难以承受的计算成本。为解决该问题，引入数据降维技术以降低计算成本。主成分分析(Principal Component Analysis，PCA)计算简单，易于实现，是常用的降维方法，本文采用该方法对修复后的数据降维。综上，在数据缺失环境下，本文首先采用DCT-PLS算法对缺失数据进行修复，然后应用PCA算法对修复后的数据降维，最后以该数据作为实验数据，用K近邻(K nearest neighbors，KNN)算法预测路网内各路段速度。

1 研究方法

1.1 DCT-PLS算法

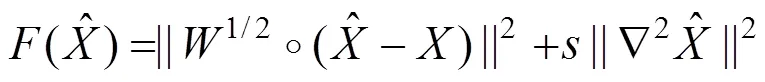
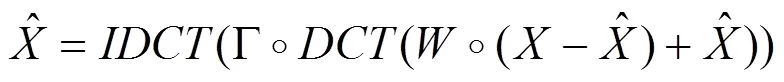
其中：i表示第维的第个元素，n表示的第维的大小。

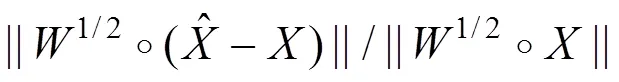
根据归一化误差，即可由DCT-PLS预测缺 失值。

1.2 PCA算法

PCA是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。其步骤为：

1) 数据标准化：设有个向量，个样本点的矩阵，将矩阵标准化，得到矩阵矩阵的相关系数矩阵设为。

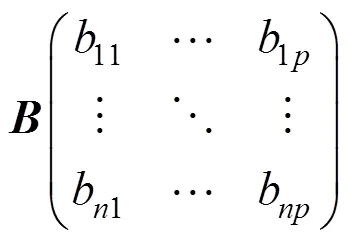
其中：

2) 计算矩阵的特征值与特征向量：解特征方程求得特征值λ(=1, 2, …,)然后求出特征值对应的正交化单位特征向量e(=1, 2, …,)

3) 计算主成分贡献率及累计贡献率

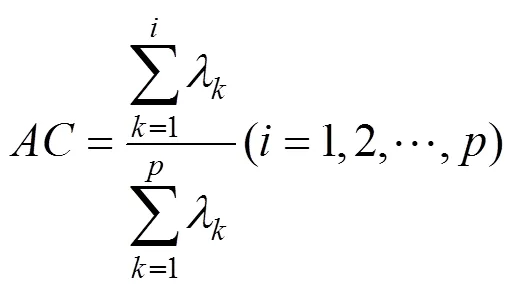
4) 计算主成分载荷

5) 计算各主成分得分

其中：为选取的主成分个数，其值取决于使用者选定的累计贡献率阈值。

1.3 KNN算法

K近邻(KNN)算法是一种典型基于数据驱动的算法，具有参数少，易于拓展的优点。其算法步骤如下：

1) 将数据分成2部分，一部分作为训练数据，另一部分作为测试数据。

2) 选定参数

3)维护一个大小为，按距离由小到大排列的最近邻数组；维护一个大小为K的优先级队列。

4) 遍历训练数据，计算当前训练数组与测试数组的距离，将该距离与最近邻数组中最大距离max比较。

5) 若>=max，则舍弃该数组，遍历下一个数组。若＜max，删除优先级队列中最大距离的数组，将当前训练数组存入优先级队列。

6) 遍历完毕，计算优先级队列中个数组的多数类，并将其作为测试数组的类别。

2 实验场景与数据处理

2.1 实验场景

选取长沙市中心城区某一路网为研究对象，该路网内包含4个信控交叉口和26个路段。路段上的出租车GPS数据被用来估算该路段上车辆的平均速度。GPS数据包含以下信息：路段编号、每个路段上出租车数量、出租车运行速度、时间戳等。该数据的采样间隔为2 min，因此每天采集720个数据。本文使用16 d共11 520个数据作为实验 数据。

实验路网图如图1所示，其中图1(a)为卫星图；图1(b)为路网拓扑结构图，为方便表示和阅读，将路段重新进行了编号。

图1(a)中未被编号的建湘路将蔡锷路和芙蓉路之间的人民路分为2个路段(即路段1070201/ 1070301，相反方向为1070303/1020703)，在此情况下，本文将同方向2个路段视为一个路段(路段11，相反方向编号12)，其速度值取2个路段上车辆速度的平均值。因此，实验路网中总包含24个路段。

2.2 数据缺失形式

在数据采集过程中，由于设备故障、通信干扰等原因，采集到的数据经常存在缺失的情况。根据缺失的形式不同，可以分为3种形式即随机缺失、模块缺失和混合缺失。本文中，在随机缺失情况下，产生一系列随机位置，该位置的数据缺失，用NaN代替。在模块缺失情况下，产生一系列随机位置，该位置及之后的个数据连续缺失(本文取10)，用NaN代替。值得注意的是，该随机数序列中，各随机数之间的差值不得小于-1。当数据混合缺失时，首先将数据平均分为2部分，一部分数据采用随机缺失的方法处理，另一部分采用模块缺失的方法处理。将数据分组可以避免出现同一个数据多次缺失的情况。

(a) 卫星图；(b) 拓扑结构图

另外，为了衡量修复误差及预测误差，采用3个常用指标，即平均绝对误差(Mean Absolute Error，MAE)、平均绝对百分比误差(Mean Absolute Percent Error，MAPE)、均方根误差(Root Mean Square Error，RMSE)。

3 数值实验

3.1 修复算法比较

PPCA和BPCA是修复交通数据常用的算法，本文从修复精度和计算时间2个维度比较PPCA、BPCA与DCT-PLS。

实验数据缺失率从10%开始，以10%的步长递增至90%。因为数据缺失位置(或缺失起始位置)是随机产生的，为了降低随机因素对实验结果的影响，每种缺失率下均进行10次重复实验。

表1~3列出了10次实验的平均MAPE(10次实验结果方差很小，这里没有列出)。值得注意的是，表中列出的时间为90次实验的总时间。另外，在缺失率较高时，BPCA算法在短时间内(10 min)无法完成修复工作，因此，表中没有列出其相应的修复误差及总计算时间。

从表1可知，随机缺失时，在各缺失率下，DCT-PLS的修复精度均最高。当缺失率超过70%时，DCT-PLS的修复精度比PPCA高出10%。PPCA的修复精度较DCT-PLS略低，但是其运行速度更快。BPCA在缺失率不超过50%时，修复精度与PPCA及DCT-PLS相当，但是随着缺失率进一步增加，该算法难以在短时间内完成修复工作。

图2 3种缺失形式示意图

表1 随机缺失下不同算法修复误差

表2 模块缺失下不同算法修复误差

表3 混合缺失下不同算法修复误差

模块缺失时，由表2可知，当缺失率不超过50%时，PPCA修复精度最高，随着缺失率继续增加，PPCA的修复误差增长较快。

DCT-PLS在高缺失率时优势明显，当缺失率达到80%时，其误差低于20%，且较PPCA低10%左右。BPCA在低缺失率时修复精度与PPCA及DCT- PLS相近，但是当缺失率较高时，该算法的计算成本迅速增加。

与模块缺失类似，混合缺失时，由表3可得，缺失率较低时，PPCA修复较高，随着缺失率增加，其修复误差快速增加。随着缺失率增加，DCT-PLS的修复误差也逐渐增加，但是其误差增长幅度小于PPCA,特别是缺失率高于60%后，其误差增长明显低于PPCA。BPCA同样在低缺失率时修复精度较好，但是无法在短时间内完成高缺失率数据的 修复。

综上所述，相较于PPCA、DCT-PLS，BPCA算法在修复精度和运算时间上均没有优势。PPCA算法计算速度快，在低缺失率时，修复精度高，当缺失率不超过50%时，建议采用PPCA算法进行数据修复。DCT-PLS算法计算速度较PPCA略慢，但是在各种缺失率下，其修复精度均较高，特别是高缺失率时(缺失率>60%)，其修复精度明显高于另外2种算法，因此在高缺失率时，建议采用DCT-PLS算法。后续的预测实验中数据缺失率很高，因此采用DCT-PLS作为本文的修复算法。

3.2 预测实验

3.2.1 实验参数设定

本文将前15 d的数据作为KNN算法的训练数据，第16 d数据作为测试数据，同时，根据经验将K近邻算法中K值设为5。因为GPS数据周期为2 min，因此本文的预测周期设为2 min。另外，模块缺失中参数设为10，主成分分析中累计概率阈值取值设为90%。

3.2.2 数据完整情况

在数据完整情况下，不需要使用DCT-PLS修复数据，直接用PCA算法对数据降维。数据降维后，使用KNN算法预测。

一次预测能够输出全部24个路段的预测值及相应误差，但是由于版面限制，无法对各个路段进行单独分析，因此取24个路段的平均误差作为路网的预测误差，结果见表4。

由表4可知，在数据完整情况下，KNN能较好的预测路网上各路段的速度值。

表4 数据完整情况下路网预测误差

3.2.3 数据缺失情况

在数据缺失情况下，首先使用DCT-PLS算法对缺失数据进行修复，之后用PCA方法降维，最后使用KNN算法预测。同样的，为了避免随机因素对结果的影响，每组实验重复10次。

表5列出来了数据降维的结果(10次实验平均值)。同样的，由于版面限制，无法对路网内各路段的预测结果进行单独分析，只列出路网内所有路段的平均预测误差。表6~8中列出了10次实验的平均误差，图3以盒图的形式展示了10次实验的 结果。

另外，城市交通网络具有很强的时效性，为了验证本文提出的方法的广泛适用性，在3种缺失形式下，分别计算了全天平均预测误差(即表6)，8:00~9:00时段的误差(表9)及20:00~21:00时段的预测误差(表10)。

表5 PCA降维后列向量个数

表6 随机缺失下路网平均误差

表7 模块缺失下路网平均误差

表8 混合缺失下路网平均误差

表9 随机缺失下路网平均误差(8:00~9:00)

表10 随机缺失下路网平均误差(20:00~21:00)

图3 10次实验预测误差(MAPE)

由表5可知，应用PCA之后数据变为2-12列，降维之后的数据量约为原始数据的1/12-1/2(降维之前数据由24个列向量组成(24个路段))。比较不同缺失率的降维效果可知，缺失率越高降维后剩余的数据量越少。当缺失率为90%时，降维后的数据量仅为原始数据的1/12，与原始数据中不缺失数据量(10%)相当。另外，本文中应用PCA完成一次降维所需时间约为0.5 s，相对于预测时间可以忽略不计，因此使用数据降维技术可以大幅降低基于数据驱动的预测方法的计算成本。

从表6可知，随着数据缺失率的增加，平均误差也相应增加。当缺失率为10%时，预测误差为16.18%，与不缺失时的误差相近；当缺失率为50%时，预测误差为18.82，比不缺失时增加2.80%；当缺失率达到90%时，MAPE也仅为26.53%，较数据完整时增加了10%，MAE为4.6511，较不缺失时增加约0.8。

在模块缺失时，由表7可得，预测误差同样随着缺失率增加而逐渐增加。缺失率为10%时，误差为17.15%，较数据完整时增加1.13%；缺失率达到90%时，MAPE为24.33%，较不缺失时仅增加8%，而MAE为4.508 0，比不缺失时增加约0.7。

由表8可知，混合缺失时，当缺失率在50%以下时，预测误差均小于20%，较不缺失情况仅仅增加4%。当缺失率继续增加时，预测误差随之增加，但是增加幅度较小。缺失率为90%时，误差也仅为24.87%，较不缺失时仅仅增加了8%，MAE为4.529 0，比不缺失时增加约0.7。

在随机缺失环境下，由表6、表9可知，8:00~ 9:00时段的预测误差低于全天平均误差。对比表6和表10可知，20:00~21:00时段的MAE及RMSE值低于全天的对应值，但是其MAPE值比全天平均MAPE值高。全天平均、8:00~9:00时段及20:00~ 21:00时段的预测误差存在差异但预测精度均较好。在模块缺失及混合缺失环境下可得出与随机缺失环境下相同的结论。

从图3中可以看出,随着缺失率增加，MAPE值随之增加(对MAE、RMSE有相同结论)。比较不同缺失形式可知，随机缺失时预测效果最好，混合缺失次之，模块缺失最差。另外，从盒图可以看出不同缺失率下，随机缺失时10次实验结果的方差最小，模块缺失与混合缺失方差相近。

4 结论

1) PPCA算法效率最高，DCT-PLS算法效率略低，BPCA算法的效率明显低于上述2种算法。在低缺失率时，3种算法的修复精度相近；在高缺失率时，DCT-PLS算法优势明显，其修复精度比PPCA高10%左右。

2) 使用PCA算法降维后数据量变为原来的1/2-1/12，说明使用降维技术可以大幅减少数据量，从而降低预测时的计算成本。

3) 3种缺失形式下，当缺失率为10%时，预测误差较数据完整时仅增加1%左右，当缺失率达到90%时，预测误差也仅增加10%左右，证明在数据缺失环境下，基于DCTPLS-PCA的方法在大幅降低计算成本的同时，能够保证很好的预测精度。

[1] 徐健锐, 李星毅, 施化吉. 处理缺失数据的短时交通流预测模型[J]. 计算机应用, 2010, 30(4): 1117−1120. XU Jianrui, LI Xingyi, SHI Huaji. Short-term traffic flow prediction model for processing missing data[J]. Computer Applications, 2010, 30(4): 1117−1120.

[2] Smith B, Scherer W, Conklin J. Exploring imputation techniques for missing data in transportation management systems[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003(1836): 132− 142.

[3] CHEN C, Kwon J, Rice J, et al. Detecting errors and imputing missing data for single-loop surveillance systems[J]. Transportation Research Record: Journal of the Transportation Research Board, 2003 (1855): 160− 167.

[4] ZHONG M, Lingras P, Sharma S. Estimation of missing traffic counts using factor, genetic, neural, and regression techniques[J]. Transportation Research Part C: Emerging Technologies, 2004, 12(2): 139−166.

[5] QU L, LI L, ZHANG Y, et al. PPCA-based missing data imputation for traffic flow volume: A systematical approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(3): 512−522.

[6] LI L, LI Y, LI Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence[J]. Transportation Research Part C: Emerging Technologies, 2013(34): 108−120.

[7] Kolda T G, Bader B W. Tensor decompositions and applications[J]. SIAM Review, 2009, 51(3): 455−500.

[8] Garcia D. Robust smoothing of gridded data in one and higher dimensions with missing values[J]. Computational Statistics & Data Analysis, 2010, 54(4): 1167−1178.

[9] WANG G, Garcia D, LIU Y, et al. A three-dimensional gap filling method for large geophysical datasets: Application to global satellite soil moisture observations [J]. Environmental Modelling & Software, 2012(30): 139−142.

[10] ZHENG L, ZHU C, ZHU N, et al. Feature selection- based approach for urban short-term travel speed prediction[J]. IET Intelligent Transport Systems, 2018, 12(6): 474−484.

[11] TANG J, LIU F, ZOU Y, et al. An improved fuzzy neural network for traffic speed prediction considering periodic characteristic[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(9): 2340−2350.

[12] MA X, DAI Z, HE Z, et al. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction[J]. Sensors, 2017, 17(4): 818.

Research on road network speed prediction based on DCTPLS-PCA under data missing

YAO Jialin, ZHU Chuang

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Accurate and reliable short-term traffic flow prediction is the basis of traffic control and guidance. However, traffic data missing that result from communication interference and other reasons, makes traffic flow prediction difficult. In this paper, the compensated least square regression algorithm (DCT-PLS) based on 3D discrete cosine transform was used to repair the missing data, and then the dimension of the repaired data was reduced by principal component analysis (PCA). Finally, the K-nearest neighbor (KNN) algorithm was used to predict the speed of each link of the road network, and the prediction error is calculated. The numerical experiments were conducted with and without the data missing based on a real network information in Changsha. The results show that the accuracy of repairing data of DCT-PLS algorithm is higher than that of probabilistic principal component analysis (PPCA) and Bayesian principal component analysis (BPCA); PCA can greatly reduce the computational cost of prediction. Under data missing, the method based on DCTPLS-PCA can greatly reduce the computational cost and ensure good prediction accuracy.

data missing; DCT-PLS; PCA; road network; speed prediction

U491

A

1672 − 7029(2019)10− 2612 − 08

10.19713/j.cnki.43−1423/u.2019.10.030

2019−01−01

姚加林(1961−)，男，湖南娄底人，副教授，从事交通运输规划与管理研究；E−mail：yaojialn@csu.edu.cn

(编辑 蒋学东)