基于票额分配的高速铁路动态定价分治优化方法
邓连波,曾宁鑫,陈雨欣,肖龙文
基于票额分配的高速铁路动态定价分治优化方法
邓连波,曾宁鑫,陈雨欣,肖龙文
(中南大学 交通运输工程学院,湖南 长沙 410075)
研究基于票额分配的高速铁路多列车多OD的动态定价问题。以多列车的总收益最大为目标函数,建立多列车多OD的动态定价和票额分配联合优化模型,并在约束条件中充分考虑实际运营的需要。设计了将模型分解为双层规划的分治优化方法,通过票额分配与动态票价的分治优化,有效降低该类大规模问题的求解难度,并提高了求解效率。最后用20列车350个乘车OD的大型算例对模型和方法进行验证,为高速铁路动态定价的实际应用提供支持与参考。
高速铁路;动态定价;票额分配;多列车;分治优化

随着中国高铁网络的迅速发展,中国已经从政策层面逐步放开了高铁的自主定价权,并在部分线路上进行了尝试。在政策实施的大背景下,借鉴其他行业应用收益管理的成功经验,将收益管理理论与方法应用到我国高速铁路票价制定体系中,对提升高速铁路的运营效率和收益具有重要的现实意义。收益管理的主要内容包括需求预测、超售、座位分配和动态定价4个部分。对于铁路行业而言,动态定价和座位分配是最适用的策略和手段。国内外学者对动态定价和座位分配问题大部分针对2个问题单独研究。Weatherford[1]首先考虑了定价和座位分配联合优化问题,研究对象是民航的单航班。此后FENG等[2−3]也研究了单航班的定价和座位分配联合优化问题。Chew等[4]研究了单一产品动态定价和座位分配联合优化的一般问题。而Kuyumcu等[5−9]研究了多航班的动态定价和座位分配联合优化的问题。在铁路研究领域,Ongprasert[10]研究了与民航竞争环境下日本城际高速铁路的座位分配问题,提出了考虑乘客选择和折扣票价的多列车多OD座位分配模型。Hetrakul等[11]利用数学规划模型研究了城际铁路多列车多OD的定价和座位分配问题。杨宇航等[12]基于旅客对票价变化的敏感程度研究了高速铁路多列车差别定价策略。郑金子[13]研究了多列车多阶段的动态定价问题,在每一阶段进行差异化定价,对整个模型采用近似动态规划方法求解。宋文波等[14]研究了单列车多OD动态定价与票额分配综合优化问题,运用稳健优化方法对模型进行求解。赵翔等[15]利用票价和票额综合优化,研究了高速铁路多列车差别定价方法。上述大部分文献提出的方法仍然不具有普适性或只适用于小规模问题,并且在考虑座位分配时大都是从乘客的角度出发,基于乘客的效用或选择来“被动”进行座位分配。本文在座位分配和动态定价时均以收益最大化为目标,建立多列车多乘车OD的动态定价和座位分配联合优化模型,采用分治优化的方法来降低求解难度。
1 问题描述
1.1 基本假设
1) 假设只考虑单一线路一个方向的情况,多列车、多停站。在同一OD对起终点车站设置了停站的列车集可以互相视作可替代品,各趟列车具有不同起讫点和停站方案。
2) 假定各OD对之间的出行需求是相互独立的。各个OD选择某一列车的客流共同构成列车相邻停站区间的断面流,需要满足列车能力约束。
3) 不同旅客愿意支付不同的价格购买相同的座位。每趟列车的定价、速度(旅行时间)和乘降时刻等会影响乘客出行行为。同时忽略因票价波动发生的退票情况。
4) 假定需求函数已知,不同OD的需求弹性在同一时间相同。将预售期划分为若干售票时段,根据每个售票时段开始时各OD的剩余席位数,确定该时段计划发售车票的票价和数量。
1.2 符号定义
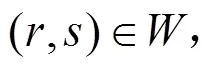
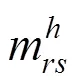

采用广义费用的指数函数来刻画客流需求。给定O-D对(,),具有相同O-D对(,)的全部高铁旅客运输产品的分时段弹性需求函数可以描述为以下形式


所以,服务于O-D对(,)所有列车的每个旅客平均费用


2 模型构建
以所有列车所有乘车OD各个售票时段的总售票收益最大化为优化目标,目标函数为

约束条件包含了列车能力约束,非负约束和各类票价约束。
1) 每一趟列车各区间的能力约束。

2) 售票数量非负约束。
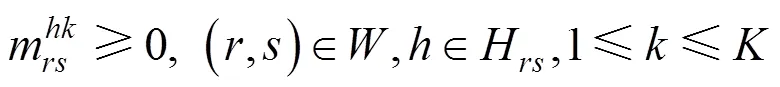
3) 售票数量不大于需求量。
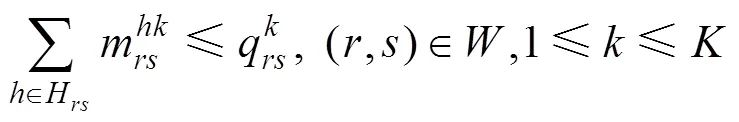
4) 票价上下界约束:任何时段、任何列车、任何点对的票价均满足上下限的约束。

5) 同一列车长程票价不低于短程票价。
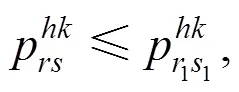

6) 同一列车、同一点对的票价随着发车时间的接近而单调增加(或者不下降)。

上述模型可以等价转换成一个双层规划模型,其中上层主规划模型是多列车多乘车OD的票额分配模型,下层子规划模型是单列车单乘车OD的动态定价模型,将多列车的动态价格策略问题分解为多列车的票额分配计划和各列车各乘车OD的动态定价策略2部分。
2.1 上层主规划模型:票额分配模型(M1)
以所有列车所有乘车OD各个售票时段的总售票收益最大化为优化目标,目标函数为:

约束条件仅包含预售期内各列车的能力约束。

2.2 下层子规划模型:单列车单乘车OD的动态定价模型(M2)
以单列车单乘车OD各个售票时段的总售票收益最大化为优化目标,目标函数为:


将式(15)变换可得

约束条件包含乘车OD的票额约束、售票数量非负约束和各类票价约束。
该乘车OD的票额约束为

其他约束条件与式(7),(9),(10)和(11)一致。
3 模型求解



再结合式(1),可得

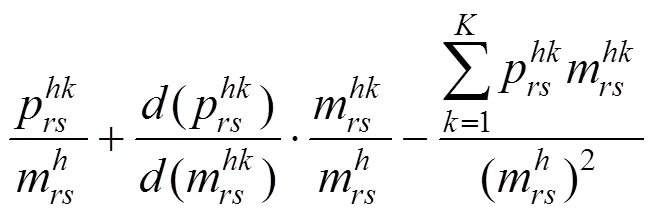

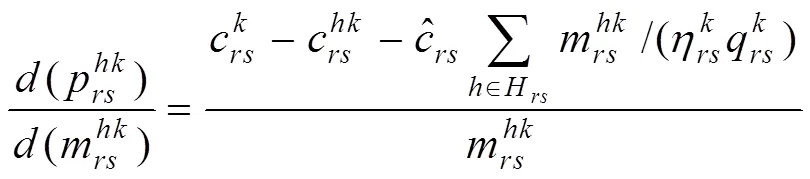
将式(21)代入式(20),可得:
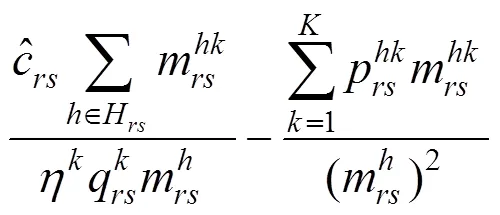
约束条件包含能力约束和售票数量非负约束。能力约束与式(13)一致,非负约束如下:

5) 返回2)。
该方法通过模型分解有效降低了求解难度。模型中,M1’求解宏观票额分配这一静态问题,约束条件是线性的,是高维二次规划问题,M2求解票额分配下单列车单乘车OD的动态票价,是维数较低的非线性规划问题,同时可以在前次求解方案的邻域内迭代,提高了求解效率。

图1 模型求解流程图
4 算例分析
选取2014年7月1日武汉站到深圳北站这一段线路下行方向的20趟列车作为优化对象。20趟列车包含了该段线路上各种起讫点,具体如表1 所示。

表1 算例列车组成表


图2 总收益收敛图

图3 总客座公里收敛图

表2 G6215次列车的优化前后结果对比
为了更直观地呈现优化后的结果,选取从广州南到深圳北的G6215次列车,以表格的形式对优化前后的结果进行对比。从表2可以看出,优化后各OD各阶段的票价均满足模型中各项约束条件,是可行的。同时典型列车的在收益和客座公里在8次以后也都趋于收敛。
5 结论
1) 构建以多列车总收益最大化为目标函数的数学规划模型,并从实际运营的角度考虑,将列车能力限制、票价的各种约束纳入了约束条件,使模型更贴近现实需求。
2) 在求解时针对问题规模较大的情况,提出分治策略的求解方法,通过将模型分解为双层规划模型的等价变换,利用票额分配与动态票价的分治求解,有效降低了求解难度,并有效利用解的邻域进行搜索,提高了求解效率。
3) 以实际运营情况作为基础数据进行了20列车总计350个乘车OD的大规模算例分析。优化后收益增长了2.19%,且快速收敛,得到了各方面均符合预期的结果,验证了模型的正确性和求解方法的有效性。
[1] Weatherford L. Using prices more realistically as decision variables in perishable-asset revenue management problems[J]. Journal of Combinatorial Optimization, 1997, 1(3): 277−304.
[2] FENG Y, XIAO B. Integration of pricing and capacity allocation for perishable products[J]. European Journal of Operational Research, 2006, 168(1): 17−34.
[3] Cizaire C. Optimization models for joint airline pricing and seat inventory control: Multiple products, multiple periods[D]. America: Massachusetts Institute of Technology, 2011.
[4] Chew E P, Lee C, Liu R J. Joint inventory allocation and pricing decisions for perishable products[J]. International Journal of Production Economics, 2009, 120: 139−150.
[5] Kuyumcu A, Garcia D A. A polyhedral graph theory approach to revenue management in the airline industry[J]. Computers and Industrial Engineering, 2000, 38(3): 375−395.
[6] Bertsimas D, de Boer S. Joint network pricing and resource allocation[EB/OL].
[7] Cote J, Marcotte P, Savard G. A bilevel modeling approach to pricing and fare optimization in the airline industry[J]. Journal of Revenue and Pricing Management, 2003, 2(1): 23.
[8] Walczak D, Brumelle S. Semi-Markov information model for revenue management and dynamic pricing[J]. OR Spectrum, 2007, 29(1): 61−83.
[9] 曹海娜. 基于MNL模型的平行航班舱位控制与动态定价研究[D]. 北京: 北京理工大学, 2015. CAO Haina. Research on seat allocation and dynamic pricing for parallel flights with multinomial logit model[D]. Beijing: Beijing Institute of Technology, 2015.
[10] Ongprasert S. Passenger behavior on revenue management systems of inter-city transportation[D]. Japan: Kochi University of Technology, 2006.
[11] Hetrakul, Pratt, Cinzia Cirillo. A latent class choice based model system for railway optimal pricing and seat allocation[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 61: 68−83.
[12] 杨宇航, 张琦. 京沪高速铁路票价调整与优化策略研究[J]. 铁道科学与工程学报, 2017, 14(10): 2043−2049. YANG Yuhang, ZHANG Qi. Research on ticket price adjustment and optimization strategy of Beijing-Shanghai high speed railway[J]. Journal of Railway Science and Engineering, 2017, 14(10): 2043−2049.
[13] 郑金子. 高速铁路票价动态优化方法的研究[D]. 北京: 北京交通大学, 2017. ZHENG Jinzi. Research on ticket fare dynamic optimization for high-speed train[D]. Beijing: Beijing Jiaotong University, 2017.
[14] 宋文波, 赵鹏, 李博. 高速铁路单列车动态定价与票额分配综合优化研究[J]. 铁道学报, 2018, 40(7): 10−16. SONG Wenbo, ZHAO Peng, LI Bo. Research on comprehensive optimization of dynamic pricing and seat allocation for high-speed single trains[J]. Journal of the China Railway Society, 2018, 40(7): 10−16.
[15] 赵翔, 赵鹏, 姚向明, 等. 高速列车折扣票价与票额分配组合优化模型[J]. 东南大学学报(自然科学版), 2018, 48(4): 759−765. ZHAO Xiang, ZHAO Peng, YAO Xiangming, et al. An integrated optimization model of discount fare and ticket allocation for high-speed train[J]. Journal of Southeast University (Natural Science Edition), 2018, 48(4): 759− 765.
A divide-and-conquer optimization method for dynamic pricing of high-speed railway based on seat allocation
DENG Lianbo, ZENG Ningxin, CHEN Yuxin, XIAO Longwen
(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)
This paper studies the dynamic pricing problem based on seat allocation of multiple trains and multiple O-D itineraries on high speed railway. Take the maximum total revenue of multiple trains as the objective function. A joint optimization model of dynamic pricing and seat allocation for multiple trains and multiple O-D itineraries was established. The actual operation requirements were fully considered in the constraint conditions. The model was decomposed into a bilevel programming to solve the problem. Dynamic price and seat allocation were optimized by divide-and-conquer method. The difficulty of solving this kind of large-scale problem was reduced effectively. And improve the solving efficiency. Finally, the model and method were verified with a large scale of example with 20 trains and 350 O-D itineraries. It provided support and reference for the practical application of dynamic pricing.
high speed railway; dynamic pricing; seat allocation; multiple trains; divide-and-conquer optimization
U293
A
1672 − 7029(2019)10− 2407 − 07
10.19713/j.cnki.43−1423/u.2019.10.004
2019−01−15
国家自然科学基金资助项目(71471179);中国铁路总公司重点课题(N2018X009)
邓连波(1977−),男,辽宁昌图人,教授,从事交通运输规划与管理研究;E−mail:lbdeng@csu.edu.cn
(编辑 阳丽霞)

