板端离缝下CRTSⅢ型板式轨道动力特性研究

刘平，武欣，徐浩

板端离缝下CRTSⅢ型板式轨道动力特性研究

刘平1，武欣1，徐浩2

(1. 河北轨道运输职业技术学院 车辆系，河北 石家庄 050000；2. 中铁二院工程集团有限责任公司，四川 成都 610031)

轨道板与自密实混凝土层之间的板端离缝是CRTSⅢ型板式轨道的主要伤损型式之一，为分析板端离缝对路基上CRTSⅢ型板式轨道动力特性的影响，建立车辆-CRTSⅢ型板式轨道−路基垂向耦合振动模型，研究不同板端离缝长度对车辆和轨道系统动力响应的影响。研究结果表明：板端离缝将增大车辆和轨道结构的动力响应。当脱空长度超过1.54 m时，轨道结构的垂向位移出现拐点，扣件系统上拔力接近允许限值10 kN，板端离缝区域附近的自密实混凝土层所受的垂向压应力增大28.75倍。板端离缝导致自密实混凝土层更易发生劣化，从无砟轨道耐久性方面考虑，建议当CRTSⅢ型板式轨道板端离缝长度达到1.54 m时应及时进行养护维修。

CRTSⅢ型板式轨道；板端离缝；高速列车；动力响应；养护维修

CRTSⅢ型板式无砟轨道是结合成都至都江堰铁路建设形成的具有自主知识产权的无砟轨道结构，目前已在成灌、盘营等线路上应用。然而在运营过程中发现，轨道板与自密实混凝土层之间存在离缝现象。一旦轨道板与自密实混凝土层的离缝严重时，将影响无砟轨道的耐久性和高速列车运行的平稳性与安全性，因此，有必要研究层间离缝对车辆和轨道动力特性的影响。目前，关于层间离缝对车辆−轨道动力特性的影响研究主要针对CRTSⅠ型和CRTSⅡ型板式无砟轨道[1−6]。向俊等[1]认为，CA砂浆层劣化将引起轨道加速度和位移急剧增大，应严格控制CA砂浆病害。LIU等[2]通过建立车辆−无砟轨道−路基耦合动力学模型，研究不同列车速度下由于CA砂浆造成的层间离缝对单元板式轨道动力特性的影响规律，认为当列车速度超过300 km/h，层间离缝长度小于2 m时，几乎不影响行车安全性，但会造成轨道板振动急剧增加。REN等[3]建立考虑底座板脱空的列车−板式无砟轨道动力学模型，研究底座板脱空对日本板式无砟轨道动力特性的影响，认为在短波不平顺下，底座板脱空面积应小于10 m2，长波不平顺性底座板脱空面积应小于14 m2。WANG等[4]通过建立路基上CRTSⅡ型板式无砟轨道动力学模型，研究砂浆脱空对CRTSⅡ型板式无砟轨道动力特性的影响，认为砂浆脱空长度应小于1.95 m。李培刚等[5]建立考虑CA砂浆脱空的桥上板式无砟轨道模型，研究CA砂浆脱空对桥上单元板式无砟轨道动力特性的影响规律，建议砂浆脱空长度不宜超过0.8 m。杨荣山等[6]通过建立考虑CA砂浆伤损的列车−轨道耦合动力学模型，研究砂浆伤损对CRTSⅠ型板式无砟轨道动力特性的影响，认为砂浆伤损沿轨道板纵向宽度不宜超过0.6 m，沿轨道横向宽度不宜超过0.2 m。尽管国内外学者针对层间离缝下CRTSⅠ型和CRTSⅡ型板式无砟轨道动力特性的影响规律开展了大量研究，但是，针对CRTSⅢ型板式无砟轨道动力特性尤其是板端离缝对CRTSⅢ型板式无砟轨道动力特性的研究尚未见报道。周毅等[7−8]分别对路基及桥梁上CRTSⅢ型板式无砟轨道的动力特性进行研究，然而未考虑层间离缝的影响。杨政[9]从静力学的角度研究层间离缝对CRTSⅢ型板式无砟轨道受力特性的影响规律。考虑CRTSⅢ型板式无砟轨道在服役过程中主要承受列车动荷载作用，且轨道板与自密实混凝土层离缝是其主要伤损之一，因此，本文拟通过研究板端离缝对CRTSⅢ型板式无砟轨道系统动力特性的影响规律，从而为无砟轨道的养护维修提供理论支撑。

1 计算模型与求解方法

根据轮轨系统动力学理论[10−12]，建立的列车-CRTSⅢ型板式无砟轨道−路基垂向耦合动力学模型如图1所示。

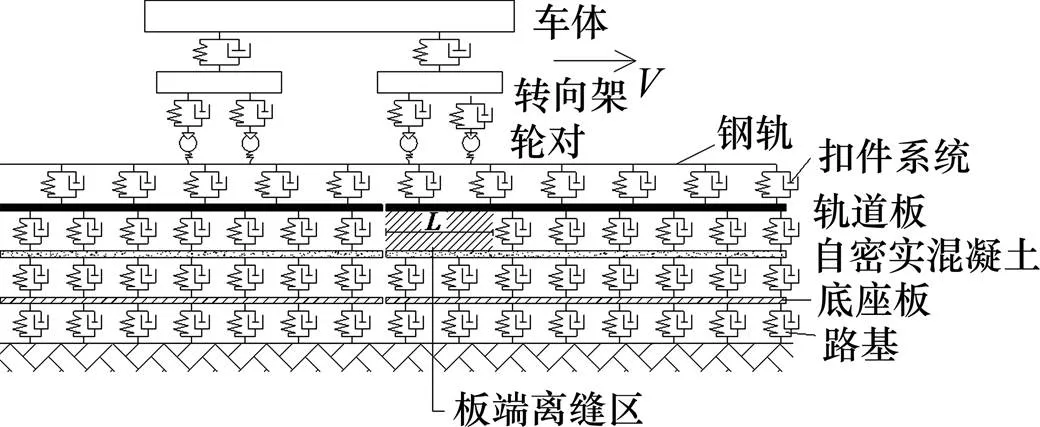
图1 列车-轨道-路基垂向耦合动力学模型

该模型包含列车子系统和轨道子系统2部分，其中列车子系统考虑为多刚体子系统，由车体、转向架和轮对组成。转向架与轮对由一系悬挂连接，车体与转向架由二系悬挂连接，采用弹簧−阻尼单元模拟一系和二系悬挂。模型中车体和转向架考虑沉浮和点头，轮对只考虑沉浮。

轨道子系统采用点支承梁模型，其中钢轨、轨道板、自密实混凝土层和底座板均采用离散弹性点支承Euler梁模拟，采用弹簧阻尼单元模拟扣件系统、路基以及轨道板与自密实混凝土层、自密实混凝土与底座板的层间连接，模型的总长度为150 m。

本文采用大型通用有限元软件ANSYS/LS- DYNA建立高速列车-CRTSⅢ型板式无砟轨道−路基系统垂向耦合动力学模型，如图2所示。模型求解时，采用大型通用显式动力分析程序LS-DYNA内置的求解器进行求解。

图2 车辆-轨道-路基垂向耦合有限元模型

2 计算参数及模型验证

2.1 计算参数

车辆子系统各部分的参数按CRH2型动车组进行取值[7−8]，轨道子系统中，钢轨采用60 kg/m钢轨，弹性模量为2.06×105MPa，扣件系统的垂向刚度为50 kN/m，阻尼为7.5×104N·s/m，扣件间距取为0.63 m，轨道板的尺寸为5.6 m×2.5 m×0.2 m，采用C60混凝土，自密实混凝土的厚度为0.09 m，采用C40混凝土，底座板也采用C40混凝土，尺寸为 16.94 m×3.1 m×0.3 m，路基面刚度取76 MPa/m。轨道不平顺采用德国低干扰谱时域随机不平顺样本，如图3所示。

图3 德国低干扰谱时域随机不平顺样本

2.2 车辆−轨道系统动力响应评价指标

采用动态轮重减载率和车体垂向加速度评价车辆系统的动力响应，取动态轮重减载率限值为0.9，车体垂向振动加速度的舒适度标准为0.13[12](为重力加速度)。

采用轮轨垂向力和轨道动态几何不平顺评价轨道系统的动力响应[7]。轮轨垂向力取值标准：轮轨垂向力峰值max≤170 kN时，为非冲击荷载；轮轨垂向力峰值max≤300 kN 时，为钢轨接头等冲击作用。根据国内外高速铁路的工程实践经验，为保证列车运营的平稳性，建议钢轨最大垂向位移不超过1.5 mm。

另外，本文还采用自密实混凝土层和路基层所受压应力评价系统的受力特性。

2.3 模型验证

当不考虑板端离缝，高速列车以300 km/h的速度通过CTTSⅢ型板式无砟轨道时，系统动力响应如图4所示。

本文仿真计算动力响应各指标最大值与相关文献仿真结果及实测结果的对比如表1所示。

从图1及表1可知，本文计算结果与相关文献动力响应曲线吻合较好，且动力响应最大值量级相当，说明本文模型正确可靠，可用于研究板端离缝对CRTSⅢ型板式无砟轨道动力响应的影响。

表1 本文仿真结果与相关结果对比

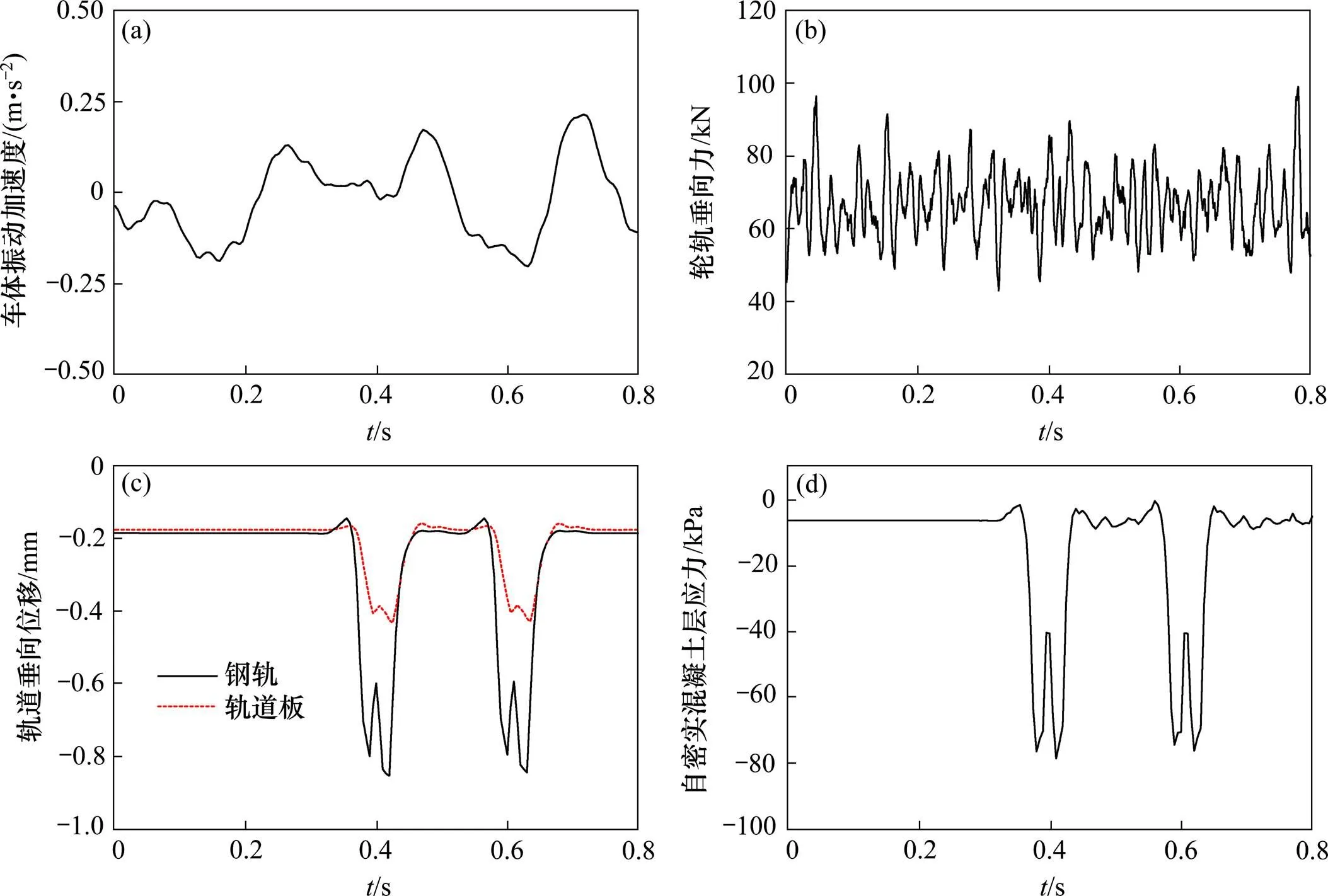
(a) 车体振动加速度；(b) 轮轨垂向力；(c) 轨道结构位移；(d) 自密实混凝土层压应力

3 板端离缝对系统动力性能的影响

根据相关现场调研可知，CRTSⅢ型板式无砟轨道的轨道板与自密实混凝土层的层间离缝主要发生在板端，且极易沿横向贯穿[9]。因此，本文假定板端离缝沿轨道板横向完全脱空。在距离模型左端56.7 m处设置板端离缝，利用建立的列车-CRTSⅢ型板式无砟轨道−路基垂向耦合振动模型，通过修改相关参数，分析了不同层间离缝长度下系统的动力特性。考虑最不利的影响，假定板端离缝至扣件的正下方，板端离缝长度分别取为0，0.28，0.91，1.54，2.17，2.8和3.43 m，列车运营速度为300 km/h。考虑篇幅限制，本文主要对不同离缝长度下动力响应的最大值进行分析。

3.1 车辆系统动力特性

不同板端离缝下车体和转向架的振动加速度随板端离缝长度的变化如图5所示。

从图5可见，随着板端离缝长度的增大，车体和转向架的垂向加速度均增大。当CRTSⅢ型板式轨道板端未发生离缝时，车体和转向架的垂向加速度分别为0.216 m/s2和1.941 m/s2；板端离缝长度增大至3.43 m时，车体和转向架的垂向加速度分别为0.267 m/s2和3.728 m/s2，分别增大23.61%和92.06%。当板端离缝长度增大至2.17 m时，车体和转向架的垂向振动加速度明显增大，但车体的垂向加速度仍小于舒适度标准0.13。

不同层间离缝长度下，轮轨垂向力及减载率如表2所示。

从表2可见，轮轨垂向力和减载率均随着板端离缝长度的增大有增大的趋势，但变化幅度均较小，轮轨垂向力未超过170 kN的限值，减载率未超过限值0.9。

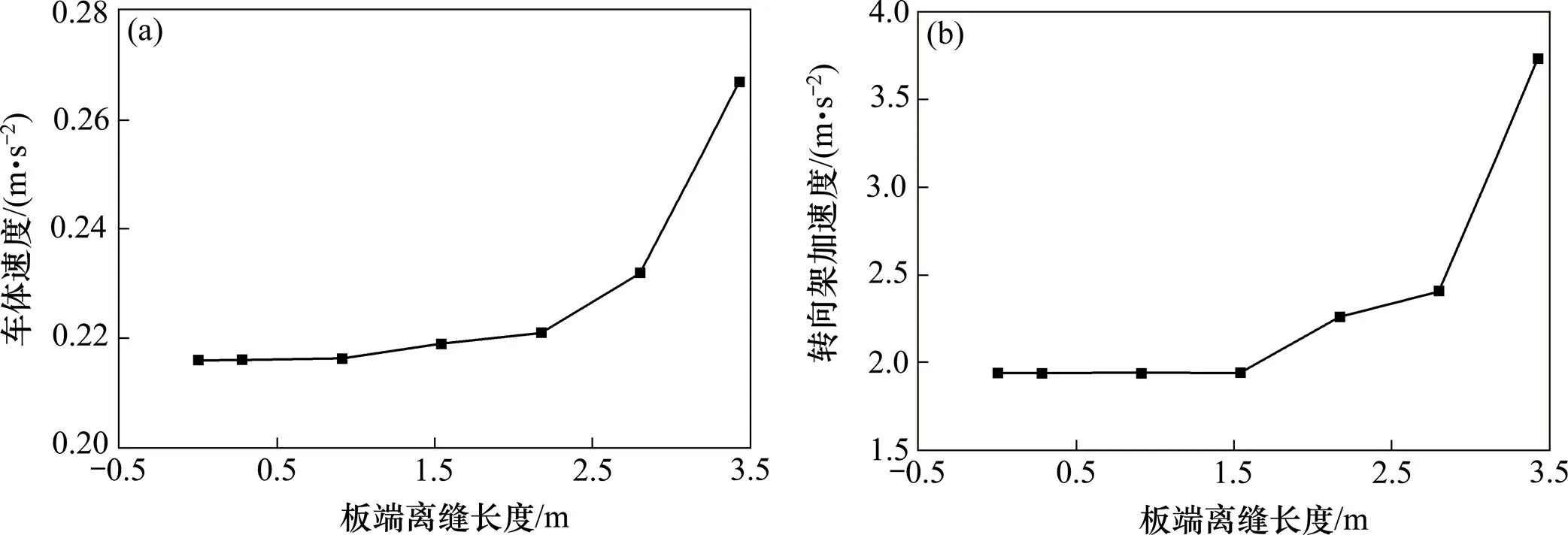
(a) 车体；(b) 转向架

表2 轮轨垂向力和减载率

3.2 轨道系统动力特性

钢轨垂向位移随层间离缝长度的变化如图4所示。从图6可见，钢轨垂向位移和轨道板垂向位移随板端离缝长度增大而增大，而底座板的垂向位移则减小。这是由于轨道板与自密实混凝土层产生离缝后，随着离缝长度的增大，列车荷载传递至底座板的荷载越小，从而导致离缝区底座板的垂向变形减小。当板端离缝长度未超过1.54 m时，钢轨垂向位移变化平缓且小于1.5 mm；当层间离缝长度超过1.54 m时，钢轨垂向位移急剧增大；当离缝长度达到3.43 m时，钢轨垂向位移达到3.93 mm，相比未离缝时的钢轨垂向位移增大3.6倍。

最大扣件上拔力随板端离缝长度的变化如图7所示。

从图7可见，扣件系统最大上拔力随板端离缝长度增大而增大。当板端未发生离缝时，扣件上拔力为1.08 kN，当板端离缝长度达到1.54 m时，扣件上拔力达到9.41 kN，为正常情况的8.71倍，接近允许值10 kN，有可能造成扣件系统的零部件 破坏。

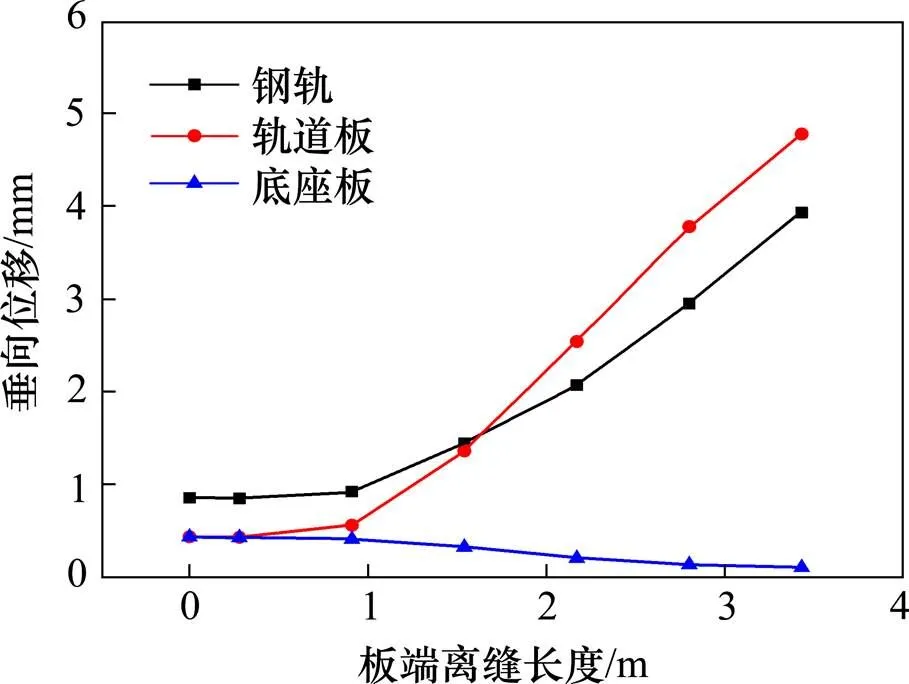
图6 轨道结构位移随离缝长度的变化规律

不同板端离缝长度下，离缝处自密实混凝土层所受压应力及路基表面压应力如表3所示。从表3可知，自密实混凝土层所受压应力随着板端离缝长度的增大而增大，路基表面压应力则随板端离缝长度的增大而减小。由于本文选取板端离缝正下方路基层的受力，故路基层所受压应力随着板端离缝长度的增大而降低。当板端离缝长度增大至1.54 m时，自密实混凝土层压应力为2 339.24 kPa，增大了28.75倍；路基表面压应力为27.93 kPa，降低了22.78%。在列车动荷载作用下，将形成“自密实混凝土层受力增大−自密实混凝土层破损−板端离缝加剧”的恶性循环，从而影响CRTSⅢ型板式无砟轨道的耐久性。

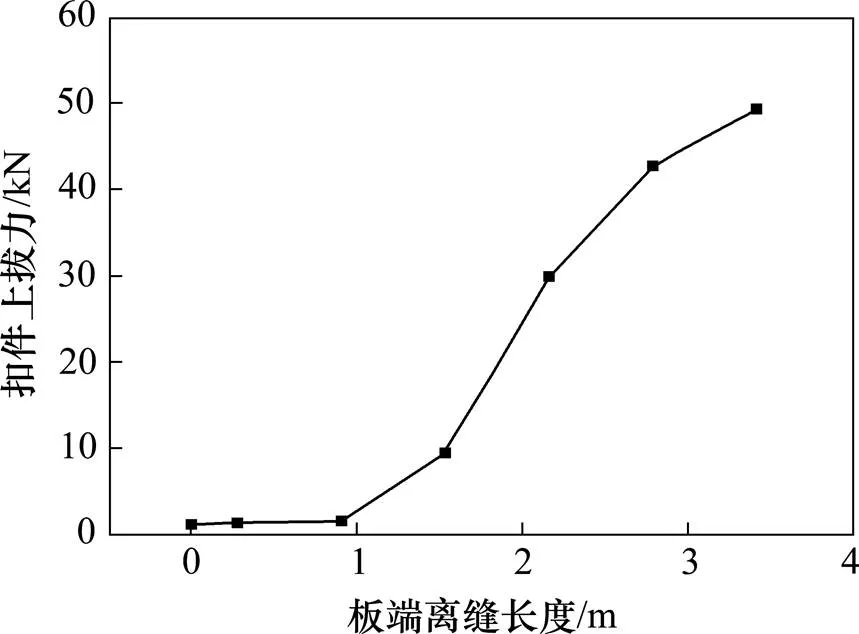
图7 扣件系统最大上拔力

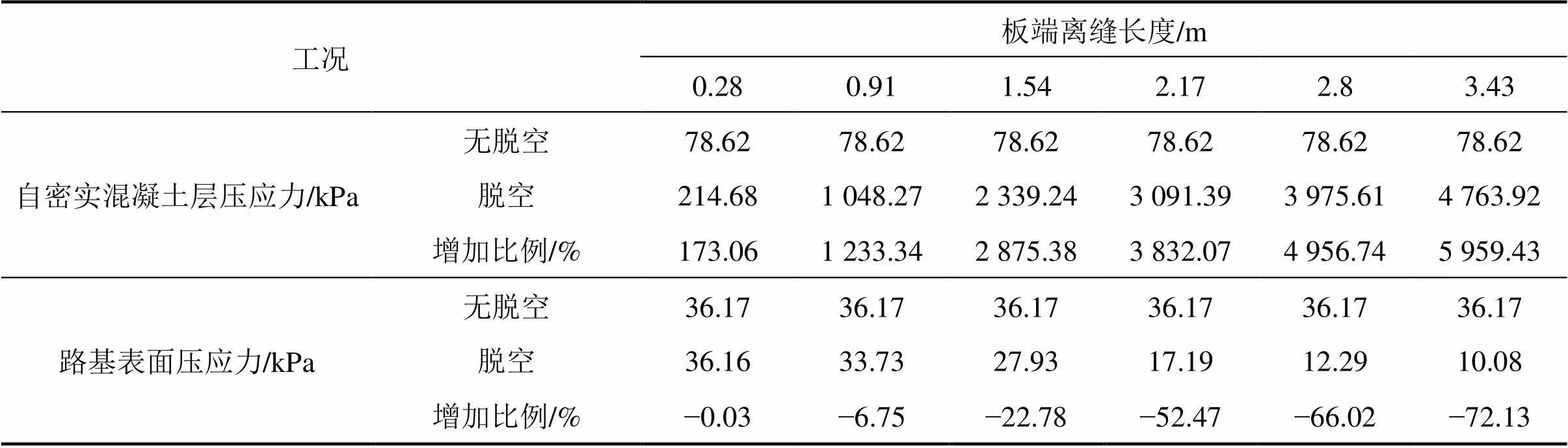
表3 离缝区域自密实混凝土层压应力及路基表面压应力

通过以上分析可知，考虑到板端离缝长度超过1.54 m以后，轨道系统的垂向位移出现拐点、扣件系统上拔力接近允许值、自密实混凝土层压应力也较无脱空时增大28.75倍，因此建议CRTSⅢ型板式无砟轨道的板端离缝长度不宜超过1.54 m。

4 结论

1) 板端离缝长度增大将导致车辆和转向架振动加速度增大，但板端离缝长度不大时不会影响行车的舒适性。

2) 板端离缝长度对轨道结构位移、扣件系统上拔力和自密实混凝土层压应力影响显著，当脱空长度达到1.54 m时，钢轨垂向位移、扣件系统上拔力和自密实混凝土层压应力较无离缝时分别增大3.6倍、8.71倍和28.75倍。

3) 轨道板与自密实混凝土层板端发生离缝将减弱列车荷载向下部结构的传递，因此，板端离缝区域下底座板的位移及路基应力较无脱空时均会减小。

4) 综合考虑板端离缝长度对行车安全性和轨道系统动力响应的影响，建议轨道板与自密实混凝土层的板端离缝长度不宜超过1.54 m。

[1] 向俊, 赫丹, 曾庆元. 水泥沥青砂浆劣化对板式轨道动力学性能的影响[J]. 中南大学学报(自然科学版), 2009, 40(3): 791−796. XIANG Jun, HE Dan, ZENG Qingyuan. Effect of cement asphalt mortar disease on dynamic performance of slab track[J]. Journal of Central South University (Science and Technology), 2009, 40(3): 791−796.

[2] LIU Dan, LIU Yufeng, REN Juanjuan, et al. Contact loss beneath track slab caused by deteriorated cement emulsified asphalt mortar: Dynamic characteristics of vehicle-slab track system and prototype experiment[J]. Mathematical Problems in Engineering, 2016, 2016(3): 1−12.

[3] REN Juanjuan, YANG Rongshan, WANG Ping, et al. Influence of contact loss underneath concrete underlayer on dynamic performance of prefabricated concrete slab track[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit, 2017, 231(3): 1−8.

[4] WANG Ping, XU Hao, CHEN Rong. Effect of cement asphalt mortar debonding on dynamic properties of CRTS II slab ballastless track[J]. Advances in Materials Science & Engineering, 2014, 2014(2): 1−8.

[5] 李培刚, 刘学毅, 黎国清. CA砂浆脱空对桥上单元板式轨道动力特性的影响研究[J]. 中国铁道科学, 2014, 35(3): 20−27. LI Peigang, LIU Xueyi, LI Guoqing. Influence of CA mortar void on dynamic characteristics of unit slab track on bridge[J]. China Railway Science, 2014, 35(3): 20−27.

[6] 杨荣山, 刘克飞, 任娟娟, 等. 砂浆伤损对轮轨系统动力特性的影响研究[J]. 铁道学报, 2014, 36(7): 79−84. YANG Rongshan, LIU Kefei, REN Juanjuan, et al. Research on effect of cement asphalt mortar damages on dynamic characteristics of wheel-rail system[J]. Journal of the China Railway Society, 2014, 36(7):79−84.

[7] 周毅. CRTSⅢ型板式轨道减振特性研究[D]. 成都: 西南交通大学, 2011. ZHOU Yi. Research of vibration damping characteristics of CRTSⅢ slab track[D]. Chengdu: Southwest Jiaotong University, 2011.

[8] 张丽平. 桥上CRTSⅢ型板式无砟轨道动力学性能分析[D]. 成都: 西南交通大学, 2011. ZHANG Liping. The dynamic performance analysis of CRTSⅢslab track on bridge[D]. Chengdu: Southwest Jiaotong University, 2011.

[9] 杨政. CRTSⅢ型板式轨道层间离缝下的受力及维修限值研究[D]. 成都: 西南交通大学, 2014. YANG Zheng. CRTSⅢ型板式轨道减振特性研究[D]. Chengdu: Southwest Jiaotong University, 2014.

[10] Popp K, Kaiser I, Kruse H. System dynamics of railway vehicles and track[J]. Archive of Applied Mechanics, 2003, 72(11/12): 949−961.

[11] ZHAI W, WANG K, CAI C. Fundamentals of vehicle- track coupled dynamics[J]. Vehicle System Dynamics, 2009, 47(11): 1349–1376.

[12] 翟婉明. 车辆−轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015. ZHAI Wanming. Coupling dynamics of vehicle-track system[M]. 4th ed. Beijing: Science Press, 2015.

[13] 中国铁道科学研究院. 盘锦至营口客运专线CRTSⅢ型板式无砟轨道系统动力性能试验研究[R]. 北京: 中国铁道科学研究院, 2013. China Academy of Railway Sciences. Dynamic performance test research on the CRTSⅢ type slab ballastless track of Panjin-Yingkou passenger dedicated line[R]. Beijing: China Academy of Railway Sciences, 2013.

[14] 王成晓. CRTSⅢ型板式无砟轨道力学特性研究[D]. 北京: 北京交通大学, 2011. WANG Chenxiao. Study on mechanical charateristics of CRTSⅢ type slab ballastless track[D]. Beijing: Beijing Jiaotong University, 2011.

Dynamic properties research of CRTSⅢslab track under slab ends cavity

LIU Ping1, WU Xin1, XU Hao2

(1. Department of Vehicle, Hebei Vocational College of Rail Transportation, Shijiazhuang 050000, China; 2. China Railway Eryuan Engineering Group Co. Ltd, Chengdu 610031, China)

The cavity between slab track and self-compaction concrete is one of the main damage types in the china railway track system(CRTS)Ⅲslab track, in order to analyze the influence of slab ends cavity on the dynamic properties of CRTSⅢslab track, a vertical coupling dynamical model of a vehicle-CRTSⅢslab track -subgrade system was established. And the effects of different lengths of slab ends cavity on dynamic response of the vehicle and track system were analyzed. The results show that the slab ends cavity increase the dynamic response of track. When the length of slab ends cavity exceed to 1.54 m, the vertical displacement of track appear inflection point, the uplift force of fastener system approach to 10 kN, and the vertical dynamic compressive stress of self-compaction concrete increase 28.75 times near the slab ends cavity area. Slab ends cavity lead the self-compaction concrete to degradation easily. It is suggested that repairing the slab ends cavity in time when the length of slab ends cavity reach to 1.54 m from the point of durability of ballastless track.

CRTSⅢslab track; slab ends cavity; high speed train; dynamic response; maintenance

U213.2

A

1672 − 7029(2019)10− 2395 − 07

10.19713/j.cnki.43−1423/u.2019.10.002

2018−12−28

河北省自然科学基金资助项目(E2017001216)

徐浩(1989−)，男，湖北天门人，高级工程师，博士，从事轨道结构及静、动力学研究；E−mail：xhao0@163.com

(编辑 阳丽霞)