双层泡沫铝夹芯板抗冲击性能数值研究

邓旭辉，李亚斌

双层泡沫铝夹芯板抗冲击性能数值研究

邓旭辉，李亚斌

(湘潭大学 土木工程与力学学院，湖南 湘潭 411105)

泡沫铝材料具有轻质高强和吸能比高等特性常用于抗爆结构。为研究双层泡沫铝夹芯板在冲击荷载下的动力学响应，建立TNT炸药-双层泡沫铝夹芯板-空气的三维有限元模型，采用ALE多物质流固耦合算法分析双层泡沫铝板在冲击荷载作用下的弹塑性变形机理、能量吸收特性。研究结果表明：在相同加载条件下，双层泡沫铝夹芯板要比单层泡沫铝夹芯板有着更强的抗冲击性能；随着面板厚度的增加，泡沫铝板在冲击荷载作用下的塑性变形明显减小，结构的整体安全性增加，但是整体吸能缺减小；上层面板与上夹芯层占结构总吸能较大；正梯度板结构要优越于相同厚度的面板结构，为设计优质抗冲击双层泡沫铝板提供参考依据。

泡沫铝；双层夹芯板；爆炸荷载；能量吸收特性；数值仿真

泡沫铝作为一种新型多孔材料具有相对密度轻、强度高、吸能比高等优良特性的新型工程材料，越来越多地被用于抗爆结构。其工作机理是当夹芯结构受到冲击荷载，夹芯产生压缩变形，从而吸收大量的能量，进而能够抵抗较大的能量冲击[1-4]。其优异的结构特性引起了国内外学者的广泛关注。Vaziri等[5]比较了金属夹层板与相同重量的实心板的抗冲击性，发现夹层板在冲击载荷下表现出优异的机械性能。Radford等[6]对面板为钢板、泡沫芯层为铝合金的夹芯板进行了冲击实验和有限元模拟，结果表明泡沫铝结构能耗散更多的冲击能量从而减少后面板的挠度，增加面板或芯层的厚度均能提高整体的抗形变能力。倪小军等[7]研究泡沫铝在爆炸冲击作用下的结构特性数值研究，结果证明所建立的泡沫铝的流体弹塑性本构方程可以用来描述泡沫铝的冲击特性，这为研究泡沫铝结构提供了理论基础。爆炸实验是检验结构抗爆性能最有效、最直接的方法，但其耗费资源巨大并存在风险。数值模拟是现代一种流行的科学手段，这种方法能够有限的还原实验现象，获得冲击荷载下结构变形过程和损伤机理[8−10]，且具备节省时间、成本的优势。本文研究双层泡沫铝复合结构在冲击荷载下的变形机理和能量吸收特性。数值模拟得出在冲击荷载下泡沫铝结构后面板中心点位移、夹芯总能量时程曲线，然后据此分析不同时间段面板、夹芯泡沫铝的动力学行为以及各个阶段的能量吸收特性。考虑不同结构参数对结构响应的影响，分析双层泡沫铝板面板厚度、不同爆轰入射角、面板厚度配合对结构响应的影响，这为后续双层泡沫铝板设计提供定量依据。

1 数值模拟方法与材料参数

1.1 流固耦合算法

流固耦合算法是通过一定的约束方法将结构与流体耦合在一起,实现力学参量的传递。其广泛应用于各种爆炸(水下、空中、建筑物和土壤中)、气囊的展开、体积成型、罐内液体晃动等[11]分析中。主要的约束方法有：速度约束、加速度约束和罚函数约束。流固耦合算法的优点在于行有限元网格划分时，不需要耦合面上的流体单元和结构单元一一对应，很大程度上减少了计算的工作量。在流流固耦合分析中，常用的约束方法是速度加速度约束，其计算步骤为：

1) 搜寻包含结构节点的流体单元，将结构单元节点参数(质量、动量、节点力)分配给流体单元 节点

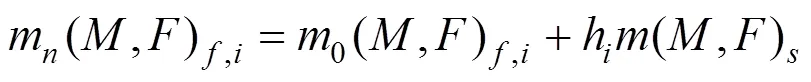
2) 计算新的流体节点加速度(速度)

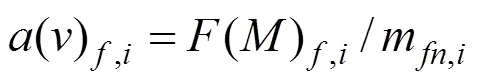
3) 约束结构节点的加速度(速度)

式中：m和0分别为分配前后流体单元节点质量；和分别为动量、节点力；和为节点加速度和速度；为单个流体单元中包含的节点数；和为流体和实体单元符号；为节点编号，代表分配后的节点。

1.2 材料模型

1.2.1 炸药材料

本文模拟炸药选用高性能炸药，结合JWL状态方程来描述爆炸时候产生的高压应力波，JWL状态方程的-关系以及各个参数的意义如下：

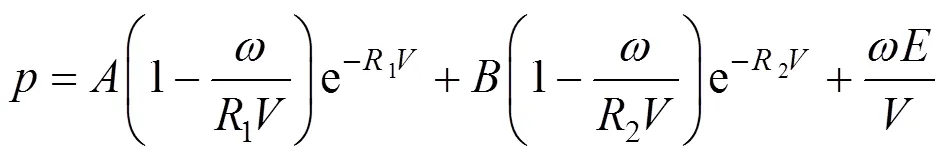
TNT炸药的参数见本文参考文献[12]，分别定义如下，为压强，为炸药体积，炸药密度为=1.73 g/cm3，爆速=0.753 cm/μs，爆压0.19 GPa，初始能量密度=6.93 GJ/m3，材料常数=373.8 GPa，=3.747 GPa，1=4.5，2=0.9，=0.35。

为了计算方便把空气视为理想气体[13]，具体状态方程如下：

其中状态方程参数分别为；g单位质量空气压强，空气密度g=0.00 1225 g/cm3，空气单位质量内能g=206.8 kJ/g，绝热指数=1.4。

1.2.2 泡沫铝材料

泡沫铝芯层采用可压缩泡沫材料模型，具体材料参数参考文献[14]，泡沫铝密度g=0.288 8 g/cm3，弹性模量1=330 MPa，准静态的应力应变曲线如图1。面板采用5052H112铝合金，采用塑性随动强化模型来描诉面板在受冲击下的变形。材料参数参考文献[14]，其中密度g=2.68 g/cm3，弹性模量2=66 GPa，断裂应力=227 MPa。

图1 泡沫铝准静态应力应变曲线

2 数值仿真分析

2.1 有限元计算模型

考虑炸药在双层泡沫铝中心点正上方200 mm处结构的整体响应。整个夹芯板的尺寸2×2=420 mm×420 mm，炸药冲击面积2×2=400 mm×400 mm，夹芯层高度=30 mm，面板厚为为1 mm，双层泡沫铝板采用面板−芯层−面板−芯层−面板的模式，由于整个结构的对称性，因此仅对面板的1/4进行了建模，目的可以大大减少运算时间提高运算效率。TNT、空气、泡沫铝夹芯单元采用8节点实体单元，面板与属于薄板结构故采用薄板4节点单元，计算时间为 2 000 μs，接触类型分别为前面板与上芯层、上芯层与中面板、中面板与下芯层、下芯层与后面板，板层之间均定义为自动面面接触，约束类型采用上面板与下面板边界10 mm宽的边界面采用固定约束，本模拟的边界条件为：空气域模型所有外部节点构成的节点组使用非反射边界条件，并采用吸收膨胀波和剪切波的方法以保证冲击波不会在空气域边界发生反射，减小模拟误差。

图2 整体有限元模型

图3 结构的有限元模型

图4 泡沫铝板的几何尺寸

表1 实验值[14]与模拟值后面板中心点位移对比

2.2 数值仿真与实验的效验

参照文献[14]模拟方案，模拟该文献中的单层泡沫铝的实验工况。数值模拟得出夹芯结构在不同炸药当量冲击下后面板中心的残余变形量如表1，其表明数值模拟数据与实验数据平均误差不超6.7%，图5显示在数值计算结束后整个单层泡沫铝结构的变形形状与实验图相似，证明本文所建的有限元模型和使用的算法的有效性。在实验的基础上本文考虑双层的泡沫铝板，研究双层泡沫结构在冲击荷载下的变形机理与能量吸收特性。

图5 实验图与模拟图变形对比

单位：102 GPa

2.3 夹芯板的变形机理与能量吸收特性

2.3.1 冲击荷载下双层泡沫铝板的变形机理

图6显示了180 gTNT距离中心200 mm面板厚度1.0 mm夹芯高度30 mm(上层与下层各15 mm)引爆后结构的响应过程。爆点起爆后到结构最后响应结束，大概分为3个阶段，第1阶段0~50 μs；爆轰产物在空气中的传播阶段，TNT瞬间产生高压应力波并瞬速以球形的状态向外传播，图7(30 μs)清楚地显示了爆炸冲击波以球形式扩展。起爆后如图6所示在50 μs左右时高压冲击波首先传播到双层泡沫铝板的上面板的中心。第2阶段50~80 μs；爆轰产物与结构的相互作用阶段；在50 μs时，上面板因冲击波的到来开始产生较大应力并带有弹性变形，上面板的变形导致上夹芯层的压缩变形趋于致密化，与此同时下夹芯层发生少量的压缩变形并带动下面板以相对于上面板较小的速度向下移动，并且随着冲击波的继续传递，变形由中心向外和向下延伸，80 μs时上层核心与下层核心总能量(动能与塑性变形能)分别为630 J和382 J。第3阶段80~2 000 μs；这一阶段，TNT与结构的相互作用已经消失，整个结构在惯性的作用下继续向下移动。此阶段，整个夹芯层开始凹陷压溃变形并逐渐细密化，由图8面板位移时程曲线可知在210 μs夹芯层压缩达到最大值，与此同时前后面板速度开始趋于一致，带动下面板一起向下变形，当变形区域延伸到边界固定区域时，发生全局的凹陷变形。随着弹性应变能的释放结构产生了负向加速度，由图8所示的面板位移减少阶段显示，开始全局的轻微震荡，最后恢复到静止状态，整个响应结束。图9夹芯层能量时程曲线得出响应结束后上层核心与下层核心总能量分别为423 J和196 J。由于结构局部弹塑性卸载，最终的残余变形会小于峰值变形。

图7为双层泡沫铝板有效应力等值线云图，在TNT炸药爆炸的瞬间，炸药在极短的时间内体积急剧膨胀，迅速由固态变为高温高压的气态，呈球形向外扩张。本次模拟采用流固耦合算法来处理TNT与双层泡沫铝板耦合关系，在=50 μs时应力波达到结构中心，由于设置的非法反射边界条件，冲击波不会在空气域边界发生反射(=160 μs)，冲击波与结构相互作用采用流固耦合中的常用的速度加速度约束，随着冲击波与结构的耦合作用其超压峰值被消弱(=300 μs)。此时结构的变形还在继续但是变形的程度减缓，最终结构的变形在=1 250 μs时基本定型。从有效应力等值线云图中可以得出结构正冲击面中心区域的应力比周围大的多并且应力区域呈圆形向边界发散。

单位：102 GPa

图8 面板中心位移时程曲线

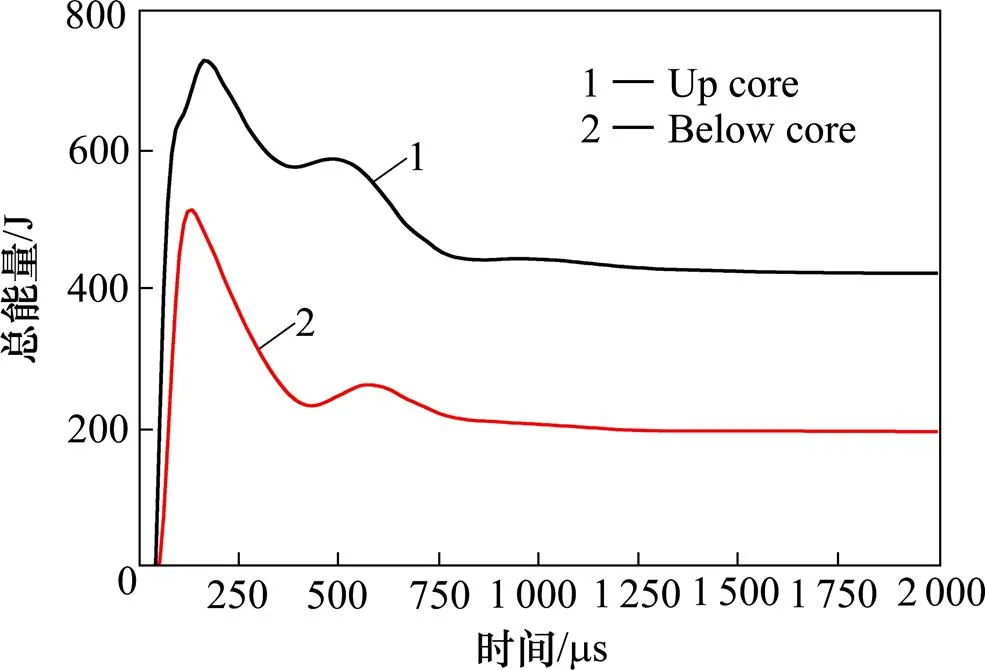
图9 夹芯层总能量时程曲线

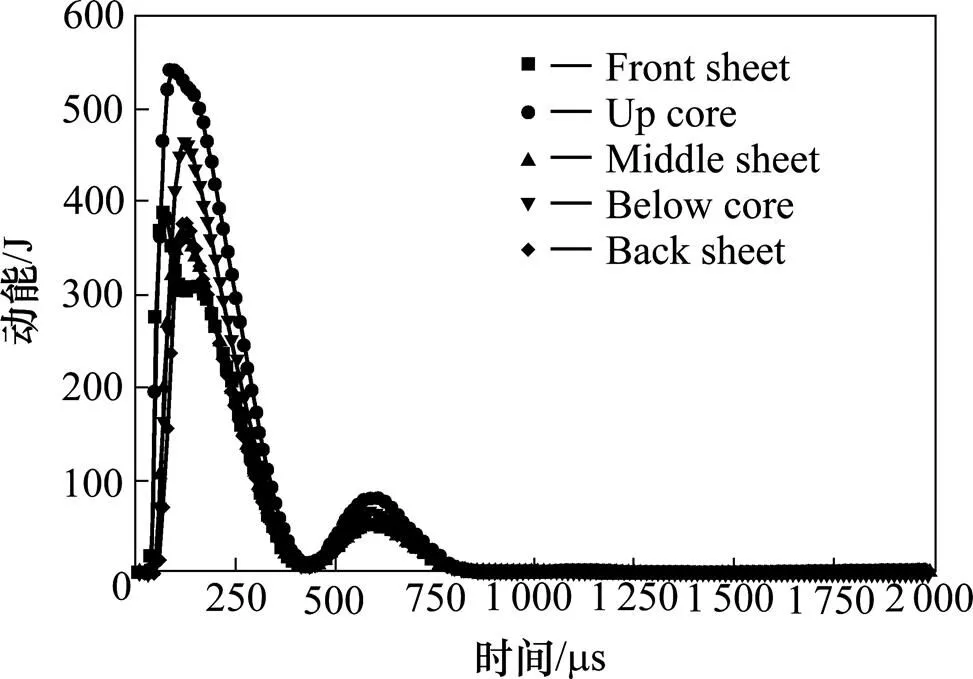
图10 双层泡沫铝板动能时程曲线

2.3.2 冲击荷载下双层泡沫铝板的能量吸收特性

为研究双层泡沫铝在受冲击荷载作用时的吸能特性，图10和图11分别描绘出冲击荷载作用下双层泡沫铝结构的动能与塑性变形能时程曲线。在结构最初受到高压冲击波时候，双层泡沫铝夹芯板速度快速增加，在800 μs时候整个结构的动能接近为0。结构真正发挥抗爆性能是在125 μs之后，即图10结构动能下降阶段，此阶段双层泡沫铝板通过自己塑性变形吸收能量实现一部动能转化为塑性能。由图11塑性变形能曲线可知前面板与上层夹芯塑性变形能最大其次是下层夹芯，因此在实际应用中适量增加前面板厚度与上芯层高度可以增强结构的整体抗爆性与吸能特性。

图11 双层泡沫铝板塑性变形能时程曲线

3 参量对结构抗爆性能的影响

3.1 不同面板厚度对双层泡沫铝板变形的影响

控制单一变量面板厚度，其余参量与3.3.1节相同，本次模拟对单双层泡沫夹芯结构进行对比分析。

图12为不同面板厚度对单双层泡沫铝面板残余变形的影响。如图所示，随着面板厚度的增加，面板的最终变形整体上越小，与此同时，泡沫夹芯的压缩量也在变小，但压缩量变化并不太明显；当面板的厚度从1 mm增加到2 mm的时候，单层泡沫铝结构前后面板的非弹性变形分别减少了19%和25.7%；双层泡沫铝结构前后面板的非弹性变形分别减少了23.1%和32.6%。另外比较面板厚度分别为1 mm和2 mm的单层与双层泡沫铝结构时，发现相对于单层泡沫结构双层泡沫结构就前后面板的非弹性变形而言，分别减少了8.3%，11.8%，13%和20.1%。以面板的非弹性变形作为抗爆性能的依据，数值模拟得出相同体积的泡沫铝夹芯板结构，双层的结构能够更有效地抵抗爆炸冲击，并且这种结构性能在控制结构高度不变的情况下随着面板厚度增加而增加，这为工业设计出质轻、高强抗爆结构提供参考。

图12 不同厚度面板中心点的位移

图13给出了不同面板厚度单层、双层泡沫铝夹芯板结构的能量吸收，随着面板厚度的增加，夹芯结构受到冲击荷载作用下，单层、双层泡沫铝板的面板与夹芯所吸收的能量均有所减小，这是因为面板的厚度越厚，整个夹芯结构整体性得到提高，在受到相同大小的冲击荷载下能体现更强的抗爆性能。对比图12和图13发现随着面板厚度增加面板的残余变形量较小，然而整体结构的吸能却在减小，在实际工程应用中要平衡两者的关系。比较面板厚度分别为1 mm和2 mm单层、双层泡沫铝板结构的总能量，发现双层泡沫铝结构夹芯层、面板的能量相对于单层泡沫铝结构分别减少了11%，11%与17%，41%，由此可知，面板越厚的双层泡沫铝板相比单层泡沫结构有着较强抗冲击性能。图14给出本次模拟的最小与最大面板厚度单层与双层泡沫结构耗能时程曲线，曲线显示在冲击作用初期当双层泡沫结构的总能量变化不大，结构真正显示出差异的时候是夹层压缩趋于致密阶段，整个能量变化在1 250 μs趋于平稳，这与图8位移变化趋于平稳一致。

图13 不同面板厚度结构能量吸收

图14 面板厚度为1 mm和2 mm结构的耗能时程曲线

3.2 面板厚度匹配对结构抗爆性能的影响

为研究面板厚度配合对结构抗爆性能的影响，在保证面板总厚度为3 mm不变的情况下，改变3层面板厚度的匹配，采用正交设计的方法具体匹配模式参考表2，计算结果图15，其中，和分别代表上中下面板的厚度，其余模拟参量与3.3.1节相同。以面板的残余变形和夹芯层的压缩作为评估结构抗爆性能的依据，计算结果表明前中面板较厚时候如工况1，结构的核心压缩越小，但是后面板中心点的位移比较大，但是容易导致后面面板的撕裂失效。正梯度性面板结构能够有效地抗击外冲击，模拟的10个工况中工况4效果更为明显，就核心压缩与面板中心点的位移相对工况8减少了2%，核心压缩减少了11%，更能够发挥整体结构的稳定性。这为双层泡沫结构的设计提供一定的参考价值。

表2 不同工况下的面板厚度

图15 不同面板厚度配合下的面板位移

3.3 爆轰入射角对双层泡沫结构响应的影响

对于结构碰撞或冲击而言，往往不同的方向的碰撞对结构的破坏影响也会不同，因此撞击点和撞击角度将是结构防护过程中不可忽视的因素。为了研究冲击入射角度对夹芯板响应的影响，现考虑0°角，17°角和28°角的不同方向冲击，其余参量与工况3.3.1节相同。如图16所示，相对与正面冲击，17°和28°入射角前面板与后面板中心点位移分别减少了12%，17.7%与42%，55%，核心压缩量也相应减少了51%和68%。数值模拟表明，与正面冲击而言较大的入射角对结构的中心的压缩有着很大的影响，这是因为在一定范围内入射角越大，作用在结构上的能量越小，一大部分能量消散在空 气中。

图16 不同入射角面板中心位移曲线

图17为不同入射角夹芯塑性变形耗能时程曲线。由图17可知，在120 μs之前，3种角度冲击下，夹芯结构的内能(塑性变形能)几乎一样，这是因为，在爆炸的最初瞬间，结构受到巨大的冲击，冲击波与结构在短时间内无法完成明显差异性的能量交换。在120~430 μs之间，夹芯在惯性的作用下压缩致密化塑性变性能继续增加，能量曲线也因冲击角度的不同发生分歧。在430~750 μs时间段，入射角17°和28°塑性变性能走势与正面冲击有差别，因为入射角的变化改变了结构所受最大冲击的位置，结构整体的回弹有所减小，导致夹芯层塑性变形能变化不明显。

图17 不同入射角核心塑性变形耗能时程曲线

4 结论

1) 通过数值模拟得出夹芯板在受到冲击荷载下的响应主要分为3个阶段，第1阶段：TNT引爆后产生高压冲击波以球形向外传播，当冲击波传到结构前面板时，前面板获得初始速度，此时夹芯与后面板处于静止状态。第2阶段：力的传递阶段，高压冲击波与前面板的相互作用，力传递到夹芯，夹芯开始出现压缩变形，此时后面板处于静止状态。第3阶段：后面板达到屈服应力发生整体的震荡直至结构静止。

2) 考虑不同面板组合下双层泡沫铝板的抗冲击性能，计算结果表明正梯度板的双层泡沫夹芯铝板要比相同面板厚度双层泡沫夹芯板的整体性更好，这为设计出轻质、高强抗冲击的双层泡沫铝板提供参考。

3) 对比分析相同面板厚度、核心高度的泡沫结构，在受到相同荷载的冲击下，双层泡沫铝夹芯板要比单层泡沫铝夹芯板体现更强的抗爆性能。

4) 随着面板厚度的增加，结构的后面板的非弹性变形降低，核心压缩越小但是夹芯层吸收能量降低，在实际工程中要注意平衡两者的关系。

5) 考虑不同的爆轰入射角，随着入射角的增加，结构所受的冲量减小导致双层泡沫铝板的各项变形都在减小，入射角越大这种效果越发明显，这为双层泡沫铝板在实际应用中的位置布置提供有限元基础。

[1] 杨冬丽, 王琳, 杨杰, 等. 泡沫铝复合结构的应力波防护性能研究[J]. 兵工学报, 2014, 35(1): 96−101.YANG Dongli, WANG Lin, YANG Jie, et al. Research on protective performance of foam aluminum composite structure against stress wave[J]. Journal of Ordnance Engineering, 2014, 35(1): 96−101.

[2] WANG Y, Liew J Y R. Blast performance of water tank with energy absorbing support[J]. Thin-Walled Structures, 2015(96): 1−10.

[3] LI S, WANG Z, WU G, et al. Dynamic response of sandwich spherical shell with graded metallic foam cores subjected to blast loading[J]. Composites Part A, 2014, 56(1): 262−271.

[4] 夏志成, 张建亮, 周竞洋, 等. 泡沫铝夹芯板抗冲击性能分析[J]. 工程力学, 2017, 34(10): 207−216. XIA Zhicheng, ZHANG Jianliang, ZHOU Jingyang, et al. Analysis of impact resistance of foamed aluminum sandwich panels[J]. Engineering Mechanics, 2017, 34(10): 207−216.

[5] Vaziri A, Hutchinson J W. Metal sandwich plates subject to intense air shocks[J]. International Journal of Solids & Structures, 2007, 44(6): 2021−2035.

[6] Radford D D, Mcshane G J, Deshpande V S, et al. The response of clamped sandwich plates with metallic foam cores to simulated blast loading[J]. International Journal of Solids and Structures, 2006, 43(7/8): 2243−2259.

[7] 倪小军, 马宏昊, 沈兆武, 等. 泡沫铝爆炸冲击特性的数值研究[J]. 爆炸与冲击, 2013, 33(2): 120−125. NI Xiaojun, MA Honghao, SHEN Zhaowu, et al. Numerical study on the impact characteristics of aluminum foam explosion[J]. Explosion and Shock Wave, 2013, 33(2): 120−125.

[8] Heimbs S, Schmeer S, Middendorf P, et al. Strain rate effects in phenolic composites and phenolic-impregnated honeycomb structures[J]. Composites Science & Technology, 2007, 67(13): 2827−2837.

[9] Mohan K, Yip T H, Idapalapati S, et al. Impact response of aluminum foam core sandwich structures[J]. Materials Science & Engineering A, 2011, 529(1): 94−101.

[10] 张培文, 李鑫, 王志华, 等. 爆炸载荷作用下不同面板厚度对泡沫铝夹芯板动力响应的影响[J]. 高压物理学报, 2013, 27(5): 699−703. ZHANG Peiwen, LI Xin, WANG Zhihua, et al. Influence of different panel thickness on dynamic response of foamed aluminum sandwich panel under explosive loading[J]. Chinese Journal of High Pressure Physics, 2013, 27(5): 699−703.

[11] 赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003. ZHAO Haoou. LS-DYNA dynamic analysis guide[M]. Beijing: Ordnance Industry Board Society, 2003.

[12] 于川, 李良忠, 黄毅民. 含铝炸药爆轰产物JWL状态方程研究[J]. 爆炸与冲击, 1999, 19(3): 274−279. YU Chuan, LI Liangzhong, HUANG Yimin. Study on JWL equation of state for detonation products of aluminized explosives[J]. Explosion and Shock Wave, 1999, 19(3): 274−279.

[13] 李翼祺, 马素贞. 爆炸力学[M]. 北京: 科学出版社, 1992. LI Yiqi, MA Suzhen. Explosive mechanics[M]. Beijing: Science Press, 1992.

[14] 王涛, 余文力, 秦庆华, 等. 爆炸载荷下泡沫铝夹芯板变形与破坏模式的实验研究[J]. 兵工学报, 2016, 37(8): 1456−1463.WANG Tao, YU Wenli, QIN Qinghua, et al. Experimental study on deformation and failure modes of foam aluminum sandwich panels under blast loading[J]. Journal of Ordnance Engineering, 2016, 37(8): 1456− 1463.

Numerical study on impact resistance of double-layer foam aluminum sandwich panels

DENG Xuhui, LI Yabin

(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)

Foamed aluminum material has the characteristics of light density and high strength and is often used in anti-explosion structures. In order to study the dynamic response of double-layer foam aluminum sandwich panels under impact loading, A three-dimensional finite element model of TNT explosives-double foam aluminum sandwich panel-air was established based on LS-DYNA nonlinear finite element software. The ALE multi- material fluid-solid coupling algorithm was used to analyze the deformation mechanism, plastic deformation and energy absorption of double-layer foam aluminum sheets under impact loading. The numerical simulation results show that the double-layer foam aluminum sandwich panel has stronger impact resistance than the single-layer foam aluminum sandwich panel; as the thickness of the panel increases, the plastic deformation of the bee foam aluminum panel under the impact load is significantly reduced. The overall safety of the structure is increased but the overall energy absorption is reduced; The upper panel and the upper sandwich layer account for a larger total energy absorption of the structure; the positive gradient thickness of the panel structure is superior to The same panel thickness structure, which provides a reference for designing high quality impact resistant double foam aluminum plates.

aluminum foam; double-layer sandwich panel; blast loading; energy absorption characteristics; numerical simulation

O385

A

1672 − 7029(2019)10− 2603 − 09

10.19713/j.cnki.43−1423/u.2019.10.029

2018−12−28

国家自然科学基金资助项目(51434002)

邓旭辉(1975−)，男，湖南郴州人，副教授，博士，从事工程结构设计与优化研究；E−mail：dengxh75@163.com

(编辑 蒋学东)