有限理性下物流配送路径决策研究

袁嘉杉，朱昌锋，张正坤

有限理性下物流配送路径决策研究

袁嘉杉，朱昌锋，张正坤

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

为研究物流企业在有限理性条件下的配送路径决策问题，在分析配送过程中恶劣天气和道路拥堵所可能造成损失的基础上，引入前景理论(Prospect Theory，PT)量化物流企业主观风险态度，构建以运输总成本和顾客满意度为决策属性的物流配送路径决策模型；通过模型评价得出前景值最大的物流配送路径方案，并对前景价值函数和主观概率函数中的参数以及决策模型的参照点进行了扰动分析。研究结果表明：基于PT的物流配送路径决策模型能够弥补期望效用理论的不足，使决策结果符合决策者有限理性的特征，依托该模型得到的最优配送路径，可以较大限度地减少不确定风险带来的损失及损失造成的心理落差。

物流配送路径；前景理论(PT)；区间概率；参数扰动

由于我国电子商务产业的迅猛发展，物流企业需要满足更多的物流配送需求。这就要求物流企业在配送方案的制定与选择方面，既要降低配送成本又要提高服务质量。而在物流配送方案决策过程中，配送路径会影响整个方案的优劣。因此，物流配送路径优化问题的研究就具有十分重要的理论意义与现实意义。目前，国内外的学者已经对物流配送路径优化问题进行了大量研究。吴聪等[1−3]分别设计了改进的自适应遗传算法、蚁群算法和基于混沌的粒子群算法对物流配送路径优化模型进行了求解；李延来等[4]提出了一种利用模糊互补判断矩阵判断方案优先度的物流方案评估方法；蒋国清等[5]构建了一种基于两阶段式的物流配送路径优化模型；李进等[6]基于碳排放交易机制，引入碳排放度量方法构建物流配送路径优化模型；Montané 等[7]构建了针对需要同时提供提货与交付服务的双向物流配送问题的路径优化模型，并设计禁忌搜索算法进行求解；Desrochers等[8]构建了带时间窗的物流配送车辆路径优化模型，并结合列生成算法与动态规划方法进行求解；Ootertag等[9]构建了带时间窗大规模多配送中心车辆路径优化模型，采用结合模拟算法(Mimetic Algorithm，MA)和POPMUSIC 算法的混合启发式算法进行求解。既有研究主要是从模型求解算法和影响约束条件的客观因素方面，对物流配送路径决策进行了优化和创新。但均未考虑决策者的主观风险态度对决策结果的影响，因为在实际决策过程中，决策者通常是有限理性的，因此，当决策者面对不确定风险可能带来的不同程度的损失时，其风险感知态度就会影响最优配送路径选择。鉴于此，拟引入前景理论(Prospect Theory，PT)量化决策者的风险偏好，构建基于PT的物流配送路径决策模型，以期从配送路径的Pareto解集中选择预期损失更少，更符合决策者心理预期的最优方案，提高物流企业的服务质量与配送效率。

1 物流配送决策属性分析

1.1 运输总成本

设[ETl,LTl]为期望送达时间窗，[ATl,BTl]为可容忍送达时间窗，tl为Nl的货物送达时间。则混合时间窗惩罚成本如图1所示。

则运输总成本1为：

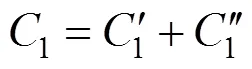
1.2 顾客满意度

顾客满意度随送达时间变化趋势如图2所示。

图2 顾客满意度变化趋势

在混合时间窗的情况下，对于顾客点N来说，在t时刻送达货物的满意度为：

1.3 物流配送风险分析

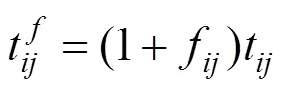
2 基于PT的配送方案决策模型

PT通过考虑决策人有限理性和参照点依赖的决策特征，弥补了期望效用理论仅考虑效用最大化的缺陷，其主要由前景价值函数和主观概率函数组成。

2.1 前景价值函数

设R为属性C的参照点，选取均值做为参照点，则参照点R为：

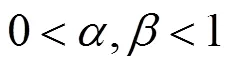
2.2 主观概率函数

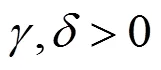
2.3 配送方案综合前景值

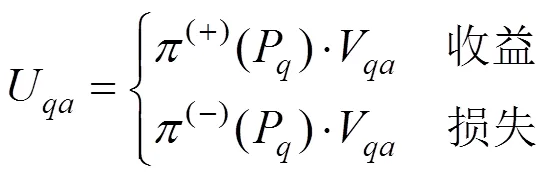
设1和2分别为1和2的属性权重，1+2=1，则方案A的综合前景值U为：

最后，比较所有方案的综合前景值U，其中前景值最大的方案为最优方案。

3 实例分析

3.1 数据及计算过程

根据文献[12]的数据及物流配送模型，运用遗传算法解得上海市37个苏宁门店配送问题的Pareto解集，配送方案内容见表1。

表1 配送方案Pareto解

首先，根据式(1)~(9)计算4个方案的属性值并根据式(10)确定参照点，结果见表2。

然后，根据式(11)和式(12)计算各方案中各属性前景价值函数的值，并根据式(13)~(17)确定方案主观概率，结果见表3。

表2 属性值及参照点

表3 前景价值及主观概率

最后，根据式(18)~(20)计算各备选方案综合前景值，1=2=0.5，结果见表4。

表4 综合前景值

对比4个方案的综合前景值，4>1>3>2，因此，选择方案4为最优配送方案。

为了对比运用前景理论和期望效用理论所得到最优方案间的差异，分别计算出4个备选方案的前景值和期望值，结果见表5。

由表5可知，运用前景理论和期望效用理论得到的最优方案均为4。从期望值来看，由于4的总成本低于1，而1的满意度高于4，因此，1和4的期望值相差不大。但从前景值来看，对于总成本，1和4相较于参照点均为收益，其中4的收益值和主观概率均较大，更符合决策者在有限理性状态下，面对收益呈现风险规避的特征；对于满意度，1为收益而4为损失，1的主观概率大于4，因此，1符合收益状态下的风险规避特征，而4符合损失状态下的风险追寻特征。综上所述，虽然在此算例中运用前景理论和运用期望效用理论得到的最优方案相同，但运用前景理论得到的最优方案与次优方案间的前景值差异比期望值差异更明显，说明前景理论可以弥补期望效用理论未考虑决策者有限理性特征的不足，更符合决策者的主观风险感知态度。

表5 前景值与期望值

3.2 参数扰动分析

3.2.1 风险态度系数和扰动分析

由图3可以看出，1和4的综合前景值仅随着的增加而增加，不受影响。而2和3的综合前景值同时随和的增加而减小。1和4的总成本均为收益，尽管4的满意度为损失，但其主要趋势依旧随着的增加而增加；2和3的总成本均为损失，尽管其满意度均为收益，但其依旧主要随着的增加而减小，并在方向有小幅的递减。综上所述可得到以下2点结论：1) 当总成本为收益时，前景值与的值成呈相关；当总成本为损失时，前景值与的值呈负相关；当满意度为收益时，前景值与的值呈负相关；当满意度为损失时，前景值不受值影响；2) 在总成本和满意度2个决策属性中，总成本对方案前景值的变化趋势影响更大，满意度仅在其对应的变化趋势上产生小幅变化。

3.2.2 感知概率系数和扰动分析

由图4可以看出，方案1的综合前景值仅随的增加而减少，不受的影响；方案2，3和4的综合前景值均随的增加而减少，的增加而增加。结合各方案属性值的收益和损失情况分析可知，因为方案1的总成本和满意度均为收益，因此其主观概率仅随变化，不受的影响。而方案2，3和4的属性值均为一个收益另一个损失，因此其前景值受到和的共同影响，且随变化的程度大于随变化的程度。综上所述可得到以下2点结论：1) 当有某一属性值收益时，方案前景值就会受到的影响；当有某一属性值损失时，方案前景值就会受到的影响；2) 当和共同影响方案前景值时，的灵敏度大于的灵敏度。

(a) 方案A1；(b)方案A2；(c)方案A3；(d)方案A4

(a) 方案A1；(b)方案A2；(c)方案A3；(d)方案A4

3.2.3 参照点扰动分析

由表6可以看出，参照点选取依据的变化，会导致最优方案结果的不同，不同依据的参照点代表决策者内心不同的期望。而每一种参照点所选出的最优方案，都代表其在对应的期望情况下能够产生更少的损失及更小的心理落差。例如，当以最优点为参照点时，即将各方案中的最低的总成本和最高的满意度作为参照点，而所选出的最优方案1虽然其属性值均不为最优，但综合来看其相对于参照点可能造成的损失和心理落差更小，更符合决策者的主观风险态度。因此，在决定参照点的选取依据时，应当首先明确决策者的心理预期，再选择相应的参照点。

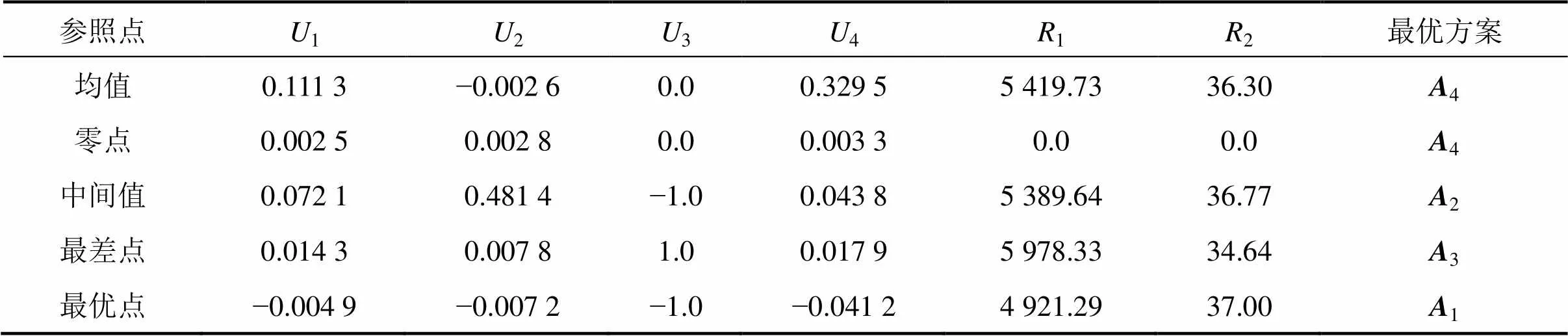
表6 参照点扰动分析

4 结论

1) 基于PT的物流配送方案决策模型得到的最优方案，能够弥补期望效用理论的不足，更符合决策者有限理性和参照点依赖的特征；在实际物流配送过程中，能够较大限度的减少恶劣天气和道路拥堵带来的损失，减少损失带给物流企业和顾客的心理落差。

2) 当运输企业决策人的风险态度发生改变时，运输总成本对方案前景值的影响大于顾客满意度的影响。

3) 在实际物流配送过程中，配送中心可能不止一个，因此，下一步的研究重点为PT与多配送中心−多顾客点物流配送路径优化问题的结合。

[1] 吴聪, 陈侃松, 姚静. 基于改进自适应遗传算法的物流配送路径优化研究[J]. 计算机测量与控制, 2018, 26(2): 236−240. WU Cong, CHEN Kansong, YAO Jing. Study on optimization of logistics distribution route based on improved adaptive genetic algorithm[J]. Computer Measurement & Control, 2018, 26(2): 236−240.

[2] 张勇. 基于改进蚁群算法物流配送路径优化的研究[J]. 控制工程, 2015, 22(2): 252−256. ZHANG Yong. Study of optimizing logistic distribution routing based on improved ant colony algorithm[J]. Control Engineering of China, 2015, 22(2): 252−256.

[3] 王铁君, 邬月春. 基于混沌粒子群算法的物流配送路径优化[J]. 计算机工程与应用, 2011, 47(29): 218− 221. WANG Tiejun, WU Yuechun. Study on optimization of logistics distribution route based on chaotic PSO[J]. Computer Engineering and Applications, 2011, 47(29): 218−221

[4] 李延来, 应程铄. 基于多种偏好信息的物流方案评估方法[J]. 计算机工程与应用, 2017, 53(17): 229− 233. LI Yanlai, YING Chengshuo. Evaluation approach of logistics schemes based on multi-format information [J]. Computer Engineering and Applications, 2017, 53(17): 229−233.

[5] 蒋国清, 潘勇, 胡飞跃. 两阶段式的物流配送路径优化方法[J]. 计算机工程与应用, 2015, 51(2): 255− 258, 264. JIANG Guoqing, PAN Yong, HU Feiyue. Research on logistics distribution route based on genetic algorithm and ant colony optimization algorithm[J]. Computer Engineering and Applications, 2015, 51(2): 255−258, 264.

[6] 李进, 张江华. 碳交易机制对物流配送路径决策的影响研究[J]. 系统工程理论与实践, 2014, 34(7): 1779− 1787. LI Jin, ZHANG Jianghua. Study on the effect of carbon emission trading mechanism on logistics distribution routing decisions[J]. Systems Engineering-Theory & Practice, 2014, 34(07): 1779− 1787.

[7] Montané F A T, Galvao R D. A tabu search algorithm for the vehicle routing problem with simultaneous pick-up and delivery service[J]. Computers & Operations Research, 2006, 33(3): 595−619.

[8] Desrochers M, Desrochers J, Solomon M. A new optimization algorithm for the vehicle routing problem with time[J]. Windows Operations Research, 1992, 40(10): 342−354.

[9] Ootertag A K, Doerner F, HARTL R F, et al. POPMUSIC for a real-world large-scale vehicle routing problem with time windows[J]. Journal of the Operational Research Society, 2009, 60(8): 934−943.

[10] 赵敏, 弓箭峰, 王利东. 基于前景理论的灰区间语言变量随机多属性决策模型[J]. 统计与决策, 2017(23): 45− 48. ZHAO Ming, GONG Jianfeng, WANG Lidong. Stochastic multiple attribute decision-making model of grey interval linguistic variable based on prospect theory[J]. Statistics & Decision, 2017(23): 45−48.

[11] 王奕璇, 陈荔, 王涛. 基于改进智能水滴算法的混合时间窗电商物流路径优化研究[J]. 科技管理研究, 2018, 38(11): 211−218. WANG Yixuan, CHEN Li, WANG Tao. Research on mixing time window e-commerce logistics route optimization based on improved intelligent water drop algorithm[J]. Science and Technology Management Research, 2018, 38(11): 211−218.

Research on decision of logistics distribution path under bounded rationality

YUAN Jiashan, ZHU Changfeng, ZHANG Zhengkun

(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to study the distribution route decision problems for logistics enterprises under the condition of bounded rationality, the Prospect Theory (PT) was introduced to quantify the subjective risk attitude of logistics enterprises on the basis of analyzing the possible losses caused by bad weather and traffic congestion in the process of distribution. A logistics distribution route decision model regarding total transportation cost and customer satisfaction as decision attributes was constructed. The model was used to evaluate and obtain the logistics distribution route schemes with the largest prospect value. The sensitivity analysis of parameters of prospect value function and subjective probability function and the reference points of decision model were conducted. The results show that the decision model of logistics distribution route based on PT can make up the deficiency of expected utility theory and make the decision result accord with the characteristic of bounded rationality. The optimal distribution route schemes obtained by this model can greatly reduce the loss caused by uncertain risk and the psychological gap caused by loss.

logistics distribution path; the prospect theory (PT); interval probability; parameter sensitivity

F252

A

1672 − 7029(2019)10− 2628 − 08

10.19713/j.cnki.43−1423/u.2019.10.032

2018−12−27

国家自然科学基金资助项目(71961016)；教育部人文社会科学研究规划基金资助项目(15XJAZH002，18YJAZH148)；甘肃省自然科学基金资助项目(18JR3RA125)；兰州交通大学“百名青年优秀人才培养计划”基金资助项目(兰交人发〔2017〕37号)

朱昌锋(1972−)，男，甘肃秦安人，教授，博士，从事轨道交通运输组织、物流管理研究；E−mail：cfzhu003@163.com

(编辑 蒋学东)