一种水下滑翔机盐度数据的噪声处理方法

易镇辉, 俞建成, 毛华斌, 张志旭, 练树民, 邱春华, 李先鹏*

一种水下滑翔机盐度数据的噪声处理方法

易镇辉1,3, 俞建成2, 毛华斌1, 张志旭1, 练树民1, 邱春华4, 李先鹏1*

(1. 中国科学院 南海海洋研究所 热带海洋环境国家重点实验室, 广东 广州, 510301; 2. 中国科学院 沈阳自动化研究所, 辽宁 沈阳, 110016; 3. 中国科学院大学 资源与环境学院, 北京, 100049; 4. 中山大学 海洋科学学院近岸海洋科学与技术中心, 广东 广州, 510275)

温盐深传感器(CTD)是水下滑翔机常规搭载的模块, 可以高效地观测海水的温度、盐度和压强。但在盐度的计算过程中, 热滞后误差问题普遍存在且不可忽略。对此, Morison 等提出能有效修正热滞后误差的方法。文中对2017年7~8月间, 8台“海翼”水下滑翔机搭载的滑翔机有效载荷CTD(GP-CTD)数据进行处理, 用中值滤波和移动平滑滤波解决盐度峰的问题, 基于上述方法, 对盐度数据进行热滞后修正, 发现热滞后误差与垂向温度结构和水平分辨率密切相关; 在剖面插值过程中, 由海洋内部波动引起的压强振荡影响插值结果, 会带来很大的盐度差和温度差, 并基于CTD剖面数据, 提出一种海洋内部波动的简单识别方法。文中的工作可为水下滑翔机的数据质量控制和海洋现象的捕捉提供参考。

水下滑翔机; 温盐深传感器; 热滞后修正; 剖面插值; 盐度

0 引言

水下滑翔机作为一种新型的无人水下航行器, 在海洋观测中起着非常重要的作用[1]。它通过改变自身重力与浮力的大小来控制垂向的滑行速度, 通过调整滑翔翼来实现水平运动, 从而在海水中以锯齿型轨迹航行。水下滑翔机具有制作成本低、能耗小、续航能力强、自主可控等优点, 还能进行模块化设计, 可以搭载不同的传感器, 对海洋进行大规模、长时间、全天候和高分辨率的自主实时观测, 弥补了传统海洋观测手段的缺陷, 具有广阔的应用前景[2]。

水下滑翔机的概念是1989年由Stommel[3]首次提出。1991年, 美国Teledyne Webb Rese- arch(TWR)公司研制了最早的水下滑翔机Slo- cum[4]; 1999年, 美国Scripps海洋研究所和Woods Hole海洋研究所共同研发了工作深度更大的Spray[5]; 随之, 美国华盛顿大学应用物理实验室开发了更高效节能的Seaglider[6]。这3类为第1代水下滑翔机, 在海洋观测中应用最为广泛。之后的产品朝着多样化发展, 如: 混合推进水下滑翔机(hybird-driven underwater glider, HUG)[7]、深海水下滑翔机[8]、飞翼水下滑翔机[9]和波浪滑翔机(wave glider, WG)[10]等相继研制。

相比国外, 国内对水下滑翔机的研究起步较晚, 但也取得了显著的进展。2005年, 天津大学研制的温差能驱动的水下滑翔机成功进行了水域测试[11]; 同时, 中国科学院沈阳自动化研究所研发的原理样机也在湖上进行评估测试[12-13]。随后, 多家科研单位或院校也进行了相关技术研发并取得了技术突破, 如中国海洋大学[14]、国家海洋技术中心[15]、中国船舶重工集团公司第710研究所[16]、第702研究所[17]、华中科技大学[18]、浙江大学[19]、大连海事大学[20]、上海交通大学[21]和西北工业大学[22]等, 特别是在混合推进水下滑翔机和深海水下滑翔机的研发方面, 国内发展已经与国际水平同步。

水下滑翔机可以搭载传感器对海水进行测量, 其中温盐深传感器(conductivity temperature depth, CTD)是其搭载的最常规和最重要的传感器, 可以测量海水的温度、电导率和压强, 进而推导出海水的盐度和密度等参数。但是对于传统CTD, 由于电导传感器的热惯性, 温度和电导率的测量会不同步, 电导传感器要消耗时间来适应周围海水, 例如: 从暖水到冷水过程中, 需要扩散储存的热量, 相比电导传感器, 温度传感器的反应速度较快。这种传感器反应时间的滞后导致了计算盐度时存在误差, 被称为热滞后效应[23]。

Lueck和Picklo[23-24]首次提出一种热滞后修正的数值算法, 并用SBE(Sea-Bird electronics Inc.)的电导元件进行验证, 该算法可以有效移除盐度偏差, 对其中参数的敏感度不高, 具有普适性。Morison等[25]提出了一种实用的确定热滞后修正振幅和时间常数的方法, 最小化下潜—上升过程的温盐曲线中2个盐度之间的差异, 并根据SBE-9 CTD数据所得到的经验结果, 得出和都是平均速度的函数。Johnson等[26]用3台锚定的SBE-41CP CTDs数据对电导元件的热惯性进行评估和修正, 并对装备了SBE-41 CTD的Argo浮标剖面进行筛选, 选取了上百个强温跃层之上充分混合的表层剖面进行热滞后修正。 Bishop[27]修正了Slocum 水下滑翔机数据的热滞后效应, 根据Lueck、Picklo和Morison 等的方法, 用Slocum 水下滑翔机的平均垂向速度来计算修正参数。Menash等[28]对SBE-4的数据进行热质量惯性修正, 以Morison等的方法为基础, 提出一种经验方法来确定修正参数的最优值, 并计算出在强温跃层中普遍适用的参数值。Garau 等以Morison 等的工作为基础, 提出了不带泵的Slocun CTD数据的热滞后修正方法, 该方法优点如下: 使用水下滑翔机自身的可变速度, 同时不需要参考剖面; 最小化2个CTD剖面(1个为下潜过程, 1个为上升过程)组成的T-S曲线围成的面积所确定的目标函数, 从而确定4个修正参数[29]。这种方法被用来进行常规水下滑翔机CTD的数据处理。Liu 等[30]对比了Morison 等的方法和Garau 等的方法在强温跃层的可行性和局限性, 并提出用中值滤波(=7)的方法移除较大的盐度峰, 可以明显改善热滞后修正的效果。Eric- ksen[31]对Seaglider上不带泵的电导元件进行了盐度估计。Frajka-Williams等[32]根据Ericksen 等的模型和Lueck的热滞后理论, 对Seaglider数据进行了简单的热惯性修正。

文中利用Morison 等的方法对2017年7～8月期间南海中尺度涡多滑翔机集群观测的几千个CTD剖面数据进行热滞后修正。Morison 等的方法能有效地修正带泵CTD的热滞后误差[25], 但是在层结强的深度上, 热滞后修正效果不好[28]。

文中将评估该方法在温跃层的修正效果, 讨论的问题有: 1) 提高盐度热滞后修正的效果; 2) 讨论盐度热滞后误差的影响因子; 3) 改善剖面插值效果。

1 “海翼”水下滑翔机数据热滞后修正方法

1.1 “海翼”水下滑翔机数据

2017年7~8月期间, 由中国科学院沈阳自动化研究所组织的南海中尺度涡多滑翔机集群观测, 以揭示南海北部涡旋的精确三维结构, 研究涡旋不对称性导致的南海北部跨陆坡物质能量输运, 文中研究的为其中的8台。该次为期1个月的观测获取了3075个CTD的剖面数据, 详细信息见表1。对原始数据进行预处理, 去掉原始数据中一些异常的采样过程和奇异值。异常的采样过程主要分为以下几种: 1) 只有下潜过程的数据; 2) 采样时间不连续, 文中定义为存在大于10 m压强差的采样过程; 3) 高频振荡; 4) 压强一直为0。8台水下滑翔机总共出现的异常采样过程分别有2、22、6和2次, 所以有效剖面数为3 043个。

表1 8台“海翼”水下滑翔机基本信息

“海翼”水下滑翔机搭载的CTD为Slocum 滑翔机有效载荷CTD(glider payload CTD, GP-CTD), 能测量电导率、温度和压强。在水下的滑翔轨迹呈锯齿形, CTD传感器整个过程都处于采样观测状态(见图1)。工作深度为300 m的水下滑翔机完成1个采样过程的时长是30~40 min, 出入水位置间的距离约为0.5 km; 工作深度为1 000 m的水下滑翔机完成1个采样过程的时长约3 h, 出入水位置间的距离约为2 km。8台水下滑翔机基本位于南海北部海盆的深水区, 其中4台水下滑翔机(300K001, 300K003, 1000J005和1000J008)为东北—西南走向的来回断面观测, 剩余4台基本为西北—东南走向的来回断面观测(见图2), 每台水下滑翔机每天滑翔的距离为25~30 km。

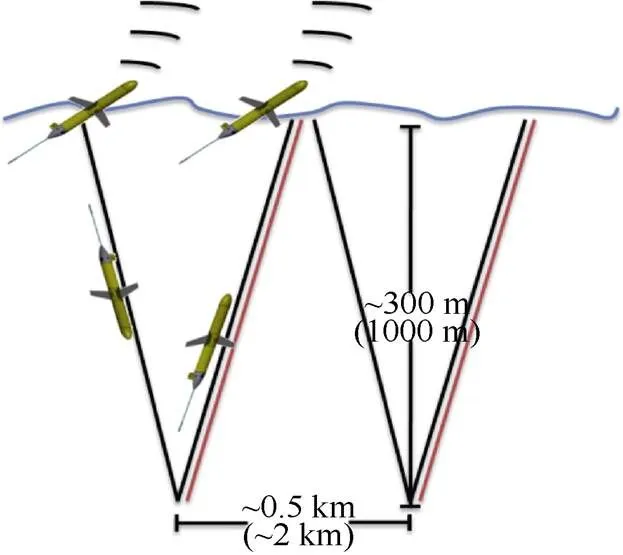
图1 “海翼”水下滑翔机滑行路径图

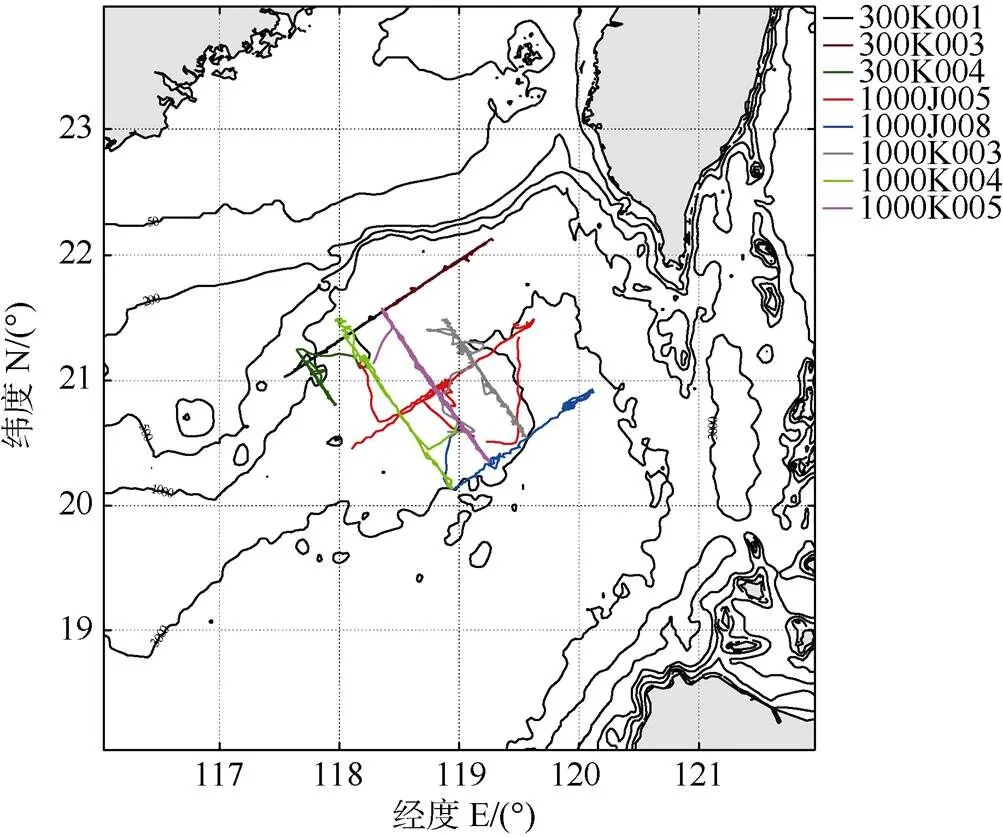
图2 8台水下滑翔机观测列阵位置图

1.2 热滞后修正方法

在盐度计算过程中, 由于温度传感器和电导率传感器的瞬间反应速度不同步而导致的误差不容忽视。1990年, Lueck[23]提出了热滞后修正的理论模型, 具体如下。

电导率修正值

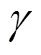
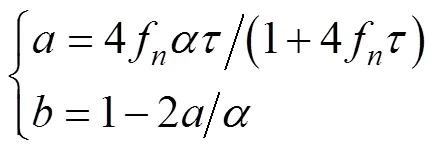
式中:f为折叠频率(Nyquist频率);和分别为误差的振幅和时间常数, 二者都取决于通过电导单元的流速。Lueck的理论由Morison等进一步验证, 并根据经验结果, 得到计算系数和的等式

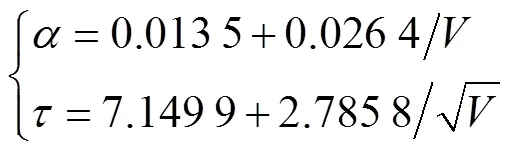
式中,为通过电导单元流速的平均速度。需要注意的是, Morison 等的研究是在传统CTD试验的基础上进行的, 流速已知, 假定为常数0.486 7 m/s, 所以系数和分别为0.0677和11.1431[25]。

Morison等在Lueck的理论基础上, 进一步提出通过估计电导单元的温度来实现温度和电导率的同步变化

式中, 温度修正值T加上测量的温度可得电导单元内的估计温度, 由此可依据测量的电导率来计算盐度。

相比而言, Morison等的方法因为不需提供电导率对温度的敏感度，而比Lueck的方法更为简单。

2 热滞后误差修正

在温跃层或盐跃层中, 盐度的垂向剖面会存在许多陡峭的峰[33], 这些峰不能被常规的平滑方法(如: 低通滤波)滤掉, 虽然插值过程也存在平滑的作用, 但未能将这种峰值去除[26], 所以就可能将这种峰值插值到标准的剖面上, 从而影响剖面整体结构和现象的判断, 特别是在尺度较小的过程中。

Emery等[34]提出可通过比较样本值的直方图检查离散值是否符合假定的概率分布函数, 以此来分离误差较大的点。另一种方法是对于所有的数据, 设定1个阈值(如±3, 其中,为标准差), 超过阈值则视为异常值。但是这些方法将异常值也当作样本的一部分, 从而影响概率分布函数和阈值的计算[34], 所以并不适合用来去除这些盐度峰值。Mensah等[28]提出用中值滤波有效去除CTD数据中温度、电导率和盐度中存在的峰值现象。Liu等[31]用窗口为7的中值滤波有效地去除盐度存在的峰值, 并且保证原有数据的变化趋势。窗口为的中值滤波可以表示为

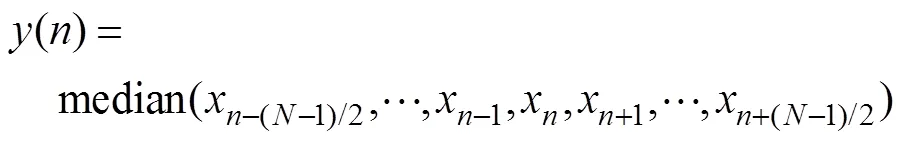
但从数据的处理结果发现, 窗口为7的中值滤波并不能将盐度的一些峰值完全滤掉(见图3(a)), 窗口宽度需要重新调整。

选取300K001水下滑翔机的第389个采样过程, 记为300K001-389(入水时间2017/7/26 13:20: 19, 入水位置(117.97ºE , 21.30ºN); 出水时间2017/7/26 14:03:22, 出水位置(117.80ºE , 21.30ºN))作为典型例子。由图3(a)可以看出, 中值滤波可以很好地移除陡峭的峰值(如92 m处), 对于较缓的峰值(如85 m处), 不同窗口宽度的中值滤波有不同的效果, 11点中值滤波基本能移除盐度峰值, 15点中值滤波则因窗口过大, 可能会改变盐度本身的变化趋势(如90 m处)。为了移除盐度峰值和保留盐度本身的变化趋势, 窗口为13的中值滤波将用于移除原始数据的盐度峰值, 对应的垂向深度为10 m左右。但是, 中值滤波存在弱化盐度变化的问题, 经过中值滤波处理后, 可能几个甚至十几个相邻数值相等, 对应的垂向深度为10 m的盐度值相同, 这显然不符合观测事实, 移动平滑滤波可以解决这个问题。窗口为的移动平滑滤波为

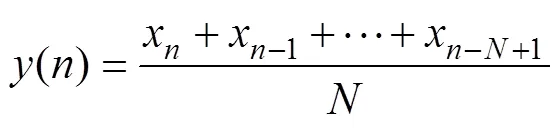
不同窗口的移动平滑滤波对盐度都有明显的平滑作用, 为了保守起见, 对中值滤波处理后的盐度进行窗口为7的移动平滑滤波(见图3(b))。

Morison等[25]提出的热滞后修正方法的基本假设是整个下潜—上升过程基本处于同一个水团, 海水的理化性质也基本不变, 所以在温度-盐度曲线(T-S曲线)上, 下潜剖面曲线与上升剖面曲线应相差不大。下潜和上升过程的盐度差可以表征该过程的盐度数据质量。中值滤波(=13)和移动平滑滤波(=7)处理后, 不管是原始盐度还是热滞后修正的盐度, 数据质量都有显著的提高, 下潜和上升过程向平均值聚拢, 更加符合同属一个水团的性质, 盐度差减小了0.1 psu左右(见图4), 这与热滞后修正属于同一个量级, 所以滤波移除盐度峰值同样重要。图中, 滤波处理包括中值滤波(=13)和移动平滑滤波(=7)。

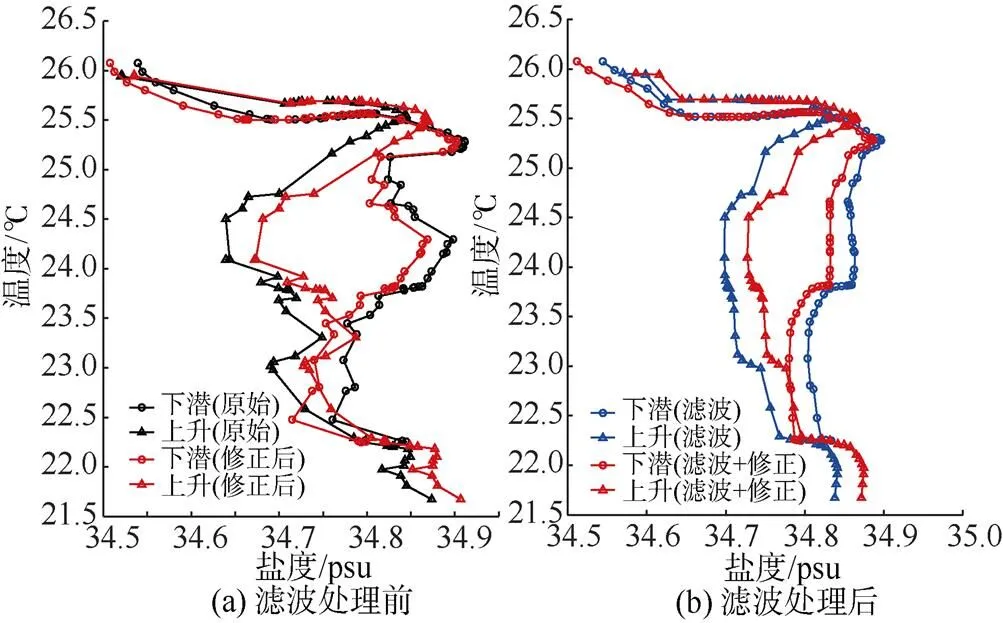
图4 滤波处理前后的温度-盐度曲线图

Morison 等提出的热滞后修正方法对原始的盐度有明显的修正(见图5), 特别是50~300 m的温跃层, 修正幅度平均值能达到0.02~0.05 psu, 最大值甚至超过0.1 psu, 特别是1000K003水下滑翔机, 修正幅度甚至能达到0.2 psu(见图5(f))。图中, 横坐标为热滞后修正盐度与原始盐度之差。相比原始数据, 下潜过程修正盐度值减小, 上升过程增加, 下潜—上升过程的差异进一步缩小, 使得修正后的盐度都向平均剖面聚拢, 这才是符合海水中的盐度分布, 在同一水团中, 海水的理化性质相似。300 m以深, 修正后下潜—上升过程的盐度基本一致, 修正效果明显优于温跃层, 这可能与海水的垂向温盐结构有关。但是, 在温跃层中, 热滞后修正下潜—上升过程的盐度仍然存在着差异, 甚至二者的变化趋势相反, 所以在温跃层中热滞后修正方法仍然需要改善。

3 热滞后误差的影响因子

盐度偏差(salinity error)的定义为热滞后修正下潜—上升过程之间存在的盐度差, 它是衡量热滞后误差的量, 盐度偏差越大, 说明热滞后现象越明显[28]。在观测期间, 海洋中存在许多波动现象, 可能会引起温跃层的起伏变化, 相应地, 在一次采样过程中, 下潜过程和上升过程的温盐结构存在着很大变化。为排除这种影响, 只选取下潜—上升过程温跃层深度之差都不超过2 m的剖面进行统计分析[28], 将温跃层上界设为温跃层深度, 温跃层上界的定义为温度超过海表面温度0.5℃所对应的深度[35], 海表面温度为5 m处的海水温度。8台水下滑翔机共选取了1 888个剖面进行讨论。

图5 8台水下滑翔机盐度差垂向分布图

3.1 垂向温度结构

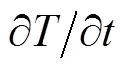
盐度偏差的垂向呈现双峰分布, 第1个峰值在50 m左右的深度上, 最大值能达到0.2 psu; 第2个峰值在200 m左右的深度上, 能达到0.05 psu, 只有第1个峰值的1/4 ; 400 m以深, 盐度偏差随深度变化很小并维持在0.01 psu以下(见图6(a))。温度梯度都为单峰变化, 梯度先增后减然后维持稳定, 最大值都在50 m左右, 约为0.11℃/db(见图6(b))。

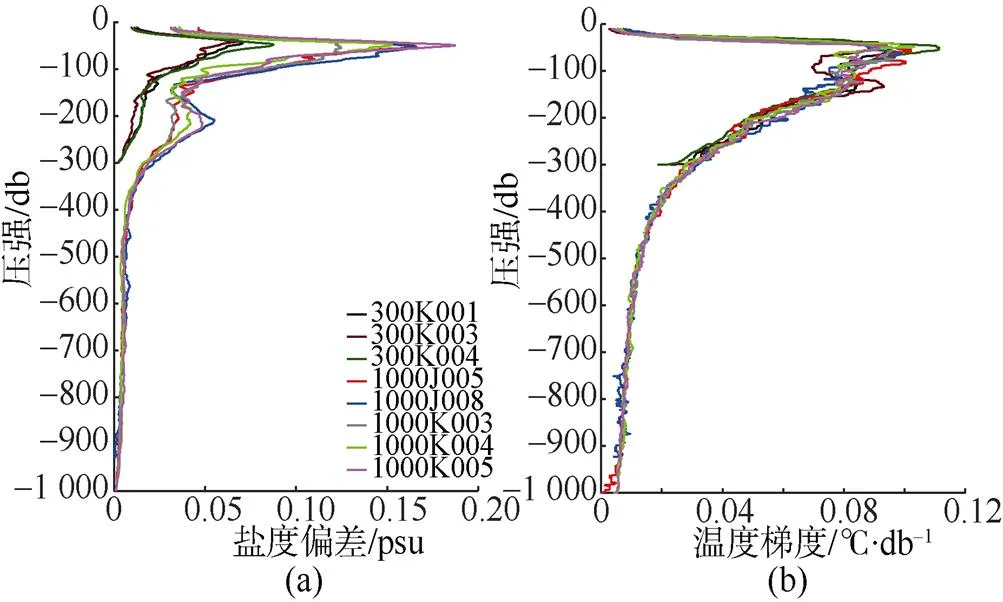
图6 8台水下滑翔机盐度偏差和温度梯度垂向分布图

选取温跃层以浅探讨盐度偏差随温度梯度的变化, 为了排除降水等因素对盐度的影响, 选取10~300 m作为研究深度。盐度偏差最大值所在深度为40~50 m, 在南海北部夏季, 可看成是混合层与温跃层的界限。在混合层, 盐度偏差与温度梯度呈现很好的线性关系, 其拟合优度为0.91~0.99, 温度梯度对盐度偏差的线性解释程度很高, 盐度偏差随温度梯度的增大而增大(见图7(a)); 在温跃层中, 盐度偏差与温度梯度线性关系很弱(见图7(b)), 图中颜色表示与图6相同。温度梯度相同时, 混合层的盐度偏差比温跃层的小, 这与混合层的剧烈混合有关。

图7 8台水下滑翔机盐度偏差随温度梯度的变化曲线

3.2 水平分辨率

水平分辨率的定义为出入水位置之间的距离, 该距离越大, 水平分辨率越小。由图6可知, 在温度梯度变化趋势基本一致的情况下, 300K001、300K003和300K004这3台水下滑翔机(下潜深度为300 m)的盐度偏差明显小于后面几台; 由图7(a)可知, 这3台的曲线也与其他几台存在明显分离, 盐度偏差相差约0.04 psu, 这与水平分辨率差异有关。当下潜深度为300 m 左右时, 水平分辨率约为0.5 km, 盐度偏差约为0.02 psu; 当下潜深度约为1 000 m时, 水平分辨率约为2 km, 相应的盐度偏差约为0.05～0.06 psu。随着水平分辨率的减小, 盐度偏差会增加, 但并非呈线性增加趋势(见表2)。这是因为水平分辨率减小, 下潜—上升过程的距离变大, 由于小尺度或次中尺度现象的影响, 水团性质发生改变, 盐度偏差变大。所以水平分辨率也是影响热滞后修正效果的因素, 随着水平分辨率增加, 热滞后修正效果变好, 热滞后误差减小, 下潜—上升过程就更加趋于一致。

表2 8台水下滑翔机平均水平分辨率和平均盐度偏差表

4 剖面插值和标准剖面选取

4.1 剖面插值

对8台水下滑翔机的盐度进行热滞后修正后, 下潜—上升过程盐度变得比较一致。为了对观测的断面进行更加直观的展现, 用一条标准的剖面来代表整个下潜—上升过程, 能准确反映整个过程的温盐变化。一维线性插值是1种简单有效的插值方法, 将下潜—上升过程的剖面一维线性插值到等米的标准剖面上, 然后对这2个剖面取平均值, 则该标准剖面代表整个下潜—上升过程。

在处理水下滑翔机温盐数据中发现, 下潜—上升过程中温盐分布存在异常起伏, 同一深度存在2个差异较大的观测值, 2次观测的海水分别属于不同水体, 对插值的结果势必造成影响。8台水下滑翔机存在这种现象的剖面有: 300K001- 490; 1000J008-56、62、72、75。选取剖面1000J008-56 (入水时间为2017/7/23 12:39:59, 入水位置为(119.27°E、20.30°N); 出水时间为2017/7/23 16:22:15, 出水位置为(119.24°E、20.33°N)评估该现象对插值结果的影响。为了对比水下滑翔机温盐异常起伏过程对插值结果的影响, 将该起伏过程移除, 然后进行一维线性插值, 前后进行对比, 为了清楚看出移除起伏过程前后的差别, 仅选取下潜过程250~450 m 进行具体分析。该起伏过程影响盐度的垂向分布, 存在1个盐度增长率相反的过程, 在同一深度上, 前一次测的是盐度高的水团, 后一次测的是盐度低的水团。插值后, 350 m处盐度突然降低, 形成1个盐度断层; 在350~380 m深度层, 移除起伏过程后的插值, 结果明显比移除前小并且光滑。移除起伏过程前后, 在同一深度上, 盐度相差最大能达到0.1 psu(见图8(a)和(d)), 与热滞后误差同一量级, 所以该起伏过程对插值结果带来的影响不可忽略。相同地, 温度在350 m处温度也突然降低, 形成1个温度断层, 而在350~ 380 m深度层, 温度移除起伏过程后的插值结果也明显比移除前小。移除起伏过程前后, 在同一深度上, 温度相差最大能达到2℃(见图8(c)和(f))。在T-S图上, 起伏过程移除前后在盐度为34.37~34.55 psu之间存在明显的差异, 而对应的深度为280~430 m (见图8(b)和(e))。该起伏过程还会给插值结果带来毛刺, 影响插值后温盐数据的质量。

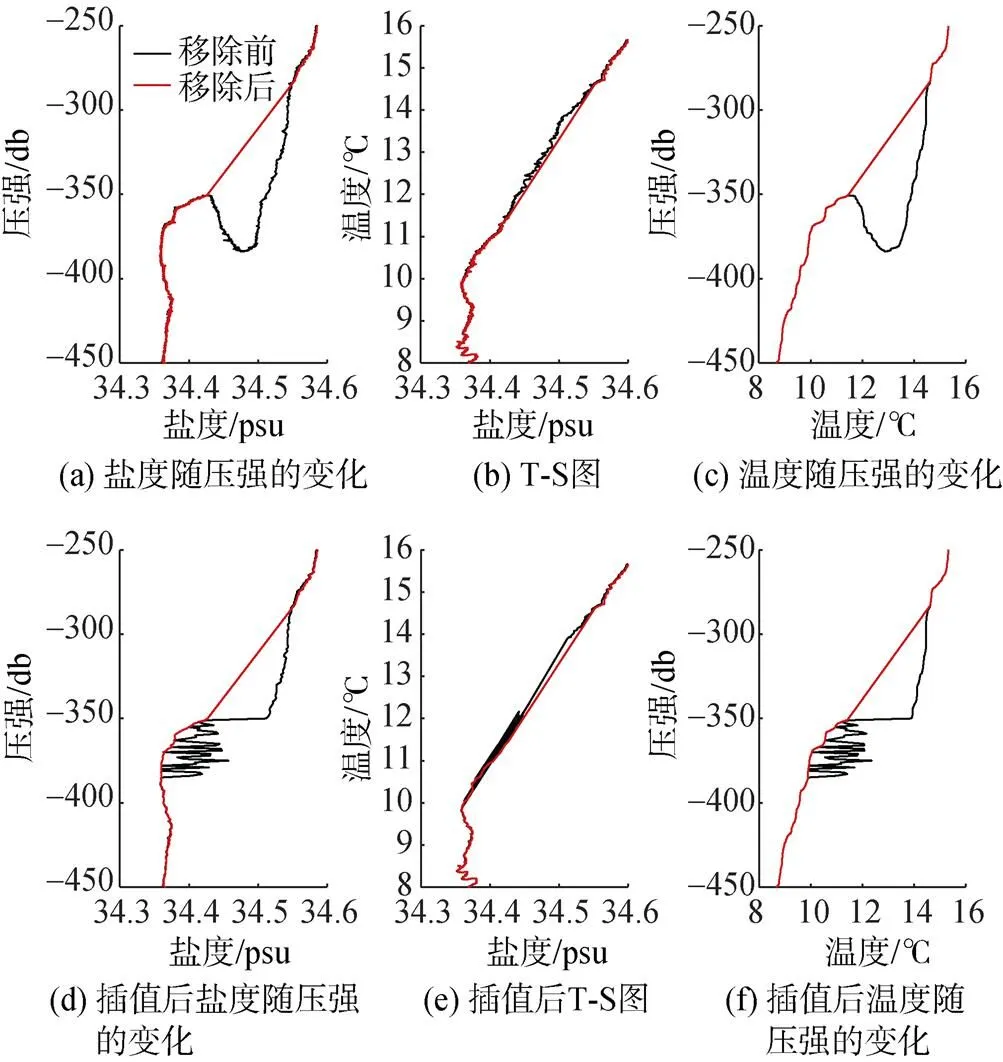
图8 1000J008-56下潜中温盐起伏过程对剖面插值的影响曲线

温盐起伏过程带来的盐度差和温度差对插值的影响不可忽略。在该过程中, 压强的变化不是单调的, 也存在着振幅为30 m左右的振荡过程(见图9), 与温盐起伏过程相对应, 所以温盐起伏过程是由压强的振荡引起的。压强振荡是因为受到海洋内部波动(如内波)的影响, 将正在下潜(或上升)的水下滑翔机抬升(或下落), 则同一深度存在着2个温盐观测值, 而2次观测的海水分别属于不同水体, 造成观测值相差较大。其他温盐异常起伏剖面都存在着压强振荡现象(见图10), 说明这种异常起伏并非传感器出错而导致的数据异常, 而是由海洋内部波动引起的。图10中, 红圈为海洋内部波动所在深度, 每个分图的剖面从左到右依次为300K001-490, 1000J008-56、62、72、75; 图中横坐标刻度为一条剖面的标度, 可以将这些剖面筛选出来, 这样不仅使插值结果更准确, 而且可以很好地研究海洋内部波动。

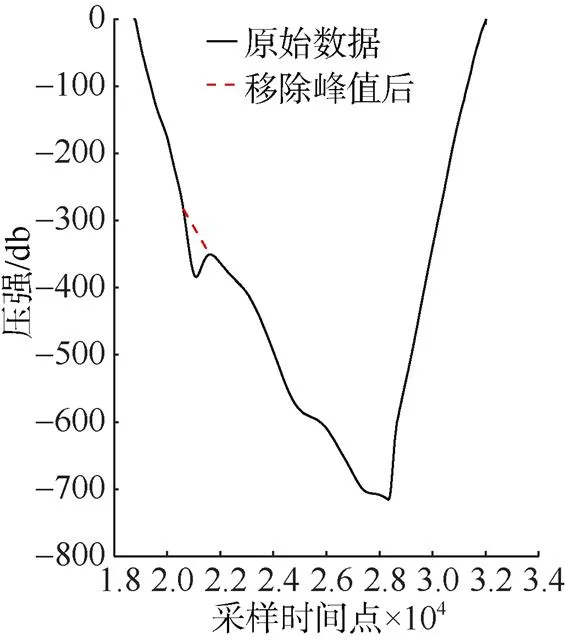
图9 1000J008-56 CTD剖面压强变化曲线

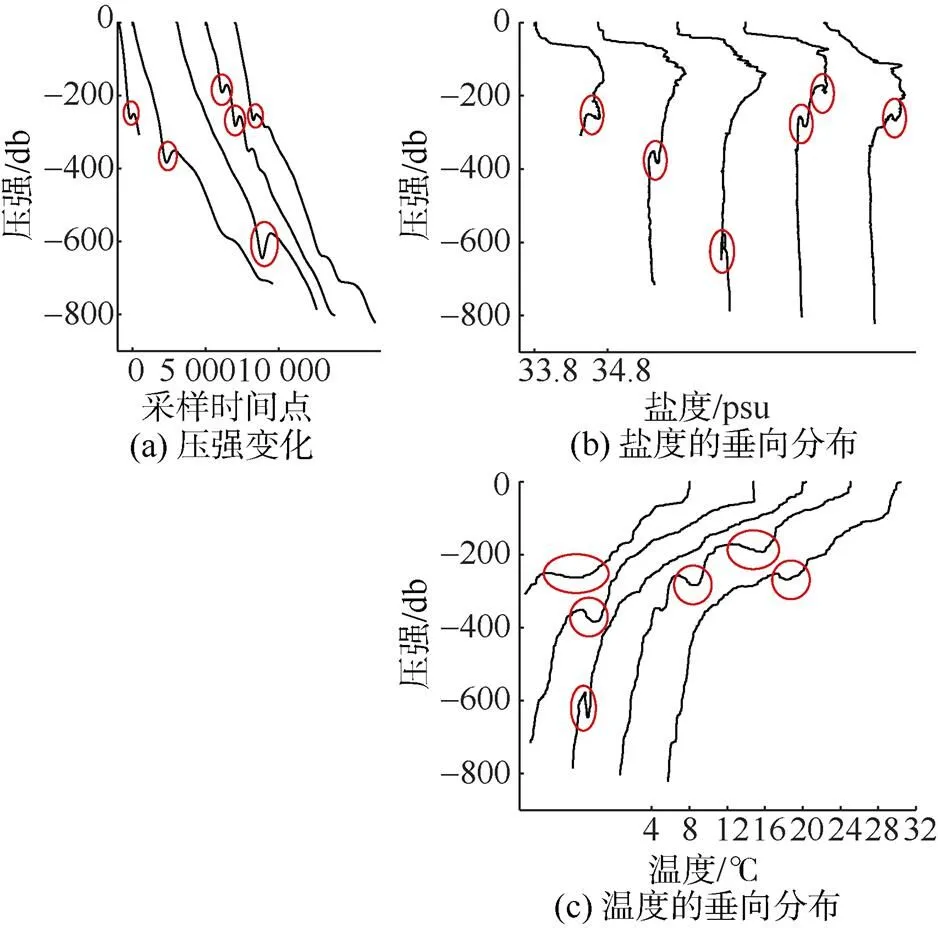
图10 不同剖面压强、盐度及温度变化趋势

相对应地, 海洋内部波动所在深度上的压强、盐度和温度也存在起伏过程, 其判定的标准为: 在下潜—上升过程, 同一深度(压强)存在着至少2个观测值(如: 温度和盐度等)(见图10)。由于海水盐度跨度小, 所以压强和盐度的起伏可以很好捕捉到海洋内部波动, 这种简单的识别方法可以有效地筛选出海洋内部波动, 为其研究提供宝贵的观测数据。

4.2 标准剖面选取

在选取标准的剖面来代表整个下潜—上升过程时, 常用的方法有3种: 1) 最普遍的方法是选择原始数据下潜过程为该标准剖面, 而将上升过程舍弃不用, 但往往会忽略很多尺度较小的现象(如空间尺度为-1 km 的次中尺度现象); 2) Liu Y等[31]提出, 将热滞后修正的下潜—上升过程的剖面, 一维线性插值到等米的标准剖面上, 然后对这3个剖面取平均, 用平均剖面代表整个下潜—上升过程, 由于热滞后修正需要迭代过程, 所以这种方法的计算量比较大; 3) 将原始数据的下潜—上升过程的剖面线性插值, 然后取平均剖面代表整个过程, 相对于方法2), 这种方法计算比较简单。与方法2)相比, 方法1)剖面盐度相差达0.5 psu, 其最值所在的深度集中在300 m以浅, 2种方法的盐度相差在50 m 左右达到最大(见图11中a1~a8)。图11中, 蓝色点为盐度差最小值, 红色点为盐度差最大值。而方法3)剖面与方法2)的盐度相差最大为0.05 psu, 最值对应深度也相对集中在300 m以上(见图11 中b1~b8)。南海北部温跃层所在深度为50~300 m, 在温跃层里, 2种方法与方法2）的盐度差都比其他深度大, 这是由于在温跃层明显的热滞后误差导致的。在文中试验中, 方法1)和方法3)所得剖面与方法2)的盐度差相差了一个量级, 0.5 psu的盐度差可能会引起盐度分布的显著变化, 从而改变水团的理化性质, 影响对海洋现象的捕捉和研究, 所以方法1)是不准确的; 对于方法3)的可行性, 可依据研究的问题而定, 对于大尺度现象, 可接受0.05 psu的盐度差, 但是对于小尺度现象, 0.05 psu的盐度差也可能影响盐度的分布, 所以该方法不适用。对于300 m以深的深海温盐梯度和热滞后误差都很小, 选取标准剖面时, 3种方法的差异不大。

5 结束语

文中用Morison 等的方法对8台水下滑翔机的CTD(带泵)数据进行热滞后修正, 讨论了热滞后误差的影响因子, 并探讨了海洋内部波动对温盐剖面插值的影响和标准剖面的选取, 得出以下结论。

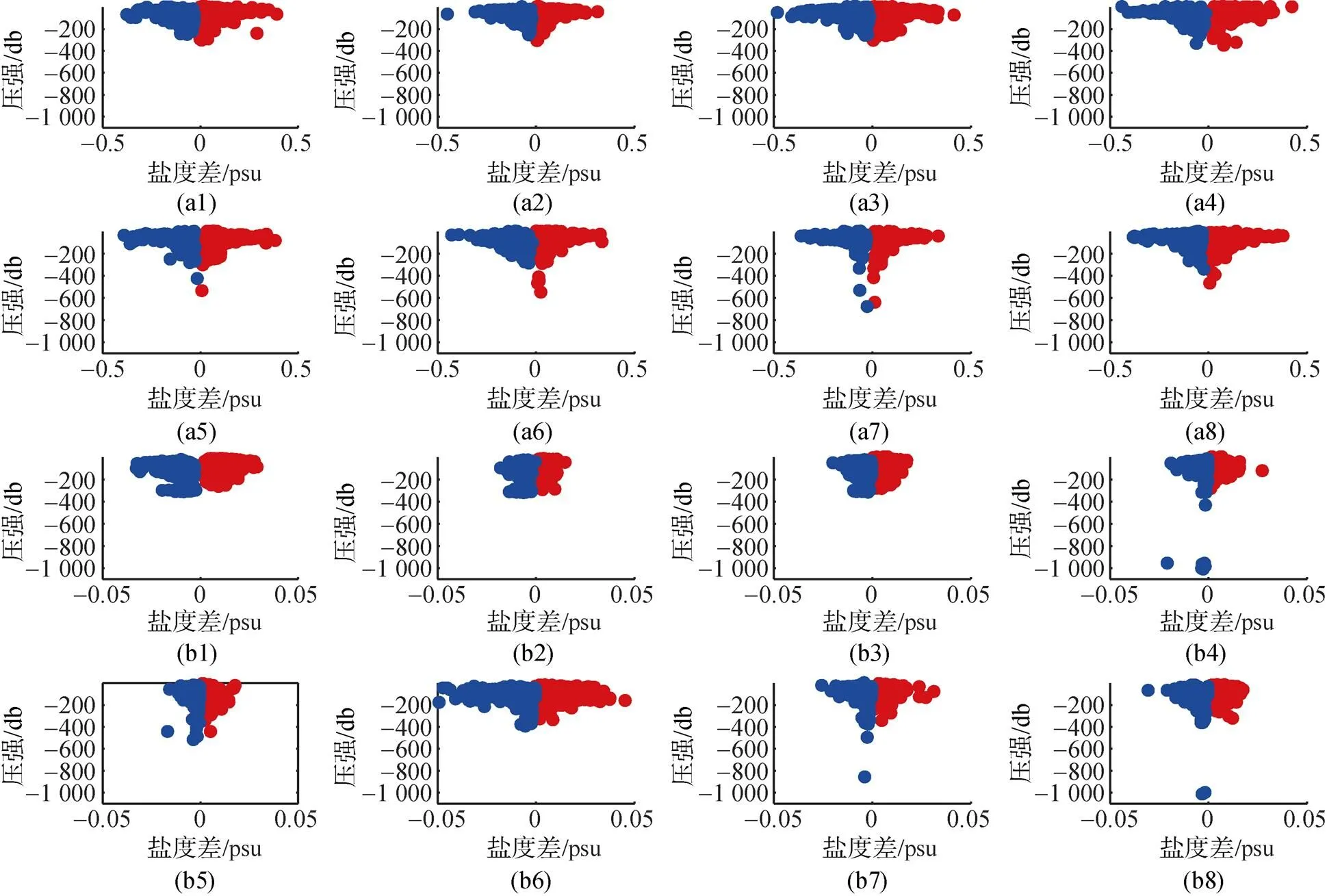
图11 8台水下滑翔机采用不同方法选取剖面与方法2)选取剖面的盐度差最值的垂向分布图

1) 用中值滤波(=13)和滑动平均滤波(=7)不仅能够移除盐度峰, 而且可有效解决中值滤波去趋势的问题, 提高热滞后修正效果。

2) 热滞后误差的影响因子包括: 垂向温度结构和水平分辨率。在混合层, 盐度偏差与温度梯度呈现很好的线性关系; 而在温跃层, 二者线性关系较差。水平分辨率减小, 盐度偏差则会增加, 但是并非呈线性增加趋势。

3) 在插值过程中, 海洋内部的波动(如内波)形成的压强起伏会引起温盐起伏现象, 带来很大的盐度差和温度差, 影响插值结果。同步的压强振荡和盐度起伏可以简单识别出海洋内部波动。

文中着重讨论CTD数据的处理, 尚未应用到海洋现象的探讨, 下一步工作重点是海洋中尺度涡和海洋内波的相关研究。

致谢: 感谢国家重点研发计划项目(2017YFC 0305904)对论文的支持和中国科学院沈阳自动化研究所提供的水下滑翔机数据。

[1] 沈新蕊, 王延辉, 杨绍琼, 等. 水下滑翔机技术发展现状与展望[J]. 水下无人系统学报, 2018, 26(2): 89-106.Shen Xin-rui, Wang Yan-hui, Yang Shao-qiong, et al. Development of Underwater Gliders: An Overview and Prospect[J]. Journal of Unmanned Undersea Systems, 2018, 26(2): 89-106.

[2] Rudnick D L, Davis R E, Eriksen C C, et al. Underwater Glider for Ocean Research[J]. Marine Technology Society Journal, 2004, 38(2): 73-84.

[3] Stommel H. The Slocum Mission[J]. Oceanography, 1989, 2(1): 22-25.

[4] Webb D C, Simonetti P J, Jones C P. SLOCUM: an Underwater Glider Propelled by Environmental Energy[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 447- 452.

[5] Sherman J, Davis R E, Owens W B, et al. The Autonomo- us Underwater Glider “Spray”[J]. IEEE Journal of Ocean- ic Engineering, 2001, 26(4): 437-446.

[6] Eriksen C C, Osse T J, Light R D, et al. Seaglider: a Long- range Autonomous Underwater Vehicle for Oceanographic Research[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 424-436.

[7] Bachmayer R, Leonard N E, Graver J, et al. Underwater Gliders: Recent Developments and Future Applications [C]//International Symposium on Underwater Technology. Taipei, China: IEEE, 2004: 195-200.

[8] Osse T J, Eriksen C C. The Deepglider: A Full Ocean De- pth Glider for Oceanographic Research[C]//OCEANS 2007. Vancouver: IEEE, 2007: 1-12.

[9] Wood S. Autonomous Underwater Gliders[J]. Underwater Vehicles, 2009, 26: 499-524.

[10] Hine R, Willcox S, Hine G, et al. The Wave Glider: A Wave-Powered Autonomous Marine Vehicle[C]//Oceans 2009, MTS/IEEE Biloxi-Marine Technology for Our Future:Global and Local Challenges. Biloxi: IEEE, 2009: 1-6.

[11] 武建国. 混合驱动水下滑翔器系统设计与性能分析[D]. 天津: 天津大学, 2010.

[12] 王树新, 李晓平, 王延辉, 等. 水下滑翔器的运动建模与分析[J]. 海洋技术学报, 2005, 24(1): 5-9.Wang Shu-xin, Li Xiao-ping, Wang Yan-hui, et al. Dyna- mic Modeling and Analysis of Underwater Gliders[J]. Oc- ean Technology, 2005, 24(1): 5-9.

[13] 王树新, 王延辉, 张大涛, 等. 温差能驱动的水下滑翔器设计与实验研究[J]. 海洋技术学报, 2006, 25(1): 1-5.Wang Shu-xin, Wang Yan-hui, Zhang Da-tao, et al. Design and Trial on an Underwater Glider Propelled by Thermal Engine[J]. Ocean Technology, 2006, 25(1): 1-5.

[14] Liu Y, Luan X, Song D, et al. Simulation for Path Plann- ing of OUC-II Glider with Intelligence Algorithm[C]// Intelligent Robotics and Applications: 10th International Conference, ICIRA 2017. Wuhan: Springer, 2017: 801- 812.

[15] 秦玉峰, 张选明, 孙秀军, 等. 混合驱动水下滑翔机高效推进螺旋桨设计[J]. 海洋技术学报, 2016, 35(3): 40- 45.Qin Yu-feng, Zhang Xuan-ming, Sun Xiu-jun, et al. Desi- gn of a High-Efficiency Propeller for Hybrid Drive Unde- rwater Gliders[J]. Journal of Ocean Technology, 2016, 35(3): 40-45.

[16] 陈刚, 张云海, 赵加鹏. 基于混合模型的水下滑翔机最佳升阻比特性[J]. 兵器装备工程学报, 2014, 35(2): 150- 152.Chen Gang, Zhang Yun-hai, Zhao Jia-peng, et al. Optim- um Lift-drag Ratio of the Underwater Glider Based on Mixture Models[J]. Journal of Sichuan Ordnance, 2014, 35(2): 150-152.

[17] 马冬梅, 马峥, 张华, 等. 水下滑翔机水动力性能分析及滑翔姿态优化研究[J]. 水动力学研究与进展, 2007, 22(6): 703-708.Ma Dong-mei, Ma Zheng, Zhang Hua, et al. Hydrodynamic Analysis and Optimization on the Gliding Attitude of the Underwater Glider[J]. Journal of Hydrodynamics, 2007, 22(6): 703-708.

[18] 李宝仁, 傅晓云, 杨钢, 等. 一种喷水推进型深海滑翔机: CN203581363U[P]. 2014-5-7.

[19] Yang C, Peng S, Fan S. Performance and Stability Analysis for ZJU Glider[J]. Marine Technology Society Journal, 2014, 48(3): 88-103.

[20] 杨豪, 陈济民, 初再宇. 圆碟形水下滑翔机的创新设计及应用前景[J]. 硅谷, 2015(4): 24-25.

[21] 倪园芳. 温差能驱动水下滑翔机性能的研究[D]. 上海: 上海交通大学, 2008.

[22] 田文龙, 宋保维, 刘郑国. 可控翼混合驱动水下滑翔机运动性能研究[J]. 西北工业大学学报, 2013, 31(1): 122- 128.Tian Wen-long, Song Bao-wei, Liu Zheng-guo. Motion Characteristic Analysis of a Hybrid-Driven Underwater Glider with Independently Controllable Wings[J]. Journal of Northwestern Polytechnical University, 2013, 31(1): 122-128.

[23] Lueck R G. Thermal Inertia of Conductivity Cells: Theory[J]. Journal of Atmospheric & Oceanic Technology, 1990, 7(5): 741-755.

[24] Lueck R G, Picklo J J. Thermal Inertia of Conductivity Cells: Observations with a Sea-Bird Cell[J]. Journal of Atmospheric & Oceanic Technology, 1990, 7(5): 756-768.

[25] Morison J, Andersen R, Larson N, et al. The Correction for Thermal-Lag Effects in Sea-Bird CTD Data[J]. Journal of Atmospheric & Oceanic Technology, 1994, 11(11): 1151-1164.

[26] Johnson G C, Toole J M, Larson N G. Sensor Corrections for Sea-Bird SBE-41CP and SBE-41 CTDs*[J]. Journal of Atmospheric and Oceanic Technology, 2007, 24(6): 1117- 1130.

[27] Bishop C M. Sensor Dynamics of Autonomous Underwater Gliders[D]. Newfoundland: Memorial University of Newfoundland, 2008.

[28] Mensah V, Le Menn M, Morel Y. Thermal Mass Correcti- on for the Evaluation of Salinity[J]. Journal of Atmosph- eric and Oceanic Technology, 2009, 26(3): 665-672.

[29] Garau B, Ruiz S, Zhang W G, et al. Thermal Lag Correction on Slocum CTD Glider Data[J]. Journal of Atmo- spheric and Oceanic Technology, 2011, 28(9): 1065-1071.

[30] Liu Y, Weisberg R H, Lembke C. Glider Salinity Correction for Unpumped CTD Sensors Across a Sharp Therm- ocline[J]. Coastal Ocean Observing Systems, 2015, 17: 305-325.

[31] Eriksen C C. Salinity Estimation Using an Unpumped Conductivity Cell on an Autonomous Underwater glider[C]//Fourth EGO Conf. Larnaca, Cyprus: EGO, 2009.

[32] Frajka-Williams E, Eriksen C C, Rhines P B, et al. Determining Vertical Water Velocities from Seaglider[J]. Jo- urnal of Atmospheric and Oceanic Technology, 2011, 28(12): 1641-1656.

[33] Bray N A. Salinity Calculation Techniques for Separately Digitized Fast Response and Platinum Resistance CTD Temperature Sensors[J]. Deep Sea Research Part a Oce- anographic Research Papers, 1987, 34(4): 627-632.

[34] Thomson R E, Emery W J. Data Analysis Methods in Physical Oceanography[M]. Newnes, Amsterdam, Oxford and Boston, 2014: 639-664.

[35] Sprintall J, Tomczak M. Evidence of the Barrier Layer in the Surface Layer of the Tropics[J]. Journal of Geophy- sical Research Oceans, 1992, 97(C5): 7305-7316.

A Noise Processing Method for Salinity Data Underwater Glider

YI Zhen-hui1,3, YU Jian-cheng2, MAO Hua-bin1, ZHANG Zhi-xü1, LIAN Shu-min1, QIU Chun-hua4, LI Xian-peng1*

(1. State Key Laboratory of Tropical Marine Environment, South China Sea Institute of Oceanology, Chinese Acaderny of Sciences, Guangzhou 510301, China; 2. Shen Yang Institute of Automation Chinese Academy of Sciences, Shenyang 110016, China; 3. College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China; 4. The Center for Coastal Ocean Science and Technology, School of Marine Sciences, Sun Yat-sen University, Guangzhou 510275, China)

Conductivity-temperature-depth(CTD) sensor on underwater glider is used to measure temperature, salinity and pressure of sea water. However, in the calculation of salinity, thermal lag error is a common problem but cannot be neglected. In this paper, eight glider payload CTD(GP-CTD) data of underwater gliders “Sea Wing” obtained during July – August, 2017 are processed. Median filter and sliding smoothing filter are used to solve the problem of salinity peak. The salinity data are corrected considering the thermal lag based on the thermal lag correction method proposed by Morison, et al. It is found that the vertical temperature structure and horizontal resolution are closely related to the thermal lag error. In the process of profile interpolation, the pressure oscillation caused by ocean internal fluctuation affects the interpolation results, resulting in significant error in temperature and salinity. Based on the CTD profile data, a simple identification method of ocean internal fluctuation is proposed. This study may provide reference for data quality control and marine phenomena capture of underwater gliders.

underwater glider; conductivity-temperature-depth(CTD); thermal lag correction; profile interpolation; salinity

TJ630; U674.941; P733.22

A

2096-3920(2019)05-0503-11

10.11993/j.issn.2096-3920.2019.05.005

易镇辉, 俞建成, 毛华斌, 等. 一种水下滑翔机盐度数据的噪声处理方法[J]. 水下无人系统学报, 2019, 27 (5): 503-513.

2018-11-30;

2018-12-27.

国家重点研发专项项目(2017YFC0305904).

*李先鹏(1983-), 男, 高级工程师, 主要研究方向为海上观测作业.

(责任编辑: 杨力军)