“海鲟4000”水下滑翔机水动力特性与滑翔性能研究

刘来连, 闵强利, 张光明

“海鲟4000”水下滑翔机水动力特性与滑翔性能研究

刘来连, 闵强利, 张光明

(中国船舶重工集团公司 第710研究所, 湖北 宜昌, 443003)

与一般水下滑翔机相比, 4 000 m水下滑翔机使用深度更深, 体型相对更大。为了克服海水密度变化的影响, 其浮力调节系统的体积调节量也更大。准确的动力学模型以及精确的水动力系数是实现其控制系统设计以及精确导航的基础。文中将在结构参数已定, 动力学模型已知的前提下获得精确的水动力系数, 对水下滑翔机性能进行预测, 并为控制系统提供控制变量和优化方向作为研究的重点。以“海鲟4 000”水下滑翔机为研究对象, 采用理论计算、计算流体动力学(CFD)仿真与试验数据分析相结合的方法, 分析了水平翼参数对其滑翔性能的影响; 获得了其在纵平面内做定常运动的水动力系数, 并对其性能进行预测; 通过试验数据分析, 获得典型滑翔状态下不同净浮力对应的滑翔速度, 并与理论计算进行对比分析, 验证理论计算的正确性。研究结果表明: 试验实际俯仰角控制与理论计算误差在5%以内; 试验实际净浮力下的滑翔速度与理论计算误差在15%以内, 满足控制系统相应控制量20%的误差需求。文中研究可为水下滑翔机控制系统的进一步优化和完善提供参考。

水下滑翔机; 滑翔性能; 水动力性能; 滑翔速度

0 引言

海洋是一座天然宝藏, 它既是人类实现可持续发展的重要物质来源, 又具有举足轻重的军事战略意义。在海洋开发的热潮及现代化战争呈现“信息化局部战争”态势下, 无人水下航行器(un- manned undersea vehicle, UUV)越来越被各国海军所重视。水下滑翔机就是近年来诞生的一种令人耳目一新的UUV, 其独特的设计显示出了极大的优势。它不需要任何燃料作为动力, 通过浮力调节装置实现自身浮力改变, 在净浮力、阻力及升力的作用下, 实现锯齿形滑翔观测运动。自1989年Stommel[1]提出水下滑翔机的概念之后, 水下滑翔机发展迅速, 较著名的有美国Webb研究所的slocum水下滑翔机[2]、华盛顿大学的Sea- glider水下滑翔机[3]和Scripps海洋研究所的spray水下滑翔机[4]。总体来说, 这些水下滑翔机的机体尺寸和质量相差不多(体长约2 m, 重约50 kg), 机身形状均为细长回转体, 这种设计尺寸小、阻力低, 同时保证了一定的装载量和续航力。

上述机构还对水下滑翔机运动及控制特性进行了研究, 并对其运动路径进行数值仿真, 验证了其运动及控制规律。然而这种仅仅依靠电池驱动的水下滑翔机需要获得长航程和高续航力, 除了需要配备高能电池外, 最重要的是要提高滑翔效率, 而升力和阻力是决定效率的关键因素。我国在水下滑翔机理论和技术方面, 天津大学、中国科学院沈阳自动化研究所、中船重工第710研究所、华中科技大学、浙江大学、中船重工第702研究所、中国海洋大学以及国家海洋技术中心等单位都相继开展了研究工作。其中: 天津大学研制的“海燕”混合驱动水下滑翔机综合了典型的水下滑翔机和传统自主水下航行器(autonomous un- derwater vehicle, AUV)的特点[5]; 中国科学院沈阳自动化研究所开展了“海翼”水下滑翔机研制, 用于深水海洋环境监测[6]; 浙江大学在水下滑翔机的运动稳定性和控制方面开展研究, 并开发了试验样机[7]。

文中以第710研究所“问海计划”项目中“海鲟4 000 ”水下滑翔机为研究对象, 采用理论计算、计算流体动力学(computational fluid dynamics, CFD)仿真与试验数据分析相结合的方法, 分析了水平翼参数对水下滑翔机滑翔性能的影响; 获得了其在纵平面内做定常运动的水动力系数, 并对水下滑翔机的性能进行预测; 通过试验数据分析, 获得典型滑翔状态下不同净浮力对应的滑翔速度, 并与理论计算进行对比分析, 验证了理论计算的正确性。

1 结构设计与水动力参数确定

1.1 “海鲟4000”水下滑翔机结构

“海鲟4000”水下滑翔机主要由滑翔机壳体、浮力调节装置、姿态调节装置及通信天线等组成,如图1所示。纵剖面的主要运动方式为滑翔运动, 与传统滑翔机的滑翔运动类似, 通过浮力调节装置和质心调节装置实现纵剖面锯齿形滑翔运动。

图1 “海鲟4000”水下滑翔机结构示意图

1.2 动力学模型

水下滑翔机的运动形式主要是在纵平面的“之”字形运动。因此, 首先需要建立其在纵平面内的动力学模型。

1) 坐标系建立

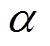
图2 “海鲟4000”水下滑翔机坐标系

2) 水动力模型

水下滑翔机在水下运动时, 会受到水动力的作用, 而水动力的大小直接决定着滑翔机的运动结果。水下滑翔机在纵平面运动时, 所受到的水动力主要有升力, 阻力和纵倾力矩。文献[9]研究表明, 小攻角情况下,和与攻角之间近似为线性关系、与攻角之间近似为二次函数关系, 并可表示为

1.3 水平翼参数特性分析

水下滑翔机的阻力主要由主体的湿表面积和外形决定, 升力由水平翼提供, 水平翼升阻比的计算公式为

由图3可知, 展弦比一定的情况下, 水平翼升阻比随攻角先急剧增加后逐渐减小, 且存在1个最大值; 随着后掠角增大, 最大升阻比保持不变, 其对应的攻角有所增大; 最大升阻比对应的攻角一般在6°~10°之间。

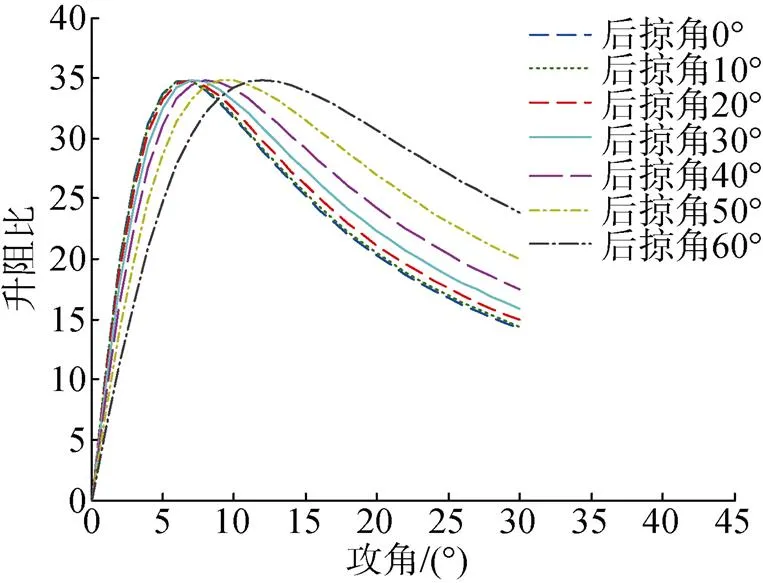
图3 水平翼升阻比随后掠角、攻角变化关系曲线

由图4可知, 后掠角一定, 水平翼升阻比随攻角先增后减, 同样存在1个最大值; 随着展弦比增大, 最大升阻比增大, 其对应的攻角有所增大; 最大升阻比对应的攻角一般在6°~10°之间。

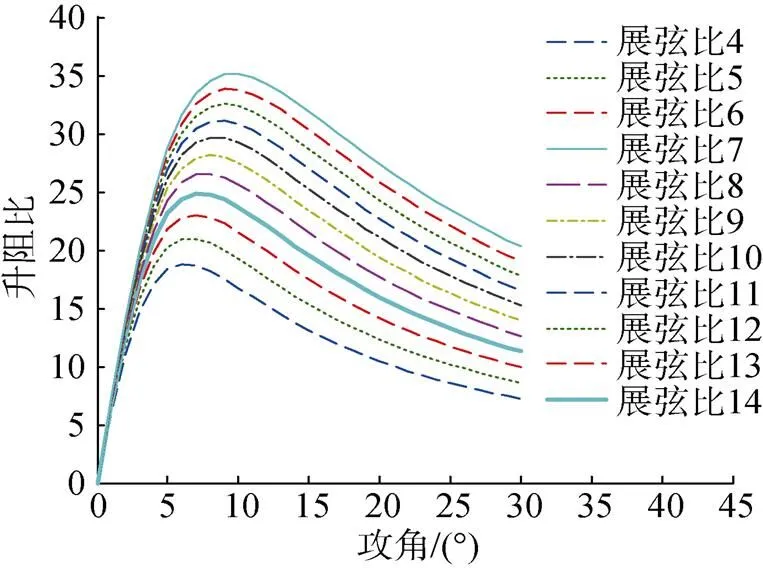
图4 水平翼升阻比随展弦比、攻角变化关系曲线

由于滑翔机正常滑翔状态下所对应的攻角为小攻角, 当攻角一定时(取小攻角), 升阻比随后掠角、展弦比的关系如图5所示。升阻比随后掠角的增加逐渐减小; 随着展弦比的增加, 升阻比增加, 但随着后掠角的增加, 减小的趋势更快。基本可以认为, 在小攻角情况下, 后掠角越小, 相应升阻比越大。

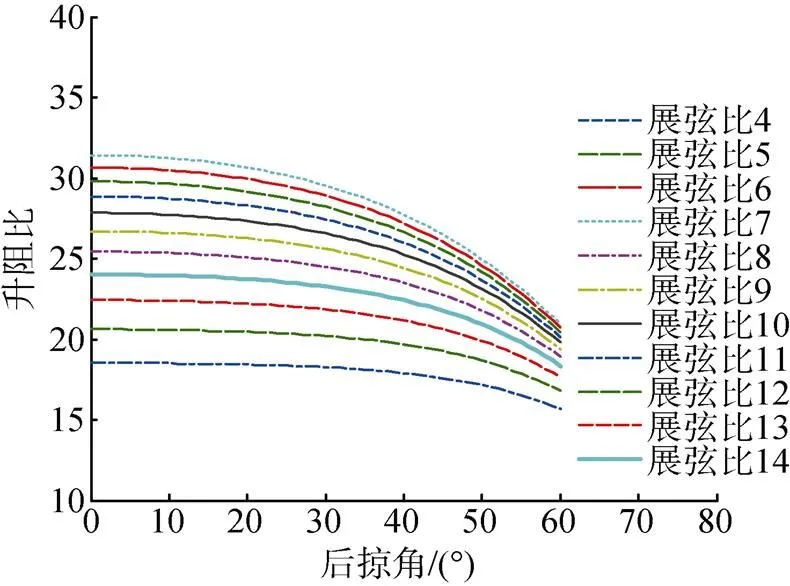
图5 水平翼升阻比随展弦比、后掠角变化关系曲线

根据上述计算分析, 可为“海鲟4000”水下滑翔机确定合适的展弦比和后掠角。

1.4 水动力参数确定

常用的水动力系数获取方法包括理论计算、试验和CFD方法。理论计算方法主要采用经验公式进行计算, 仅对于细长体外形及运动过程较为简单的模型有效[11]。试验方法主要包括风洞试验和拖曳试验等, 是目前比较常用且有效的手段, 但是试验成本高, 且耗时较长。CFD方法以计算机为硬件基础, 通过各类数学方法, 能够解决各种流体力学难题。

文中针对“海鲟4000”水下滑翔机, 采用CFD方法, 计算出了其水动力参数。计算状态见表1。

表1 水动力参数计算状态表

计算域为长度10、直径3.5的包围滑翔机的圆柱体(为滑翔机长度), 如图6所示。其旋转轴与滑翔机模型的对称轴重合, 进流边界面(入口)为圆柱体的前端面, 距模型首端的距离为4, 出流边界面(出口)为圆柱体的后端面, 距模型尾端的距离为5。整个计算域采用非结构化网格, 网格总数为120万, 网格质量0.3以上, 以保证求解精度。图7给出了计算结果示意图。

图6 计算域示意图

图7 水下滑翔机表面压力云图

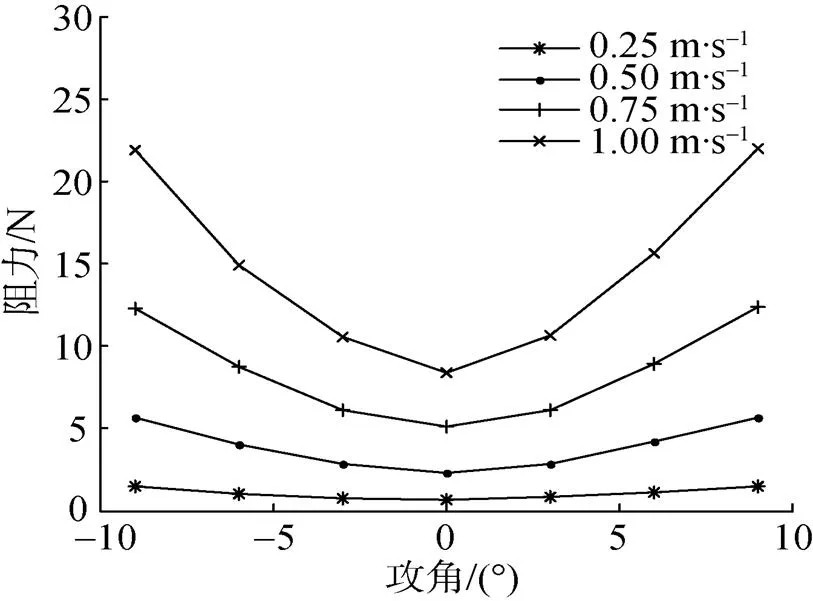
图8 不同速度和攻角下的阻力曲线

2 滑翔性能分析

根据以上水动力模型, 对“海鲟4000”水下滑翔机的滑翔运动进行受力分析, 得到以下平衡方程

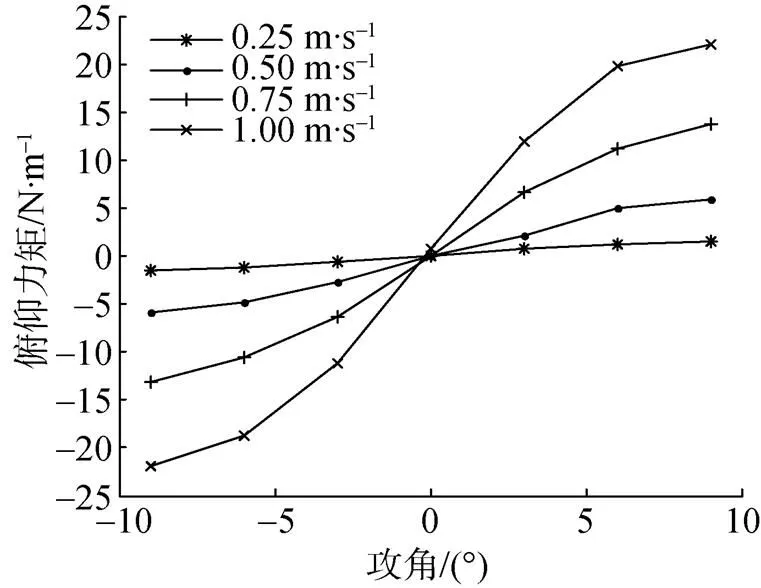
图10 不同速度和攻角下的俯仰力矩曲线

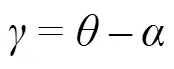
联合式(1)、式(2)和式(13)可得

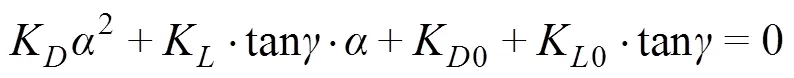
为使式(14)有解, 需满足

根据式(2)、式(10)和式(17), 可得速度与滑翔角的关系

图11给出了“海鲟4000”水下滑翔机在有效滑翔角范围内攻角与滑翔角的关系曲线。由图可知, 该滑翔机攻角范围为(0°~ 4.9°)＆(–4.4°~ 0°); 俯仰角范围为(12.6° ~ 90°)＆(–11.1° ~ –90°)。

图11 攻角与滑翔角关系曲线

图12给出了“海鲟4000”水下滑翔机在不同净浮力下水平速度与滑翔角的关系。从图中可以看出, 水平速度随着滑翔角的增加先增后减。在确定的净浮力下, 在有效滑翔角内存在1个最大水平速度, 该速度所对应的滑翔角约为36º, 对应的攻角为–1.45º, 俯仰角为34.55º。

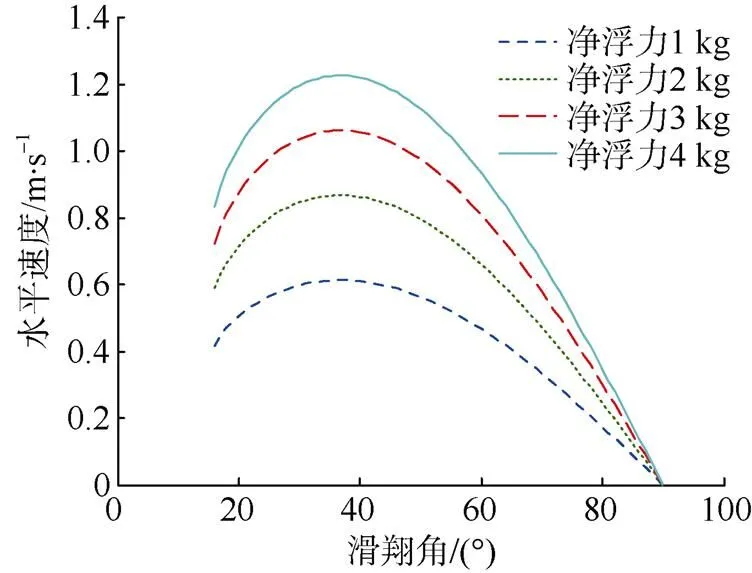
图12 水平速度与滑翔角、净浮力的关系曲线

图13~图16给出了“海鲟4000”水下滑翔机在典型滑翔角下, 滑翔速度、水平速度、垂直速度与净浮力的关系曲线。

图13 滑翔角为18º时速度与净浮力关系曲线

图14 滑翔角为27º时速度与净浮力关系曲线

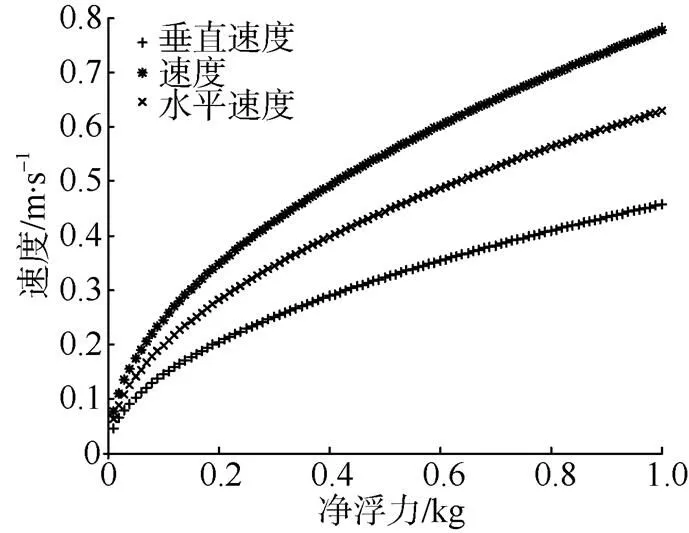
图15 滑翔角为36°时速度与净浮力关系曲线

由图可知, 净浮力增加可以同时增加滑翔的水平速度和垂直速度, 滑翔角超过36°以后, 水平速度将低于垂直速度。该计算结果即可与试验数据进行对比, 验证上述计算过程的正确性。

3 试验验证

2019年初对“海鲟4000”水下滑翔机进行了湖上试验(见图17), 获得了不同姿态下稳定滑翔的俯仰角度和滑翔速度数据。俯仰角度通过集成在滑翔机机体上的磁罗盘测量获得,滑翔速度通过机体上安装的压力传感器测量深度间接获得, 文中选取了2组典型滑翔角下有效试验数据曲线, 分别如图18~图20、图21~图23所示。需要说明的是, “海鲟4000”水下滑翔机控制程序中滑翔角是设定变量, 通过如图11所示的攻角与滑翔角的关系, 计算出对应的俯仰角, 从而对俯仰角进行控制。典型有效试验数据曲线如图18~图23所示。

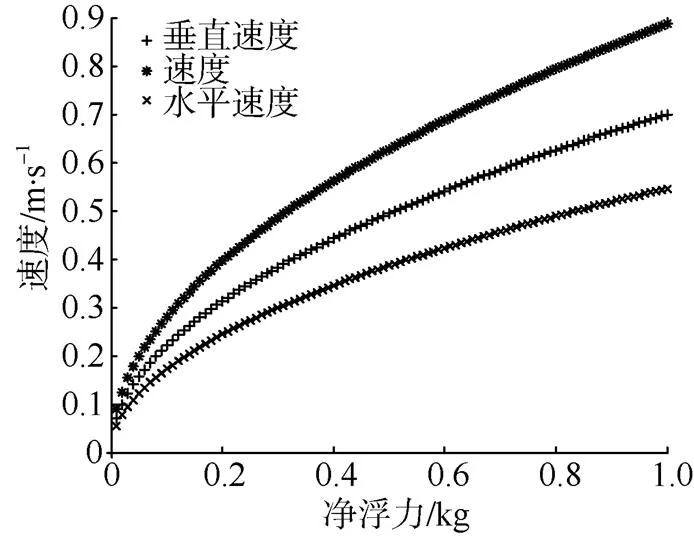
图16 滑翔角为52°时速度与净浮力关系曲线

图17 “海鲟4000”水下滑翔机湖上试验

图18 滑翔角为18°时深度变化曲线

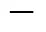
图19 滑翔角为18°时体积(净浮力)变化曲线

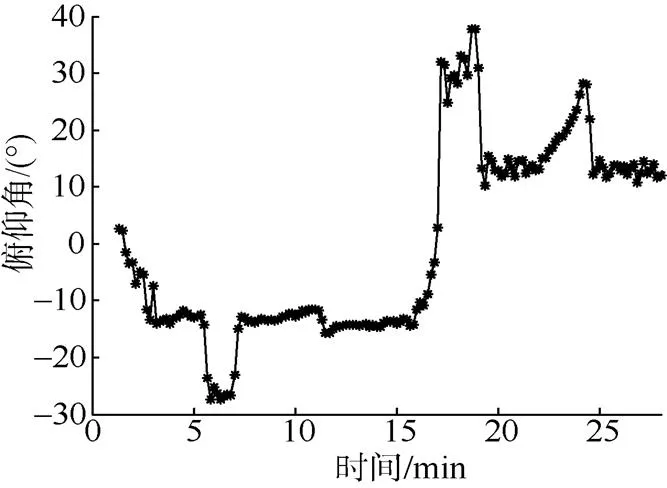
图20 滑翔角为18°时俯仰角变化曲线

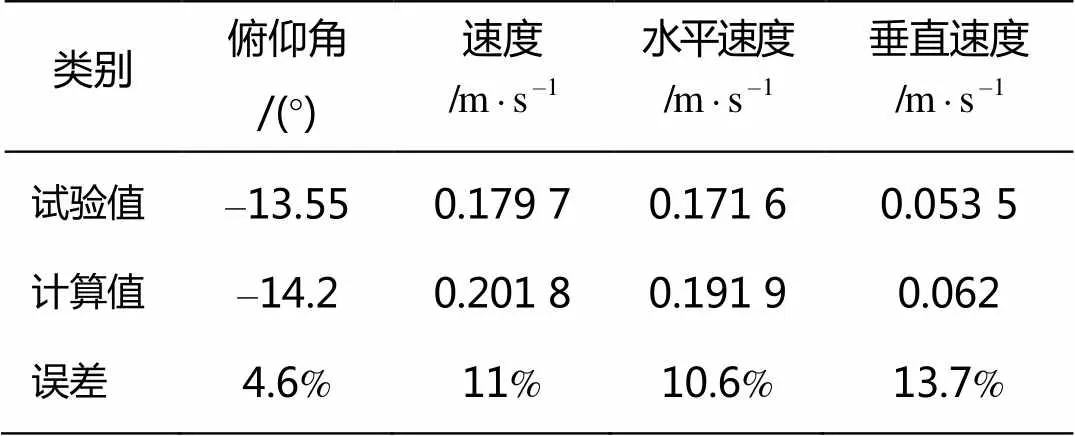
表2 滑翔角18°时滑翔数据表

从试验实测数据与分析计算的数据对比来看, 试验数据与分析计算数据基本吻合, 误差均在15%以内。存在误差的原因有: 1) 仿真计算模型过于理想, 与实际样机存在差异, 造成计算的水动力系数存在误差; 2) 实际样机浮力调节系统浮力调节量、俯仰角控制精度存在误差, 控制精度误差均为20%。因此, 从结果上看, 理论计算分析完全可以满足工程设计的需要, 并对工程设计具有很好的指导意义。

图21 滑翔角为27°时深度变化曲线

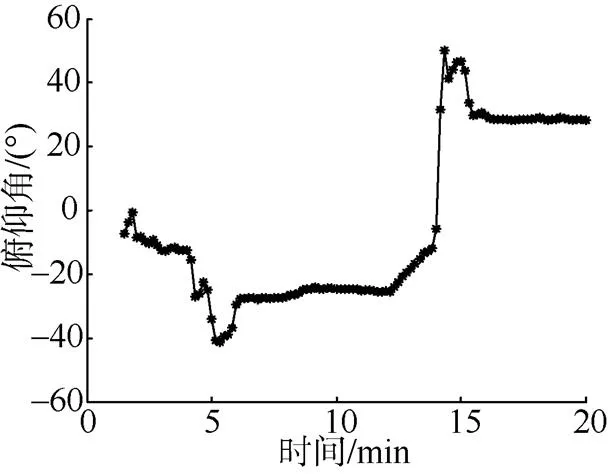
图23 滑翔角27°时俯仰角变化曲线

表3 滑翔角为27°时滑翔数据表

4 结束语

文中以“海鲟4 000 ”水下滑翔机为研究对象, 详细分析研究了其水动力特性和滑翔性能, 可得如下结论。

1) 参考相关文献对水平翼参数特性进行了分析研究, 获得了展弦比、后掠角、攻角与水平翼升阻比的关系, 最大升阻比对应的攻角一般为6°~10°, 可为工程设计提供参考。

2) 采用CFD方法计算出“海鲟4 000 ”水下滑翔机各个水动力参数, 并以此为基础, 详细分析研究了其滑翔性能, 获得其攻角范围为(0°~4.9°)＆(–4.4°~0°), 俯仰角范围为(12.6°~90°)＆(–11.1° ~ –90°), 其最佳抗流能力对应的滑翔角为36°。最后详细计算了其在不同典型滑翔角下, 滑翔速度、水平速度、垂直速度与净浮力的关系曲线, 对其滑翔控制具有很好的指导意义。

3) 对试验实测数据进行了分析研究, 获得了“海鲟4 000 ”水下滑翔机典型状态下的滑翔速度和俯仰角度数据, 并与分析计算数据进行了对比, 试验数据与分析计算数据基本吻合, 误差均在15%以内, 验证了分析计算过程的正确性, 满足控制系统相应控制量20%的误差需求, 并对控制系统的进一步优化和完善提供了依据。

文中的工作可对水下滑翔机的设计提供参考, 但其理论计算并未考虑海水密度变化及滑翔机受海水压力产生体积压缩量的影响, 也并未建立滑翔机改变航向的理论模型, 下一步将对此进行深入研究。

[1] Stommel H. The Slocum Mission[J]. Oceanography, 1989, 2(1): 22-25.

[2] Schofleld O, Kohut J, Aragon D, et a1．Slocum Gliders: Robust and Ready[J]. Journal of Field Robotics, 2010, 24(6): 473-485．

[3] Eriksen C C, Osse T J, Light R D, et al. Seaglider: A Long—Range Autonomous Underwater Vehicle for Oceano Graphic Research[J]．IEEE JournaI of Oceanic Engineering, 2001, 26(4): 424-436．

[4] Rudnick D L, Davis R E, Sherman J T. Spray Underwater Glider Operations[J]．Journal of Atmospheric and Oceanic Technology, 2016, 33(6): 1113-1122．

[5] Liu F, Wang Y H, Wang S X. Development of the Hybrid Underwater Glider PetreI-II[J]. Sea Technology, 2014, 55(4): 51-54

[6] Yu J C, Zhang A Q, Jin W M, et al. Development and Experiments of the Sea-wing Underwater Glider[J]. China Ocean Engineering, 2011, 25(4): 721-736.

[7] Fan S S, Woolsey C. Elements of Underwater Glider Performance and Stability[J]. Marine Technology Society Journal, 2013, 47(3): 81-98.

[8] Bhatta P．Nonlinear Stability and Control of Gliding Vehicles[J]．Recent Developments In Ruminant Nutrition, 2006, 4(10): 325-352．

[9] Leonard N E, Graver J G. Model-based Feedback Control of Autonomous Underwater Gliders[J]. Oceanic Engine- ering, 2001, 26(4): 633-645.

[10] Breshears D D, Whicker J J, Johansen M P, et a1．Wind and Water Erosion and Transport in Semi-aridshrubland, Grassland and Forest Ecosystems: Quantifing Dominance of Horizontal Wind-driven Transport[J]．Earth Surface Pr- ocesses and Landforms, 2003, 28(11): 1189-1209．

[11] Hess J L．Calculation of Potential Flow about Arbitrary Three-dimensional Lifting Bodies[M]. LongBeach: Doug- las Aircraft Company, 1969．

Research on Hydrodynamic Characteristics and Gliding Performance of Underwater Glider “HaiXun 4000”

LIU Lai-lian, MIN Qiang-li, ZHAN Guang-ming

(The 710 Research Institute, China Shipbuilding Industry Corporation, Yichang 443003, China)

Compared with common underwater glider, the 4 000-meter underwater glider needs larger volume adjustment of its buoyancy control system in order to overcome the influence of seawater density change. Accurate dynamic model and hydrodynamic coefficient are the basis for realizing its control system design and accurate navigation. On the premise that its structural parameters are determined and the dynamic model is known, this paper aims to obtain accurate hydrodynamic coefficient and predict its performance, so as to provide control variables and optimization directions for the control system. Taking the 4 000-meter underwater glider “HaiXun 4000” as the research object, theoretical calculation, CFD simulation and experimental data analysis are combined to analyze the influence of the horizontal wing parameters on the gliding performance of the underwater glider, hence the hydrodynamic coefficient of constant motion in longitudinal plane is obtained, and the performance of the glider is predicted. Through the analysis of test data, the gliding speeds corresponding to different net buoyancy under typical gliding conditions are obtained and compared with the theoretical calculation to verify the correctness of the theoretical calculation. The results show that the error between actual pitch angle control and theoretical calculation is less than 5%, and the error between gliding speed and theoretical calculation under the actual net buoyancy of the test is within 15%, meeting the error requirements of 20% of the corresponding control amount for the control system. This research may provide a reference for further optimization and improvement of the control system.

underwater glider; gliding performance; hydrodynamic characteristic; gliding speed

TJ630; U674.941; O352

A

2096-3920(2019)05-0488-08

10.11993/j.issn.2096-3920.2019.05.003

刘来连, 闵强利, 张光明. “海鲟4000”水下滑翔机水动力特性与滑翔性能研究[J]. 水下无人系统学报, 2019, 27(5): 488-495.

2019-07-09;

2019-08-20.

青岛海洋科学与技术国家实验室“问海计划”项目资助(2017WHZZB0101).

刘来连(1978-), 男, 高级工程师, 主要研究方向为水下机器人控制技术.

(责任编辑: 杨力军)