含水砂岩三轴蠕变力学特性试验研究

(内蒙古科技大学 土木工程学院，内蒙古 包头 014010)

1 研究背景

岩石流变力学是巷道支护设计工作的重要理论基础，也是岩石力学研究核心内容之一[1-2]。巷道顶底板中的岩体在未受到开采扰动及破坏之前均处于三向应力状态下，因此研究三向应力状态下岩石的变形和强度特性，对于探明岩石破坏机理、巷道各种动力灾害的成因均有着重要的工程实践意义[3]。本文研究对象为某浅埋巷道，其顶板在富水条件下蠕变变形显著，最终导致冒顶。故深入研究顶板砂岩在三轴条件下受水岩作用影响的蠕变力学特性很有必要。

目前关于水对岩石蠕变特性影响的研究已取得不少成果，巨能攀等[4]开展不同含水率下的泥岩三轴压缩蠕变试验，对泥岩蠕变的非线性特征进行深入研究，通过量化比较得出泥岩的非线性蠕变程度随含水率提升而愈发显著。刘秀敏等[5]以石膏岩为研究对象，进行天然与饱水状态下的三轴压缩蠕变试验，分析得出饱水试样的总蠕变量是天然试样的 3～5倍，等速蠕变量是天然试样的2～5倍，衰减蠕变量是天然试样的 4～7倍。李男等[6]以干燥和饱水状态下的砂岩为研究对象，开展剪切蠕变试验，研究发现水促进砂岩的蠕变应变及速率的增长，使蠕变破坏强度明显降低。李高阳[7]进行不同浸润条件下的煤岩单轴压缩蠕变试验，研究表明随着浸润时间的增加，煤岩的蠕变峰值应力逐渐降低，轴向应变呈现增大的趋势。

砂岩对水的作用十分敏感，在水环境中蠕变现象较为显著。鉴于此，本文以某浅埋巷道顶板含水砂岩为研究对象，开展不同饱水时间下的三轴压缩蠕变试验，从应变特征、蠕变速率和长期强度3个方面分析砂岩在水作用下的蠕变特性，并对其微观影响机制进行一定的分析。

2 砂岩基本力学特性及试验设计

2.1 试样制备及基本力学参数

试样取自某浅埋富水巷道顶板，密封后运回实验室加工成Φ50 mm×100 mm的圆柱样。经薄片鉴定，所取砂岩由碎屑物和胶结物组成，其中碎屑物占据绝对优势，约占总体的86%，其主要成分为石英(72%)、长石(10%)、岩屑(3%)、微量矿物(1%)等。胶结物约占总体的14%，其主要成分为方解石(13%)、绿泥石(1%)等。所取岩样天然状态下的基本物理力学参数如表1所示。

表1 岩样基本物理力学参数Table 1 Basic mechanical parameters of rock samples

2.2 试验设计

试验仪器采用YSJ-01-00岩石三轴流变试验机(见图1)，岩样饱水时间设置为0 (天然状态，含水率ω=1.96%)、1 (ω=3.64%),5 d(ω=5.78%)。将岩样置于水箱中进行自由饱水，每隔24 h称重一次并记录。依据砂岩埋深，将试验围压设置为2 MPa。为了合理设计蠕变试验的加载参数，首先对砂岩进行围压2 MPa下的常规三轴压缩试验，为了减小试验误差，蠕变试验和三轴压缩试验在同一台仪器上完成，图2为常规三轴压缩应力-应变曲线。

图1 试验仪器Fig.1 Test instrument

图2 应力-应变曲线Fig.2 Stress-strain curves

蠕变试验每级轴向荷载增量Δq=Kqf/n(其中K为材料的强度降低系数；qf为破坏偏应力；n为加载级数)。试验过程以0.5 MPa/s的速率施加围压，直至加到2 MPa，围压加载仅需4 s完成，较大程度避免仅有围压而无轴向荷载时位移采集系统可能产生的误差，待围压稳定后以0.1 mm/s的轴向位移速率施加轴向荷载，直到岩样破坏，蠕变试验共历时873 h。

图3 分级加载蠕变曲线Fig.3 Creep curves of staged loading

3 试验结果及分析

3.1 蠕变试验结果

图3为试验所得分级加载蠕变曲线。以图3(a)第2级加载为例，将其局部放大(见图4)，进行详细分析。利用Boltzmann线性叠加原理处理图3后得到分别加载蠕变曲线(见图5)。

图4 局部放大曲线Fig.4 Local magnification curve

图5 分别加载蠕变曲线Fig.5 Separate creep curves under staged loading

从图3—图5可知，试样在轴向荷载作用下，首先产生瞬时应变ε1，其次是蠕变变形ε2。蠕变变形分为3个阶段：衰减蠕变阶段、稳定蠕变阶段和加速蠕变阶段。在图4中，岩样在第2级应力水平下首先产生瞬时变形，瞬时应变ε1=0.275%，然后进入衰减蠕变阶段，衰减蠕变阶段应变率逐渐减小，历经0.51 h进入稳定蠕变阶段，在该阶段应变和应变率逐渐趋于稳定，此时蠕变量ε2=0.138%。岩样在最后一级应力水平下进入加速蠕变阶段，该阶段蠕变量和蠕变速率大幅度增大，最后岩样迅速破裂[8-9]。

表2 不同含水条件下的应变量对比Table 2 Comparison of strain under different water content conditions

3.2 蠕变试验结果分析

3.2.1 应变特征

砂岩在各级偏应力作用的瞬间，产生了轴向瞬时弹性应变，反映了砂岩具有弹性变形的特性。图6为不同饱水条件下瞬时应变、蠕变量随应力水平的变化曲线，由于饱水5 d的砂岩岩样在第4级加载时破坏，所以这里只取前4级的瞬时应变、蠕变量进行对比。表2为蠕变量与瞬时应变对比结果。

图6 不同饱水条件下的瞬时应变和蠕变量对比曲线Fig.6 Curves of instantaneous stress and creep with different moisture content

由图6(a)可看出，瞬时应变随应力水平增加呈线性增大趋势，天然状态下的线性增长趋势小于饱水后。在同一应力水平下，瞬时应变随着含水状态的增强而递增。杨彩红等[10]认为岩石抵抗瞬时弹性变形能力的大小由瞬时弹性模量来反映，瞬时应变越大，瞬时弹性模量越小。分析其原因可能为：在饱水条件下，岩石微裂纹不断扩展，孔隙更容易也更快地发生瞬时变形；同时水对岩石的物理、化学作用改变了岩石自身的成分和结构，使得瞬时弹性模量随饱水时间的增加而递减。

由图6(b)可看出，蠕变量随应力水平增加呈增大趋势，天然状态下的增长趋势小于饱水后，天然状态和饱水1 d呈线性增长趋势，饱水5 d呈非线性急剧增长趋势。这是由于饱水5 d时岩样在第4级加载便进入加速蠕变阶段，所以此时蠕变量剧增。在同一应力水平下，蠕变量随着含水状态的增强而递增。由此说明水的作用促进了岩石时效变形，使其流变特性更加显著。分析其原因可能为：天然状态下，砂岩总体上微裂隙不发育，颗粒间的联结较为紧密，随着蠕变的发展，颗粒间联结的能量不断积蓄，当达到一个临界值时，便发生破坏。饱水逐渐增加砂岩的含水率，颗粒在水的润滑作用下产生错动滑移[6]，颗粒间联结的能量更难积蓄，这个临界值更难达到，很可能也会降低，最终蠕变的发展相比天然状态会有一个更“艰巨”的过程，蠕变量也会随之增大。

由表2可看出，蠕变量与瞬时应变的比值范围维持在0.498～0.655之间，天然状态、饱水1 d和饱水5 d的平均比值分别为0.521，0.535，0.586，随着含水状态的增强而呈递增趋势。由此可知，随着含水状态的增强，蠕变量的增长幅度快于瞬时应变，含水状态的增强使得岩石的蠕变特性更加显著。

3.2.2 蠕变速率

蠕变速率求取方法参考张春阳等[11]的研究成果，选取 Δti时间内n个蠕变数据，求第n个数据与第n-1个数据之差(n>1)，并求各差值之和，即为Δti时间内的总蠕变增量，最后除以总时间Δti，得第i段时间内应变速率vi，计算过程如下。

(1)

图7为饱水5 d的蠕变速率曲线，限于篇幅，不再列出天然状态和饱水1 d的蠕变速率曲线。

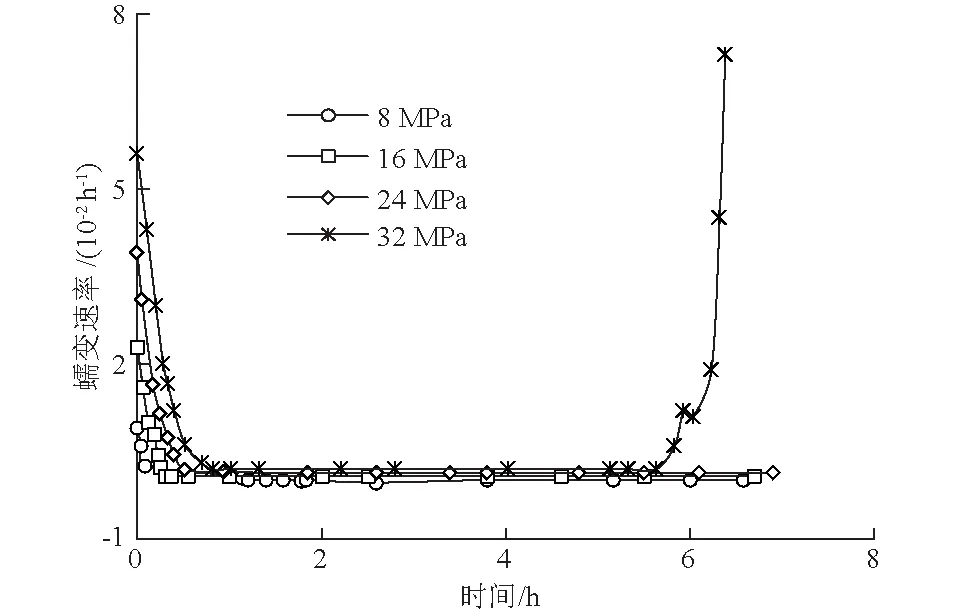
图7 不同加载下的蠕变速率曲线Fig.7 Curves of creep rate under different loading

由图7可看出，第4级加载曲线呈“桶”形，左侧、中间和右侧上升曲线分别代表衰减、稳定和加速蠕变阶段。从曲线外侧到曲线内侧，应力水平不断增大，初始蠕变速率和稳态蠕变速率逐渐增大。为比较不同饱水条件下的蠕变速率，取第4级加载进行对比，如图8所示。

图8 不同饱水条件下的蠕变速率曲线Fig.8 Curves of creep rate with different moisture content

由图8可知，随着含水状态的增强，初始、稳态蠕变速率都逐渐增大。天然状态、饱水1 d和饱水5 d的初始蠕变速率分别为1.69×10-2，3.87×10-2，5.54×10-2h-1，稳态蠕变速率分别为0.06×10-2，0.09×10-2，0.21×10-2h-1。从图8看，不同饱水条件下的蠕变速率差别并不大，实际上砂岩在水岩作用下，蠕变速率的变化很明显，可达数十倍增长。

3.2.3 长期强度

岩石蠕变长期强度主要用于在长时间作用下岩石强度损失程度的评价，长期强度是绝大多数岩土工程所必须引起重视的力学特性[12-13]。李良权等[12]、沈明荣等[13]和张强勇等[14]对岩石长期强度的确定方法进行了深入研究。目前较认可的确定方法主要有：①等时应力-应变曲线簇法；②稳态蠕变速率与应力水平关系曲线法。

图9 等时应力-应变曲线Fig.9 Isochronous stress-strain curves

3.2.3.1 等时应力-应变曲线簇法

选取图5中1 h到71 h共8个时间节点的偏应力和应变绘制成等时应力-应变曲线(见图9)。曲线拐点对应的应力即为长期强度，该拐点为等时应力-应变曲线中线性段与非线性段的过渡点，依据经验判断选取[12-14]。从1 h到71 h，等时应力-应变曲线的非线性特征愈发显著，曲线逐渐偏向应变轴。

通过等时应力-应变曲线簇的拐点得到砂岩的长期强度，天然状态、饱水1 d和饱水5 d分别为28.12,26.74,21.95 MPa。

3.2.3.2 稳态蠕变速率与应力水平关系曲线法

利用幂函数和指数函数来分别拟合稳态蠕变速率与偏应力关系。绘制出稳态蠕变速率与应力水平的关系曲线，如图10所示。

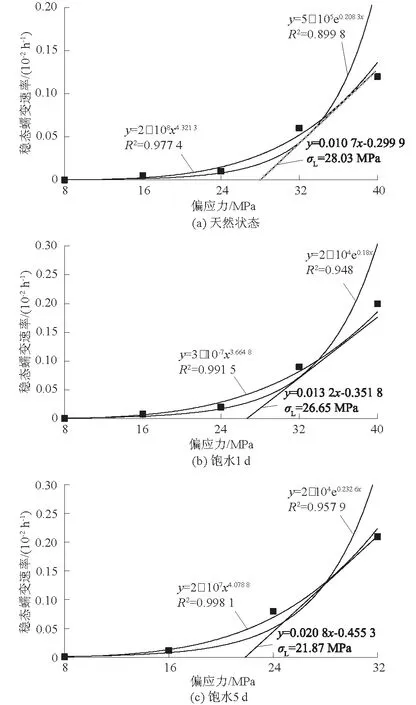
图10 稳态蠕变速率与偏应力关系曲线Fig.10 Relation between steady-state creep rate and deviatoric stress

由图10可知，稳态蠕变速率与应力水平呈幂函数关系，由此利用幂函数近直线段的切线在应力轴上的截距来确定长期强度[12]，天然状态、饱水1 d和饱水5 d的长期强度分别为28.03,26.65,21.87 MPa。利用该方法求取得的长期强度略小于通过等时应力-应变曲线簇法所求得的值。等时应力-应变曲线簇法过于依赖曲线拐点，选取拐点时具有一定的主观性和随意性，所以本文建议通过稳态蠕变速率与应力水平关系曲线法来确定砂岩长期强度。

砂岩长期强度随着饱水时间的增长而逐渐衰减。分析其原因为：长期强度可描述为砂岩进入加速蠕变阶段的破裂应力[15]，当岩石从稳定蠕变阶段进入加速蠕变阶段时，岩石内部逐渐形成了包括裂隙孔洞在内的应变集中区，抵抗变形的能力逐渐降低，以后裂隙孔洞的产生更加集中于这一区域[16]，而当岩石的含水率上升时，水充填到裂隙孔洞之中，使得岩石的应变软化性质更加明显，水的作用降低了进入加速蠕变阶段的破裂应力。

与瞬时强度相比，3种饱水条件下的长期强度分别为瞬时强度的64.12%,62.08%,59.34%，水的作用加剧长期强度衰减。砂岩的长期强度折减较大，水岩作用加剧长期强度的衰减，实际工程中应考虑长期强度折减问题，根据工程环境适当降低强度参数。

4 结 论

(1)随着饱水时间的增长和应力水平的提高，砂岩瞬时应变和蠕变量都呈递增趋势。随着含水状态的增强，蠕变量的增长幅度快于瞬时应变，含水状态的增强使得岩石的蠕变特性更加显著。

(2)随着饱水时间的增长，初始蠕变速率和稳态蠕变速率都逐渐增大。稳态蠕变速率与应力水平呈幂函数关系。水岩作用下岩石蠕变速率变化十分明显，可达数十倍增长。

(3)砂岩天然状态、饱水1 d和饱水5 d的长期强度分别为28.03,26.65,21.87 MPa，长期强度随着饱水时间的增长而逐渐衰减。实际工程中，尤其是长期受水作用影响下的岩石工程，应考虑长期强度折减问题。