大型渡槽实测钢筋应力定量与可靠性分析

(三峡大学 水利与环境学院，湖北 宜昌 443002)

1 研究背景

渡槽是水工建筑物中应用最广的一种立体交叉输水建筑物[1]。断面的选择上常采用U型断面，该结构是一种薄壁钢筋混凝土结构，具有外形简洁、受力明确等优点，但是在经过较长时间运行以后，由于受复杂环境因素的影响，槽身易出现裂缝、混凝土剥落等现象[2]。

目前国内外关于渡槽的报道多是关于结构优化和抗震等研究[3-4]，而关于渡槽监测的报道相对较少。近年来，随着我国南水北调工程开展，尤其是跨流域大型渡槽的修建，渡槽安全监测逐渐受到重视。一些大型渡槽通过安装预应力测力计、钢筋计等仪器来监测渡槽混凝土和钢筋应力应变的变化[5-6]。但从现有报道的文献来看，关于渡槽安全监测资料分析仍停留在定性分析阶段，很少建立安全监控模型进行定量分析。目前关于安全监测的研究多是针对大坝[7]，例如，Yu等[8]在大坝原型观测资料的分析方法和安全监控模型的建立方面做了大量的工作，取得了丰富的成果。显然，可以通过借鉴成熟的大坝安全监测的理论，用以研究渡槽监测模型及相应的监控指标。安全监测模型从理论上可以分为统计模型、确定性模型和混合模型。统计模型建模简单，拥有成熟的应用经验，所以在安全监测工作中得到了广泛的应用。但由于统计模型没有联系建筑物的结构性态，物理概念不明确[9]，有时需要结合数值分析方法建立确定性模型或混合模型。另外，广泛采用的最小二乘回归法易受各类变量间多重共线性的影响[10]，这些因素都会对实测资料的定量分析产生影响。针对上述问题，本文结合某大型渡槽开展了现场钢筋应力监测试验，接着对实测钢筋应力分别建立统计模型和混合模型，然后采用逐步回归法和复合形优化算法对上述模型进行参数估计，对分离出的各个分量进行定量分析，最后分析实测钢筋应力的可靠性。

2 渡槽钢筋计实测应力分析模型

2.1 钢筋计实测应力统计模型

统计模型数学概念明确，建模简单，是安全监测中常用的一种模型。运行期的大型渡槽实测钢筋应力按其成因可分为水压、温度和时效分量[11]，即

σ=σH+σT+σθ。

(1)

式中σH,σT,σθ分别为水压、温度、时效分量。当通水时间较短时，时效分量可以忽略不计，此时式(1)简化为

σ=σH+σT。

(2)

由渡槽的工作特性，选取钢筋计实测温度以及周期性谐波函数作为温度分量因子，当假设渡槽为简支梁结构时，水压荷载引起的应力与水深h的一次方成正比，即:

σH=x0+x1h;

(3)

(4)

式中:x0,x1为水压分量系数；x2,x3,x4为温度分量系数；ΔT为与测量基准时刻的温差；h为水深；t为时间。

2.2 钢筋计实测应力混合模型

由于统计模型是一种经验模型，当结构受力复杂且监测资料系列较短时，该模型精度一般。为此，有必要基于钢筋计实测应力建立混合模型。在混合模型中，水压分量采用有限元计算值的拟合表达式。由于有限元计算时的参数是假设的，与实际情况存在差异，则在水压应力分量拟合表达式前面乘一个调整系数x6。即混合模型为

σ=x5+σT+x6σH+σθ。

(5)

式中：x5为系数；σT为温度分量，仍采用统计模型表达式；σH采用有限元计算值的拟合表达式；当通水时间较短时，时效分量σθ可以忽略不计。故式(5)可简化为

σ=x5+σT+x6σH。

(6)

2.3 基于优化算法估计钢筋计实测应力模型参数

目前对于统计模型和混合模型，一般采用多元回归分析法或逐步回归分析法等最小二乘回归分析法来回归拟合这些模型的参数。最小二乘回归法易受各类因子变量间多重共线性的影响，为此，本文除了采用传统逐步回归分析法估计钢筋计实测应力数学监控模型参数外，还采用了复合形优化算法估计模型参数[12]。以钢筋计实测应力与数学监控模型计算应力的残差平方和为目标函数，选用复合形优化算法估计钢筋计数学监控模型参数的数学形式描述如下[13-14]：

求X=[x0,x1,x2,x3,x4,x5,x6]T,

(7)

使F(x)=f(X)=∑(σc-σm)2→min满足约束条件

(8)

但由于复合形法是一种常用的有约束优化算法，其基本思想是在可行域中选取k(n+1≤k≤2n)个设计点作为初始复合形的顶点，比较各顶点目标函数值的大小，去掉目标函数值最大的顶点(最坏点)。然后，以坏点以外其余各点的中心为映射中心，用坏点的映射点替换该点，构成新的复合形顶点。反复迭代计算，使复合形不断向最优点移动和收缩，直至收缩到复合形的顶点与形心非常接近，且满足迭代精度要求为止。为此，采用MatLab编写了基于复合形优化算法估计数学监控模型参数的计算程序,用于确定模型中各个系数[15]。

3 钢筋计实测应力可靠性分析流程

图1 实测钢筋应力可靠性 分析流程Fig.1 Flowchart of reliability analysis for measured steel bar stress

大型渡槽的工作性态复杂，而数学监控模型易受经验性和多重共线性的影响，导致钢筋计实测应力的可靠性难以判断。为此本文基于该大型渡槽中埋设钢筋计的实测应力，首先分别建立实测钢筋应力统计模型和混合模型，接下来分别采用逐步回归法和复合形优化算法对上述模型进行参数估计，分离获得水压分量和温度分量，最后分析评价分离分量是否符合一般力学规律，从而分析钢筋计测值是否具有可靠性。详细技术路线如图1所示。

4 实例分析

4.1 工程背景

某大型渡槽工程建于20世纪90年代，工程等级为Ⅲ级。渡槽上部结构为简支，下部结构为钢筋混凝土排架。该渡槽跨径10 m，设计流量14.54 m3/s，加大流量16.72 m3/s，槽身高2.7 m，槽身宽3.6 m。在该渡槽槽身跨中部位外缘钢筋上布置了2支BGK4911型振弦式钢筋计监测该渡槽的工作性态，钢筋计与纵向钢筋为串联方式焊接[16]，渡槽尺寸及钢筋计的安装布置如图2所示。

图2 钢筋计安装平面图Fig.2 Locations of steel bar strain meter

4.2 监测概况及监测结果

为了获得渡槽的工作性态，在现场开展了渡槽通水前后钢筋应力监测试验。该渡槽于2017年6月15日06:17开始通水，到08:23时渡槽水深h达到1.1 m，此后保持不变。使用振弦式读数仪在通水前2 h开始对2支钢筋计进行数据采集，采集时间间隔为1 h，获得读数和温度值，本次钢筋计应力监测至18:46结束。根据采集的模数和温度，计算得到钢筋实测应力。1#和2#钢筋计实测应力与温度过程线如图3所示。

图3 钢筋计实测应力与温度变化过程Fig.3 Change process of measured steel bar stress and temperature

由图3可见，钢筋计实测温度先略有下降，在07:24时降至最低，此时1#、2#钢筋计温度分别为23.8 ℃和23.4 ℃，实测拉应力达到最大，分别为1.203 MPa和1.118 MPa；随后，钢筋计实测温度逐渐升高，在 16:17时达到最高，此时1#、2#钢筋计温度分别为29.8 ℃和29.2 ℃，实测压应力达到最大，分别为-6.976 MPa和-4.416 MPa；随着环境气温的下降，钢筋计实测温度逐渐降低，此时实测压应力逐渐减小。

4.3 渡槽钢筋计实测应力定量分析

为更好地分析渡槽的工作性态，以下按第2节的原理，分别建立渡槽实测钢筋应力统计模型和混合模型，分离出各个分量，对渡槽的工作性态进行定量分析。

4.3.1 钢筋计实测应力统计模型建立

基于钢筋计实测应力，建立钢筋应力统计模型，然后分别采用逐步回归分析法、复合形优化算法对上述统计模型进行参数估计，得到1#、2#钢筋计的模型参数如表1所示。统计模型计算应力与监测应力对比如图4所示。

表1 不同方法的钢筋计实测应力统计模型参数估计Table 1 Estimation of statistical model parameters of measured steel bar stress by different methods

图4 钢筋计实测应力统计模型分析Fig.4 Analysis of measured steel bar stress by statistical model

由图4可知，1#钢筋计基于逐步回归法和复合形优化算法得到的统计模型计算值与实测值拟合效果良好，复相关系数分别为0.998 4和0.994 8；分离出的水压分量随着水深的增大而逐渐增加。当水深h稳定在1.1 m时，水压分量保持稳定。水深h由0增加到1.1 m的过程中，逐步回归法、复合形法2种方法分离得到的水压分量增量分别为1.720 MPa和1.375 MPa。2#钢筋计基于逐步回归法和复合形优化算法得到的统计模型计算值与实测值拟合效果良好，复相关系数分别为0.973 4和0.953 8；但是基于逐步回归法得到的统计模型分离出的水压分量随着水深的增大，始终为0；基于优化算法得到的水压分量与水深h成正相关，水深h由0增加到1.1 m的过程中，水压分量增加了0.262 MPa。

4.3.2 钢筋计实测应力混合模型建立

由于统计模型属于数学经验模型，未能较好地联系渡槽实际的结构性态，所以接下来采用2.2节的原理，建立渡槽实测钢筋应力混合模型进行分析。

4.3.2.1 渡槽有限元模型建立

依据该渡槽的几何尺寸参数，建立整体三维有限元模型。对于混凝土采用六面体八节点等参单元，对于钢筋网则采用三维杆单元；由于渡槽钢筋网十分密集，而且钢筋直径大小不同，为此，采用通用有限元MSC.MARC软件中的内嵌钢筋功能，即建立好“钢筋网”单元后，用“INSERTS”功能将钢筋网单元嵌入混凝土单元，在计算过程中，假设钢筋网和混凝土之间的位移协调。如图5所示，该渡槽共有50 585个单元，58 540个节点；其中，六面体八节点单元40 155个，钢筋杆单元10 430个。在渡槽槽身内表面作用水压荷载，并假设渡槽端部混凝土的底部为完全位移约束。

图5 渡槽有限元模型Fig.5 Finite element model of aqueduct

4.3.2.2 混合模型水压分量表达式

结合上述建立的渡槽有限元模型，假设渡槽混凝土和钢筋的材料参数取设计值，分别计算不同水深下渡槽钢筋计位置的钢筋应力，然后对1#、2#钢筋计位置的计算钢筋应力和槽身水深进行多项式拟合，即：

σH1=1.021 7h-0.617 2 ；

(9)

σH2=0.324 5h2+0.422 1h-0.088 5 。 (10)

式中:σH1,σH2分别为1#、2#钢筋计有限元计算应力值；h为渡槽水深。

由式(10)可见，虽然渡槽整体为简支结构，但局部为壳体结构，导致2#钢筋计的应力与渡槽水深的关系更接近于二次多项式。

4.3.2.3 混合模型参数估计

由于材料参数设计值与实际值存在差异，为此基于实测数据，引入调整系数建立钢筋应力混合模型，然后分别采用逐步回归分析法、复合形优化算法对上述混合模型进行参数估计，得到1#、2#钢筋计的模型参数如表2所示。1#、2#钢筋计实测应力和混合模型拟合应力对比如图6所示。

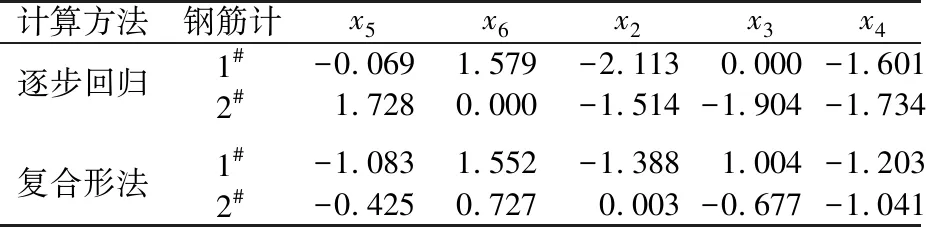
表2 不同方法估计的钢筋计实测应力混合模型参数Table 2 Estimation of mixed model parameters of measured steel bar stress by different methods

图6 钢筋计实测应力混合模型分析Fig.6 Analysis of measured steel bar stress by mixed model

由图6可知，1#钢筋计基于逐步回归法和复合形优化算法得到的混合模型计算值与实测值拟合效果良好，复相关系数分别为0.998 4和0.995 8；分离出的水压分量随着水深h的增大而逐渐增加。当水深h稳定在1.1 m时，水压分量保持稳定。水深h由0增加到1.1 m的过程中，逐步回归法、复合形法2种方法分离得到的水压分量增量分别为1.720 MPa和1.690 MPa。2#钢筋计基于逐步回归法和复合形优化算法得到的混合模型计算值与实测值拟合效果良好，复相关系数分别为0.966 3和0.920 3；但是基于逐步回归法得到的统计模型分离出的水压分量随着水深的增大，始终为0；而基于优化算法得到的水压分量与水深h成正相关，水深h由0上升到1.1 m的过程中，水压分量增加了0.623 MPa。

4.4 钢筋计实测应力可靠性分析

该渡槽运行期较长，且工作性态较为复杂，统计模型和逐步回归法易受经验性和多重共线性的影响。因此，根据4.3节的渡槽工作性态定量分析的结果，对1#、2#钢筋计实测应力可靠性分析如下：1#钢筋计通过不同方法分离出的水压分量增量大体保持一致，但是2#钢筋计通过不同方法分离出的水压分量增量未呈现出规律性。为此，在表3中分别给出了1#、2#钢筋计计算应力变化情况以及不同模型和方法分离出的水压分量变化情况。

表3 不同模型和方法分离出的水压分量对比
Table 3 Comparison of water pressure component indifferent models by different methods

钢筋计模型钢筋应力增量 /MPa水压分量增量/MPa水深h由0 m上升到1.1 m水深h由0 m上升到0.5 m水深h由0 m上升到1.1 m逐步回归优化算法逐步回归优化算法逐步回归优化算法1#2#统计模型1.1570.9820.7820.6261.7201.375混合模型1.1570.9280.7820.7681.7201.690统计模型0.7870.7460.0000.1190.0000.262混合模型0.4600.8090.0000.2120.0000.623

由表3可知：

(1)1#钢筋计通过统计模型与混合模型计算得到的钢筋应力与实测值吻合良好，钢筋应力增量在水深h由0上升到1.1 m的过程中表现出较强的规律性；水压分量增量在水深h由0上升到0.5 m与由0上升到1.1 m的过程中也基本保持一致；由此认为1#钢筋计测值正常。

(2)2#钢筋计通过统计模型和混合模型分离得到的钢筋应力与实测值吻合良好。但通过2种模型计算得到的钢筋应力增量在水深h由0上升到1.1 m的过程中相差较大。在水深h由0上升到0.5 m与由0上升到1.1 m的过程中，逐步回归得到的水压分量增量为0，优化算法得到的水压分量虽不为0，但是也相差较大，与1#钢筋计得到的结论不一致，故判断2#钢筋计测值异常，不具有可靠性。

5 结 论

(1)本文基于钢筋计实测钢筋应力，分别建立了应力统计模型和混合模型，然后分别采用逐步回归法和复合形优化算法对上述模型进行了参数估计。分析表明：1#、2#钢筋计基于不同计算方法得到的统计和混合模型拟合效果较好。

(2)通过2支钢筋计分离得到钢筋应力增量与水压分量增量发现：1#钢筋计在水深h变化过程中，通过不同计算方法得到的钢筋应力增量基本保持一致；水压分量增量在水深h变化过程中也基本保持一致，认为1#钢筋计测值正常；2#钢筋计在水深h变化过程中，通过不同计算方法得到的钢筋应力增量相差较大；在水深h由0上升到0.5 m与由0上升到1.1 m的过程中，通过逐步回归分析法分离得到的水压分量增量为0；通过复合形优化算法分离得到的水压分量增量相差较大，与1#钢筋计得到的结论不一致，由此认为2#钢筋计测值异常，不具有可靠性，故该钢筋计测值不可用于分析渡槽的实际工作性态。