基于现场试验数据分段的岩基抗剪强度参数概率统计分析方法

(1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072； 2.中国建筑第七工程局有限公司，郑州 450000； 3.中国电建集团华东勘测设计研究院有限公司，杭州 310000)

1 抗剪强度参数统计分析方法现状及存在的问题

岩基抗剪强度参数是岩基上建筑物进行抗滑稳定审核的重要设计指标。研究确定岩基抗剪强度参数的均值、变异系数与概率分布等概率特性对工程抗剪强度参数设计值的合理取定、结构安全可靠度分析、工程风险分析以及设计规范修编都是至关重要的[1]。

长期以来，人们对岩基抗剪强度参数的确定进行了大量的研究工作。迄今，现场原位抗剪试验因其较室内中小型直剪试验能反映更多的岩体结构特征，试块剪切断面较大,试验结果可靠性较高，仍然是工程确定岩基材料抗剪强度参数的主要方法。由于岩基材料为天然材料，试块抗剪试验结果存在较大的离散性，由抗剪试验结果确定抗剪强度参数的概率分布及均值、变异系数等概率特性的方法归纳主要有以下几种。

1.1 传统分组法

传统分组法[2-4]是工程设计人员、众多研究者采用的主要方法，该方法是在地基每一主要地质单元内布置不少于4组的野外试验，其中每一组试块数不少于4个，试验后按摩尔-库伦准则回归得到各组的摩擦系数与凝聚力，然后再把不同组的摩擦系数与凝聚力结果按常规统计方法分析摩擦系数与凝聚力的概率分布与均值和方差等统计参数。这种分组法存在若干问题或不足：①因为分组摩擦系数与凝聚力是由各组试块抗剪强度的平均值求得的，传统分组法不能反映或者说抹去了各组内试块抗剪强度的离散性；②设想当各分组内的试块数逐渐增多时，由于各试块来自同一地质单元，亦即可认为来自同一概率母体，根据概率论，各组试验所得的抗剪强度平均值一定趋于相同，也就是说各分组摩擦系数与凝聚力从理论上是趋于相同的，没有离散性，如此再由它们来确定摩擦系数与凝聚力的概率分布与均值和方差等统计参数，从理论来上讲显然是不合适的；③在水利水电工程中，因现场原位抗剪断试验成本高，试验条件困难，一个工程所做的现场分组试验数往往较少(中、小工程一般不做上述试验)，分组样本数通常难以满足统计计算精度要求。

1.2 试块法

试块法是由试块抗剪试验数据——剪切面正应力和剪应力直接计算摩擦系数与凝聚力均值、方差等统计参数的方法。因一个试块就是一个样本，相对于一组是一个样本的传统分组法，该法相当于扩增了抗剪强度参数统计分析的样本数，其样本数是分组法的4倍以上(按每一组试块数不少于4个计算)。

目前该法主要有直接或基本套用数理统计学中一元线性回归公式的线性回归法(或称点群中心法、最小二乘法)[5-6]、简化相关法(或称τ平均法)[7-9]和文献[10]方法。

国内有不少文献[5-6]是直接采用概率论中线性回归法的相关公式来进行岩基抗剪断强度参数的统计分析的。采用这种线性回归法来求摩擦系数与凝聚力的均值不存在问题，但如果继续采用该方法中2个回归系数的估值误差方差公式来计算摩擦系数与凝聚力的方差则存在问题：当样本容量m较小时，该方法看似能得到一个较为合理的摩擦系数与凝聚力方差，但随着m增大，摩擦系数与凝聚力的方差都将趋近于0，这显然是不正确的。其问题在于不妥地把摩擦系数和凝聚力等同于一元线性回归方程中的2个回归系数，将有限样本数导致的2个回归系数的统计不确定性误当成抗剪强度指标的真实不确定性看待[11]。

简化相关法，又称τ平均法，是国内港口工程规范方法，广泛应用于地基土抗剪强度指标的统计分析。根据简化相关法计算的摩擦系数与凝聚力均值与传统分组法计算的结果接近，而方差则是在假设摩擦系数与凝聚力相互独立的基础上通过线性回归得到的，该法不能考虑摩擦系数与凝聚力的相关性问题。由于简化相关法通过一系列不同正应力下求得的试块抗剪强度方差来回归计算摩擦系数与凝聚力的方差，亦即需要计算各级压力下试块抗剪强度的标准差,要求的试验试块较多，不适用于水电工程原位岩基抗剪试块少、不能给出多个正应力下的试块抗剪强度方差的情况。文献[12]认为简化相关法理论依据不完备，实用时可能得到不合理的结果，不宜在工程中推广使用或需进行修正。

针对水电工程抗剪试验的特点，笔者在文献[10]中基于数理统计理论提出了一种抗剪强度参数统计计算方法，该法在推导过程中假定摩擦系数与凝聚力相互独立，故不能用于摩擦系数与凝聚力存在相关性的情况。

1.3 可靠度分析法

可靠度分析法[13-14]采用最大似然准则，认为单个抗剪试块的摩擦系数与凝聚力除满足摩尔-库伦准则外，还补充一个假定：认为试块的摩擦系数与凝聚力为出现概率最大的数值。如此即有2个求解摩擦系数与凝聚力的条件，按可靠度方法就可计算出单个抗剪试块的摩擦系数与凝聚力。笔者认为，由概率论随机变量抽样方法来看，对于一个随机变量的一次抽样值，尽管从大数上讲要满足其总概率分布值，但单次抽样值显然是充满着随机性的，不能保证该抽样值的出现概率最大。因此，该法采用最大似然准则假定是否合理值得商榷。另外，该方法也未曾见过相应的验证。

为此，本文根据岩基现场抗剪试验特点，依据剪切面正应力大小将试验数据适当分段，采用数理统计理论，推导提出可以考虑摩擦系数与凝聚力相关性的新的抗剪强度统计参数计算公式。同时结合线性代数正交变换理论，构造提出验证试块法的计算机随机模拟测评方法，对有关试块法进行计算测评分析，论证本文提出的新公式的正确性,并探讨提出本文试块法所需的最少试块数量。最后通过工程应用，给出岩基材料摩擦系数与凝聚力的若干统计特点。

2 岩基抗剪断强度概率统计参数计算方法研究

2.1 计算公式

(1)

(2)

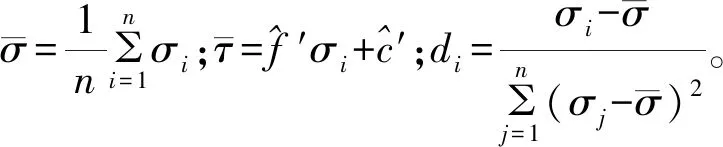
(3)

f′,c′的相关系数ρf′c′为

(4)

当f′,c′不相关时，则需将现场抗剪试验数据(σ1，τ1),(σ2，τ2) ,…,(σn，τn)依剪切面正应力从小到大分成2段，由式(3)即可退化得到f′,c′在无相关模式下的方差计算公式为

(5)

2.2 基于随机模拟的试块法计算机验证方法

2.2.1 试块法随机模拟测评方法的构建

随机模拟又称蒙特卡罗(Monte-Carlo)或统计试验方法[15]。根据概率理论和线性代数，构造提出的计算机随机模拟测评方法步骤如下。

(1)确定摩擦系数与凝聚力的抽样公式。根据概率论随机模拟方法和线性代数正交变换理论，结合随机变量经线性变换后其相关系数的绝对值不变的定理，可推导出分别服从正态分布和对数正态分布的摩擦系数f′与凝聚力c′的抽样公式为

(6)

其中：

式中：e是自然常数；y是c′的自然对数；μlnc′和σlnc′分别为c′的自然对数lnc′即y的均值和标准差；u1，u2，u3，u4分别为4个相互独立的在[0,1]区间上服从均匀分布的随机数。

如果摩擦系数f′与凝聚力c′均服从对数正态分布，则它们的抽样公式为

(7)

(2)利用式(6)或式(7)进行摩擦系数与凝聚力的n次抽样，得到摩擦系数与凝聚力的n对样本(f′i,c′i)(i=1，2，…，n)。同时在正应力试验范围内随机抽取n次正应力值σi。

(3)由样本(f′i,c′i)及正应力σi，根据Mohr-Coulomb准则，可得一系列模拟试块抗剪试验数据(σi,τi)(i=1，2，…，n)，其中τi=f′iσi+c′i。

(4)由模拟抽样得到的抗剪试验数据 (σi,τi)(i=1，2，…，n)，采用有关试块法计算摩擦系数与凝聚力的均值、方差与相关系数等统计特征量。

(5)比较摩擦系数与凝聚力的模拟计算均值、方差与相关系数等与原设定值的差别，对有关统计参数计算方法进行评价。

显然，如果将上述第(4)步改成用其他考虑了试块抗剪强度离散性的统计分析方法[13-14]来计算摩擦系数与凝聚力的统计特征量，这里提出的计算机验证方法也适用于它们的验证工作。

2.2.2 随机模拟测评算例

针对摩擦系数与凝聚力不相关和相关2种模式，由随机模拟得到的试块抗剪试验数据(σi,τi)(i=1，2，…，n)，应用本文方法和文献[5]、文献[6]中的方法计算的抗剪强度参数均值、方差与相关系数见表1、表2，其中设定值为参数预设值，而随机抽样值则由各f′,c′抽样值计算得来。从表中看出参数随机抽样值接近设定值，说明f′,c′的抽样次数是足够的。

表1 f′和c′不相关模式下n=50万次抽样 模拟计算的统计参数Table 1 Simulated values by 5×105 sampling when f′ is not related to c′

表2 f′与c′相关模式下n=50万次抽样 模拟计算的统计参数(相关系数=0.5)Table 2 Simulated values by 5×105 sampling(when the correlation coefficient of f and c is equal to 0.5)

由表1和表2可见：

(1)各试块法计算的摩擦系数与凝聚力均值相同，且非常接近原设定值。说明采用各试块法计算摩擦系数与凝聚力均值是没有问题的。

(2)当摩擦系数与凝聚力不相关时，对于摩擦系数与凝聚力的变异系数，按本文提出的新公式，不论是应用相关时的公式还是不相关时的公式，得到的计算值与原设定值基本一致，而按文献[5]和文献[6]公式得到的计算值极小，接近于0，与原设定值相差甚远，计算结果不可用。

而当摩擦系数与凝聚力存在相关性时，只有应用本文提出的相关情况下的计算式(3)才可以得到与参数设定值接近的结果。

因此，通过这里具体算例的测评工作，验证了本文新公式的正确性，并表明文献[5]和文献[6]有关公式是不能被用于岩基摩擦系数与凝聚力的变异系数和相关系数计算的。

表3 较好岩类试块总数与置信度关系(M=105)
Table 3 Relation between test block number and confidence coefficient for good quality rock (M=105)

f′,c′相关性相对误差不同试块总数下的抗剪强度小值平均值置信度/%10 15 20 30 40 50 60 70 相关不相关0.281.3391.0595.5798.1299.0899.34099.7499.930.150.9565.0374.7585.6990.7994.62096.2597.200.284.9795.2398.6299.3399.9899.9990.156.7869.8681.1492.3296.3398.39099.4699.77

表4 较差岩类试块总数与置信度关系(M=105)
Table 4 Relation between test block number and confidence coefficient for inferior quality rock (M=105)

f′,c′相关性相对误差不同试块总数下的抗剪强度小值平均值置信度/%10 15 20 30 40 50 60 70 相关不相关0.267.6383.7889.9194.3997.7698.4898.6499.240.141.7354.4267.0678.9584.7688.8091.4292.180.272.2687.7993.3597.9399.2299.9299.9899.990.145.8957.5068.0579.9387.6191.5294.1195.17

2.3 试块法要求的试块总数探讨

采用试块法计算分析摩擦系数与凝聚力的统计参数时，试块总数对统计分析结果有何影响是一个很有意义的问题，对这个问题还未见到过有相关的国内外研究文献。因式(3)、式(5)需求解方程组，无法参考现有数理统计理论及岩土单个物理力学指标最小样本数成果来解决本文提出公式所需试块数目的问题。

分析本文提出的随机模拟测评方法，可以发现本文2.2.1节第(1)步—第(4)步内容所计算出来的材料均值、变异系数和相关系数，就是n个试块下的材料参数均值、变异系数和相关系数的一个样本。因此可以设想如果重复第(1)步—第(4)步工作M遍，显然就可以分别得到摩擦系数与凝聚力均值、变异系数和相关系数等指标的M个样本。当M足够大时，由这M个样本就可计算出摩擦系数与凝聚力均值、变异系数和相关系数等指标的置信度。再由置信度结果，即可探讨试块样本数目对统计参数等指标的影响，解决试块法所需最小试块总数的问题。

从经济和目前现场试验可以实现的角度出发，本文将通过计算分析反映摩擦系数与凝聚力组合效果且工程常用的抗剪强度小值平均值置信度随试块总数的变化，来研究最小试块总数问题，因为计算分析发现以材料变异系数、相关系数达到一定置信度要求的最小试块总数太多，是工程难以做到的(因篇幅限制，相关计算成果未列出)。

通过对较好岩类和较差岩类计算，各试块总数下的抗剪强度小值平均值置信度见表3、表4。其中对较好岩类，摩擦系数与凝聚力均值分别取1.0和1.1 MPa，而变异系数分别取0.2和0.35，相关时摩擦系数与凝聚力的相关系数取0.3。对较差岩类，摩擦系数与凝聚力均值分别取0.7和0.4 MPa，而变异系数分别取0.3和0.6，相关时摩擦系数与凝聚力的相关系数取-0.7。

由表3和表4可见，抗剪强度小值平均值的置信度随试块数目的增加而逐渐趋近于100%。在同样试块总数下，相关情况的置信度低于不相关情况，或者说相关情况下的最小试块数目要高于不相关情况，以及抗剪强度参数变异系数大的最小试块数目也要高于变异系数小的。若以抗剪强度小值平均值满足要求为标准，对较好岩类，如果允许相对误差取0.1，在摩擦系数与凝聚力相关情况下，按90%置信度要求的最小试块总数约为40块；而不相关情况下需要的试块总数要少些，约为30块。对较差岩类，因变异系数大，在同样置信度下需要的试块总数比较好岩类多，在摩擦系数与凝聚力相关情况下，要求的最小试块总数达55块；而不相关下需要的试块总数约为45块。

如果允许相对误差取0.2，对较好岩类，相关和不相关情况下要求的试块总数则约为15块；对较差岩类，相关和不相关情况下要求的试块总数约为20块。

表5 混凝土与基岩胶结面抗剪断强度参数统计分析成果Table 5 Statistical analysis results of shear strength parameters of concrete/bedrock cement surface

表6 Ⅱ、Ⅲ、Ⅳ类岩体抗剪断强度参数统计分析成果Table 6 Statistical analysis results of shear strength parameters of class II, III, and IV rock

3 工程岩基抗剪强度参数的统计计算分析

本节应用文献[4]列出的现场抗剪试验数据，采用本文所提试块法及传统分组法，对各类岩基材料的抗剪强度参数进行了一系列统计计算分析，部分成果列于表5和表6。其中抗剪断强度均值、标准差及变异系数是取工程原位试验正应力的中间值计算的。

通过对计算结果(表5和表6)的分析，可见岩基抗剪强度参数具有以下统计特点：

(1)不论是用试块法还是分组法，所得凝聚力的变异系数大多要比摩擦系数的大。采用试块法和分组法得到的摩擦系数与凝聚力及抗剪强度的均值相差不大，而由试块法得到的变异系数则大多要比传统分组法的大。

(2)对于混凝土与基岩的胶结面和岩体，随着基岩质量由好变差，相应的摩擦系数与凝聚力变异系数一般来说也要变大。而对于其摩擦系数与凝聚力的相关性问题，从试块法计算成果来看，对Ⅰ类、Ⅱ类岩基，已计算的2个工程的摩擦系数与凝聚力的相关系数分别为0.090和0.026，摩擦系数与凝聚力呈极弱的正相关；对Ⅲ、Ⅳ、Ⅴ类岩基，已计算的8个工程的摩擦系数与凝聚力的相关系数都为负值，平均为-0.87，摩擦系数与凝聚力呈强负相关性。

采用分组法时，因工程原位抗剪试验分组样本数太少，计算呈现的摩擦系数与凝聚力的相关性统计规律不好。

(3)对比抗剪强度的变异系数可见，采用相关模式试块法与采用无相关模式试块法计算的抗剪强度变异系数比较接近。这个数值结果与前面的理论分析一致。

4 结 语

(1)本文依据精度相近亦即试块数相近原则，通过对现场抗剪试验数据适当分段，基于数理统计理论，推导提出了由现场抗剪试块正应力和剪应力直接计算岩基摩擦系数与凝聚力统计参数的新公式。

(2)根据现场抗剪试验特点，结合概率论随机模拟方法与线性代数正交变换理论，构造并提出了一种验证试块法的计算机随机模拟测评方法。通过应用该法，对有关试块法进行了计算测评分析，论证了本文提出公式的正确性。本文所提计算机随机模拟测评方法也可用于其它考虑了试块抗剪强度离散性的摩擦系数与凝聚力概率统计方法的验证工作。

(3)以抗剪强度小值平均值满足要求为标准，探讨提出了本文试块法所需的最少试块数量。当允许相对误差取0.1时，最小试块总数约为30～55块；而允许相对误差取0.2时，最小试块总数约为15～20块。其中，对较好岩类和摩擦系数与凝聚力不相关情况取偏小值，对较差岩类和摩擦系数与凝聚力相关时则取偏大值。

(4)一般来说，用试块法计算的摩擦系数和凝聚力的变异系数要比传统分组法的大。对于Ⅰ类、Ⅱ类较好岩基上的混凝土与基岩的胶结面和岩体，抗剪摩擦系数与凝聚力呈极弱的正相关，在进行抗剪强度参数统计分析时，是否考虑相关模式对结果的影响不大；而对于Ⅲ类以下的岩基，因摩擦系数与凝聚力则呈强负相关性，是否考虑相关模式对抗剪强度参数的变异系数影响则比较明显。

(5)因两者计算的抗剪强度变异系数基本一样，从便于工程应用的角度考虑，在试块数不多的情况下，可以用无相关模式公式替代相关模式公式做统计计算分析。

(6)由于现场抗剪试块数有限以及试验结果存在随机性，如果分段试验数据后段试块的抗剪强度离差平方和偶尔出现比前段试块抗剪强度离差平方和还要小时，因与理论上抗剪强度方差一般是随剪断面正应力增加而增加相反，计算的材料抗剪参数方差可能出现负值，此时本文提出的方法不适用。