台球桌上的秘密——最短路径问题

文陈玲玲

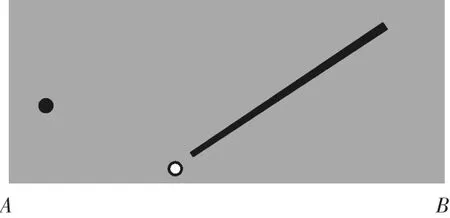
【问题情境】如图，台球桌上有一个白球、一个红球，如何用球杆去击白球，使其撞到AB边反弹后再撞到红球？

【思路解析】台球桌上隐藏的秘密实际上是“光线反射”原理，在数学上反映的是“利用轴对称，求最短路径”的本质问题。建构数学模型：如图1，已知点M、N在AB的同侧，在AB上找一点D，使得MD+ND的和最小。

图1

这就需要我们利用轴对称的知识，作点M关于AB的对称点M′，然后连接M′N，与AB的交点即为D点，如图2。

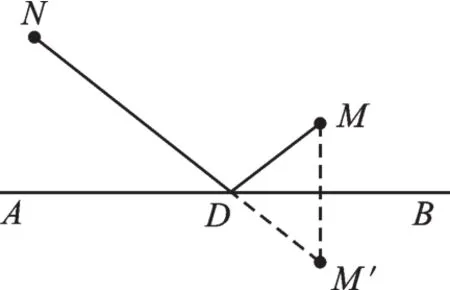
图2

例 如图3，点A是锐角∠MON内部任意一点，在∠MON的两边OM、ON上各取一点B、C，组成三角形，使三角形周长最小。

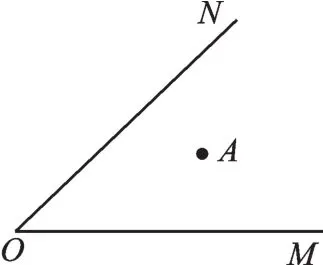
图3

图4

【思路解析】如图4，作点A关于OM的对称点A1、关于ON的对称点A2，连接A1A2。A1A2与OM的交点即为B点，与ON的交点即为C点，此时△ABC的周长最小。

【变式训练】如图5，点P、Q是锐角∠MON内部任意两点，在∠MON的两边OM、ON上各取一点B、C，组成四边形，使四边形周长最小。

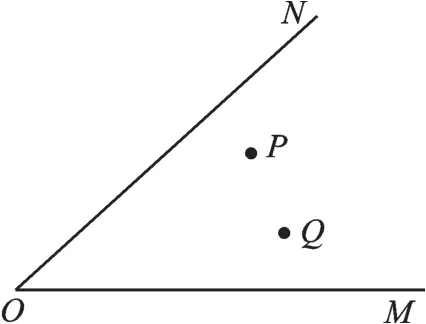
图5

【思路解析】如图6，作点Q关于OM的对称点A1，作点P关于ON的对称点A2，连接A1A2。A1A2与OM的交点即为B点，与ON的交点即为C点，此时，四边形PQBC的周长最小。

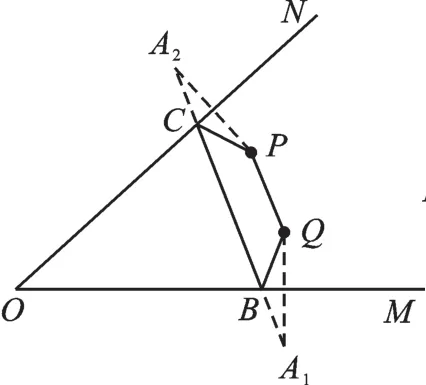
图6

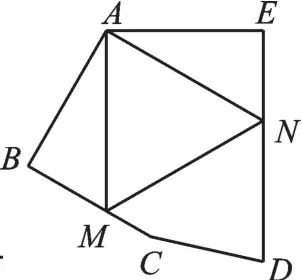
图7

【拓展提升】如图7，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，在BC、DE上分别找一点M、N，使得△AMN的周长最小，则∠AMN+∠ANM= ________。

【思路解析】如图8，作点A关于BC的对称点A1，作A关于DE的对称点A2，连接A1A2，与BC的交点为M，与DE的交点为N，此时△AMN的周长最短。

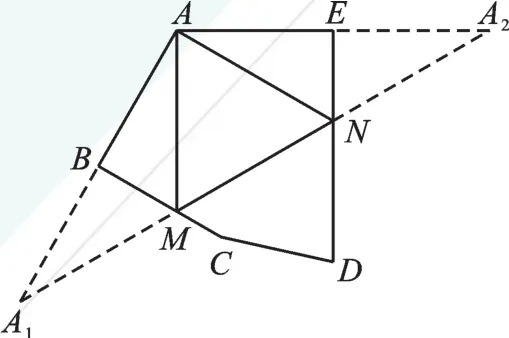
图8

由对称可知，∠BAM=∠A1，∠NAE=∠A2。

在△AA1A2中，∵∠A1AA2=120°，∴∠A1+∠A2=60°。

又∵∠AMN=∠BAM+∠A1=2∠A1，∠ANM=∠NAE+∠A2=2∠A2，

∴∠AMN+∠ANM=2∠A1+2∠A2=120°。

【拓展提升】如图9，点A是锐角∠MON内部任意一点，在射线ON上取一点B，使BA与点B到射线OM的距离之和最短。

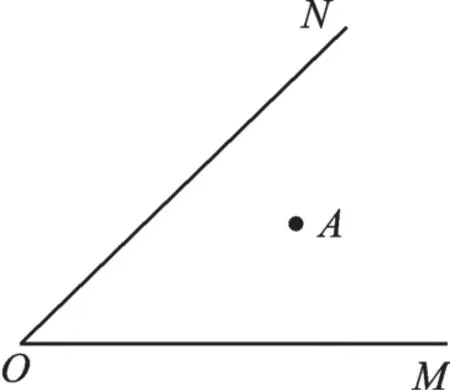
图9

图10

【思路解析】

思路一：如图10，作点A关于ON的对称点A1，过点A1作OM的垂线段A1C，交射线ON于点B。

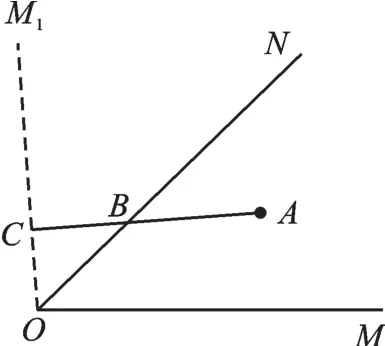
图11

思路二：如图11，作射线OM关于ON对称的射线OM1，过点A作射线OM1的垂线段AC，交射线ON于点B。