基于加权最小二乘的声相关计程仪速度精确估计

闫善勇，赵二亮，邱薇，王长红

基于加权最小二乘的声相关计程仪速度精确估计

闫善勇1,2，赵二亮1,3，邱薇1,3，王长红1,3

(1. 中国科学院声学研究所海洋声学技术中心，北京 100190；2. 中国科学院大学，北京 100049；3. 北京市海洋声学装备工程技术研究中心，北京 100190)

声相关计程仪首先利用加权最小二乘法确定目标函数，然后通过序列二次规划法估计速度。考虑海底混响数据时空相关函数宽度的减小、相关系数点与相关函数中心点间距的增大，都会导致相关系数的均值减小、分布范围增大，此时相关系数在目标函数中对应项的权重也应当减小。在这样的前提下，引入调节参数，调节权重函数的宽度，使设备在各个速度下测速相对偏差的一致性达到最优，提高速度估计精确度。调节参数在设备标定与验证试验中确定，不同的设备可能具有不同的调节参数。试验数据证明了该方法对不同声相关计程仪测速精确度的提高都有效果。

声相关计程仪；加权最小二乘；序列二次规划；测速精确度

0 引言

声相关计程仪(Acoustic Correlation Log, ACL)基于“波形不变性”原理，通过理论相关函数与数据相关函数的匹配(均方误差最小意义下的逼近)，估计理论模型参数，获得速度估计[1-3]。相比于声多普勒计程仪，声相关计程仪有如下优点：(1) 垂直向下发射宽波束，受载体纵摇和横摇的影响较小；(2) 相同大小的换能器，发射声波的频率可以更低，作用距离更大；(3) 速度估计与声速无关[4-7]。目前，声相关计程仪面临的主要问题是测速精确度较声多普勒计程仪低。为了提高声相关计程仪的测速精确度，冯雷[8]提出包含宽度调节系数的指数型理论相关函数，尽管对混响物理性质的解释上有所欠缺，但形式简单，便于实时运算；蒯多杰[9]在使用最小二乘法进行目标函数计算时实施了自适应加权，权值来自于经过修正的理论相关函数的值，同时，在理论相关函数中引入了幅度调节因子；易卉芹等[10]通过增加两个椭圆因子将理论相关函数转变为椭圆形，使其与椭圆形数据相关函数拟合得更好；王映春等[11]利用延时为0的理论和数据相关函数估计接收阵元的声学中心，减小阵元坐标误差。国外，KEARY等[2]对声相关计程仪进行了仿真，分析了影响海底混响时空相关特性的因素。BOLTRYK等[12-13]分析了现有峰值估计技术对设备速度估计精确度和精密度的影响，并在此基础上提出利用径向基函数法和高斯过程法估计落在测量区域边缘的峰值点，提高设备工作稳定性。ANTHONY等[14-16]通过设计声相关计程仪接收阵等方法提高设备工作的性能。

本文介绍了声相关计程仪速度估计的基本原理及解算流程，给出数据相关系数的分布特征及其对应的相关系数权重计算方法，引入权重调节参数，提高设备速度估计相对偏差的一致性。此外还指明了声相关计程仪测速精确度改进的方向。

1 声相关测速技术

1.1 基本原理

海底混响的理论时空相关函数[8]：

式中，代表相关函数最大值点。也就是说，在已知两信号间时延的情况下，确定相关函数最大值点即可估计出速度，这就是“波形不变性”原理在声相关计程仪上的应用。为此利用平面阵在多个位置接收海底混响信号，再将信号两两时延相关，作为两接收基元间距处的相关函数采样。在采样数目足够时，即可利用最小二乘法估计包含载体x、y方向速度在内的理论相关函数模型参数。

1.2 速度解算流程

根据1.1节中声相关测速的基本原理，ACL速度解算的流程如图2所示[9]。多个接收基元接收到混响信号后，进行时延相关获得数据相关系数。

图2 ACL速度解算流程

目标函数由加权最小二乘法(Weighted Least Square, WLS)根据理论和数据相关系数得到[9]：

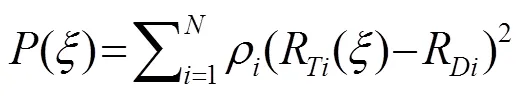
在确定目标函数后，利用最优化算法中的序列二次规划法(Sequential Quadratic Programming, SQP)进行目标函数的最大值点估计[17-18]。估计结果中包含载体的、方向速度。

2 相关系数分布特征及权重计算

2.1 相关系数分布特征

如图1所示，相关函数在相关平面上表现为钟形，定义相关系数=0.707时对应的宽度为相关函数宽度，用来判断相关函数的变化情况。由式(1) 推导可得：

根据ACL接收基元的排布，可以获得多种空间间隔的相关系数，它们构成对该试验条件下相关函数的采样。在相关函数最大值点附近，相关系数的分布范围较小，随着与相关函数最大值点距离的增大，相关系数的分布范围逐渐增大，如图4所示。图4是湖上试验中2 366帧数据的计算结果，圆圈表示相关系数均值，误差棒表示相关系数标准偏差，曲线表示利用相关系数均值拟合的相关函数结果，试验中载体速度9.04 kn，相关时延1.83 ms，图4中曲线最大值点位置-0.017 m。另外，海上试验中，相关系数的分布范围相比于湖上试验更小，这与其较大的相关函数宽度、较大的相关系数有关。从相关系数分布的角度来说，在同一相关函数条件下，距离相关函数中心点越近的相关系数可信度越高，越应该被分配较大的权重；在不同的相关函数条件下，相关函数越宽，相关系数值越大，相关系数分布范围越小，越应当被分配较大的权重，或者说，相关系数间权重的分配应该越均衡，权重之间的差距应该越小。

(a)=1.397 2

(b)=1.433 4

(c)=0.848 4

(d)=0.737 1

图3 不同相关函数宽度情况下速度估计的结果比较

Fig.3 Comparison of the velocity results under different widths of correlation function

2.2 权重计算方法

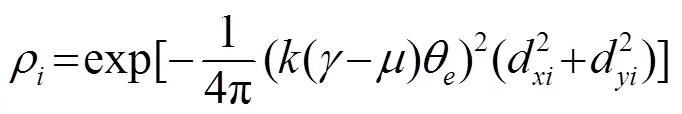
式中，是一个调节参数。此时，相关函数宽度增大，权重值增大，权重间的差距变小。

3 权重调节及试验结果

2015～2017年间，在某湖上进行了9套70 kHz ACL的标定与验证试验，本文重新对数据进行处理，采用式(7)进行权重计算。已知湖底深60 m左右，试验船航速5～10 kn，调节参数在-1.8～3.6之间变化。对同一套设备，选定不同的调节参数，观察不同速度下，速度估计相对偏差的变化情况，图5显示了1#～4#ACL的数据处理结果。

(a) 1#ACL

(b) 2#ACL

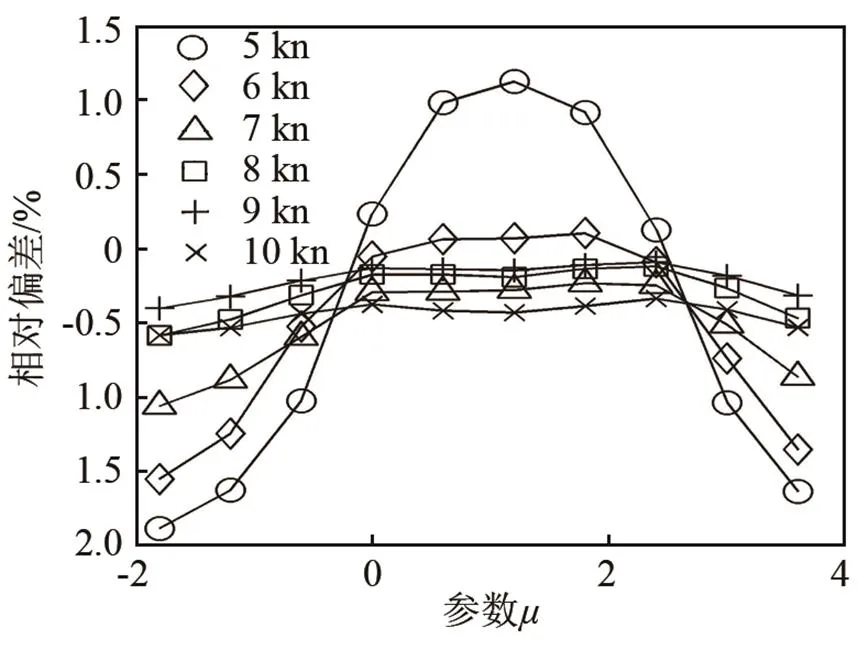
(c) 3#ACL

(d) 4#ACL

图5 各速度下测速相对偏差随调节参数的变化情况

Fig.5 Variation of the relative deviation of velocity measure- ment with the adjustable parameter

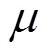
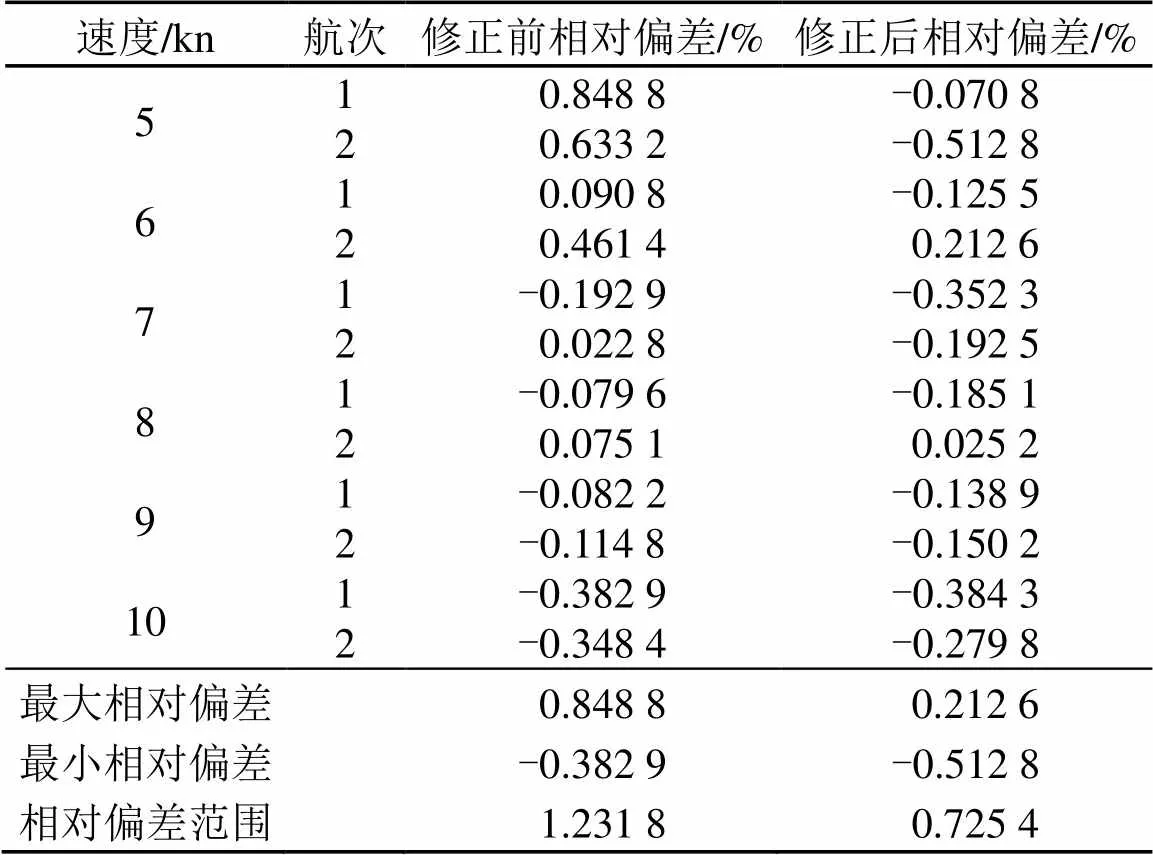
表1 3# ACL测速相对偏差

对其余设备进行同样的处理，结果如表2所示。可以看到，经过该方法处理的测速结果，测速相对偏差都有一定的改善。除了7#设备以外，测速相对偏差范围都控制在1%以内，也即测速相对偏差控制在0.5%以内。

表2 ACL测速相对偏差改善效果

4 结论

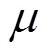
此外，本文讨论了序列二次规划法对速度估计的影响，研究表明，对不同宽度的相关函数，SQP算法均能够较准确地估计目标函数的最大值点，不是产生测速相对偏差的主要原因，即为了减小目标函数最大值点与速度真值的偏差，提高声相关计程仪测速精确度，目标函数的确定是关键。

[1] Jr DICKEY F R, EDWARD J A. Velocity measurement using correlation sonar[C]//Proc. IEEE Plans, San Diego, CA, 1978: 255-264.

[2] KEARY A, HILL M, WHITE P R, et al. Simulation of the correlation velocity log using a computer based acoustic model[C]//11th Int. Symp. Unmanned Untethered Submersible Technol., 1999: 446-454.

[3] ZHU W Q, FENG L, WANG C H, et al. Theory and signal processing of acoustic correlation techniques for velocity measurement of vessel[J]. IEEE J. of Ocean. Eng., 2006, 36(2): 338-346.

[4] DENBIGH P N. Ship velocity determination by Doppler and correlation techniques[C]//IEE Proceedings F-Communications, Radar and Signal Processing, 1984, 131(3): 315-326.

[5] HOLE S K, WOODWARD B, FORSYTHE W. Design constraints and error analysis of the temporal correlation log[J]. IEEE J. of Ocean. Eng., 1992; 17(3): 269-279.

[6] GRIFFITHS G, BRADLEY S E, WATSON G, et al. Acoustic correlation sonar for vertical profiling of ocean currents to a range of 1km[C]//IEE Proeedings-Radar, Sonar and Navigation, 1996; 143(3): 177-183.

[7] 张殿伦, 田坦, 卢逢春. 声相关测速技术仿真与试验研究[J]. 哈尔滨工程大学学报, 2003, 24(4): 415-418.

ZHANG Dianlun, TIAN Tan, LU Fengchun. Simulation and experimental study on acoustical correlation velocity determination technique[J]. Journal of Harbin Engineering University, 2003, 24(4): 415-418.

[8] 冯雷. 相关测速声呐理论、信号处理研究及海试验证[D]. 北京: 中国科学院声学研究所, 2005.

FENG Lei. Theory, signal processing and sea test verification of correlation sonar for velocity measurement[D]. Beijing: Institute of Acoustics, Chinese Academy of Science, 2005.

[9] 蒯多杰. 相关测速声呐系统仿真及处理算法研究[D]. 北京: 中国科学院声学研究所, 2009.

KUAI Duojie. System simulation and algorithm improvements of correlation sonar for velocity measurement[D]. Beijing: Institute of Acoustics, Chinese Academy of Science, 2009.

[10] 易卉芹, 陈龙, 王长红. 相关测速声呐时空相关函数模型改进研究[J]. 声学学报, 2011, 36(5): 484-488.

YI Huiqin, CHEN Long, WANG Changhong. The research of temporal-spatial correlation function model improvement of correlation sonar[J]. Acta Acustica, 2011, 36(5): 484-488.

[11] 王映春, 王长红, 陈龙等. 相关测速声呐阵元坐标估计算法研究[J]. 声学学报, 2013, 38(1): 29-34.

WANG Yingchun, WANG Changhong, CHEN Long, et al. The research of element coordinates estimating algorithm of correlation sonar[J]. Acta Acustica, 2013; 38(1): 29-34.

[12] BOLTRYK P J, HILL M, ALISON C K, et al. Surface fitting for improving the resolution of peak estimation on a sparsely sampled two-dimensional surface with high levels of variance, for an acoustic velocity log[J]. Meas. Sci. Technol., 2004, 15(3): 581-591.

[13] BOLTRYK P J, HILL M, WHITE P R. Improving the resolution of peak estimation on a sparsely sampled surface with high variance using Gaussian processes and radial basis functions[J].Meas. Sci. Technol., 2005, 16(4): 995-965.

[14] ANTHONY L S, JERRY G K, JAMES G H. Method and apparatus for correlation sonar[P]. US: 7295492B2, 2007-11-13.

[15] ANTHONY L S, JERRY G K, JAMES G H. Method and apparatus for fault-tolerant, correlation sonar processing[P]. US: 7738318B2, 2010-06-15.

[16] ANTHONY L S, JAMES G H. Spatial correlation sonar method for high ships speeds[P]. US: 8004934B2, 2011-08-23.

[17] THOMAS V M, SIDNEY I R, STEPHEN M R. Numerical optimization[M]. New York: Springer-Verlag. 2006: 529-561.

[18] ANDREAS A, LU W S. Practical optimization[M]. New York: Springer-Verlag, 2007: 501-529.

[19] SMITH B V, ATKINS P R. Horizontal spatial correlation of bottom reverberation for normal incidence[J].J. Acoust. Soc. Am., 1991, 89(5): 2197-2206.

Accurate velocity estimation of acoustic correlation log based on weighted least squares

YAN Shan-yong1,2, ZHAO Er-liang1,3, QIU Wei1,3, WANG Chang-hong1,3

(1. Ocean Acoustic Technology Center, Institute of Acoustics,Chinese Academy of Sciences, Beijing 100190, China;2. University of Chinese Academy of Sciences, Beijing 100049, China;3. Beijing Engineering Technology Research Center of Ocean Acoustic Equipment, Beijing 100190, China)

An acoustic correlation log utilizes the weighted least square method to determine objective function and the sequential quadratic programming to estimate velocity. The calculation of weights is modified by considering the characteristics of the spatial-temporal correlation of bottom echo. The correlation function and the weight function all have the bell-shaped form. Along with the decrease of the correlation function width or the increase of the distance of the correlation point away from the peak, the mean value of correlation coefficient decreases and its distribution increases, then the weight of the corresponding term of the correlation coefficient in the objective function should also decrease. Under this circumstance, a parameter, which can adjust the width of the weight function, is introduced to enhance the consistency and the accuracy of velocity estimation. The adjustment parameter μ is determined in the calibration of an acoustic correlation log, and different devices may have different adjustment parameters. Trial data has proved the effectiveness of this method in improving the velocity measurement accuracy of different acoustic correlation logs.

acoustic correlation log; weighted least square; sequential quadratic programming; accuracy of velocity measurement

TN911.7

A

1000-3630(2019)-05-0502-06

10.16300/j.cnki.1000-3630.2019.05.004

2018-04-24;

2018-07-11

闫善勇(1990－), 男, 黑龙江哈尔滨人, 博士研究生, 研究方向为水声信号处理。

闫善勇, E-mail: yanshanyongyhy@163.com