基于拓展单位分解有限元法分析声波在多域场内的响应

李鸿秋，姜金辉，陈国平，智淑亚

基于拓展单位分解有限元法分析声波在多域场内的响应

李鸿秋1，姜金辉2，陈国平2，智淑亚1

(1. 金陵科技学院机电工程学院，江苏南京 211169；2. 南京航空航天大学结构力学和控制国家重点实验室，江苏南京 210016)

基于拓展单位分解有限元方法，将平面波函数和贝塞尔函数作为基函数进行拓展。将亥姆霍兹方程离散，求解时不变情况下多域场内声波的响应，并分析基函数对求解精度的影响。将波动方程的时间导数利用二阶中心差分方法离散，得到方程的隐式表达式，划分时间步迭代求解时变情况下声波在多域场内的响应，分析迭代时间间隔对计算精度的影响，与典型算例的精确解进行比较，验证精确性。结果表明，平面波函数作为拓展基函数，利用二阶中心差分法离散时间导数，分析时不变以及时变情况下多域场内高波数声波的响应问题，具有较高的计算精度和计

波动方程；亥姆霍兹方程；单位分解有限元；拓展方法；时变和时不变

0 引言

研究声波的问题归根结底是求解不同边界条件下的波动方程，数值解法大多基于有限元方法[1-2]、有限差分法[3-4]和边界元方法[5-6]。当声波的响应问题涉及到复杂区域，多域场以及高波数等情况时，上述方法就会面临计算量过大或者求解效率较低的问题[7]。尤其对于高波数问题，BUBASKA等[8]的研究表明，即使布置足够多的节点，由于存在污染误差(pollution error)，精度也很难得到保证。近年来，研究者们又发展了谱有限元、边界元方法以及无网格方法计算声波的传播和响应问题[9-11]，但是对于高波数和多域或者复杂域等情况，计算效率和计算精度依然不甚理想。

单位分解有限元方法(Partition of Unity Finite Element Method, PUFEM)能够在现有网格基础上通过附加函数提高计算效率。LAGHROUCHE等[12]的研究表明，PUFEM求解高波数问题时不必细化有限元网格，SHAID等[13]利用高斯函数作为拓展基函数探讨了热场中热的传播问题，并将此方法应用到瞬态热的求解即时域问题。LUOSTARI等[14]应用极弱变分方法，TEZAUR等[15]应用非连续拓展方法以及MONK等[16]利用最小二乘法将单位分解方法应用于边界元方法求解声波和弹性波问题。MOHAMED等[17]分析了上述几种方法的求解局限性和计算效率问题，同时利用平面波作为拓展基函数用于求解不同边界条件下的波动方程，包括多个散射源的问题，取得了不错的计算精度和计算效率。同时，也有其他拓展有限单元方法[18]用于求解波的传播问题，但这些研究往往局限于时间谐波，分析时不变情况下的声波的传播和响应问题。

本文利用四边形等参单元的形函数，采用平面波函数或者贝塞尔函数作为基函数，经拓展建立单位分解有限元的整体形函数。构造求解亥姆霍兹方程整体刚度矩阵。将波动方程的时间导数利用二阶中心差分方法离散，得到波动方程的隐式表达式，求解时变情况下声波在多域场内的响应。

1 声波的响应

1.1 波动方程

声波的传播过程可以描述成波动方程：

1.2 亥姆霍兹方程

波的传播问题都可以归结为在给定的边界条件和初始条件下求波动方程的解。用分离变量的方法求解波动方程，则可以得到不考虑时间问题的亥姆霍兹方程(2)，以及边界条件式(3)。

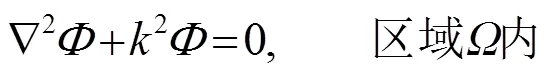
2 拓展单位分解有限元法

拓展单位有限元法的核心思想是由单位分解函数和基函数共同逼近求解空间，基函数不依赖有限元网格，不增加网格，可以通过拓展基函数的阶次提高计算效率和计算精度[19]。基函数的拓展方式可以是均匀的，也可以是不均匀的，不同的基函数有不同的计算精度[20]。

2.1 拓展基函数

从而得到：

将基函数和有限元形函数的乘积看作一个整体，形成新的形函数即：

2.2 误差分析

3 时不变情况下声波在多域场的响应分析

3.1 构造给定边界条件亥姆霍兹方程的积分弱形式

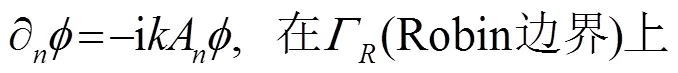
(a) 平面波入射内含圆形边界(Robin边界或Neummn边界)的求解区域

(b) 平面波入射经圆形边界(Neummn边界)反射后的求解区域 图1 求解区域及求解边界示意图 Fig.1 Schematic diagram of the solving models

平面声波入射，，用权重系数分别去乘亥姆霍兹方程式(2)和边界条件式(3)的左右两端，得到：

(10)

(11)

对式(10)应用格林公式得到：

(12)

将式(11)代入式(12)，得到积分弱形式(13)：

(13)

3.2 构造拓展单位分解有限元的整体形函数

采用四边形等参元作为单位分解单元，划分单元(表示单元序号)，求解域为，用平面波函数作为基函数在单位分解单元的节点处进行拓展，拓展个数为个，均匀分布，因此，，其中，。则拓展单位分解有限元的整体形函数可以写成：

(14)

局部节点响应值为： ，则单元内其它点响应值可用式(15)求得：

(15)

3.3 构造时不变情况下拓展单位分解有限元法的刚度矩阵和求解式

设有转换矩阵，使，将各单元自由度按对号入座的方式扩展到整体自由度矩阵，可得下式：

(16)

将式(15)和(16)代入亥姆霍兹方程积分弱形式(13)，得到矩阵形式(17)：

(17)

显然，刚度矩阵为。利用式(17)求。

3.4 数值算例

算例1

如图1(a)所示，入射平面声波为，入射角度为，振幅为单位幅值，求解域为半径为1的圆形区域，其中心位于(1, 1)，域内包含两个半径分别为0.5、圆心位置(0.5, 1.2)和半径为0.25、圆心位置(1.5, 0.5)的圆。入射角度分别为α=0°、30°、60°、90°，波数分别为k=5π、8π、15π、20π。模型的单元个数为60。利用高阶Gauss-Legendre积分方法对式(15)积分。图2~5给出了其中4种情况下的声响应值，表1给出了部分计算结果的误差。

算例2

如图1(a)所示，入射平面波经由满足Neumann边界条件(8b)的圆形表面反射后的响应问题，外截断边界满足Robin边界条件式(8a)。本例中[21]，，其中r、θ分别表示所在位置的极坐标，、分别表示n阶汉克尔函数和贝塞尔函数，、是其对应的微分形式。此算例精确解包含贝塞尔函数，可以采用贝塞尔函数作为基函数，即令。算例2 分别采用平面波函数和贝塞尔函数作为基函数，拓展个数均为8个，计算当入射角度分别为α=0°、60°、90°，波数分别为k=5π、15π、20π，振幅为单位幅值时的声响应值。结果表明，使用平面波函数作为基函数拓展，计算结果优于使用贝塞尔函数作为基函数拓展的情况(见表2)，(a)为基函数为平面波函数时的误差值，(b)为基函数为贝塞尔函数时的误差值。图6~9所示为采用平面波函数为基函数求解得到的声波响应数值。

图2 声波响应势能值的实部(k=8π, α=0°) Fig.2 The real part of the potential energy of acoustic wave response(k=8π, α=0°)

图3 声波响应势能值的实部(k=8π, α=60°) Fig.3 The real part of the potential energy of acoustic wave response(k=8π, α=60°)

图4 声波响应势能值的实部(k=15π, α=90°) Fig.4 The real part of the potential energy of acoustic wave response(k=15π, α=90°)

图5 声波响应势能值的实部(k=20π, α=0°) Fig.5 The real part of the potential energy of acoustic wave response(k=20π, α=0°)

表1 不同波数和入射角情况下的相对误差(算例1) Table 1 The relative errors for different wave numbers and different incident angles (Example 1) kα/(°)εL2 /% 5π02.2570×10-4 5π604.1592×10-4 8π60 2.40×10-2 10π90 1.89×10-2 15π01.5956×10-5 15π901.1530×10-5

表1和表2的误差结果表明，虽然单元网格划分较少，即使单元尺寸已经远远超过了波长，依然能获得较高的计算精度。且当内边界为Neumann边界条件时，精确解包含贝塞尔函数情况下，采用平面波函数作为基函数拓展，同样具有较高的计算精度。

图6 声波响应势能值的实部(k=5π, α=0°) Fig.6 The real part of the potential energy of acoustic wave response(k=5π, α=0°)

图7 声波响应势能值的实部(k=5π, α=60°) Fig.7 The real part of the potential energy of acoustic wave response(k=5π, α=60°)

图8 声波响应势能值的实部(k=10π, α=60°) Fig.8 The real part of the potential energy of acoustic wave response(k=10π, α=60°)

图9 声波响应势能值的实部(k=10π, α=90°) Fig.9 The real part of the potential energy of acoustic wave response(k=10π, α=90°)

表2 不同波数和入射角情况下的相对误差(算例2) Table 2 The relative errors for different wave numbers and different incident angles (Example 2) kα/(°)εL2(a)/%εL2(b)/% 5π02.2570×10-22.67 5π604.1592×10-24.34 10π901.896.54 10π602.715.74

4 时变情况下声波在多域场的响应分析

4.1 构造给定边界条件亥姆霍兹方程的积分弱形式

设声波在空间传播的时间为，域内的波动方程和边界条件可以写成式(1)的形式。则其初始状态为

(18)

时间步长为，表示在时间步时的声响应值。使用隐式方法可以避免显式方法中需要的小时间步长，本文采用二阶中心差分法离散时间导数，迭代公式写成式(19)的形式：

(19)

同样，是在时间步时的响应值。显然，受时间步长和网格划分的影响。同样用权函数w去乘式(19)的两端，并在空间和边界上积分，利用散度定理和边界条件(8a)，得到此类边界条件下波动方程的积分弱形式：

贵州是我国红粘土的主要分布区，红粘土厚度与中国北部的黄土相比厚度较薄，一般厚度为8-10米，局部地区厚度可以达到20多米。厚度的变化主要与下部基岩起伏有关，在岩溶缓坡、盆地等地厚度较大，峰林高地、陡坡等地厚度较薄甚至没有。在红粘土堆积厚的地方有着明显的垂直分带结构，从上到下可分为表土层、全风化层、半风化层和基岩四个结构，而在红粘土堆积较薄的地方垂直分带结构不明显。为了更加详细准确的反映红粘土剖面特征，本次实验选取的8个剖面都发育良好，其中包括贵阳白云岩红粘土剖面两组、石灰岩红粘土剖面一组，安顺白云岩红粘土剖面一组、石灰岩红粘土剖面两组，遵义白云岩红粘土剖面、石灰岩红粘土剖面各一组。

4.2 构造时变情况下拓展单位分解有限元法的刚度矩阵和求解式

在求解域划分单元，求解域表示为，采用平面波函数作为基函数，拓展个数为。同样将式(16)、(17)代入波动方程的积分弱形式(20)，可以得到矩阵求解式：

(21)

式中，。显然，如果能够得到在时间步、时的声响应值和，则可以获得在时间步时的声响应值。

我做梦也想不到李小树会千里迢迢去寻找许春花，可是他真的走了，走的时候，除了给大黑猫带来一些他家里剩余下的猫食外，他还向我讨要许春花的那幅肖像。看到他热切企盼的眼神，我便把画稿送给了他。李小树小心翼翼地把画稿收藏在他事先准备好的一个画筒里，就火急火燎地走了，像阵风似的消失在我的视线里。

4.3 数值算例

算例3

如图1(a)所示，平面波入射，本算例的求解区域为凹字形状的不规则区域，初始条件为：。时变问题解包含时间，其精确解为，分别计算k=5π、10π，α=0°、60°情况下在时间的声响应值。图10、11分别给出了在T时刻的部分结果，相对误差见表3。

图10 声波响应势能值的实部(k=5π, α=0°,T=0.01 s) Fig.10 The real part of the potential energy of acoustic wave response(k=5π, α=0°,T=0.01s)

图11 声波响应势能值的实部(k=5π, α=60°, T=0.005 s) Fig.11 The real part of the potential energy of acoustic wave response(k=5π, α=60°, T=0.005 s)

表3 不同波数,入射角和不同时间步情况下的相对误差(算例3) Table 3 The relative errors for different wavenumbers, different incident angles and different time steps (Example 3) kα/(°)T/sεL2 /% 5π00.0010.001 5 5π00.0020.000 2 10π600.0010.005 6 10π600.0050.004 7

算例4

平面波入射，被圆心为(0, 0)、半径为1的圆形刚性壁反射后的响应，令求解区域是圆心为(4,4)、半径分别为的多域空间。初始条件为：。精确解包含时间项：。

精准医疗是针对于患者医疗保健和健康的个性化医学模式，它通过医生的医疗决策和实践制定出适合不同疾病人群的治疗方案。随着对CRSwNP的发病机制的不断深入了解，精准医疗分析整合疾病的诊断和治疗并能制定出最优化的治疗方案[28]。而实现精准医疗的基础必须具备的要素有：患者参与治疗方案的决定；预判初始治疗的成功率；防治疾病进展的有效策略和疾病内在型为驱动的个性化治疗[29]。为了实现疾病内在型为驱动的治疗目的，必须对疾病的内在型有着充分且标准化的认识，而且能够洞察用于评估或预测疗效、指导完善临床策略的生物标记物[10]。

分别计算k=5π、6π，α=0°、60°情况下的时变响应值，部分结果图见图12和图13所示，相对误差见表4。算例3和算例4的结果显示，利用二阶差分离散时间导数构造整体计算矩阵，基于拓展单位分解有限元法计算时变情况下声波在多域场的响应问题，计算结果精度较高，且当时间步长满足小于1.0×10-3的情况下，如果继续降低时间步长，计算精度变化不大。

图12 声波响应势能值的实部(k=5π, α=0°, T=0.01 s) Fig.12 The real part of the potential energy of acoustic wave response(k=5π, α=0°, T=0.01 s)

图13 声波响应势能值的实部(k=6π, α=60°,T=0.03 s) Fig.13 The real part of the potential energy of acoustic wave response(k=6π, α=60°,T=0.03 s)

表4 不同波数,入射角和不同时间步情况下的相对误差(算例4) Table 4 The relative errors for different wavenumbers, different incident angles and different time steps (Example 4) kα/(°)T/sεL2 /% 5π00.000 10.050 3 5π00.000 20.048 2 6π600.000 10.136 2 6π600.000 30.0125 1

5 结论

基于拓展单位分解有限元方法求解高波数声波在多域场内的响应，分别利用平面波函数，贝塞尔函数作为基函数进行拓展，分析时不变情况下声波在多域场内的响应问题。利用二阶中心差分法离散时间导数，同样基于单位分解有限元法构造波动方程的积分弱形式，用于求解时变情况下声波在多域场内的响应问题，计算结果表明：本文构造的拓展基函数用于波动方程和亥姆霍兹方程的求解计算效率和计算精度较高，并且适用于不规则、多域、复杂区域以及高波数情况下声波响应的求解，此方法对网格的划分数量要求较低，即使网格数量较少，甚至波长大于单元长度依然可以取得较高的计算精度，不增加单位个数通过增加拓展基个数也可以提高计算精度。

参考文献

[1] KOHNO H, BATHE K J, WRIGHT J C. A finite element procedure for multiscale wave equations with application to plasma waves[J]. Computers & Structures, 2010, 88(1-2): 87-94.

[2] HARARI I. A survey of finite element methods for time-harmonic acoustics[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(13): 1594-1607.

[3] PERREY-DEBAINE E, TREVELYAN J, BETTESS P. Wave boundary elements: a theoretical overview presenting applications in scattering of short waves[J]. Engineering Analysis with Boundary Element, 2004, 28(2): 131-141.

[4] HUTTUNEN T, MONK P. The use of plane waves to approximate wave propagation in anisotropic media[J]. Mathematics of Computation, 2007, 204: 350-367.

[5] BUFFA A, HIPTMAIR R, SCHWAB C. Boundary element methods for Maxwell transmission problems in Lipschitz domains[J]. Numerical Mathematics, 2003, 95(3): 459-485.

[6] PERREY-DEBAIN E, TREVELYAN J, BETTESS P. Wave boundary elements: a theoretical overview presenting applications in scattering of short waves[J]. Engineering Analysis with Boundary Elements, 2004, 28(2): 131-41.

[7] GUDDATI M N, YUE B. Modified integration rules for reducing dispersion error in finite element methods[J]. Computational Methods in Applied Mathematics, 2004, 193(3-5): 275-287.

[8] BABUSKA I M, SAUTER S A. Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers[J] SIAM REVIEW, 2000, 42(3): 451-484.

[9] CHAKRABORTY A, GOPALAKRISHNAN S. A spectral finite element model for wave propagation analysis in laminated composite plate[J]. Journal of Vibration and Acoustics, 2006, 128(4): 477-488.

[10] HAM S, LAI B, BATHE K J. The method of finite spheres for wave propagation problems[J]. Computers and Structures, 2014, 142: 1-14.

[11] GENECHTEN B, VANDEPITTE D DESMET W. A trefftz-bassed numerical modelling framework for Helmholtz problems with complex multiple scatter configurations[C]//Proceedings of the ICCES Special Symposium on Meshless & Other Novel Computational Methods; 2008, Suzhou, China.

[12] LAGHROUCHE O, BETTESS P, PERREY-DEBAIN E, et al. Wave interpolation finite elements for Helmholtz problems with jumps in the wave speed[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(2): 367-381.

[13] MOHAMED S, MOHAMMED S, TREVELYAN J. A partition of unity FEM for time-dependent diffusion problems using multiple enrichment functions[J]. International Journal for Numberical Mehtods in Engineering, 2013, 93(3): 245-265.

[14] LUOSTARI T, HUTTUNEN T, MONK P. The ultra weak variational formulation using Bessel basis functions[J]. Communications in Computational Physics, 2012, 11(2): 400-414.

[15] TEZAUR R, KALASHNIKOVA I, FARHAT C. The discontinuous enrichment method for medium-frequency Helmholtz problems with a spatially variable wavenumber[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 268(1): 126-140.

[16] MONK P, WANG D Q. A least-squares method for the Helmholtz equation[J]. Communications in Numerical Methods in Engineering, 1999, 175(1): 121-136.

[17] MOHAMED M S, MOHAMMED S, LAGHROUCHE O. An enriched finite element model with q-refinement for radiative boundary layers in glass cooling[J]. Journal of Computational Physics, 2014, 258: 718-737.

[18] VERGOT K, VANMAELE C, VANDEPITTE D. An efficient wave based approach for the tiem-harmonic vibration analysis of 3d plate assembly[J]. Journal of Sound and Virbration, 2013, 332(8): 1930-1946.

[19] CHRISTODOULOU K, LAGHROUCHE O, MOHAMED M S. High-order finite element for the solution of Helmholtz problems[J]. Computers and Structures, 2017, 191: 129-139.

[20] MOHAMED M S, LAGHROUCHE O, EL-KACIMI A. Some numerical aspects of the PUFEM for efficient solution of 2D Helmholtz problems[J]. Computers and Structures, 2010, 88(2): 1484-1491.

[21] LINTON C M, EVANS D V. The interaction of waves with arrays of vertical circular cylinders[J]. Journal of Fluid Mechanics, 1990, 215(1): 549-569.

Analysis of acoustic wave response in complex multiple domains based on the enriched partition of unit finite element method

LI Hong-qiu1, JIANG Jin-hui2, CHEN Guo-ping2, ZHI Shu-ya1

(1. College of Mechanical and Electrical Engineering, Jinling Institute of Technology, Nanjing 211169, Jiangsu, China; 2. State Key Laboratory ofMechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, Jiangsu, China)

Abstract: Based on the enriched partition of unity finite element method, the plane wave functions or Bessel functions are enriched as basis functions to discretize Helmholtz equation, the response of acoustic wave in complex multiple domains under time-independent condition is solved and the effect of basis functions on solution accuracy is analyzed. The two-order central difference method is used to discrete time derivative of the wave equation for implicit solution and the time step iterative method is used to solve the response of acoustic wave in complex multiple domains under time-dependent condition. By taking the plane wave function enriched as basis function and using the two-order central difference method to discrete time derivative, the responses of high wavenumber acoustic waves in complex multiple domains under time-dependent and time-independent conditions are calculated. Also, the effect of iterative time interval on calculation accuracy is analyzed. Typical examples are used to compare the calculation results with the exact solutions and to verify the method in this paper having high accuracy and efficiency.

Key words: wave equation; Helmholtz equation; partition of unity finite element;enriched method; time-dependent and time-independent

算效率。

中图分类号：O429

文献标识码：A

文章编号：1000-3630(2019)-05-0481-07

DOI编码：10.16300/j.cnki.1000-3630.2019.05.001

收稿日期: 2018-05-03;

修回日期: 2018-06-18

基金项目: 江苏省自然科学基金资助(BK20151099)；金陵科技学院科研基金资助(JIT-B-201219)；江苏省高校优秀中青年教师和校长境外研修计划资助

作者简介:李鸿秋(1973－), 女, 河北邯郸人, 博士研究生, 副教授, 研究方向为振动与噪声控制。

通讯作者: 李鸿秋,E-mail: lihongqiu@jit.edu.cn