基于波束计算的水下声学探测设备声兼容传播过程分析

冯雪磊，葛锡云，周宏坤，魏柠阳

基于波束计算的水下声学探测设备声兼容传播过程分析

冯雪磊，葛锡云，周宏坤，魏柠阳

(中国船舶科学研究中心深海载人装备国家重点实验室，江苏无锡 214082)

对于搭载多种声学探测设备的水下平台，不同设备的信号可能会产生相互干扰。因此，根据探测设备的波束特性，针对水下平台对海底的探测情形，来分析探测设备声兼容传播过程的特性。结合射线声学和海底散射模型，建立了声兼容分析中声传播的计算方法，并且分析了传播过程中各种因素对声兼容设计的影响。结果表明，在算例的波束条件下，声速剖面对声兼容性的影响较小，而特定类型的海底底质的影响较大。此外，水下平台距海底越高，或者波束偏转越大，声学设备间的相互干扰就越大。为了尽可能减小干扰信号的影响，应尽量避免干扰信号的发射波束和接收波束交叠，此外还给出了波束覆盖角阈值和干扰信号衰减的关系。

波束计算；声兼容；射线声学；海底散射

0 引言

随着国内外非传统潜艇技术的发展[1]，以探测作业为主要使命任务的深海水下平台受到越来越多的关注。这一类水下作业平台通常搭载大量的水下声学设备，以实现探测、通信、导航、定位等功能[2]。对于水下声学探测设备，不同类型的设备为了实现相对一致的探测范围，通常选择较为接近的工作频段。当这些设备同时工作时，多个设备的目标回波信号可能会交叠在一起，造成设备的相互干扰。这就需要在水下平台设计阶段，预先考虑各个设备的声学兼容性，充分发挥水下声学探测设备的效能。

对于水下声学设备间的相互干扰和声兼容，目前已经开展了很多研究。抑制声学设备相互干扰的方法主要可以分为频分法、时分法、波分法和空间分置法。频分法就是为声学设备划分不同的工作频率，然而由于换能器的非线性失真，工作在不同频率的设备仍然可能相互干扰，此外不同频率的强干扰还可能造成信号的饱和失真[3]。时分法是搭载多型声学探测设备的水下平台的常用抗干扰方法，但是这种方法以牺牲探测效率为代价，并且可能会降低沿航迹方向的分辨率。波分法可以有效提高声学设备的抗干扰能力，是目前的研究热点[4-7]，但是这需要预先协调各个设备的波形和处理算法，对于采用定型设备或者现有设备的探测系统较难实现。空间分置法尽量避免不同设备波束之间的交叠，可以简单有效地避免干扰[8]。空间分置法较难在小型平台上实现，但是随着大型深海平台的研制，空间分置法有望成为抗干扰的有效手段。

声学设备的声兼容分析非常复杂，涉及声波的发射、传播和接收，受到设备本身的影响以及传播环境的影响。本文基于波束计算，对深海平台水下探测设备的声兼容进行分析，主要针对声传播过程，分析波束和环境因素的相对影响，为声兼容的研究和设计工作提供参考。

1 波束计算方法

以深海水下平台的声学探测设备为背景，假定声学探测设备安装在水下平台的底部，探测海底地形地貌等信息。某一声学设备发射的声信号为干扰源，对另一声学设备产生干扰。对探测而言，多个声学设备同时工作同步发射声波时，声学设备主要受到其他设备海底回波的干扰，因此考虑：某一声学设备的发射基阵发出的干扰信号经海底散射后被另一声学设备的接收基阵所接收的情形。由于探测海底地形地貌的声学设备采用高频声信号，因此声传播计算方法采用声线追踪法，此外海底散射采用双基地Jackson模型[9]。由于水下平台工作在深海，且换能器基阵安装在水下平台的底部，因此忽略水面反射。

1.1 声线追踪

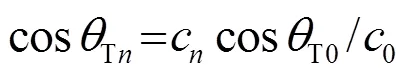
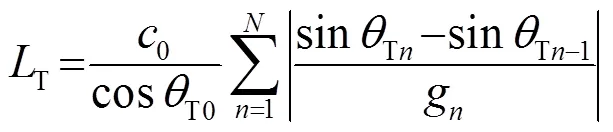
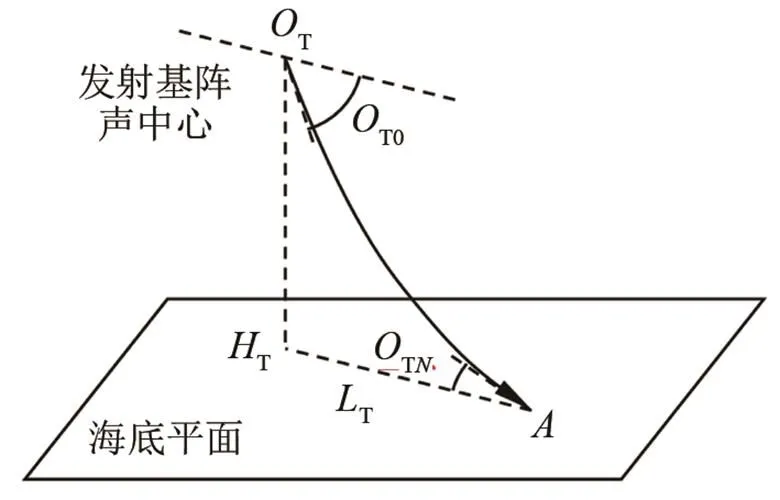
(a) 发射声线

(b) 第个水层

图1 声线追踪示意图

Fig.1 Schematic diagram of acoustic ray tracing

1.2 海底散射

为求得发射基阵发射的声波经海底散射后被接收基阵接收的总声强，可以将海底划分为若干个面元，这样接收基阵接收到的总声强，是海底所有面元的散射声强的求和。

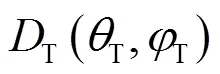
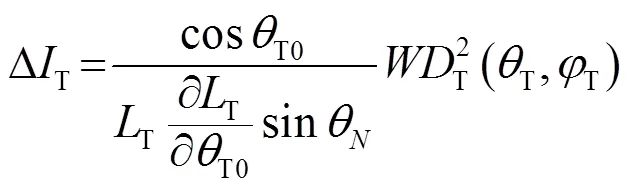
将式(1)代入式(2)，并经过计算和化简可得：

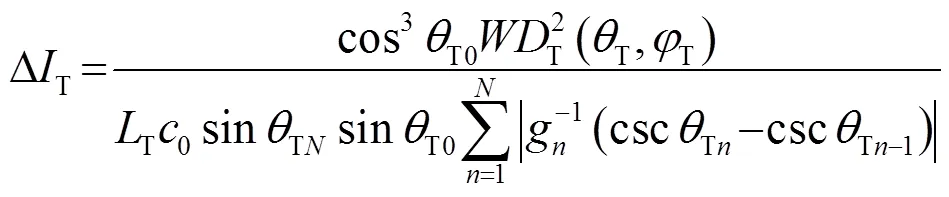
根据射线声学理论，第个海底面元接收到的声能为

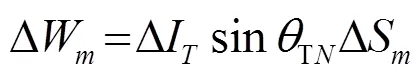
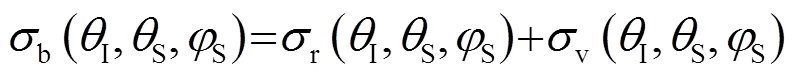
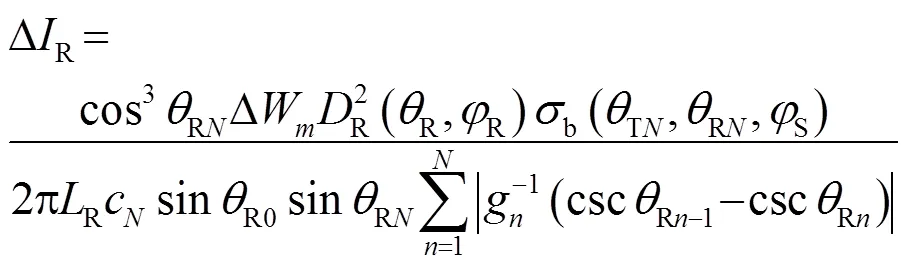
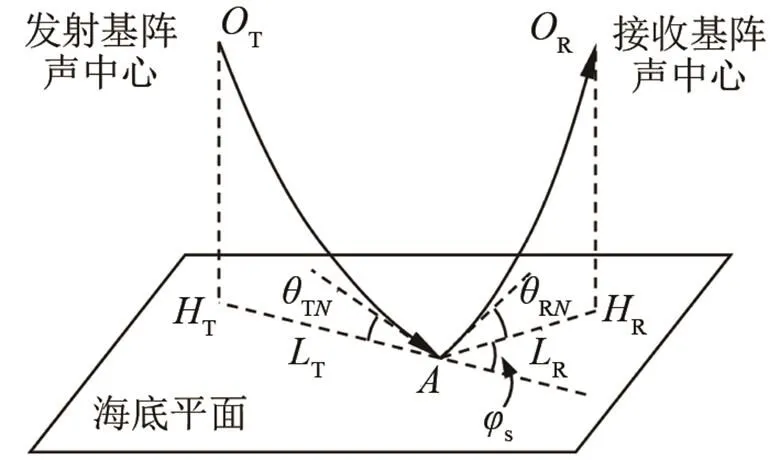
图2 海底散射示意图

综合式(3)～(6)可得经海底散射后接收基阵接收到的总声强为

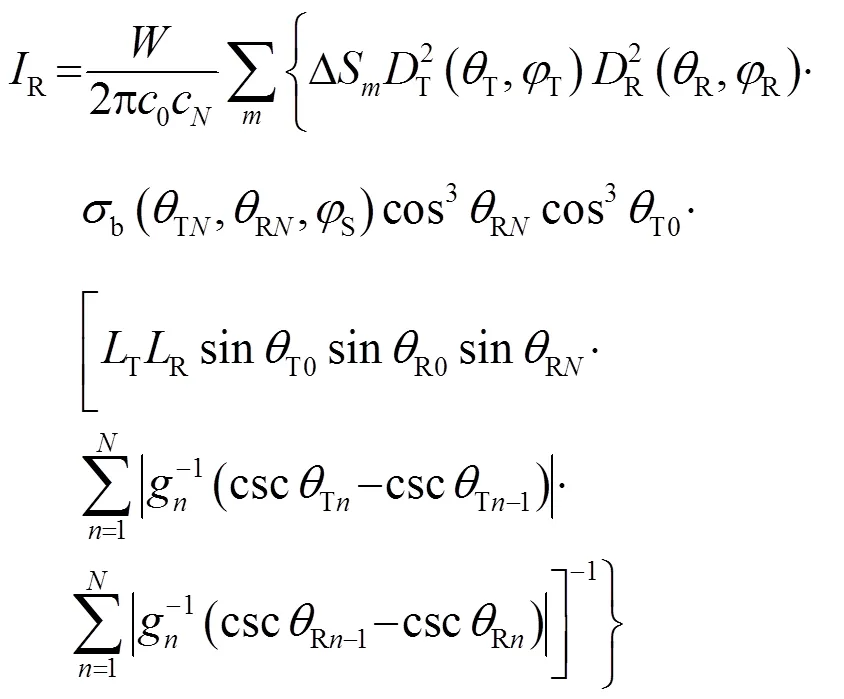
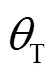
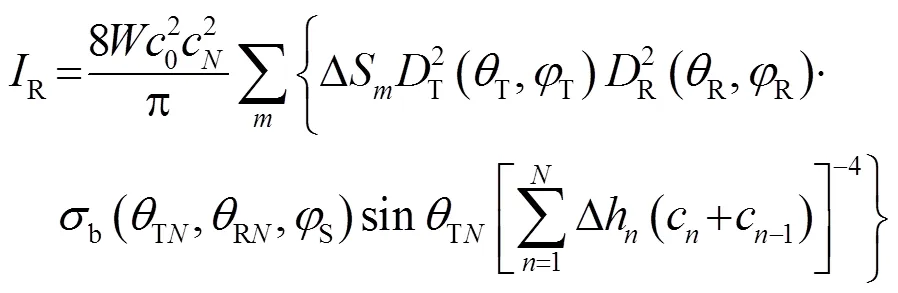
2 计算设定

2.1 波束设定

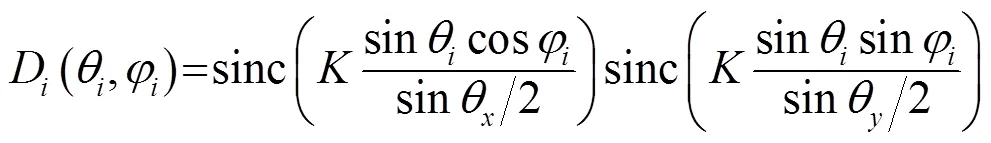
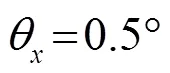
2.2 环境参数设定

海水声速剖面数据参照某海域1 000 m深度的相关数据[10]，除非另有说明，水下平台工作深度处的声速取为1 486 m·s-1，假定水下平台距海底200 m，海底附近的声速取为1 490 m·s-1，从水下平台到海底的声速按照正恒梯度线性变化。参照声呐的相关参数，工作频率取为100 kHz。

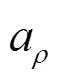
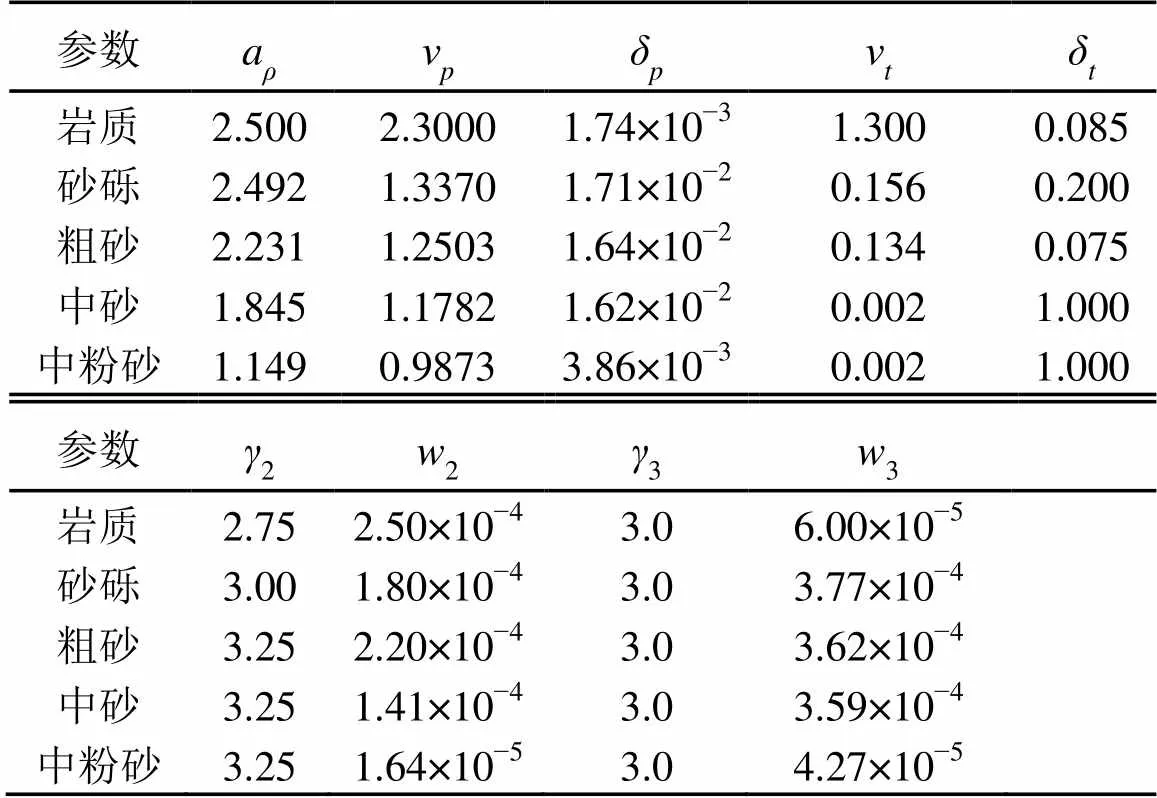
表1 海底散射模型中的底质参数

3 结果与分析

为了研究空间分置法的抗干扰能力，计算发射基阵和接收基阵不同间距时的干扰信号强度。由于干扰信号强度与声源级等参数有关，因此计算相对于发射基阵和接收基阵间距为0时(即收发合置)的干扰信号的衰减量。考虑到水下平台的底部通常为沿艏艉方向的狭长形，发射基阵和接收基阵在左右舷方向可以分置的间距非常有限，因此假定发射基阵和接收基阵左右舷方向的间距为0，而计算艏艉方向不同间距的干扰信号衰减。此外，除非另有说明，以下分析中的参数参见2.2节。

3.1 声速剖面的影响

不同声速剖面情况下干扰信号衰减随基阵间距的变化如图3所示，其中正梯度声速剖面为默认声速剖面，即声速从水下平台工作深度处的1 486 m·s-1线性变化到海底附近的1 490 m·s-1；恒定声速剖面是声速固定为1 486 m·s-1，不随深度变化；负梯度声速剖面参考浅海情形，声速从水下平台工作深度处的1 525 m·s-1线性变化到海底附近的1 500 m·s-1。由图3可见，干扰信号衰减曲线在不同声速剖面条件下变化不大。这主要是由于发射波束和接收波束的交叠部分角度较小，在本例中交叠部分约为0.6°×1.1°，因此从不同角度发射的声线相差较小，波束交叠部分在海底的“脚印”的形状随声速剖面变化不大。

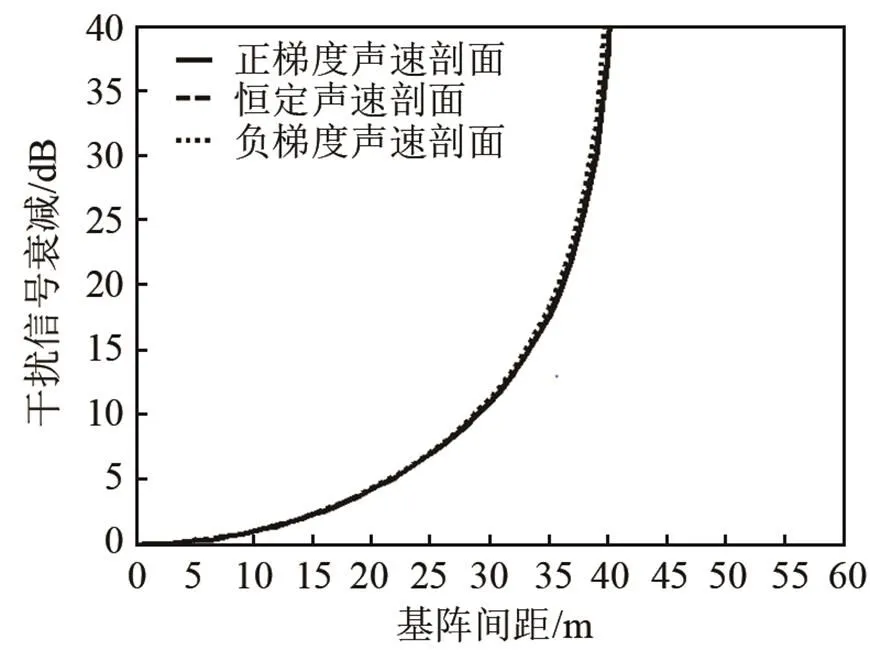
图3 不同声速剖面情况下干扰信号衰减随基阵间距的变化

3.2 海底底质的影响

图4为不同海底底质情况下干扰信号衰减随基阵间距的变化，其中各种海底底质的参数如表1所示。海底底质可以分为三类[9]：第一类底质的粗糙度较大，并且剪切效应较强，如“岩质”、“砂砾”等；第二类底质的粗糙度中等，剪切效应较小，底质的压缩波声速比海水声速大，如“粗砂”、“中砂”等；第三类底质的粗糙度和剪切效应可以忽略，底质的压缩波声速比海水声速小，如“中粉砂”等。由图4可知，第一类和第二类底质对干扰信号衰减曲线的影响较小，而第三类底质对干扰信号衰减曲线的影响较大。这主要是由于波束交叠区域的海底入射掠射角和散射掠射角约为90°，第一类和第二类底质在这一角度条件下的散射强度变化不大，而第三类底质这一角度条件下的散射强度变化较大。在第三类底质条件下，空间分置法得到的干扰信号衰减要大于其他类型的底质。

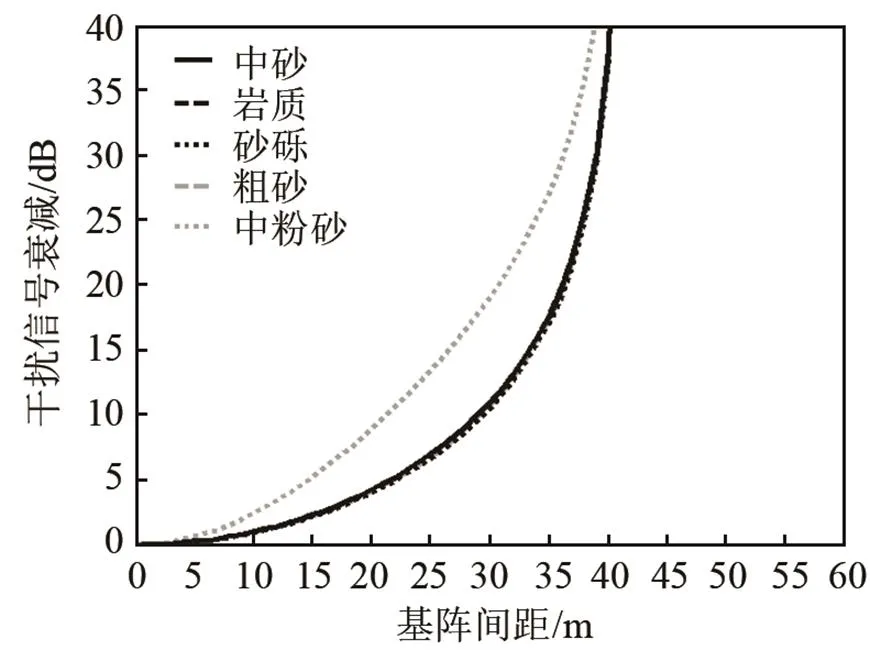
图4 不同海底底质情况下干扰信号衰减随基阵间距的变化

3.3 距底高度的影响

图5为不同距底高度情况下干扰信号衰减随基阵间距的变化。由图5可见，距底高度越高，干扰信号衰减越小。这是显见的，由于波束开角不变，距离海底越远，波束交叠部分在海底的“脚印”越大，于是基阵间距的影响就越小。这提示距底高度越大，越不利于声学抗干扰。然而换能器基阵距底高度越大，海底散射回波越微弱，因此上述分析仅针对海底回波足够强，以至于能产生干扰的情形。

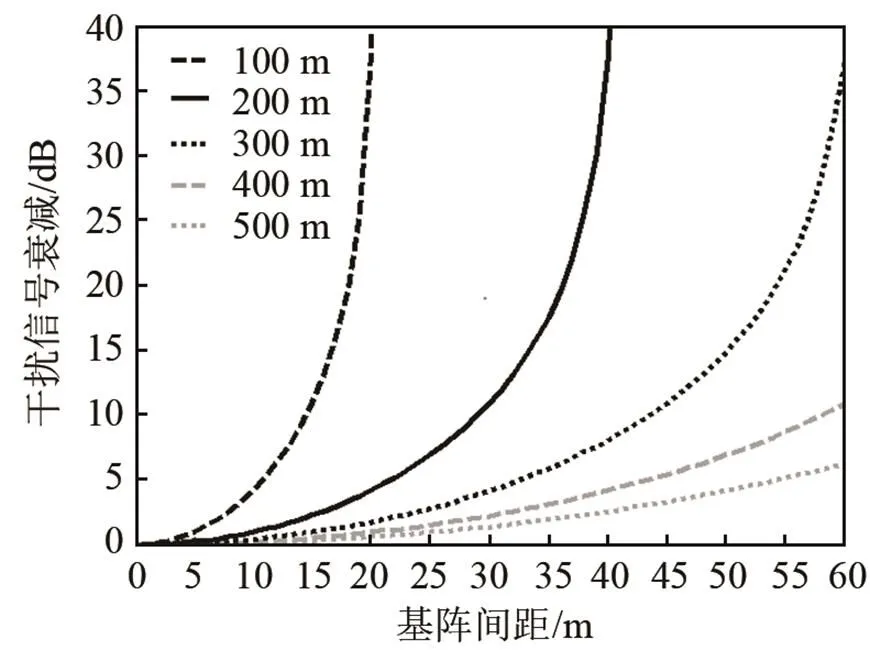
图5 不同距底高度情况下干扰信号衰减随基阵间距的变化

3.4 偏转角度的影响

部分声学探测设备可以通过相控阵技术使波束偏转，以对左右舷方向的海底条带进行扫描。波束可以向艏艉方向偏转，也可以向左右舷方向偏转。向艏艉方向偏转和增大基阵间距的分析是类似的，因此不再讨论。不同偏转角度情况下干扰信号衰减随基阵间距的变化如图6所示，考虑到水下平台通常是对称的，因此不妨假定向左舷方向偏转，这里的偏转角度是指波束主轴方向与垂直方向的夹角。由图6可见，从整体趋势而言，偏转角度越大，干扰信号衰减越小。这提示波束偏转越大，越不利于声学抗干扰。这主要是由于偏转角度越大，换能器基阵距波束在海底的“脚印”越远，海底“脚印”越大。此外观察发现，在不同偏转角度情况下，干扰信号曲线的变化趋势有所不同，这主要是由于波束偏转，海底入射掠射角和散射掠射角在不同的角度附近变化，对应的海底散射强度的变化趋势不尽相同。

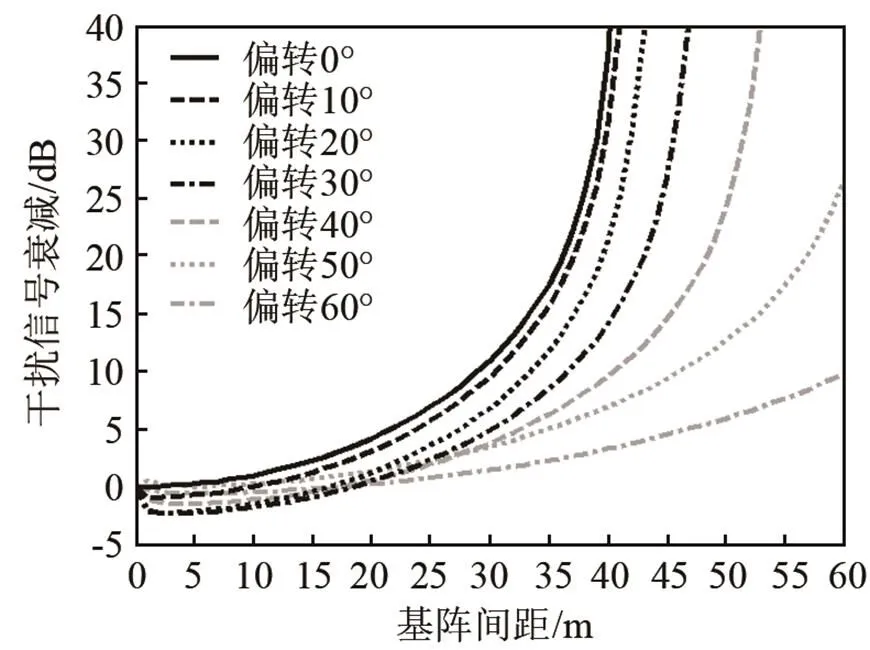
图6 不同偏转角度情况下干扰信号衰减随基阵间距的变化

3.5 旁瓣的影响

波束旁瓣可能会对声学探测设备的性能产生负面影响，因此以基阵自然产生的旁瓣为例，计算旁瓣的影响，如图7所示。根据式(9)，一级旁瓣为−13.3 dB，二级旁瓣为−17.8 dB。由图7可见，当基阵相距较近时，旁瓣的影响不大，只略微增加干扰信号强度，这是由于旁瓣相对于主瓣能量较小。而当基阵相距较大时，旁瓣会显著提高干扰信号强度，这是由于此时波束交叠部分主要为旁瓣部分。相对而言，接收波束旁瓣的影响比发射波束旁瓣的影响大得多，这是由于基阵间距是在艏艉方向变化，在这一方向接收波束的宽度为10°，远大于发射波束宽度0.5°。

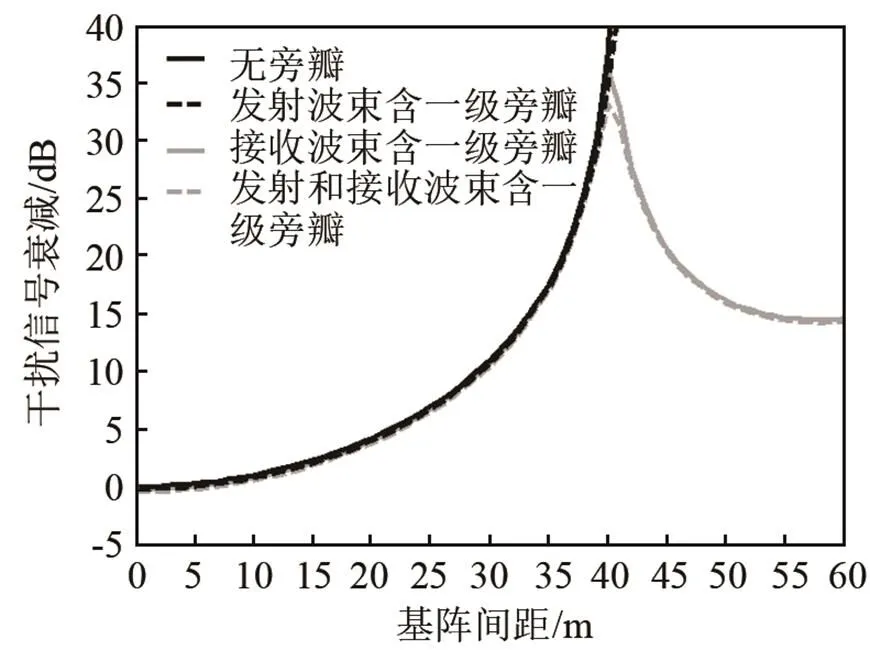
(a) 一级旁瓣的影响

(b) 二级旁瓣的影响

图7 波束旁瓣对干扰信号衰减随基阵间距的变化的影响

Fig.7 The effects of beam sidelobes on the variation of interfer- ence signal attenuation with distance between arrays

3.6 收发波束交叠程度的影响

通常规定波束主瓣周围声压级比主瓣最大声压级低3 dB或6 dB之间的立体角为波束覆盖角，即波束覆盖角的阈值为−3 dB或者−6 dB，不同的阈值对应不同的覆盖角和波束在海底的“脚印”。干扰信号强度主要受到波束交叠部分的影响，为了定量研究干扰信号强度和波束交叠程度的关系，本文计算发射和接收波束主瓣在海底的“脚印”外切时的干扰信号衰减量。这里采用不同阈值情况下发射和接收波束主瓣在海底的“脚印”外切来表征波束交叠的程度，若阈值取为0，则发射和接收波束主瓣最大程度交叠，若阈值取为−∞，则发射和接收波束主瓣完全不交叠。不难发现，选择的阈值越小，覆盖角的范围越大，发射波束和接收波束在海底的“脚印”外切对应的基阵间距越大。

图8所示为选择不同的波束覆盖角阈值对应的干扰信号衰减量，考虑到距底高度和波束偏转对干扰信号的影响较大，因此要计算这些因素的影响。由图8可见，在各种条件下，波束覆盖角阈值和干扰信号衰减的关系都大致相同。进一步的计算表明，为使干扰信号至少衰减3 dB，应使波束覆盖角阈值约−2.6 dB对应的波束不交叠；为使干扰信号至少衰减6 dB，应使波束覆盖角阈值约为−5.2 dB对应的波束不交叠；为使干扰信号至少衰减10 dB，应使波束覆盖角阈值约为−8.5 dB对应的波束不交叠；为使干扰信号至少衰减20 dB，应使波束覆盖角阈值约为−16.2 dB对应的波束不交叠。

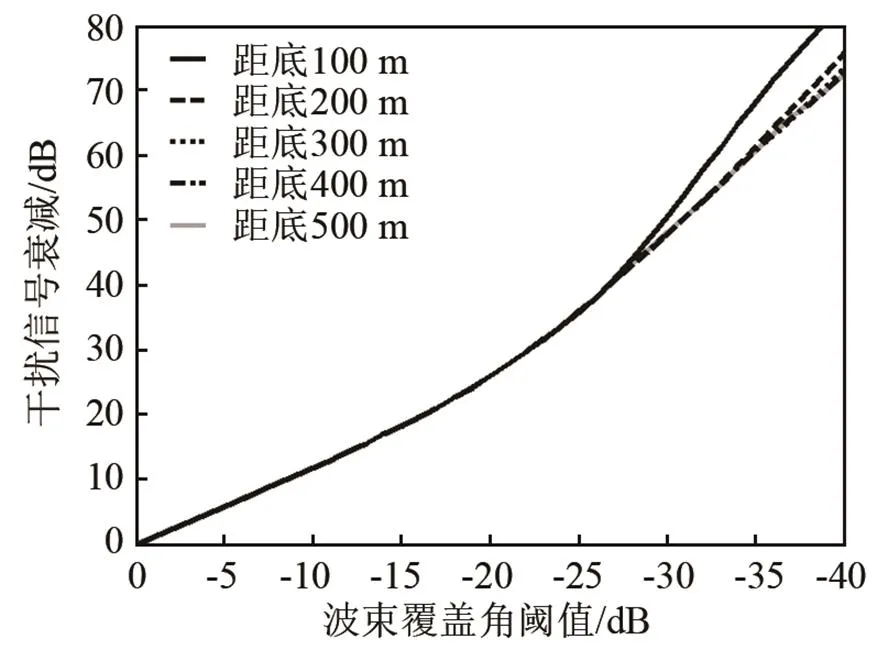
(a) 不同距底高度

(b) 不同偏转角度

图8 波束不交叠时干扰信号的最小衰减量随波束边缘的变化

Fig.8 Variation of the minimum interference signal attenuation with beam edge when no overlapping occurs between beams

4 结论

结合射线声学和海底散射模型，推导了水下平台搭载的声兼容分析中声传播的计算方法，并根据发射基阵和接收基阵的典型波束特性，计算了多种情况下的干扰信号特性。结果表明，对于频率相近的声学探测设备：(1) 对于发射波束和接收波束交叠较窄的情形，缓变声速剖面对干扰信号的影响较小；(2) 相对于其他海底底质，工作在压缩波声速小于海水声速的底质条件时相互干扰较低；(3) 距海底高度越大或者波束偏转越大，声学设备间的相互干扰越大；(4) 基阵间距较小时波束旁瓣的影响较小，而基阵间距较大时波束旁瓣的影响较大。为了尽可能衰减干扰信号，应尽量避免干扰源发射波束和接收波束交叠。

声学兼容设计除了需要考虑信号的强度以外，还需进一步考虑信号的时域和频域特性，以及各种声学探测设备的信号解算方法，将这一系列因素融合到声学兼容性算法是后续的研究方向。此外，声学兼容设计的效果也需要后续进行实验来进一步验证。

[1] 彭亮斌, 吴有生, 司马灿, 等. 国外非传统艇型及结构潜艇技术发展与总体设计思想分析 [J]. 船舶力学, 2017, 21(7): 914-928.

PENG Liangbin, WU Yousheng, SIMA Can, et al. Investigation on technical development status and general design ideas for non-body of revolution and new-type structure submarines[J]. Journal of Ship Mechanics, 2017, 21(7): 914-928.

[2] 朱敏, 张同伟, 杨波, 等. 蛟龙号载人潜水器声学系统[J]. 科学通报, 2014, 59(35): 3462-3470.

ZHU Min, ZHANG Tongwei, YANG Bo, et al. Sonar system of Jiaolong human-occupied vehicle[J]. Chinese Science Bulletin, 2014; 59(35): 3462-3470.

[3] 胡晓宇, 张森, 唐劲松. 主动声纳抗同频干扰技术研究[J]. 舰船电子工程, 2008, 28(12): 65-67.

HU Xiaoyu, ZHANG Sen, TANG Jinsong. Study on suppressing in-line jamming for active sonar[J]. Ship Electronic Engineering, 2008, 28(12): 65-67.

[4] 姜可宇. 水声系统主动声纳之间声兼容性理论分析与建模[J]. 声学技术, 2016, 35(6 Pt. 2): 274-276.

JIANG Keyu. Underwater acoustic compatibility analysis and modeling among active SONAR [J]. Technical Acoustics, 2016, 35(6 Pt. 2): 274-276.

[5] 刘贯领, 沈文苗, 凌国民. 声纳信号抗混响能力和声兼容性分析 [J]. 声学技术, 2008, 27(3): 319-322.

LIU Guanling, SHEN Wenmiao, LING Guomin. Analysis of sonar waveform reverberation suppression and acoustic compatible capabilities[J]. Technical Acoustics, 2008, 27(3): 319-322.

[6] 武岩波, 朱敏, 张琳园, 李欣国, 等. 4500米载人潜水器水声通信系统——调制方式及兼容设计[J]. 声学技术, 2015, 34(6 Pt. 2): 244-247.

WU Yanbo, ZHU Min, ZHANG Linyuan, LI Xinguo, et al. Underwater acoustic communication system for 4500m manned submersible: modulation methods and design consideration[J]. Technical Acoustics, 2015, 34(6 Pt. 2): 244-247.

[7] 刘贯领, 沈文苗. 一个解决声呐系统同频干扰的新思路[J]. 应用声学, 2009, 28(2): 97-102.

LIU Guanling, SHEN Wenmiao. A novel method to cope with the acoustic compatibility problem[J]. Applied Acoustics, 2009, 28(2): 97-102.

[8] 张卫, 吴波. 利用非技术手段提高水声兼容效能的研究[J]. 舰船电子工程, 2008, 28(10): 166-169.

ZHANG Wei, WU Bo. Research on improving the effectiveness of underwater acoustic compatibility based on non-technical method[J]. Ship Electronic Engineering, 2008, 28(10): 166-169.

[9] JACKSON D R. High-Frequency Bistatic Scattering Model for Elastic Seafloors[R]. 2000, USA: Applied Physics Laboratory University of Washington, APL-UWTM 2-00.

[10] 刘伯胜, 雷家煜. 水声学原理 [M]. 哈尔滨: 哈尔滨工程大学出版社, 1993.

LIU Bosheng, LEI Jiayu. Principle of underwater acoustics[M]. Harbin: Harbin Engineering University Press, 1993.

[11] DRUMHELLER D M, GRAGG R F. Evaluation of a fundamental integral in rough-surface scattering theory[J]. J. Acoust. Soc. Am., 2001, 110(5): 2270-2275.

Analysis of acoustic compatibility for underwater acoustic survey devices by beam computation

FENG Xue-lei, GE Xi-yun, ZHOU Hong-kun, WEI Ning-yang

(State Key Laboratory of Deep-Sea Manned Vehicles, China Ship Scientific Research Center, Wuxi 214082, Jiangsu, China)

For the underwater platform with mutiple acoustic survey devices, the signals of different devices may interfere with each other. The anti-interference performance of space separation method is therefore analyzed based on the beam patterns of acoustic survey devices in seafloor survey. The acoustic compatibility algorithm is established by combining ray acoustics and high-frequency bistatic scattering model for elastic seafloors. The influences of multiple factors on acoustic compatibility design are analyzed. The results indicate that for the beam pattern of the calculation example, the sound velocity profile is a minor factor, while for specific types of seafloor it is a major factor. If the distance between underwater platform and seafloor is larger or the beam deflection is larger, the design of acoustic compatibility will be more difficult. In order to minimize the impact of interference signals, the transmitting beam and receiving beam of the interference signal should be avoided to overlap as far as possible. In addition, the relationship between the beam coverage threshold and the interference signal attenuation is given.

beam computation; acoustic compatibility; ray acoustics; seafloor scattering

TB566

A

1000-3630(2019)-05-0495-07

10.16300/j.cnki.1000-3630.2019.05.003

2018-06-07;

2018-08-18

国家自然科学基金项目(11904330)、国家重点研发计划项目(2017YFB0202701)资助。

冯雪磊(1989－), 男, 江苏无锡人, 博士, 工程师, 研究方向为声学探测。

冯雪磊,E-mail: xlfeng@hotmail.com