多缺陷兰姆波拓扑成像

张海燕，李加林，徐梦云

多缺陷兰姆波拓扑成像

张海燕，李加林，徐梦云

(上海大学，上海 200444)

将时间反转理论与拓扑优化思想结合在一起，引入了直接声场和伴随声场的概念。通过将时间反转后的兰姆波散射信号作为伴随声场中的二次激励源，实现了信号在缺陷处的聚焦，并根据时域拓扑能量公式计算出检测区域内各点的拓扑能量值，从而对薄板内多缺陷进行表征。有限元仿真和实验表明：在多缺陷情形下，延迟叠加法(Delay and Sum, DAS)因受瑞利准则的约束而在缺陷间距小于分辨率阈值时，无法对缺陷位置进行定位；时域拓扑能量法通过兰姆波时间反转聚焦、图像融合，不仅提高了缺陷检测分辨率，还消除了多模式、有噪声环境下伪像的干扰。有效推动了兰姆波在板类结构无损检测中的应用。

时域拓扑能量；分辨率；兰姆波

0 引言

随着现代科技的迅速发展，常规的超声体波无损检测方案已经无法满足现在工业发展的需求。相比于超声体波，兰姆波[1]具有传播距离远、衰减小、效率高等优点。目前常用的延迟叠加无损检测方法，由于受到瑞利准则[2]的约束，在多缺陷情形下，成像分辨率较差。SYNNEVAG等[3]将延迟叠加波束成形算法与自适应算法相结合，在一定程度上改善了医疗无损检测图像的质量，但分辨率依然还有很大的提升空间。

近些年来，研究人员已从理论、算法等方面对拓扑成像做了大量的研究。拓扑梯度最早出现在机械结构优化中，GUZINA等[4]首次将拓扑梯度应用于超声逆散射成像，并对成本函数的渐近过程，以及拓扑灵敏度的提高等进行了介绍。尽管拓扑渐近可以对缺陷精确定位，甚至可以反演出缺陷的类型，然而，拓扑渐近过程需经过多次迭代，这就不得不考虑计算复杂度的问题。2010年，DOMINGUEZ等[5]提出了拓扑能量法，该方法尽管检测精度不及拓扑梯度法，但却在很大程度上缩短了成像所需的时间，因而更适合于实际应用。

本文基于延迟叠加算法、时域拓扑能量法的检测原理，在多缺陷情形下，分别进行了有限元仿真和实验，并根据成像结果，重点从检测分辨率的角度对两种方法进行了对比分析。

1 延迟叠加算法

1.1 延迟叠加算法原理

1.2 延时计算

线性阵列是一种常用的阵列类型，其通常由多个一定长度的阵元构成，为了便于研究，可忽略阵元的形状，将其理想化为一系列的点声源[8]。对于元等间距排列的线性阵列而言，假设阵元中心之间的间距为，若以线性阵列的中心作为原点，则可建立如图1所示的坐标系。

图1 线性阵元收发示意图

阵元的位置为

2 时域拓扑能量算法

2.1 时域拓扑能量算法原理

(a) 参考试块

(b) 待测试块

图2 试块模型俯视图

Fig.2 Top view of sample model

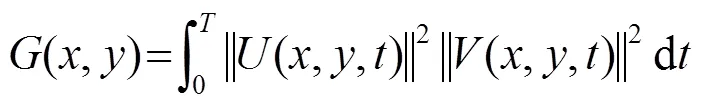
其中，为信号的截止时间，点(,)为成像区域的坐标。

2.2 声场计算

在伴随声场的计算过程中不需要对散射信号做时间窗口截取。由兰姆波的传播模型同样可以得到参考试块中的伴随声场为

3 仿真与实验

3.1 仿真与结果

本文中采用Pzflex仿真软件建立铝板有限元模型，具体参数如表1所示。

表1 有限元仿真模型参数表

有限元仿真中待测试块模型如图3所示，两个圆形通孔缺陷的半径均为5 mm，坐标原点1位于两缺陷圆心连线的中点上。在模型1中，缺陷间距=48 mm；模型2中，缺陷间距=18 mm。

图3 待测试块仿真模型俯视图

本文采用汉宁窗调制的5个周期正弦信号作为激励信号，中心频率为500 kHz，采用反对称激励方式。由兰姆波的频散特性可知，在频厚积为1 MHz·mm时，上下对称激励产生的兰姆波为模式，在速度=5 200 m·s-1，中心频率为500 kHz时，对应的波长=10.4 mm。

3.1.1 延迟叠加算法仿真结果

图4 第11个传感器接收到的散射信号波形

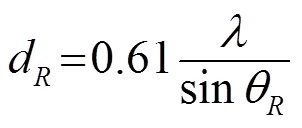
(a) 缺陷间距1=48 mm

(b) 缺陷间距2=18 mm

图5 不同缺陷间距下的DAS成像结果

Fig.5 DAS imaging results for different defect spacing

3.1.2 时域拓扑能量仿真结果

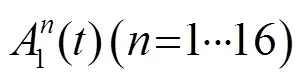
(a) 所有阵元接收到的散射信号

(b) 时间反转后的散射信号

(c) 到达缺陷1处的散射信号

(d) 到达缺陷2处的散射信号

(e) 到达非缺陷处的散射信号

(a) 缺陷间距1=48 mm

(b) 缺陷间距2=18 mm

图7 不同缺陷间距下的拓扑能量成像结果

Fig.7 Topological energy imaging results for different defect spacing

3.2 实验与结果

实验成像系统由M2M超声激励接收仪、探头、铝板和Multi2000软件构成。设置M2M超声激励接收仪的采样频率为100 MHz。探头由16个线性排列的阵元组成，单个阵元长度为0.1 mm，宽度为10 mm，阵元间距为0.9 mm，中心频率为500 kHz。待测铝板长为300 mm，宽为150mm，板厚为2 mm。成像区域的大小为70 mm*25 mm。两个圆形通孔缺陷的半径均为5 mm，缺陷之间的距离=30 mm。

实验采用一发多收的信号采集方式。图8为第1阵元处激励，第5阵元处接收到的时域信号波形。频厚积为1MHz·mm时，接收到的兰姆波信号存在多个模式。

图8 第5 个传感器接收到的信号

3.2.1 延迟叠加算法实验结果

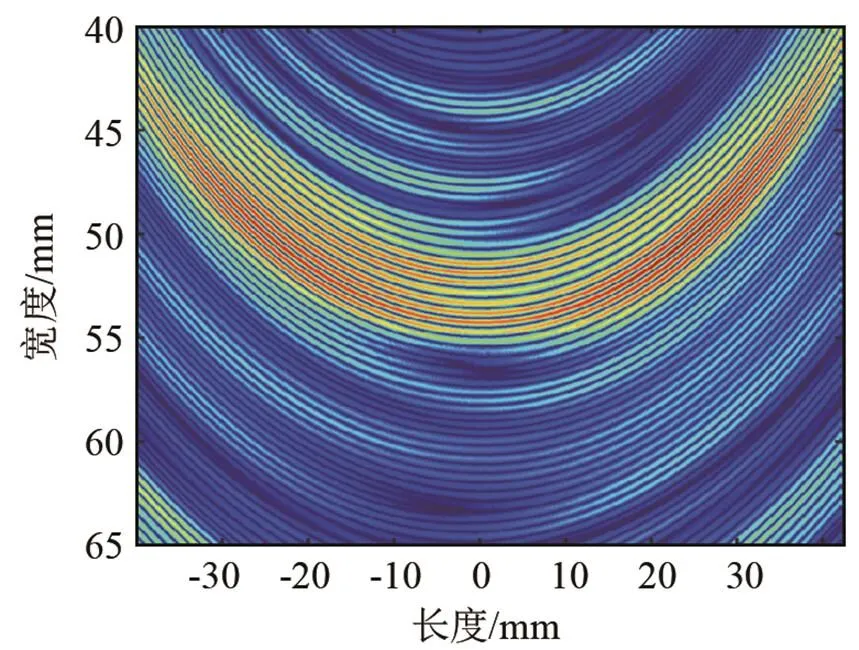
图9 缺陷间距ds=30 mm下的DAS成像结果

3.2.2 时域拓扑能量实验结果

现实生活中的兰姆波检测往往比仿真中的情况更为复杂。在多模式有噪声干扰的情况下，相应阵元重新激励后接收到的兰姆波信号在缺陷1和缺陷2处声束聚焦效果分别如图10(a)、10(b)所示。其中，最顶端的信号为直接声场中接收到的兰姆波信号，其他16组信号为伴随声场中接收到的兰姆波信号。非缺陷处的未聚焦的信号波形如图 10(c)所示。将时域拓扑能量法得到的图像进行融合，其结果如图11所示，显然，在多模式有噪声的环境下，时域拓扑能量法不仅可以确定两个缺陷的位置，还可以消除伪像。

(a) 到达缺陷1处的散射信号

(b) 到达缺陷2处的散射信号

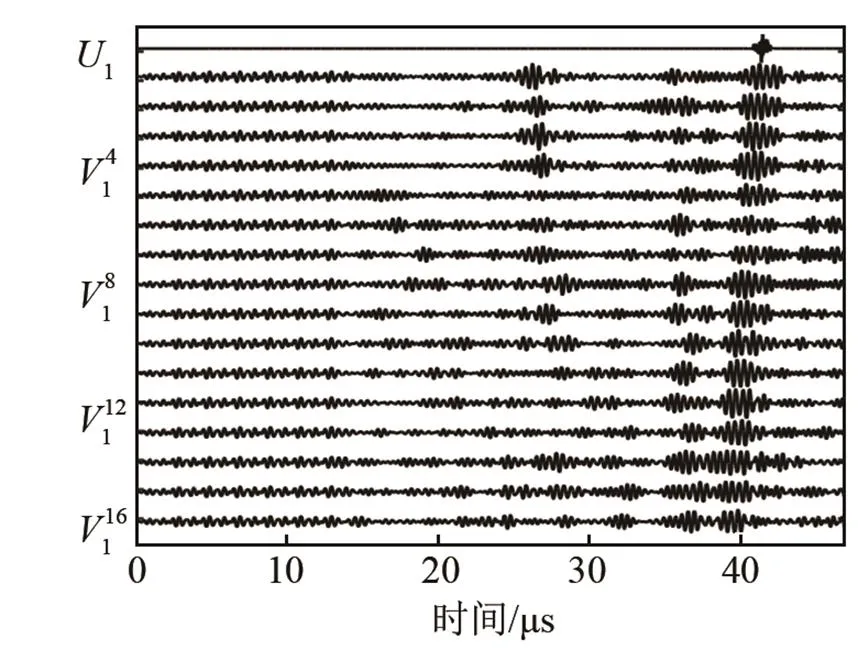
(c) 到达非缺陷处的散射信号

图11 缺陷间距d=30 mm下的时域拓扑能量成像结果

Fig.11 Time domain topological energy imaging results for thedefect spacingd=30 mm

4 结论

基于延迟叠加算法、时域拓扑能量法的检测原理，在多缺陷情形下，分别进行了有限元仿真和实际实验，并根据成像结果，重点从检测分辨率的角度对两种方法进行了相应的对比分析。

对于时域拓扑能量法而言：其仿真结果和实验结果均表明，由于该方法能够克服声波衍射的限制，因此可以实现两个缺陷的定位，另外图像融合还能够消除伪像的干扰，进而提高了检测分辨率。

综上所述，在进行多缺陷检测时，时域拓扑能量法明显优于延迟叠加算法。

[1] 张海燕, 于建波, 陈先华. 管道结构中的类兰姆波层析成像[J]. 声学学报, 2012, 37(1): 81-90.

ZHANG Haiyan, YU Jianbo, CHEN Xianhua. Lamb-like wave tomo-graphy of pipe structures[J]. Acta Acustica, 2012, 37(1): 81-90.

[2] 王卫威. 基于最优估计的SAR图像提高分辨率方法研究[D]. 长沙: 国防科学技术大学, 2008.

WANG Weiwei. Researeh on methods for resolution enhance- ment of SAR image based on optimal estimation [D]. Changsha: National University of Defense Technology, 2008.

[3] SYNNEVAG, J F, AUSTENG, A, HOLM S. Benefits of minimum-variance beamforming in medical ultrasound imaging[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2009, 56(9): 1868-1879.

[4] GUZINA B B, BONNET M. Topological derivative for the inverse scattering of elastic waves[J]. Quarterly Journal of Mechanics & Applied Mathematics, 2004, 57(5):161-179.

[5] DOMINGUEZ N, GIBIAT V. Non-destructive imaging using the time domain topological energy method[J]. Ultrasonics, 2010, 50(3): 367-372.

[6] 刘红飞. 基于自适应波束形成的超声成像算法研究[D].合肥: 中国科学技术大学, 2013.

LIU Hongfei. Study on ultrasound imaging algorithm based on adaptive beamforming[D]. Hefei: University of Science and Technology of China, 2013.

[7] 许琴. 超声成像中波束形成算法研究[D]. 重庆: 重庆大学, 2012.

XU Qin. Study on beamforming algorithm of ultrasound imaging[D]. Chongqing : Chongqing University, 2012.

[8] 李荣兴. 超声成像自适应波束形成方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.

LI Rongxing. Reserch on adaptive beamforming approaches in ultrasound imaging[D].Harbin: Harbin Institute of Technology, 2013.

[9] HAN C, CASSEREAU D, MINONZIO J G, et al. Numerical estimation of femoral neck cortical bone thickness based on time domain topological energy and sparse signal approximation[C]// European Symposium on Ultrasonic Characterization of Bone. IEEE, 2015: 1-4.

[10] GIBIAT V, SAHUGUET P. Wave guide imaging through time domain topological energy[J]. Ultrasonics, 2010, 50(2): 172-179.

[11] LUBEIGT E, MENSAH S, RAKOTONARIVO S, et al. Topological imaging in bounded elastic media[J]. Ultrasonics, 2017, 76: 145-153.

[12] SAHUGUET P, CHOUIPPE A, GIBIAT V. Biological tissues imaging with time domain topological energy[J]. Physics Procedia, 2010, 3(1): 677-683.

[13] RODRIGUEZ S, DESCHAMPS M, CASTAINGS M, et al. Guided wave topological imaging of isotropic plates[J]. Ultrasonics, 2014, 54(7): 1880-90.

[14] LEVINE R M, MICHAELS J E. Model-based imaging of damage with Lamb waves via sparse reconstruction[J]. J. Acoust. Soc. Am., 2013, 133(3): 1525-1534.

[15] 樊程广. 超声相控阵超分辨率成像方法研究[D]. 长沙: 国防科学技术大学, 2014.

FAN Chengguang. Research on approaches for super resolution imaging using ultrasonic phased array[D]. Changsha: National University of Defense Technology, 2008.

Multi-defect Lamb wave topological imaging

ZHANG Hai-yan, LI Jia-lin, XU Meng-yun

(Shanghai University, Shanghai 200444, China)

This paper combines time reversal theory with topology optimization ideas and introduces the concept of forward acoustic field and adjoint acoustic field. The time-inverted Lamb wave scattering signal is used as the secondary excitation source in the adjoint acoustic field, and the signal is focused at the defect. Then, the topological energy value of each point in the detection area is calculated according to the time domain topological energy formula. As a result, multiple defects in the sheet are characterized. Finite element simulations and experiments show that in the case of multiple defects, the delay-and-sum (DAS) method is unable to locate the defect when the defect spacing is smaller than the resolution threshold because of the constraints of the Rayleigh criterion; however, through Lamb wave time reversal focusing and image fusion, the time domain topological energy method can not only improve the defect detection resolution, but also eliminate the interference of artifacts in a multi-mode noisy environment. Lamb wave is effectively promoted in nondestructive testing of board structures.

time domain topologicalenergy; resolution; Lamb wave

TB559

A

1000-3630(2019)-05-0520-06

10.16300/j.cnki.1000-3630.2019.05.007

2018-07-23;

2018-09-13

国家自然科学基金资助项目(11674214, 11474195, 51478258)、上海市科委重点支撑项目(16030501400)

张海燕(1970－), 女, 山东曹县人, 博士生导师, 研究方向为超声无损检测。

张海燕,E-mail: hyzh@shu.edu.cn