时间分辨力约束下目标检测的波形优化设计

周飞

时间分辨力约束下目标检测的波形优化设计

周飞

(上海船舶电子设备研究所，上海 201108)

以最大化检测概率为优化准则，采用基于凸优化和随机化方法的具有相似性约束的相位编码算法(Phase Coding Algorithm with Similarity Constrain, PCA-SC)来设计发射波形，解决了主动声呐系统增大探测目标发射功率却不能提高检测概率的问题。同时，为有效降低PCA-SC算法所设计编码自相关函数的整体旁瓣级，提高其检测微弱目标的能力，在PCA-SC算法的基础上，结合新循环算法(Cyclic Algorithm-New, CAN)多相编码技术，提出了基于CAN的PCA-SC波形优化方法(Cyclic algorithm-new Phase Coding Algorithm with Similarity Constrain, CAN-PCA-SC)。仿真实验结果表明，PCA-SC和CAN-PCA-SC两种波形优化方法获得的发射信号均能够在满足系统所需时域分辨能力的要求下，实现检测概率的最大化，提高了目标检测性能，将时域分辨能力和检测性能有效地统一起来。相比PCA-SC波形设计方法，CAN-PCA-SC波形设计方法在保证获得的发射信号的检测概率优化效果一致的情况下，具有更低的积累旁瓣水平和更好的检测微弱目标的能力。

波形优化设计；自相关旁瓣级；旁瓣抑制；凸规划；检测概率

0 引言

主动声呐系统主要包含主动发射和主动接收两部分，在水下探测场景中，若已知重点关注区域，可通过主动发射部分发射携带一定参数信息的脉冲序列，对特定区域进行声波照射，通过回波分析来提取目标信息。因此，发射波形设计和回波数字信号处理在主动声呐系统中至关重要。对于发射波形的研究主要分为两方面，一是根据探测需求选择与之匹配的发射波形，二是通过信号处理实现探测和发射信号的最佳匹配，后者更具普适性，也是本文研究的重点。主动声呐系统波形设计是以系统对于目标信息的要求和干扰背景为依据的，信道不同，目标运动规律和主动声呐系统跟踪目标的阶段不同，对所设计波形的性能指标的要求是不同的，设计满足不同作战需求的最佳波形有很重要的现实意义。常用的声呐波形主要包括单频信号、调频信号和相位编码信号等，多相编码信号因具有较大的多普勒容限和较低的自相关旁瓣而备受关注[1]。常见的多相编码有P3码序列、P4码序列、Frank码序列、Golomb码序列、Chu码序列等，其中P3码的固有缺陷是通过匹配滤波的输出之后有较高旁瓣峰值。主动声呐系统探测静止目标时，多普勒频移为零，模糊度函数简化为自相关函数，旁瓣抑制问题就转化为最小化自相关函数的旁瓣级[2-3]。在多目标环境中,旁瓣峰值过高会造成检测目标的丢失，以及弱目标的检测性能差等问题，针对此类问题，STOICA等利用自相关函数的整体旁瓣级(IntegrateSidelobe Leve)作为代价函数来设计相位编码，有效提高了信号检测微弱目标的能力[4]。但基于ISL的最小化而设计的波形只考虑了在时域上分辨多个目标的问题，并没有考虑对目标的检测能力，尤其是对环境的适配能力。KAY考虑了杂波和混响都已知的条件下，设计出了有最佳检测效果的发射波形[5]，JACKSON根据功率谱的平方根误差组成的代价函数来进行发射波形优化设计[6]。前面学者讨论的多相位编码波形设计方法，仅仅只考虑了时间(距离)分辨力或者最佳检测中的一个，实际应用中，应根据作战需求，对时间分辨力和最佳检测性能综合考虑。PCA-SC算法设计出了一种综合时域分辨能力和检测概率的发射波形[7]。但PCA-SC算法所设计相位编码信号存在旁瓣峰值过高，会造成弱目标丢失的问题，本文提出了基于CAN方法的多相编码波形优化方法(CAN- PCA-SC)，对PCA-SC所设计的相位编码信号的旁瓣峰值与积累旁瓣水平进行了有效抑制，设计的发射波形有更高品质因数，更强的检测微弱目标能力。

1 时间分辨力约束下目标检测波形优化设计

1.1 PCA-SC波形优化设计原理

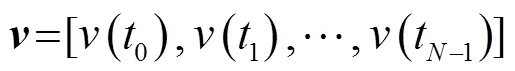
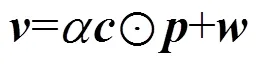
非波动目标(Non Fluctuate Target, NFT)检测概率可表示为

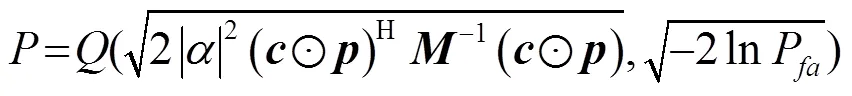
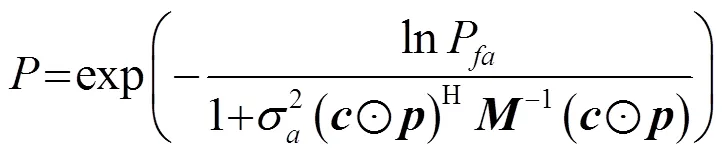
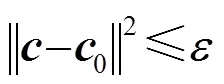
1.2 PCA-SC波形优化方法

通过以上分析，当噪声环境的协方差矩阵已知时，时间分辨力约束下目标检测最大化的相位编码设计的数学模型为[8]

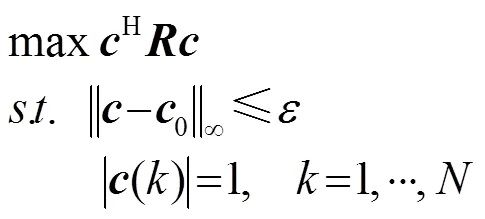
式(8)是一个具有有限约束的非凸约束二次规划问题(Quadratically Constrained Quadratic Programming, QCQP)，难以求解，它的半正定(Semidefinite program, SDP)松弛问题可能只有秩大于或等于1的最优解。文献[7]介绍了一种近似算法来求问题(8)的可行解，使用了SDP松弛、三角多项式的表示和秩为1的矩阵分解来求最优解。

2 基于新循环算法的多相编码波形优化

2.1 波形设计的代价函数与品质因数

离散信号的自相关函数可表示为

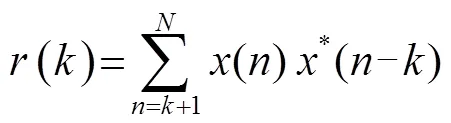
对于离散序列，定义一个代价函数：

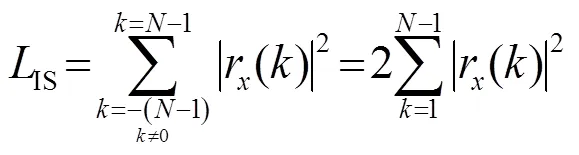
定义品质因数(Merit Factor, MF)：

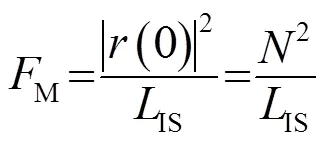
2.2 CAN优化算法

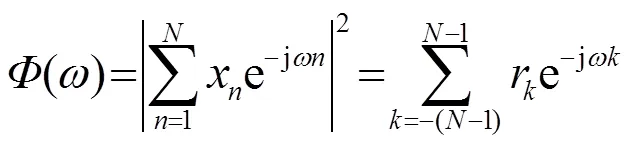
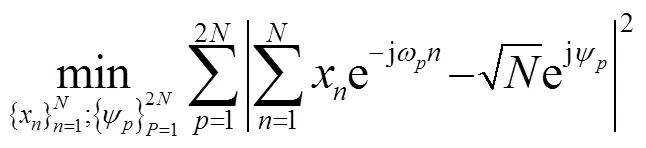
算法求解步骤：

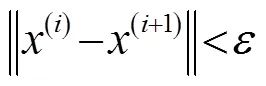
3 基于CAN的PCA-SC编码技术

为有效降低PCA-SC算法所设计编码信号自相关函数的整体旁瓣级，增强其微弱目标的检测能力。提出一种基于CAN的PCA-SC编码技术。具体设计思路如图1所示。

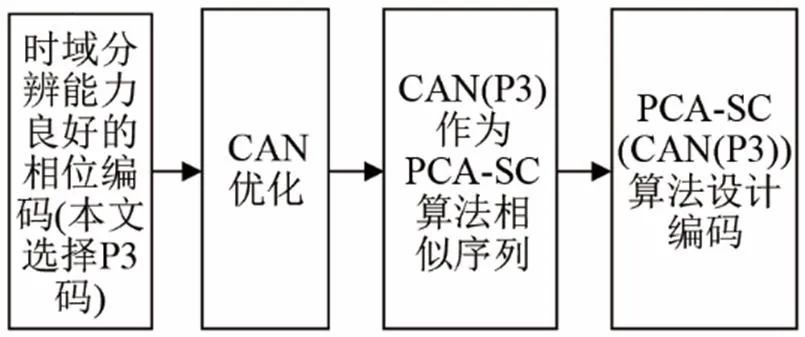
图1 CAN-PCA-SC编码设计原理框图

4 计算机仿真与分析

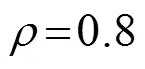
4.1 PCA-SC(P3)和PCA-SC(CAN(P3))算法设计编码检测概率曲线

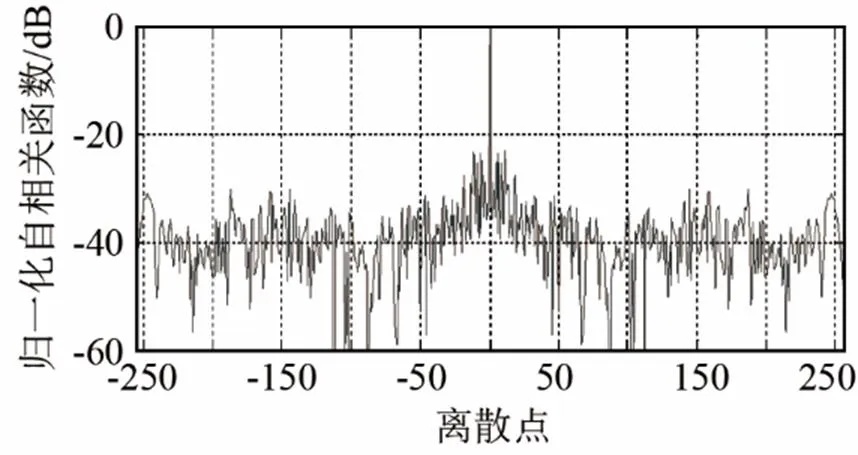
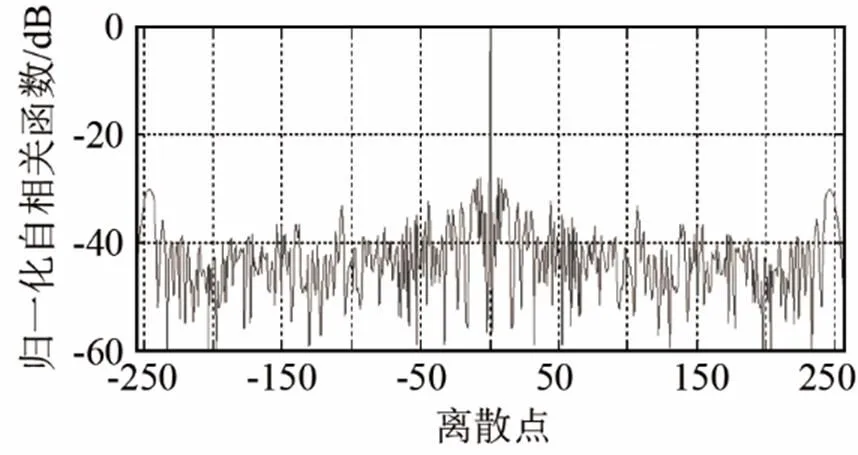
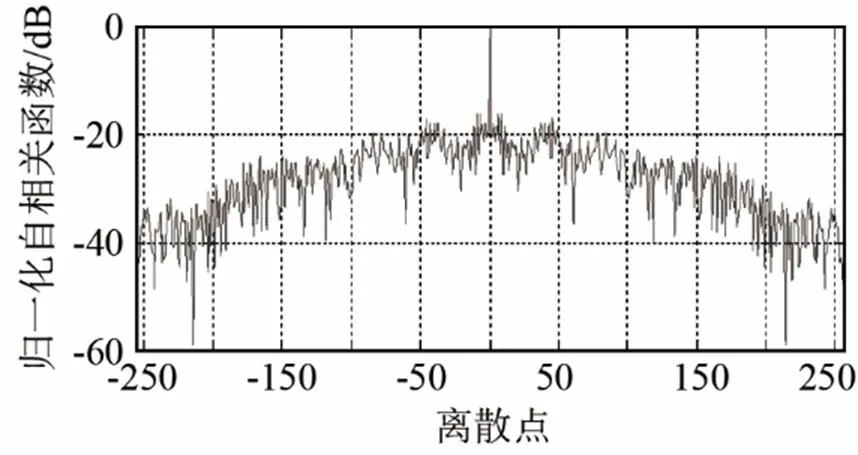
由图2可以看出，越大，PCA-SC算法设计编码检测概率越大。根据式(8)，相似性系数控制着设计编码和相似序列的相似程度，相似性系数越小，设计编码和相似编码越来越相似，这可以从图2检测概率曲线上得到体现，从归一化自相关函数图(图4～8中的(a)图部分)也得到了体现。

在图3中PCA-SC编码的相似序列为CAN(P3)码时，越大，设计编码检测概率越大，图4～8中的图(b)为其对应的归一化自相关函数图。对比图2、3可以发现，随着相似性系数减小，两种相似序列所设计的PCA-SC编码检测概率曲线和自相关函数图变化趋势一致，表1具体分析了相似序列分别为P3和CAN(P3)时所设计的PCA-SC编码，在不同相似性系数和信噪比下检测概率的具体值。

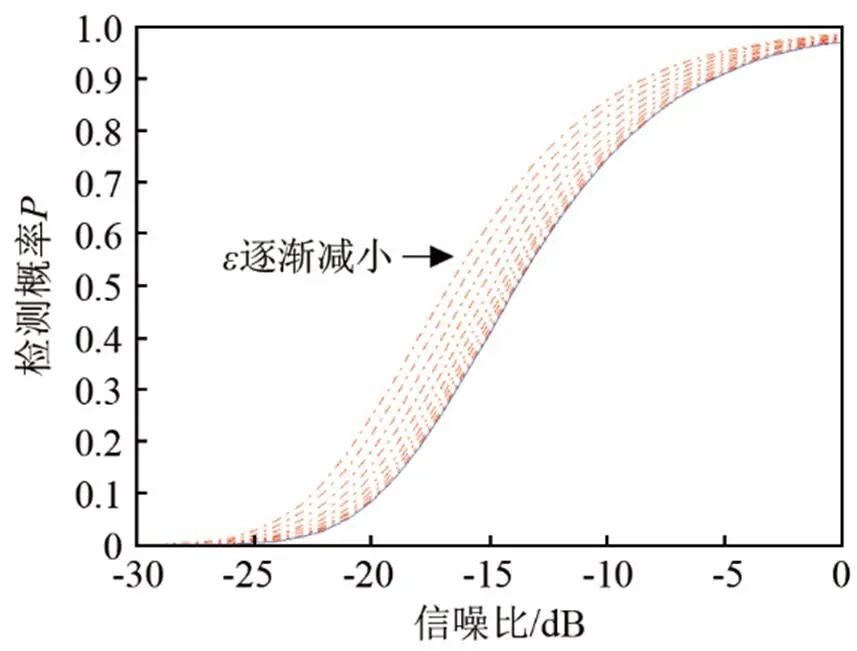
图2 P3码(蓝色实线)和 PCA-SC码(其相似序列为相同长度的P3 码)(红色虚线)的检测概率P随信噪比参数的变化曲线

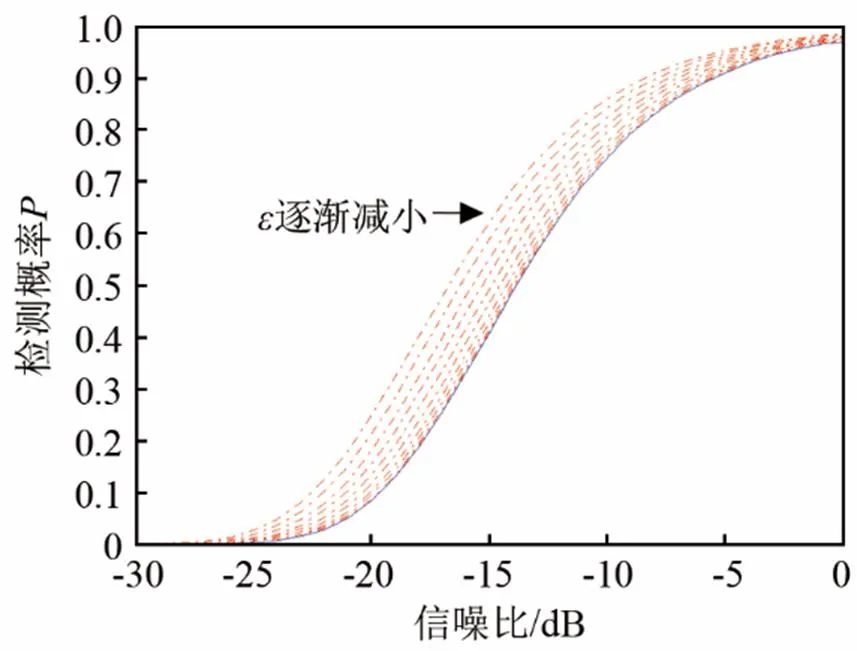
图3 CAN(P3)码(蓝色实线)和 PCA-SC码(其相似序列为相同长度的CAN(P3)码)(红色虚线)的检测概率P随信噪比参数的变化曲线

分析表1，可以发现，仅仅从检测概率方面分析，当相似性参数、信噪比相同时，PCA-SC(P3) (PCA-SC编码的相似序列为P3码)和PCA-SC (CAN(P3))(PCA-SC编码的相似序列为CAN(P3))编码的检测性能几乎一致。但从时域分辨力判断(对比仿真2图4～8可以发现)当相似性系数相同时，PCA-SC(CAN(P3))算法所设计的编码有更低的旁瓣峰值与积累旁瓣水平，更高的品质因数以及微弱目标检测能力。综合归一化自相关函数图(图4～8)和检测概率曲线(图2～3)，得出结论：CAN算法对P3码优化后，作为PCA-SC编码的相似序列，相比P3码直接作PCA-SC编码的相似序列时所设计编码检测概率几乎一致，但PCA-SC(CAN(P3))算法所设计编码有更低的旁瓣峰值与积累旁瓣水平，更高的品质因数以及微弱目标检测能力。

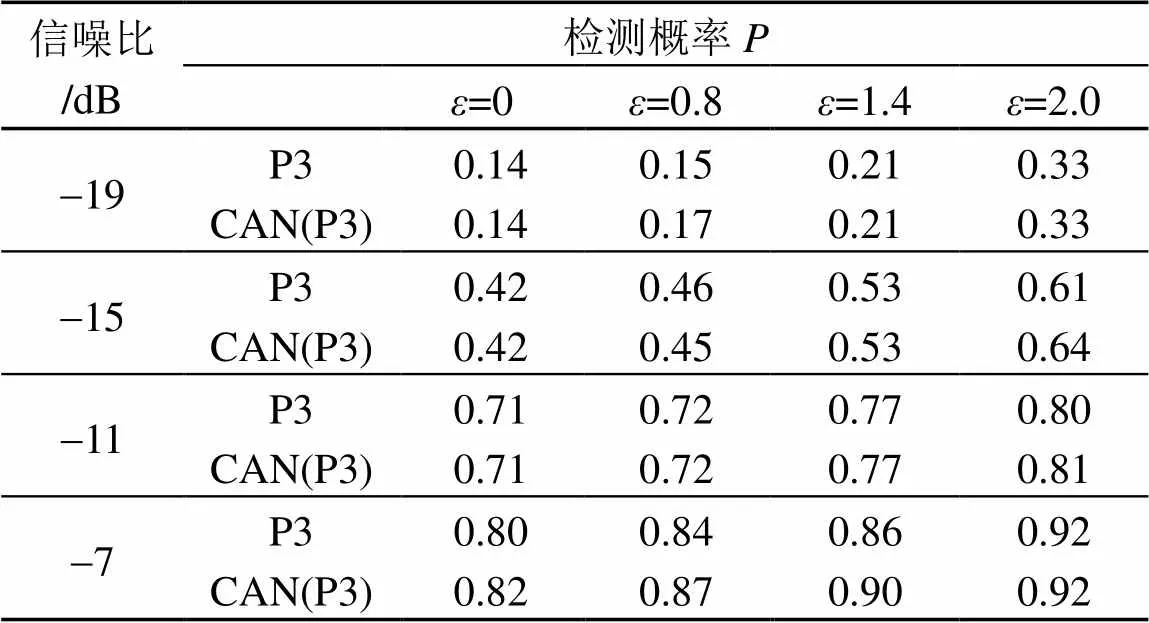
表1 不同相似系数ε条件下PCA-SC和CAN -PCA-SC算法所设计编码检测概率(P)随信噪比的变化情况

4.2 PCA-SC(P3)和PCA-SC(CAN(P3))算法设计编码归一化自相关函数图

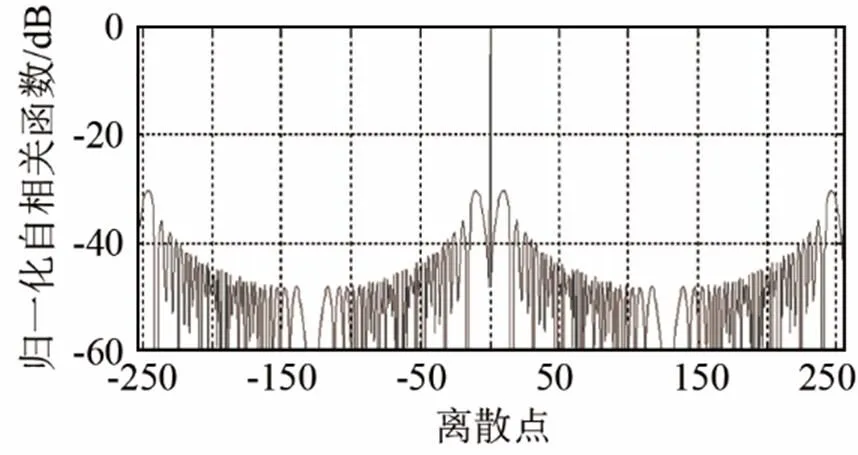
(a) PCA-SC(P3)

(b) PCA-SC(CAN(P3))

图4 相似系数=0时PCA-SC(P3)码和PCA-SC(CAN(P3))码的归一化自相关函数

Fig.4 Normalized auto-correlation functions of PCS-SC (P3) code and PCA-SC (CAN(P3)) code when=0

(a) PCA-SC(P3)

(b) PCA-SC(CAN(P3))

图5 相似系数=0.4时PCA-SC(P3)和PCA-SC(CAN(P3)) 的归一化自相关函数

Fig.5 Normalized auto-correlation functions of PCS-SC (P3) code and PCA-SC (CAN(P3)) code when=0.4

(a) PCA-SC(P3)

(b) PCA-SC(CAN(P3))

图6 相似系数=0.2时PCA-SC(P3)和PCA-SC(CAN(P3)) 的归一化自相关函数

Fig.6 Normalized auto-correlation functions ofPCS-SC (P3) code and PCA-SC (CAN(P3)) code when=0.2

(a) PCA-SC(P3)

(b) PCA-SC(CAN(P3))

图7 相似系数=0.8时PCA-SC(P3)和PCA-SC(CAN(P3)) 的归一化自相关函数

Fig.7 Normalized auto-correlation functions ofPCS-SC (P3)code and PCA-SC (CAN(P3)) code when=0.8

(a) PCA-SC(P3)

(b) PCA-SC(CAN(P3))

图8 相似系数=1.2时PCA-SC(P3)和PCA-SC(CAN(P3)) 的归一化自相关函数

Fig.8 Normalized auto-correlation functions ofPCS-SC (P3)code and PCA-SC (CAN(P3)) code when=1.2

表2 不同相似系数ε所设计的PCS-SC编码的品质因子FM

4.3 随机化次数对于检测性能的影响

图9展示了随机化次数对检测性能的影响。从图9中可以看出，10次随机化的曲线和100次随机化曲线非常接近，也就是说，这个算法具有收敛迅速的特性。

图9 随机化次数对检测性能的影响(L=[1,10,100,1000], ε=0.8)

5 结论

本文研究了主动系统探测静止目标的波形优化设计方法，首先介绍了PCA-SC算法来进行发射波形设计，以最大化检测概率为目标函数，并把时域分辨力作为约束条件，设计出一种综合时域分辨能力和检测性能的相位编码信号。在此基础上，提出了基于CAN的PCA-SC波形优化方法，相比PCA-SC波形设计方法，CAN-PCA-SC波形设计方法在保证获得的发射信号的检测概率优化效果一致的情况下，有更低的积累旁瓣水平和更好的检测微弱目标的能力。

[1] GINI F, De MAIO A, PATTON L. Waveform design and diversity for advanced radar systems[M]. London: The Institution of Engineering and Technology, 2012.

[2] 冯日博, 冯西安, 谭伟杰, 等. 基于新循环算法的多相编码波形优化[J]. 探测与控制学报, 2015, 31(1): 11-15.

FENG Ribo, FENG Xi’an, TAN Weijie, et al. Polyphase coded waveform optimization based on cyclic algorithm-new method[J]. Journal of Detection & Control, 2015, 31(1): 11-15.

[3] 张瑶, 梁国龙. 浅海条件下主动声呐目标探测若干方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013:1-10.

ZHANG Yao, LIANG Guolong. Research on methods of active sonar target detection in shallow water condition[D]. Harbin: Harbin Engineering University, 2013: 1-10

[4] STOICA P, HE H, LI J. New algorithms for designing unimodular sequences with good correlation properties[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1415-1425.

[5] STEVEN K. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter/reverberation[J]. IEEE Selected Topics in Signal Processing, 2007, 1(2): 31-34.

[6] JACKSON L, KAY S. Iterative method for nonlinear FM synthesis of radar signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 910-917.

[7] 周飞. 基于凸优化的最佳检测性能波形设计[J]. 声学与电子工程, 2018(4): 1-4, 17.

ZHOU Fei. Polyphase coded waveform optimization based on convex optimization method[J]. Acoustics and Electronics Engineering, 2018(4): 1-4, 17.

[8] De MAIO A, De NICOLA S, HUANG Y W. Design of phase codes for radar performance optimization with a similarity constraint[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 610-620.

[9] LEVANON N, MOZESON E. Radar Signals[M]. New York: Wiley, 2004.

Waveform optimization design of target detection under the constraint of time resolution

ZHOU Fei

(Shanghai Marine Electronic Equipment Research Institute, Shanghai 201108, China)

The PCA-SC (Phase Coding Algorithm with Similarity Constrain) algorithm based on convex optimization and randomization is proposed for transmitting signal design, which can improve the detection performance of active sonar for target parameter estimation in the presence of clutter. Furthermore, in order to detect weak targets, a new Cyclic Algorithm-New (CAN) based PCA-SC algorithm (termed as CAN-PCA-SC algorithm) is proposed. Through theoretical analyses and numerical simulations, it is shown that the signals designed by the two algorithms can maximize the detection probability while satisfying the requirement of time resolution, so that the performances of sonar detection and target parameter estimation are improved. Compared with PCA-SC algorithm, the CAN-PCA-SC algorithm has the capability of lower accumulated sidelobe level and better performance of detecting weak target under the condition that the detection probability optimization effect of the obtained transmitting signal is consistent.

waveform optimization design; sidelobe level of auto-correlation function; sidelobe suppression; convex optimization；detection probability

TN911.7

A

1000-3630(2019)-05-0594-06

10.16300/j.cnki.1000-3630.2019.05.019

2018-05-26;

2018-07-12

周飞(1988－), 男, 陕西渭南人, 硕士, 助理工程师, 研究方向为水声信号处理。

周飞, E-mail: 15601626468@163.com