应变控制方式下ZG270-500材料特性试验研究

张庆玲，张荣强，金 淼

(燕山大学 先进锻压成形技术与科学教育部重点实验室，河北 秦皇岛 066004)

0 引言

随着对材料性能研究的深入，在工程领域，人们不仅关心结构承载能力和使用安全等问题，而且对金属材料的本构研究也从原来的弹性范围和单调加载扩展到对循环载荷作用下弹塑性能的关注。但当前对循环载荷作用下的本构研究多集中于不锈钢、镁合金、铝合金、普通结构钢等金属材料，而对于工程领域广泛采用的铸钢的循环塑性本构研究却甚少。金属材料的应变循环特性是循环塑性变形的重要现象，同时也是循环塑性本构研究必须加以考虑的因素。

目前，国内外许多学者已经对循环载荷作用下材料的变形行为进行了大量的研究。万明珍和张再强等[1]对热循环作用下2A12铝合金进行了研究，得到了材料的变形行为与循环周次有关的结论。LAKHDAR T ，ZHOU Feng和MASAYUKI K等[2-4]研究了不同加载方式下304L和316L不锈钢的循环加载曲线，发现304L和316L不锈钢存在循环硬化现象。郑松林和程悦荪等[5]对中碳调质钢在低幅交变载荷作用下屈服强度增长规律进行了分析，得到了屈服强度与交变载荷大小和循环周次之间的关系。钱立和和刘帅等[6]研究了辙叉用高锰钢的循环变形与硬化现象，得到随着应变幅增大，辙叉钢循环硬化速率越快的结论。张庆玲和金淼等[7]研究了Q235材料的特性，得出了在小变形条件下Q235存在循环硬化现象和包申格效应的结论。石宝东和彭艳等[8]对AZ31镁合金各向异性力学性能进行了研究，得到轧制镁合金板材具有明显的各向异性力学性能和拉压不对称性的结论。施刚和王飞等[9]对Q460D进行了循环加载试验，得到了不同加载条件下Q460D的应力应变关系。吴旗和陈以一等[10]研究了Q460C在大应变条件下的循环加载试验，得到了钢材在大应变情况下的应力应变关系和滞回环特征。罗云蓉和王清远等[11]采用横向应变控制方法，得到了循环应力响应特征曲线。王建青和张兵等[12]对富锆锆钛二元合金力学性能进行研究，得到锆含量在70%～80%的合金表现出良好力学性能的结论。刘迪辉和庄京彪等[13]研究了金属薄板包申格效应，解释了试验中出现反向屈服应力减小和永久软化现象的原因。刘大海和孟维金等[14]对DP780高强钢板材进行了研究，得到了不同应变速率下的应力应变曲线。祝世强和杨微等[15]对TA15进行了研究，获得了在不同温度和应变速率下的应力应变曲线。虽然上述诸多学者已经对多种材料在不同循环加载条件下的力学性能进行了大量研究，但是鲜有学者对铸钢材料进行相关研究。

ZG270-500材料是许多大型设备机架的常用材料，如液压机的横梁等。本文通过不同应变控制下的循环加载试验，对应变控制下ZG270-500材料的循环变形特征进行了系统研究，深入了解此材料的循环特性，从而为研究其本构描述提供基础数据。

1 试样制取与试验设备

本次试验的材料为ZG270-500，主要化学成分如表1所示，铸坯尺寸400 mm×400 mm×180 mm，热加工工艺曲线如图1所示。

表1 ZG270-500钢材化学成分

Tab.1 Chemical composition of ZG270-500 steel %

图1 热加工工艺曲线

Fig.1 Heat treatment process curve

依据相关国家标准设计并加工单向拉伸和循环加载试样，其形状与尺寸如图2所示。

在室温下进行了应变控制条件下的单向拉伸和循环加载试验，试验均在最大载荷为100 kN，加载精度为200 N的电液伺服疲劳试验机(Instron8801)上进行。单向拉伸试验和循环加载试验均采用精度为0.1 μm，标距分别为25 mm 和12.5 mm的动态引伸计来测量轴向应变。

图2 试样尺寸图

Fig.2 Drawing of specimen size

2 单向拉伸材料性能研究

通过单向拉伸试验，获得了ZG270-500单向拉伸时的应力应变曲线，应力应变曲线如图3所示，同时也得到材料的弹性模量、屈服应力和抗拉强度等基本力学性能参数，参数见表2。

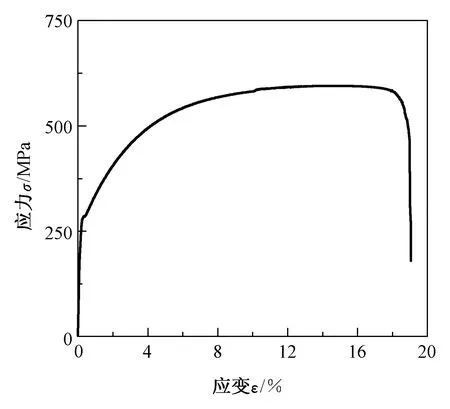
图3 单向拉伸应力应变曲线

Fig.3 Uniaxial tensile stress-strain curve

表2 单向拉伸试验结果

Tab.2 Results of uniaxial tensile test

应变速率/s-1弹性模量/GPa屈服应力/MPa抗拉强度/MPa断后伸长率/%断面收缩率/%0.2%180.13270.65608.7521.7424.82

由图3可知，ZG270-500在单向拉伸过程中虽然没有明显的屈服平台，但在屈服点之后出现了一段塑性模量较小，相对平缓的类平台区，类平台区的应变区间为0.27%～0.61%。试验测得，ZG270-500的屈服极限约为270.65 MPa，对应的应变为0.27%；强度极限约为608.75 MPa，对应的应变为15.5%。材料具有较高的伸长率和断面收缩率，表明其具有良好的塑性。

根据试验所得的数据，可以得到ZG270-500在单向拉伸塑性段(类平台区之后)力学模型表达式为

σ=900ε0.2，

(1)

其中，ε为总应变，总应变范围为0.61%～15.5%。

3 循环加载材料性能研究

依据单向拉伸试验获得的材料性能参数，设计对称应变控制的循环加载试验。设定应变载荷值大于材料屈服时对应的应变，共进行了6组加载试验，每组试验均测试3次，取平均值作为测试结果，试验方案中YB-01～YB-04为单级对称应变循环加载试验，YB-05和YB-06分别为应变幅值递减和应变幅值递增的多级对称应变循环加载试验，加载波形采用三角波，试验方案如表3所示。

表3 试验方案

Tab.3 Testing program

试验名称应变加载制度加载速率/s-1循环周次N/CYB-010.3%0.2%200YB-020.4%0.2%200YB-030.6%0.2%200YB-040.8%0.2%200YB-050.6%→0.4%→0.3%0.2%200/100/100YB-060.3%→0.4%→0.6%0.2%200/100/100

3.1 单级对称应变循环加载条件下材料性能研究

试验方案中YB-01～YB-03所施加的应变载荷均在类平台区，YB-04所施加载荷大于类平台区结束时的应变值，其对应的应力应变滞回曲线如图4所示。由图4可知，材料在循环第一周加载段与单向拉伸曲线形态基本一致，类平台区只出现在第一个循环周次的正向拉伸段，且第一周的应力值明显低于其他循环周次，即表示材料发生了循环硬化行为，并且循环硬化行为较明显。

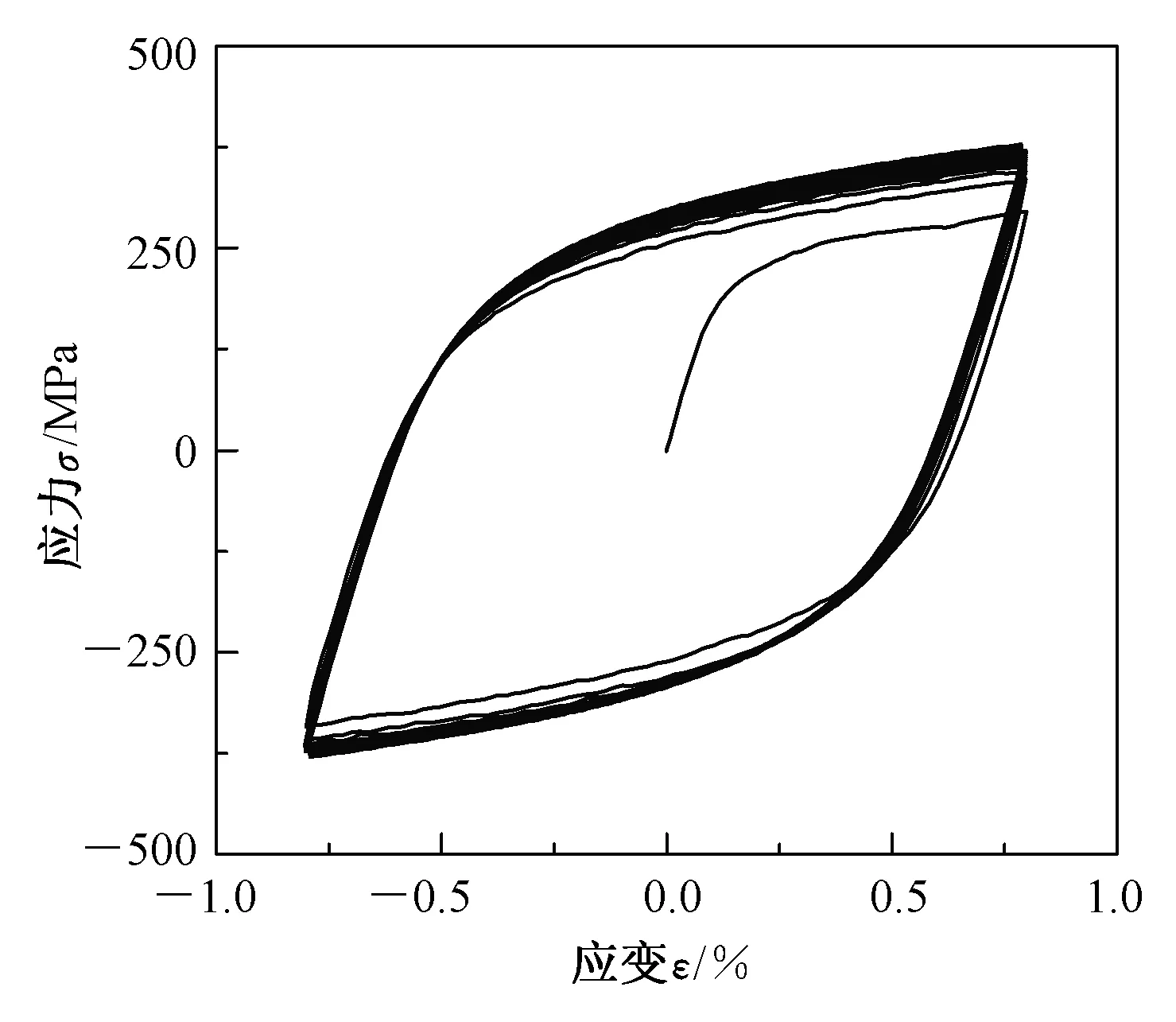
图4 对称应变幅值0.8%作用下应力应变曲线

Fig.4 Stress strain curve under the action of symmetrical strain amplitude 0.8%

图5描述了响应应力幅值随循环周次的变化规律，可以看出，四组试验均发生了循环硬化现象。将每个循环周次下的应力增长量称为材料的循环硬化速率。在初始10周内循环硬化现象非常明显，但循环硬化速率在不断降低，大约在经历50个循环后，循环硬化速率逐渐稳定于一个常数值。循环硬化速率与加载应变幅值的关系曲线如图6所示，可以认为两者之间具有良好的线性度。

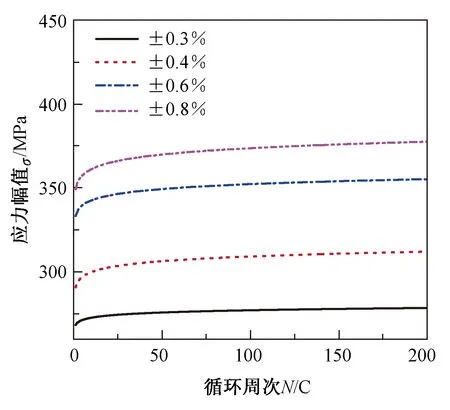
图5 响应应力幅值与循环周次曲线

Fig.5 Response stress amplitude and cycle curve

由以上分析可知，ZG270-500在小变形载荷作用下的循环硬化行为与外加应变载荷大小及循环周次有关，应变幅值越大，循环硬化行为越显著。循环硬化程度越高，意味着材料的动态承载能力越强。对于承受对称小应变量循环载荷的设备本体结构，这一特性可以一定程度上提高材料的许用强度极限。根据试验数据得到ZG270-500钢对称应变控制下响应应力幅值的表达式为

σ= [2 300εexp(N/14)+σNi]H(50-Ni)+

6(εN-σNi),

(2)

其中，ε为应变载荷值，N为循环周次，Ni为循环硬化速率稳定起始周次，这里取Ni=50；H(x)为Heaviside函数，当x≥0时，H(x)=1；当x<0时，H(x)=0。

图6 循环硬化速率与加载应变幅值的关系曲线

Fig.6 Relationship between cycle hardening rate and load strain amplitude

3.2 多级对称应变循环加载条件下材料性能研究

图7给出了两组试验中响应应力幅值随循环周次的变化曲线。从图中可以看出，未经历应变循环历史的响应应力幅值随循环周次的增加而增大，表现出循环硬化现象；经历先前较小的应变历史，后续加载应变逐级增加会使材料继续产生循环硬化，而经历先前较大应变历史，后续加载应变逐级减小会使其响应应力幅值减小材料呈现出软化现象。但比较经历了先前大应变历史以后，后续0.6%和0.4%循环时的响应应力幅值比未经历应变历史或经历较小应变历史条件下的相应的响应应力幅值有所增加。因此，对于受多级循环载荷作用的设备本体结构来说，在使用时可以通过先施加相对较大的载荷，然后再按要求施加工作载荷，人为提高其承载能力，以此来保护设备。

在应变载荷变化的初始50个循环周次内，ZG270-500的循环硬化和软化速率都较大，在50周以后逐渐稳定于非零的常值。循环硬化速率稳定值和循环软化速率稳定值如表4所示。

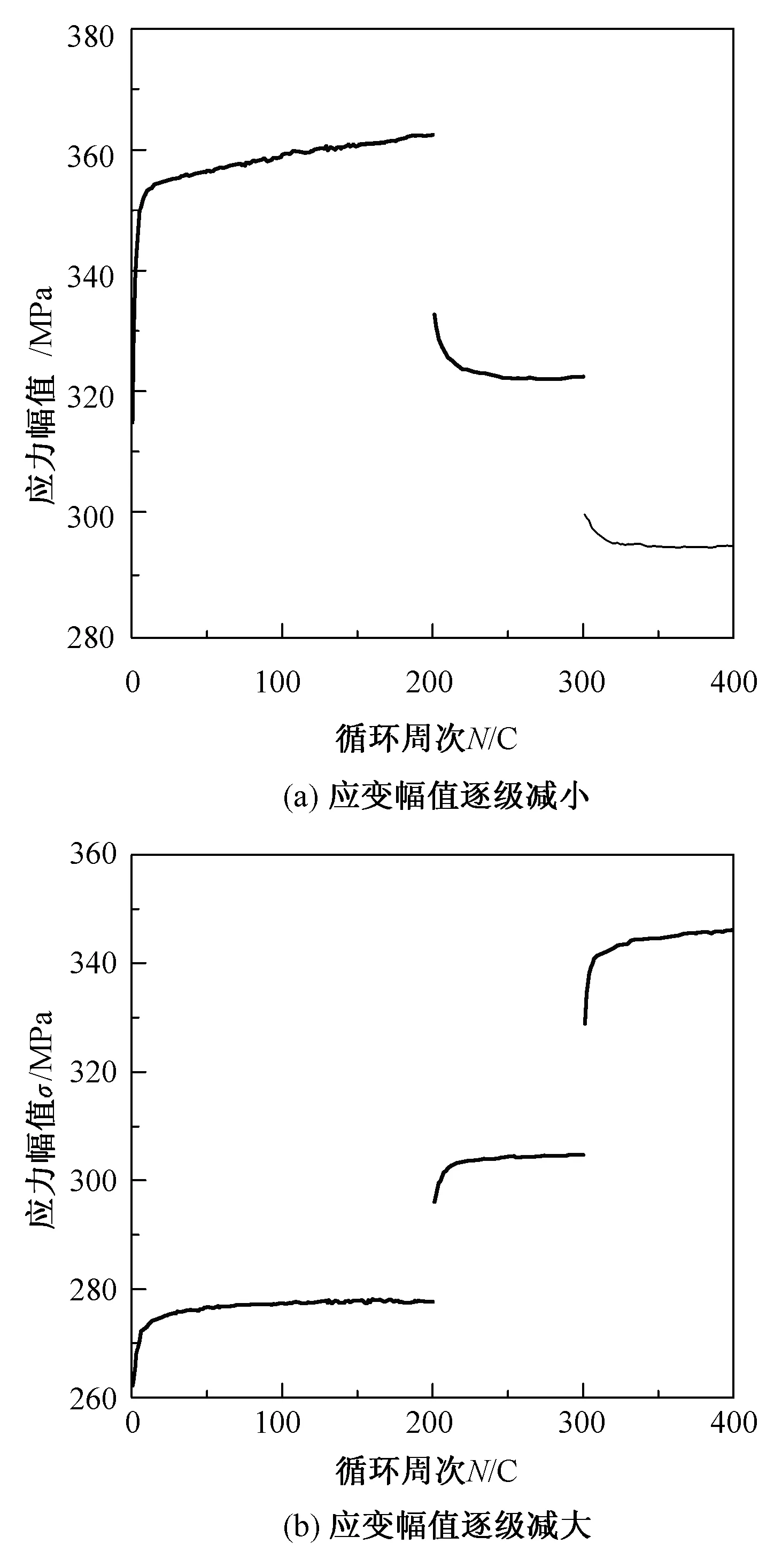
图7 响应应力幅值与循环周次曲线

Fig.7 Response stress amplitude and cycle curve

表4 循环硬化速率和循环软化速率稳定值

Tab.4 Stable values of cyclic hardening rate and cyclic softening rateMPa/C

应变幅值/%无加载历史应变幅值逐级减小应变幅值逐级增大0.30.008 9-0.001 10.008 90.40.021-0.002 40.0310.60.0300.0300.042

分析表4中数据可以看出，在多级应变循环加载试验中，较大的应变幅值加载历史改变了后续较小应变幅值下材料的循环硬化行为；在应变幅值逐级增大的试验中，有加载历史的比相同应变幅无加载历史的循环硬化速率的稳定值有明显的增大，前期较小的应变幅值加载历史对后期较大应变幅值下的循环硬化速率稳定值具有提升作用。

3.3 对称应变下材料包申格效应研究

金属材料经过预先加载产生少量的塑性变形后，卸载再同向加载，规定残余应力增加；反向加载，规定残余应力降低的现象，称为材料的包申格效应[16]。引入包申格应力参数对包申格效应的大小进行表征[17]，其表达式为

(3)

其中，σs,i是表示第i个加载分支时对应的屈服应力。当B>0时，材料表现出包申格效应；并且B越大，材料的包申格效应越明显。

各循环周次内的屈服应力均取σ0.2时对应的应力值，如图8所示。并依据式3计算出ZG270-500在不同拉压条件下的包申格系数。不同应变下ZG270-500钢材的包申格系数如表5所示。

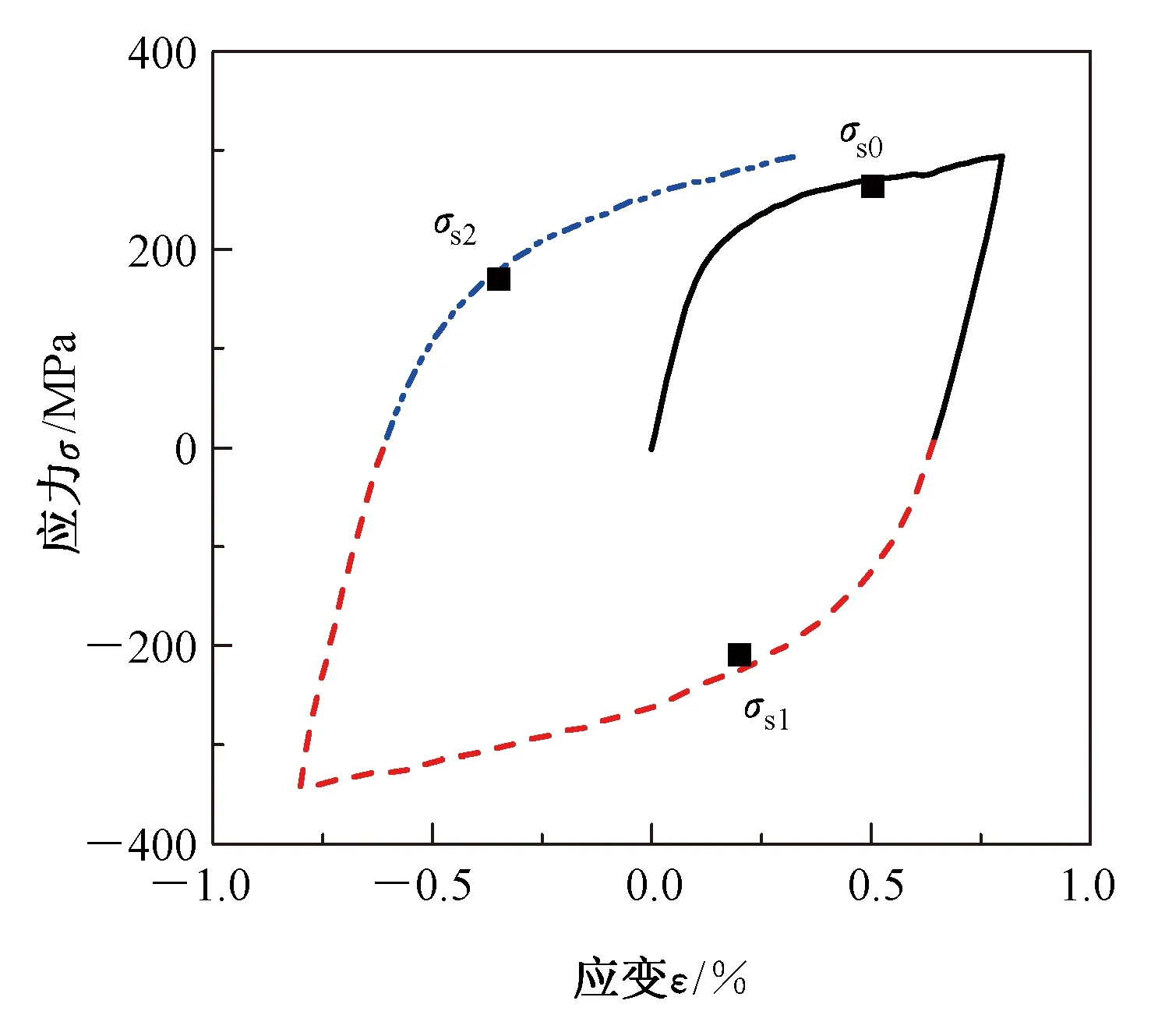
图8 循环应力应变曲线示意图

Fig.8 Schematic diagram of cyclic stress-strain curve

表5 ZG270-500钢棒材在不同应变幅值下的包申格系数

Tab.5 Bauschinger coefficient of ZG270-500 steel bar under different strain amplitude conditions

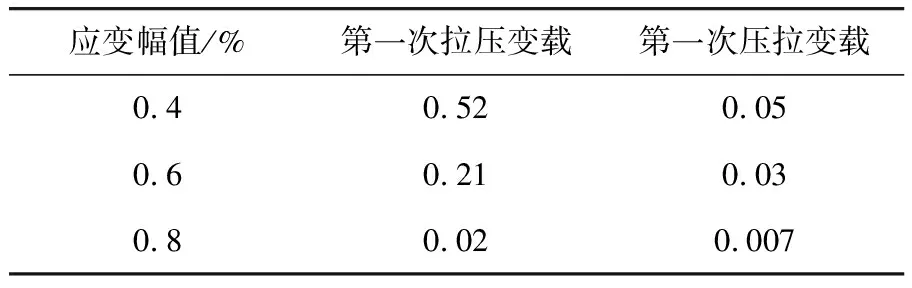
应变幅值/%第一次拉压变载第一次压拉变载0.40.520.050.60.210.030.80.020.007

由表5可以得出，ZG270-500钢在所有应变幅值情况下B>0，即材料表现出包申格效应。在同一应变幅值下加载时的包申格系数均大于反载时的包申格系数，即加载时的包申格效应大于反载时的包申格效应。应变幅值越大，加载和反载的过程中包申格系数逐渐减小即包申格效应越不明显。

4 结论

通过对ZG270-500进行小应变控制下的循环加载试验，在试验条件范围内，得出以下结论：

1)在室温下的单向拉伸试验中，ZG270-500钢出现类平台区，平台区应变范围0.27%～0.61%。

2)ZG270-500表现出较明显的循环硬化现象，循环硬化速率与加载应变幅值呈现良好的线性关系。

3)在多级应变循环加载时，前期较大的应变加载历史可以提高后期较小应变载荷下的响应应力幅值，即提高了后续的承载能力，对工作在此类条件下的设备使用具有指导意义。

4)在小变形量对称应变控制的循环加载情况下，ZG270-500表现出包申格效应，且随应变载荷的增加而减弱。