单项2 N 阶矩阵系数微分算子谱的离散性

钱志祥

(广东理工学院 基础教学部, 广东 肇庆 526100)

微分算子理论是当代量子力学的数学支柱，是解决数学物理方程以及大量科学技术应用问题的重要数学工具，参见文献[1-4].而微分算子谱理论是微分算子理论的中心内容，研究它有两方面的重要性：一方面，直接来自物理学与工程技术的需要；另一方面，微分算子谱理论是算子理论的一个分支.随着对Hamilton算子谱分布研究的深入，以及在逆谱问题迅速发展的同时，具有矩阵系数的微分算子的谱理论开始引起人们广泛的关注和兴趣[5-7].本文主要研究单项2 N 阶向量微分算式

τ(y)=(-1)n(P(x)y(n))( n),

x∈[0,).

(1)

当系数P(x)分别是实值矩阵函数和复值矩阵函数时，在其自伴和J-自伴定义域内(1)式所生成的微分算子的谱是离散的充分条件.

1 预备知识

引理 1.1[8]具有有限亏指数的对称算子T0的所有自伴扩张T具有相同的本质谱，而且等于对称算子的本质谱.

引理 1.2[9]若任何算子A是自伴算子A1、A2的直和，则A=A1⊕A2是Hilbert空间X上的一个自伴算子,而且

σ(A)=σ(A1)∪σ(A2)，

σp(A)=σp(A1)∪σp(A2)，

σc(A)=σc(A1)∪σc(A2)，

σd(A)=σd(A1)∪σd(A2)，

σe(A)=σe(A1)∪σe(A2).

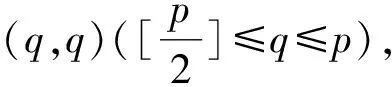
B=([φi,φj](b))1≤i,j≤2q-r，

则DM内线性流形D是τ(u(x))的自伴域的充要条件是存在q×p阶常数矩阵M和q×(2q-p)阶常数矩阵N满足下列条件：

(i) Rank(M⊕N)=q;

使得

D(T)={u(x)∈DM:MC(u)|a+

其中,Q(x)是Skew-Hemiltian矩阵，满足：

引理 1.4[12-13]设A是闭J-对称向量微分算子，def(A)=d<+，D(A)⊂D⊂D(JA*J)，D是A的J-自伴延拓的定义域的充分条件是存在{w1,w2,…,wd}⊂D(JA*J),使得：

1) {w1,w2,…,wd}模D(A)线性无关；

2) 〈wi,wj〉m=0,1≤i,j≤d；

3)D={u∈D(JA*J)|〈u,wj〉m=0,j=1,2,…,d}.

引理 1.5[14]设L1、L2是Hilbert空间 H 中的稠定闭线性算子，满足：

(a)L1和L2是对称的、半有界算子；

(b)D(L1)=D(L2)；

(c) 对某个复数λ0，集合R(L1+iL2-λ0I)(或者R(L1-iL2-λ0I))在Hilbert空间 H 内是稠定的；

(d) 对称算子L1+L2的Friedrich扩张算子的预解算子是全连续的;

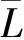
引理 1.6假设p(x)∈L1[0,)，p(x)>0，y(x)∈Cn0[0,)，则下列不等式恒成立:

(2)

证明先证当n=1时成立，由Cauchy-Bunyakovskii不等式得

(3)

又因为

(4)

由(3)和(4)式很容易得到不等式

(5)

由递推关系即得到不等式(2)成立.

引理 1.7对于任意的

(6)

证明先证

(7)

因为

(8)

由Cauchy-Bunyakovskii不等式得

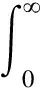
(9)

两端平方得

(10)

令α=2k-2,y=y(n-1)代入上式得

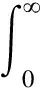
(11)

利用上式叠代得

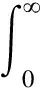
(12)

或者

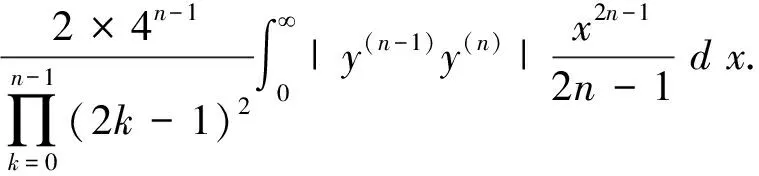
所以

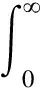
其中 C为常数.

引理 1.8设

u(x)=

其中ω=[x1,x2]为一有限区间.记

矩阵P(x)为定义在[0,)上的m×m阶实对称正定矩阵函数，pij(x)∈L1[0,),存在正交阵C(x)，使

C-1(x)P(x)C(x)=CT(x)P(x)C(x)=Λ，

其中Λ是以P(x)的m个特征值为对角元的对角阵.记λ1(x),λ2(x),…,λm(x)是实对称正定矩阵P(x)的m个连续的特征根函数，且

λ1(x)≥λ2(x)≥…≥λm(x),

则有下列不等式成立:

(14)

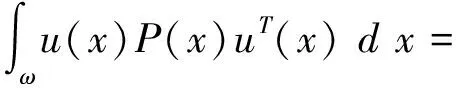
故

(15)

2 主要结论

定理 2.1设矩阵P(x)为定义在[0,)上的m×m阶实对角矩阵函数,

λi(x)∈L1[0,),i=1,2,…,m,且λi≥0 (i=1,2,…,m)，则由向量微分算式

τ(y(x))=(-1)n(P(x)y(n)(x))(n),

0≤x<+，

在其自伴域内生成的最小算子T0是自伴算子，T0的任何自伴扩张T的谱是离散的充分条件是

i=1,2,…,m.

(16)

证明由引理1.3知微分算式(1)在其自伴域内生成的最小算子T0是自伴向量微分算子，由引理1.1知其任何自伴扩张T具有相同的本质谱.假设条件(16)满足，即对∀ε>0,∃N,当x≥N时，有

再结合引理1.6和1.7得到

(17)

所以

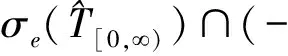
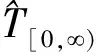
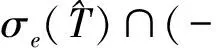
由ε的任意性，可以得到

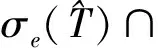
所以算子T的谱是离散的.

定理 2.2设矩阵P(x)为定义在[0,)上的m×m阶实对称矩阵函数，pij(x)∈L1[0,),i,j=1,2,…,m,且P(x)>0.记λ1(x),λ2(x),…,λm(x)是实对称矩阵P(x)的m个连续的特征根函数，且λ1(x)≥λ2(x)≥…≥λm(x),则由向量微分算式

τ(u(x))=(-1)n(P(x)u(n)(x))(n),

0≤x<+，

在其自伴域内生成的最小算子T0是自伴算子，T0的任何自伴扩张T的谱是离散的充分条件是

i=1,2,…,m.

(18)

证明由引理1.3知微分算式(1)在其自伴域内生成的最小算子T0是自伴向量微分算子.由引理1.1知其任何自伴扩张T具有相同的本质谱.因为P(x)为m×m阶实对称矩阵函数，故存在正交阵C(x)使得

C-1(x)P(x)C(x)=CT(x)P(x)C(x)=Λ，

其中Λ是以P(x)的m个特征值为对角元的对角阵.设

假设条件(18)满足，即对∀ε>0,∃N,当x≥N时，有下列不等式成立:

再结合引理1.6和1.7得到

(19)

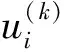
(20)

所以

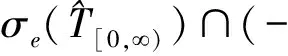
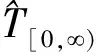
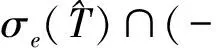
由ε的任意性，可以得到

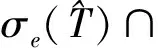
所以算子T的谱是离散的.

推论 2.3如果(1)式中系数p(x)是定义在[0,)上的纯量实值函数且p(x)>0,∀x≥0，则由微分算式(1)生成的算子T0的任何自伴扩张的谱是离散的充分条件是

i=1,2,…,m.

(21)

定理 2.4如果(1)式中的系数矩阵

P(x)=P1(x)+iP2(x),x∈[0,)，

其中P1(x)、P2(x)均为定义在[0,)上的m×m阶实对角矩阵函数，

设

λ1(x)≥λ2(x)≥…≥λm(x)≥0，

且

λi(x)∈L1[0,),

limx→+x2n-1∫x1λi(x)+λ′i(x)dx=0,

i=1,2,…,m.

(22)

证明由引理1.4知微分算式(1)在其J-自伴域内生成的最小算子T0是J-自伴向量微分算子.因为

τ(y)=(-1)n(P(x)y(n))(n)=

(-1)((P1(x)+iP2(x))y( n))(n),x∈[0,).

对上式进行分解得

τ1(y)=(-1)n(P1(x)y(n))(n),x∈[0,),

τ2(y)=(-1)n(P2(x)y(n))(n),x∈[0,).

设T10、T20、T0分别是由微分算式τ1、τ2、τ生成的最小算子，即

T10f=τ1(f),

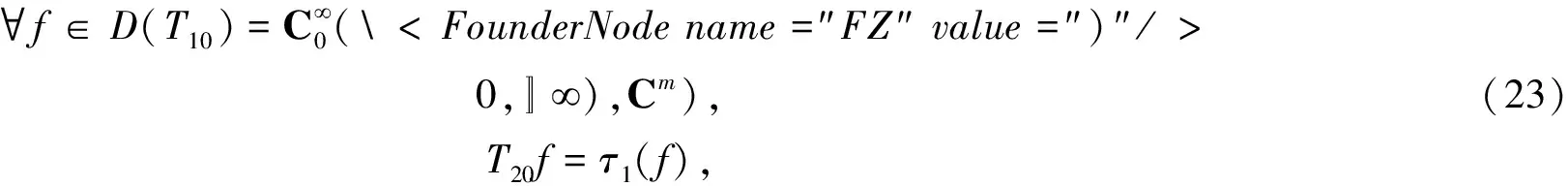
(24)

T0f=τ(f),

(26)

同理

Im(T0y,y)=(T20y,y)=

(27)

所以T10、T20也是下半有界的，说明了T10、T20满足引理1.5的条件(a)和(b).由(23)、(24)及(26)、(27)式可知

T0=T10+iT20，

T0的正则集非空，对于任何λ(Reλ<0,λ∈ρ(T0))，集合R(T10+iT20-λI)(或者R(T10-iT20-λI))在Hilbert空间 H 内是稠定的；说明了T10、T20满足引理1.5的条件(c).令

Ly=(T10+T20)y=(τ1+τ2)y=

(-1)n((P1(x)+P2(x))y(n))(n),

∀y∈D(T10)=D(T20),

(28)

则L=T10+T20是对称的,稠定下半有界的算子;利用条件(22),和定理2.1的证明方法一样可以证得:L=T10+T20的任何自共轭扩张的谱是离散的.从而根据引理1.5得:L=T10+T20的任何自共轭扩张的预解算子是全连续的，说明了T10、T20满足引理1.5的条件(d).

由上述讨论可知：T10、T20、T0满足引理1.5的条件(a)～(d),而且T0的正则集非空.利用引理1.5得：对于T0的任意J-自共轭扩张T，当λ∈ρ(T)时，(T-λI)-1是全连续算子，所以算子T0的任何J-自共轭扩张的谱是离散的.

定理 2.5如果(1)式中的系数矩阵

P(x)=P1(x)+iP2(x),x∈[0,)，

其中P1(x)、P2(x)均为定义在[0,)上的m×m阶实对称矩阵函数.记λ1(x),λ2(x),…,λm(x)是实对称正定矩阵P1(x)的m个连续的特征根函数，且

λ1(x)≥λ2(x)≥…≥λm(x)≥0，

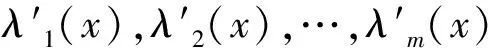
limx→+x2n-1∫x1λi(x)+λ′i(x)dx=0,

i=1,2,…,m.

(29)

证明由引理1.4知微分算式(1)在其J-自伴域内生成的最小算子T0是J-自伴向量微分算子.因为P1(x)、P2(x)为m×m阶实对称矩阵函数，故存在正交阵C1(x)、C2(x)，使

其中Λ1、Λ2分别是以P1(x)、P2(x)的m个特征值为对角元的对角阵.分别设为

因为证法和定理2.4相似,故这里只写出不同的地方.设T10、T20、T0分别是由微分算式τ1、τ2、τ生成的最小算子，下面只须证明T10、T20、T0满足引理1.5的条件(a)～(d)即可.

条件(b)和(c)的验证和定理2.4一样，这里省略不写，只验证条件(a)和(d).

对∀y∈D(T10)=D(T20)有

Re(T0y,y)=(T10y,y)=

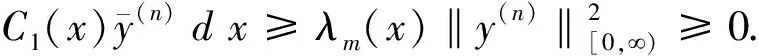
同理

Im(T0y,y)=(T20y,y)=

(31)

所以T10、T20也是下半有界的，说明了T10、T20满足引理1.5的条件(a).下面验证条件(d)，令

Ly=(T10+T20)y=(τ1+τ2)y=

(-1)n((P1(x)+P2(x))y(n))(n),

∀y∈D(T10)=D(T20),

(32)

则L=T10+T20是对称的、稠定下半有界的算子.利用条件(29),和定理2.2的证明方法一样可以证得:L=T10+T20的任何自共轭扩张的谱是离散的.从而根据引理1.5得:L=T10+T20的任何自共轭扩张的预解算子是全连续的,说明了T10、T20满足引理1.5的条件(d).所以T10、T20、T0满足引理1.5的条件(a)～(d)，所以算子T0的任何J-自共轭扩张的谱是离散的.

推论 2.6如果(1)式中的系数矩阵

P(x)=P1(x)+iP2(x),x∈[0,)，

其中P1(x)、P2(x)均为定义在[0,)上的m×m阶实对称矩阵函数.记λ1(x),λ2(x),…,λm(x)是实对称正定矩阵P1(x)的m个连续的特征根函数，且

λ1(x)≥λ2(x)≥…≥λm(x)≥0，

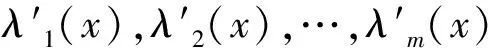
则由微分算式(1)生成的算子T0的任何J-自伴扩张的谱是离散的充分条件是：

i=1,2,…,m;

(33)

i=1,2,…,m.

(34)

定理 2.7如果(1)式中的系数矩阵

P(x)=P1(x)+iP2(x),x∈[0,)，

其中P1(x)、P2(x)均为定义在[0,)上的m×m阶实对称矩阵函数.记λ1(x),λ2(x),…,λm(x)是实对称正定矩阵P1(x)的m个连续的特征根函数，且是实对称正定矩阵P2(x)的m个连续的特征根函数，且

limx→λi(x)>0, limx→λ′i(x)>0,

i=1,2,…,m;

(35)

i=1,2,…,m.

(36)

证明对定理2.5的证明过程稍作修改即可证得.

推论 2.8[15]如果(1)式中系数

p(x)=p1(x)+ip2(x)

i=1,2,…,m.

(37)

推论 2.9[15]如果(1)式中系数

p(x)=p1(x)+ip2(x)

p1(x)>0,p2(x)>0, ∀x≥0，

则由微分算式(1)生成的算子T0的任何J-自伴扩张的谱是离散的充分条件是：

i=1,2,…,m;

(38)

i=1,2,…,m.

(39)

推论2.10[15]如果(1)式中系数

p(x)=p1(x)+ip2(x)

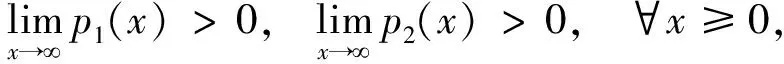
(40)

i=1,2,…,m.

(41)

例 1如果(1)式中的系数矩阵为

P(x)=

∀x≥0,

满足ai、bi(i=1,2,…,m)均是实数，并且

ai>0,bi>0,i=1,2,…,m，

max{αi,βi}>2n,i=1,2,…,m,

(42)

则算子T0的任何J-自伴扩张的谱是离散的.

例 2如果(1)式中的系数为

p(x)=axα+ibxβ, ∀x≥0，

满足a、b均是实数，并且

a>0,b>0， max{α,β}>2n,

(43)

则算子T0的任何J-自伴扩张的谱是离散的.

最后需要说明的是，定理2.1和定理2.2还可以研究必要条件，但是定理2.4、定理2.5、推论2.6和定理2.7的必要条件至今仍是个公开问题.

致谢广东理工学院科技项目(GKJ2016004)对本文给予了资助，谨致谢意.