返璞归真——让深度学习在课堂中生根发芽

蒋文

【摘要】新课改强调：培养学生的数学关键能力比教会学生某个知识点重要得多。其中有一个关键能力就是思考——深度学习。如何让深度学习在数学课堂中生根发芽？我们可以从以下四个方面展开：渗透方法，习惯的养成为深度学习保驾护航;问题引领，提问中激活深度学习的内在需求;经历过程，活动中促进数学思维的深度发生;杀个“回马枪”，对比中深度思考知识的本质属性。力求在平时的教学中，让深度学习在课堂中生根发芽。

【关键词】深度学习 渗透方法 问题引领

课堂中如何开展深度学习是新一轮课改的关键，作为数学教学如何开展深度学习更是迫在眉睫的事情。所谓深度学习，是指在理解学习的基础上，学习者能够批判地学习新的思想和事实，并把它们融入原有的认知结构中，能在众多思想中进行联系，并能将已有的知识迁移到新的情境中去，做出决策和解决问题的学习。结合一些资料及个人的思考，接下来从四个方面来谈谈如何让深度学习在课堂中生根发芽。

一、渗透方法，习惯的养成为深度学习保驾护航

让学生养成深度学习的习惯，还需要教师渗透学习方法，为深度学习奠定基础。笔者参考总结了以下学习方法：第一，学会主动预习。这是实施深度学习的基础性前提。让学生们课前学习，通过读书、圈画知识点，明确教材知识的基本内容，理解教材知识的基本精神，这是提高学生接受新知识、强化要点知识达成的基础。第二，掌握思考问题的方法。有些学生对各种公式、基本性质、概念、定义等背得挺熟，遇到上课刚讲的题目类型会套模式勉强完成，但只要题目稍微有点变化，就不知道从哪个方向思考，也不知道应用哪些知识来解答问题。所以，教师可以根据不同的类型讲解思考问题方法。第三，及时总结解题规律。引导学生做完题之后总结解题规律，并思考以下问题：（1）这道题有什么特点？（2）解决这道题需要用到哪些知识点？（3）用了什么数学方法？（4）这道题值得注意的地方是什么？（5）你能想到几种方法？这几种方法之间的联系和区别是什么？哪种方法最优？（6）有哪类题跟这题很类似？在解题中有什么相同与不同？把这些问题贯穿于解题的各个环节，边解题边思考，持之以恒，学生解题的心理稳定性和应变能力就可以不断提高，思维能力就会得到锻炼和发展。

掌握了这些学习的方法，学生遇到任何问题都能自我思考，由被动思考转化为主动思考，不仅提高了学生学习的积极性，更能加深学生思考的深度、厚度，为深度学习不断积累方式方法，也为深度学习提供了保障。

二、问题引领，提问中激活深度学习的内在需求

教学中应依据教学内容，巧妙地设计问题，提出有价值的数学问题，这就能把学生的数学思维引向深入，促使学生充分利用所掌握的知识、技能、经验以及数学思想方法。有效的设问既能促进学生思维的横向发展，又能促进学生思维的纵向延伸。

教师在教学中反复提出一些简单无效的问题：“明白了吗？”“你知道了吗？”……这些无效的问题只会让学生感觉幼稚无趣，作为数学教师我们要提有价值的、精练的问题。比如：“观察思考这类问题，你有哪些想法？”“是不是所有的题目都可以这样做？”这些问题会刺激学生深入地去探索、去发现。

例如：教学《平行四边形的面积计算》时，由于好奇，部分学生会主动自学这部分内容，所以他们会有一定的认识，按原来常规思路来教学已经不能满足部分学生的需求。所以，这节课可以利用三次自主探索，来探究平行四边形面积计算公式的推导。这三次自主探究都以问题驱动来展开。第一次问题引领：谁能利用已有的经验探索平行四边形面积计算公式的由来，再有层次地展示和交流作品呢？让学生初步感受面积计算公式的由来。当一切顺理成章，在学生以为明白了平行四边形的面积计算公式时，进行第二次问题引领：是不是所有的平行四边形都能用这个公式呢？引导学生再次深入思考。学生研究不同形状的平行四边形，体会面积计算公式的推导过程。接着教师插入视频，让学生从各个角度来观看平行四边形转化成长方形的割补演示过程，学生在比较中感知平行四边形面积计算公式的推导。第三次问题引领：请学生比较用木框做成的平行四边形转化成长方形，和上面用平行四边形转化成长方形有什么不同？长方形面积用邻边相乘，平行四边形面积能用邻边相乘吗？再次引导学生深入思考，从而对平行四边形面积有了更深、更全面的理解。

通过问题引领，让学生明确所要解决的问题，引导学生积极主动地进行思考，注意到事实背后的疑问，提出自己的困惑，再次引发学生深度思考，激起学习的内在需求。

三、经历过程，活动中促进数学思维的深度发生

数学课程标准指出：“有效的数学教学活动不能单纯地依赖模仿与记忆，动手实践、自主探究与合作交流是学生学习的重要方式。”因此在数学教学中，教师应根据教学内容的特点，提供相应的学具，精心设计有意义的教学活动，给学生提供探究的空间，激发学生探究的兴趣，给学生动手动脑的机会，让学生领略探究后的体验，理解知识的本质，在活动中促进数学思维的深度发生。

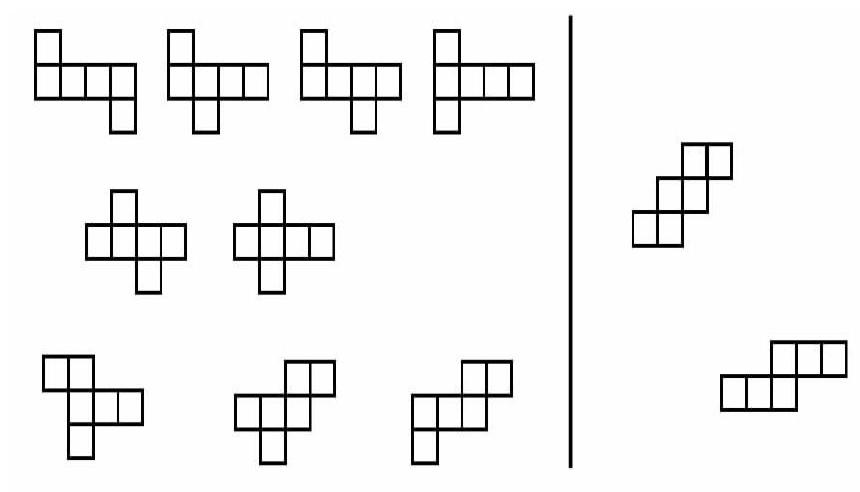
如教学苏教版六年级上册《正方体的展开图》时，在学生借助学具操作、观察思考等多种形式下建立正方体展开图的几种类型，这样设计：课前以小组为单位就座，每个小组准备好可以拼搭的同样大小的正方形磁力贴（可以贴在黑板上）。教师出示活动要求：（1）用磁力贴探索出正方体展开图有哪几种？（2）把这些展开图分分类。（3）说说你有什么发现？学生在小组内分工，2个人负责拼，2个人在方格纸条上画出拼搭成功的展开图，活动时派一小组的学生同时在黑板上拼搭。全班交流时，其他小组可以在黑板上已有的展开图中補充、删减，等到所有的展开图都展现后，再安排分类，总结出展开图的4种类型：一四一（6种）、二三一（3种）、二二二（1种）、三三（1种）。

教师适时提出问题：拼搭的展开图有什么规律？有没有什么值得注意的地方？学生经历了这个拼搭过程后，体会是比较真实的，会说到拼搭时不能出现田字格;中间四个面，上下各一面可以随意放;二二二像爬楼梯;三三由日相连。学生的回答是有感而发，也促进了学生数学思维的生长。在操作过程中，学生不仅得到了11种正方体展开图，而且在潜移默化中增加了找相对两个面的空间观念，为找相对的面奠定基础。在教学过程中，放手让学生参与到活动中来，经历知识的产生过程，这才是所谓的“既知其然，又知其所以然”。

四、杀个“回马枪”，对比中深度思考知识的本质属性

每天的内容教下来，一些学生会依葫芦画瓢，感觉已经会了，可只要稍微改变一下题型他们就会不知所措。为了突破学生的思维定式，我们在教学中当一切顺理成章、学生感觉学会时，适时杀个“回马枪”，指导学生运用比较的方法，通过比较分析、“找出”分析，找出异同、发现为难题，使学生对知识的可利用因素和混淆的因素进行辨析分化，让学生真正领会新授知识的精髓，自己重新建构知识体系。

如教学苏教版四年级上册《搭配规律》时，通过小组合作、亲自搭配，让学生经历从实物到图形、从具体到抽象的几个过程，引导学生有序地进行观察、发现、交流，使每个学生掌握搭配的规律，明白这个规律的本质：表示几个几用乘法来表示。但当所有的例题和练习都是同一种模式时，有的学生会依葫芦画瓢，不管是不是表示几个几，只要是今天这节课上的练习都可以套用。在学生认为一切都能熟练掌握时，教师时不时地安排一个“回马枪”。这节课中，教师设计了以下对比练习：

（1）常州到无锡，有2条铁路和3条公路，一共有多少种方法？

（2）学校到街心花园有2条路可走，街心花园到少年宫有3条路可走，从学校到少年宫一共有多少条路可走？

学生在解答时，两道题都列成2×3=6。这时，教师引导学生比较这两题有什么不同？明确第一题表示2种和3种，一共是5种;第二题表示的是2个3条或者3个2条，一共是6条，让学生在对比中进一步思考每一种搭配的本质，这里是几个几用乘法来表示，对搭配规律的认识提高到更高层次。

总之，教学生学习，不是灌输知识给他们，也不是打题海战，而是要激发学生学习的兴趣，渗透思考的方法，教师巧妙设计问题，让学生经历活动过程，启发学生主动去探索、思考知识的本质，引导他们深度思考，从求知过程中去组织属于他们自己的知识，从而促进思维的生长，让深度学习在课堂中生根发芽。