Cooperative Beamforming for Multi-Relay Networks with Limited Feedback

Jia Zhu,Ying Yao,Yulong Zou＊,Tong Wu

School of Telecommunications and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Abstract: In this paper,we consider a multi-relay cooperative communication network that consists of a source node transmitting to its destination with the help of multiple decode-and- forward (DF)relays.Specifically,the DF relays that succeed in decoding the source signal are allowed to re-transmit their decoded results simultaneously to the destination in a cooperative beamforming manner.In order to carry out the cooperative beamforming,the destination needs to send the quantized channel state information (CSI)to the relays through a limited feedback channel in the face of channel quantization errors (CQE).We propose a CQE oriented multi-relay beamforming (MRB)scheme,denoted CQE-MRB for short,for the sake of improving the throughput of relay-destination transmissions.An effective throughput defined as the difference between the transmission rate and the feedback rate is used to measure an outage probability of the source-destination transmission.Simulation results demonstrate that the outage performance of proposed CQEMRB scheme is improved substantially with an increasing number of relays.Moreover,it is shown that the number of channel quantization bits can be further optimized to minimize the outage probability of proposed CQE-MRB scheme.

Keywords: cooperative beamforming; relay selection; effective throughout; limited feedback; quantization error

I.INTRODUCTION

Recently,cooperative relaying technology has been recognized to improve the transmission reliability and coverage of wireless networks [1]-[5].There are two basic relaying protocols,namely the amplify-and-forward (AF)and decode-and-forward (DF)[6],[7].In general,the DF protocol has an advantage of achieving a better transmission reliability than the AF strategy,which comes at the cost of an extra decoding complexity and latency [8].In [9] and [10],the authors proposed a single “best” relay selection strategy for cooperative communications and showed that the diversity gain of single relay selection (SRS)is same as the number of total relay nodes.By contrast,the multi-relay selection (MRS)which allows multiple relay nodes to forward the source signal with the help of distributed beamforming can achieve a higher throughout than the SRS [11].The authors of [12] carried out the performance of a two-hop AF multi-input multi-output (MIMO)relay network with antenna correlation.In [13],a distributed transmit beamforming aided MRS scheme was proposed for cooperative DF relay networks along with its security-reliability tradeoff (SRT)analysis over Rayleigh fading channels.

Although the MRS scheme outperforms the SRS method in terms of transmission throughput,reliability and security [11]-[13],it relies on the distributed multi-relay beamforming which requires the full instantaneous channel state information (CSI)of transmission links spanning from the relays to destination.This results in additional channel estimation at the destination as well as the feedback overhead for sending the estimated CSI to the relays for distributed beamforming.In practical wireless systems,the feedback channel is very limited [14],which motivates the use of partial CSI knowledge [15],[16].In [17],the authors examined the optimization of training and feedback overhead for the sake of maximizing an effective sum-rate of MIMO Y channels.A CSI feedback overhead optimization problem was formulated in [18] to reduce the system resource consumption under the constraint of channel state reconstruction accuracy.Moreover,the authors of [19] investigated the distributed beamforming assisted relay subset selection with limited feedback.

In this paper,we consider a cooperative wireless system consisting of a source and a destination with the help of multiple relays with limited feedback in the presence of channel quantization error (CQE).We propose a CQE oriented multi-relay beamforming (MRB)scheme,referred to as the CQE-MRB.We define an effective throughput as the difference between the maximum data rate of relay-destination transmissions and feedback rate of sending the estimated CSIs,which is used to evaluate an outage probability of the CQE-MRB scheme.Simulation results demonstrate that the proposed CQE-MRB scheme significantly improves the outage performance of the source-destination transmission by increasing the number of relays.Moreover,it is also shown that the number of quantization bits per channel can be optimized to minimize the outage probability of our CQE-MRB scheme.

The remainder of this paper is organized as follows.In section II,the system model of a multi-relay cooperative network is briefly introduced.Section III proposes the CQE-MRT scheme for mitigating the adverse effect of CQE on system performance of the multi-relay cooperative network.Simulated outage probability results of the CQE-MRB are provided in Section IV.Finally,the conclusion is drawn in Section V.

II.SYSTEM MODEL

We consider a wireless relay network,which consists of one sourceS,one destinationDandMrelays,as shown in figure 1,whereRirepresents thei-th relay.There is no direct link betweenSandD,andStransmits its signals toDwith the help ofMrelays.Each node of figure 1 is considered to be equipped with a single antenna.It is of interest to consider an extension of our system model to heterogeneous wireless networks,which is left for future work.All wireless channels between any two network nodes are modeled as independent Rayleigh fading processes.Moreover,an additive white Gaussian noise (AWGN)with zero mean and a varianceN0is encountered at any receiver.

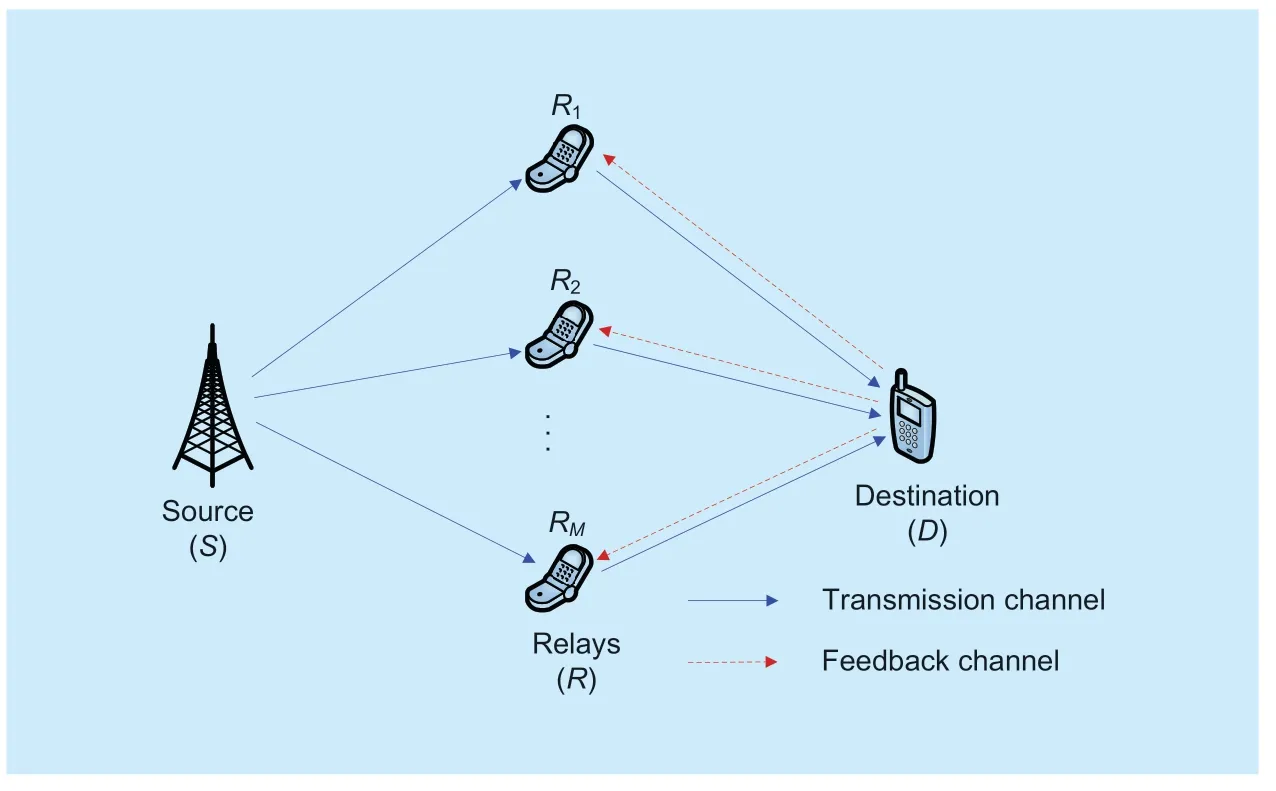
Fig.1.The system model of a cooperative relay network.

The procedure of an overall transmission from the source via relays to destination is divided into two phases.In the first phase,the source sends its signalxs(E(|xs|2)= 1)toMrelays with a power ofPsand data rate ofR,whereE(.)represents the expectation operator.Hence,the signal received at the relayRican be written as

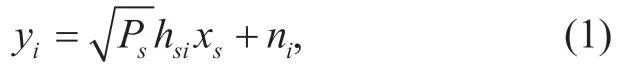
wherehsidenotes a fading coefficient of the channel fromStoRiandniis the AWGN received at the relayRi.From (1),we can obtain a receive signal-to-noise ratio (SNR)atRias

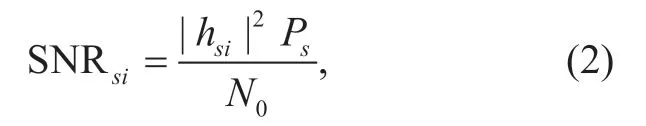
from which the channel capacity fromStoRican be given by

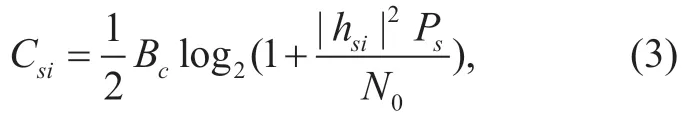
where the factor 1/2 arises from the fact that two orthogonal channels are needed for completing the signal transmission fromStoDviaRiandBcrepresents a channel bandwidth of the source transmission.From the Shannon's coding theorem,the relayRiis unable to decode the source signalxs,if the data rateRexceeds the channel capacity ofCsi.Otherwise,the relayRiis capable of successfully decoding the source signal and can forward its decoded result to the destinationD.Let us denoteDm(m∈ {1,2,… ,2M-1})as a nonempty set of relays succeeding in decoding the source signal,as described by

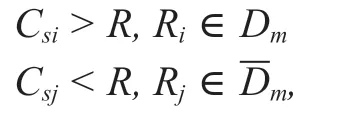
In the second phase,the relays which succeed in decoding are used to forward the source signalxsto the destinationD.If all relays fail to decodexs,the source signal would not be retransmitted from any relays toD,meaning that an outage event happens.Otherwise,all the relays withinDmare exploited to simultaneously transmitxsto the destinationD.To make an effective use of multiple relays,a beamforming vector of w=[w1,w2,…,wi,…,w|Dm|]Tis employed at the relays for transmittingxsand the vector of w should be normalized as ||w||=1,where|Dm|is the cardinality of the setDmandwirepresents the beamforming weight from thei-th relay toD.Moreover,channel coefficients from the multiple relays withinDmtoDare denoted by a channel vector of hd=[h1d,h2d,…,hid,…,h|Dm|d]T,wherehidrepresents a fading coefficient of the channel from thei-th relay toD.Throughout this paper,the channel coefficients ofhidfor different relays are assumed to be independent complex Gaussian random variables (RVs)with zero mean and a variance ofσi2d.Thus,the signal received atDcan be expressed as

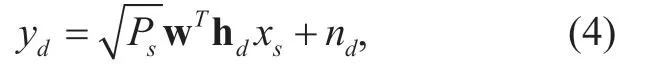
where wTrepresents the transpose of w andndis a zero-mean complex AWGN with a variance ofN0received at the destination.

In this paper,the CSI knowledge of hdis assumed to perfectly known at the destination through channel estimation [20],which needs to be fed back to the relays for the beamforming vector design.Since the feedback channel is bandwidth-limited,the continuous channel coefficients of hdknown atDhas to be quantized before feeding back to the relays.Thus,the channel coefficient received the relays can be represented aswheredenotes a quantized fading coefficient of the channel from thei-th relay toDandhiedenotes the corresponding channel quantization error.By denotingas a quantized channel vector andas a quantization error vector,the channel vector hdcan be written as

where the quantization errorshiefor different relay channels are modeled as independent zero-mean RVs with a variance ofσi2e,whereini∈{1,2,… ,|Dm|}.The distribution of the quantization errorhiedepends on our adopted quantization method,which will be discussed in following Section III-A.Substituting (5)into (4)yields

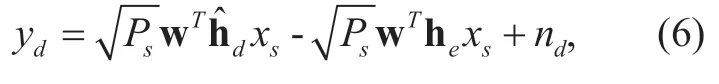
from which a receive signal-to-interference-and-noise ratio (SINR)atDis obtained as

where the expectation over an unknown quantization error vector heis given by

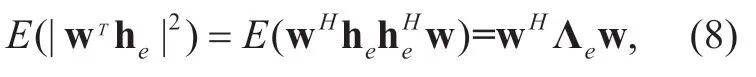
whereHdenotes the conjugate transpose operator,and I is a |Dm|×|Dm|identity matrix.Combining (7)and (8)yields

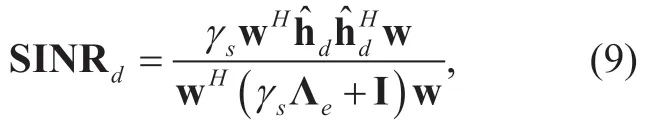
whereγss=P N/0.Based on the Shannon's capacity formula and using (9),we can obtain the channel capacity from the relays toDas

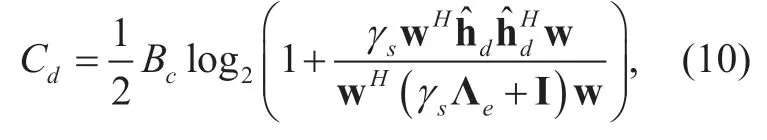
whereBcis a channel bandwidth of the source-destination transmission.

In our MRS scheme,all the intermediate relays inDmare selected to send the source signal toD.Assuming that all the relay channels are quantized using the same quantization method with the same number of quantization bitsNcper channel,we can obtain a feedback rate for sending the quantized CSIs fromDto relays as

where |Dm| is the number of relays which succeed in decoding,Ncis the number of quantization bits per channel,Tcis the coherence time of relay channels.

Using (10)and (11),an effective throughput of the relay-destination transmission is defined as the difference between the channel capacityCdand feedback rateRfas given by

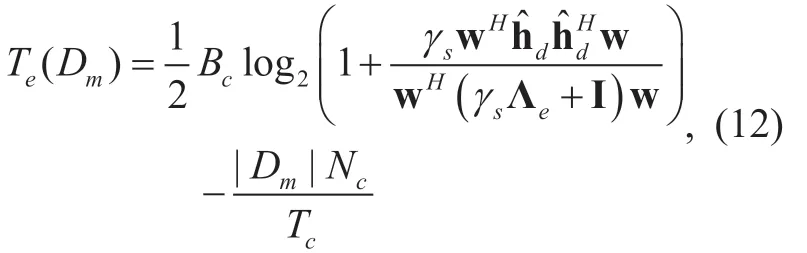
for the case ofDm,which is the effective throughput of the relay-destination transmission excluding the feedback overhead.

III.PROPOSED CQE-MRB SCHEME

In this section,we first introduce the channel quantization process.Next,a CQE-MRB scheme is proposed to mitigate the adverse effect of CQE on the throughout performance of relay-destination transmissions.

3.1 Channel quantization analysis

The quantization error ofhidrelates to the specific channel quantization method and the number of quantization bits per channelNc.Generally,different channel quantization methods have different quantization error distribution.Moreover,as the number of quantization bits increases,the quantization error decreases,and vice versa.Throughout this paper,the equal probability channel quantization is considered.It is of interest to examine the impact of different channel quantization methods on the system throughput,which is left for future work.Considering that the real and imaginary parts of a complex Gaussian channel fading both needed to be quantized withNcbits,we allocate one half of the total quantization bits for the real and imaginary parts,respectively,thus the number of quantization stepsNqis given byNq=2Nc/2.According to the principle of equal probability channel quantization,the total probability of either real or imaginary parts of a complex Gaussian fading is equally divided intoNqquantization steps.Denoting the real or imaginary parts of a complex Gaussian fadinghidbyx,we can express the thej-th quantization leveldjas given by

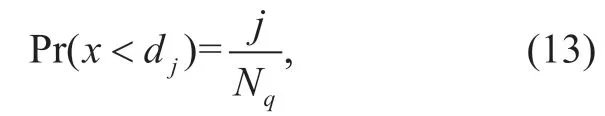
wherej∈{0,1， … ,Nq}.Since the random variablexis Gaussian distributed with zero mean and a variance of/2,thej-th quantization leveldjis obtained from (13)as

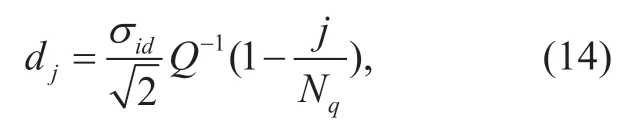
wherek∈{1,2,… ,Nq}.From (16),we obtain

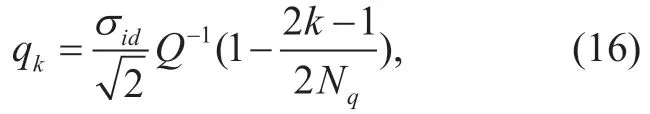
fork∈{1,… ,Nq}.As a consequence,we can obtain a variance of thefor the equal probability channel quantization method as

where Φjis given by

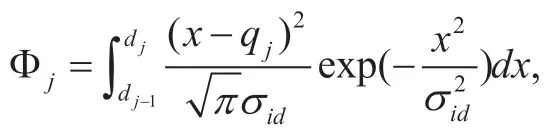
which leads to

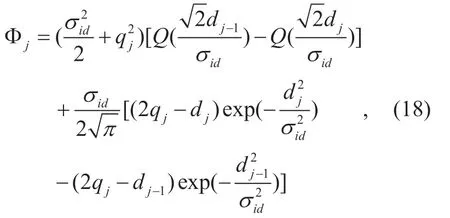
which completes the channel quantization analysis.

3.2 CQE-MRB design

In this section,we discuss the optimization of beamforming vector w for the sake of maximizing the receive SINR atDSINRd.According to (9),we can formulate an optimization problem of maximizing the receive SINRdatD,namely

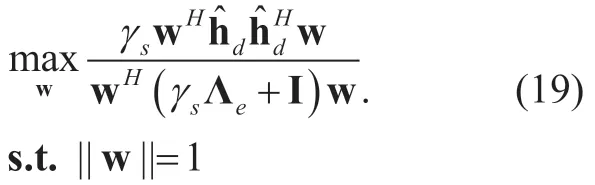
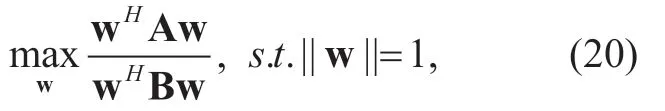
from which an optimal beamforming vector in the presence of CQE denoted by wCQEis obtained as

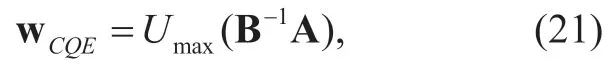
whereUmax(B-1A)represents the eigenvector associated with the largest eigenvalue of the matrix B-1A.Moreover,the maximal receive SINRdbecomes the largest eigenvalueλmax(B-1A)of the matrix B-1A.Therefore,we can obtain the channel capacity of relay-destination transmissions relying on our CQEMRB scheme as

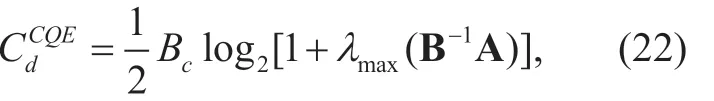
whereλmax(B-1A)represe nts the largest eigenvalue of the matrix B-1A.Substituting (22)into (12)yields an effective throughout of relay-destination transmissions for the proposed CQE-MRB scheme as

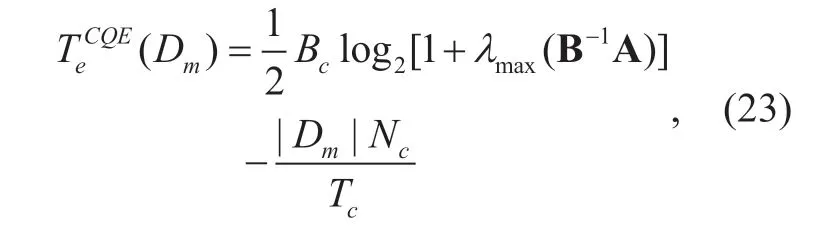
for the case ofDm.Moreover,if the relay-destination channels are independent identically distributed (i.i.d.)for different relays,the CQE variances ofbecome the same for different relaysi∈{1,2,… ,|Dm|},as denoted byIn this way,the optimization problem of (19)can be rewritten as

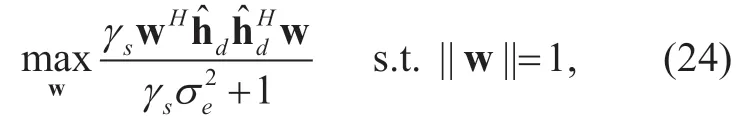
from which an optimal precoding vector is given by

which is the so-called maximal ratio transmission (MRT).It can be observed from (21)and (25)that the traditional MRT is a special case of our CQE-MRB scheme when the relay-destination channels are i.i.d.each with the same quantization method.

By using the law of total probability,an outage probability of the source-destination transmission relying on our CQE-MRB scheme is obtained as

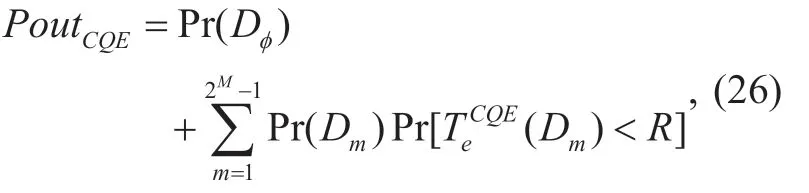
where Pr(Dφ)and Pr(Dm)are given by

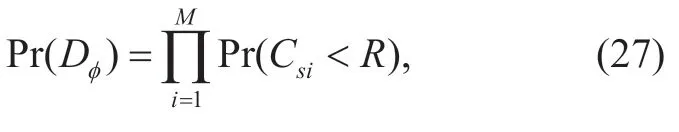
and

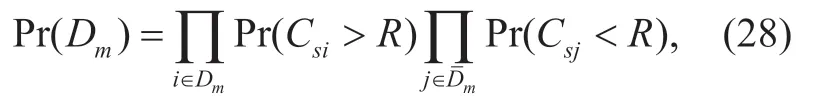
whereCsiis given by (3)andRrepresents a data rate of the source transmission.Using (3)and noting that the fading coefficients of|hsi|2for different relays are independent exponentially distributed RVs with a mean ofwe arrive at

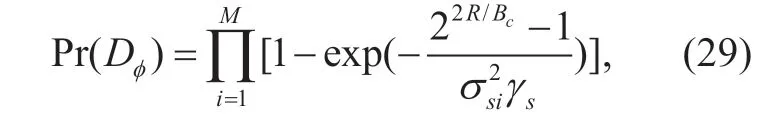
and

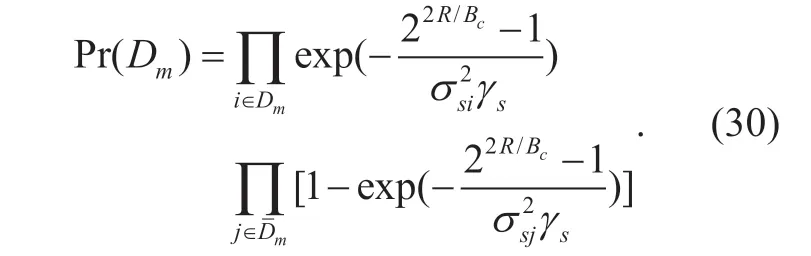
So far,we have presented the CQE-MRB scheme along with its outage probability analysis.

IV.SIMULATION RESULTS AND DISCUSSION

In this section,we present numerical outage probability results of the proposed CQEMRB schemes.In the numerical evaluation,we consider that fading amplitudes of all the source-relay channels and relay-destination channels (i.e.,|hsi|2and|hid|2)are independent exponentially distributed with a mean ofMoreover,an SNR ofγs=20dB,a channel bandwidth ofBc=100kHz,a coherence time ofTc=1ms,a data rate ofR=200kbits/s,the number of relaysM=6,and the number of quantization bits per channelNc=12,unless otherwise mentioned.

Figure 2 shows outage probability versus SNRγsof the conventional direct transmission and proposed CQE-MRB schemes for different data rates ofR=150kbits/s and 200kb its/s.It can be seen from figure 2 that the outage probability of direct transmission is initially lower than that of CQE-MRB scheme in the low SNR region,which is due to the fact that compared to the direct transmission,an additional factor 1/2 is used in (3)and (10)for the CQE-MRB scheme since two orthogonal channels are needed for completing the signal transmission from the source to destination via relays.However,as the SNR increases,the outage probability of proposed CQE-MRB scheme decreases significantly and then becomes better than that of direct transmission scheme in the high SNR region.Figure 2 also illustrates that as the data rate increases fromRk=150 bits/s to 200 bits/sk,the outage probability of CQE-MRB scheme increases,implying the throughput improvement at the cost of a degradation of the transmission reliability.This is because that an increase of the data rate decreases the possibility of succeeding in decoding the source signal at the destination with a certain level of effective throughput

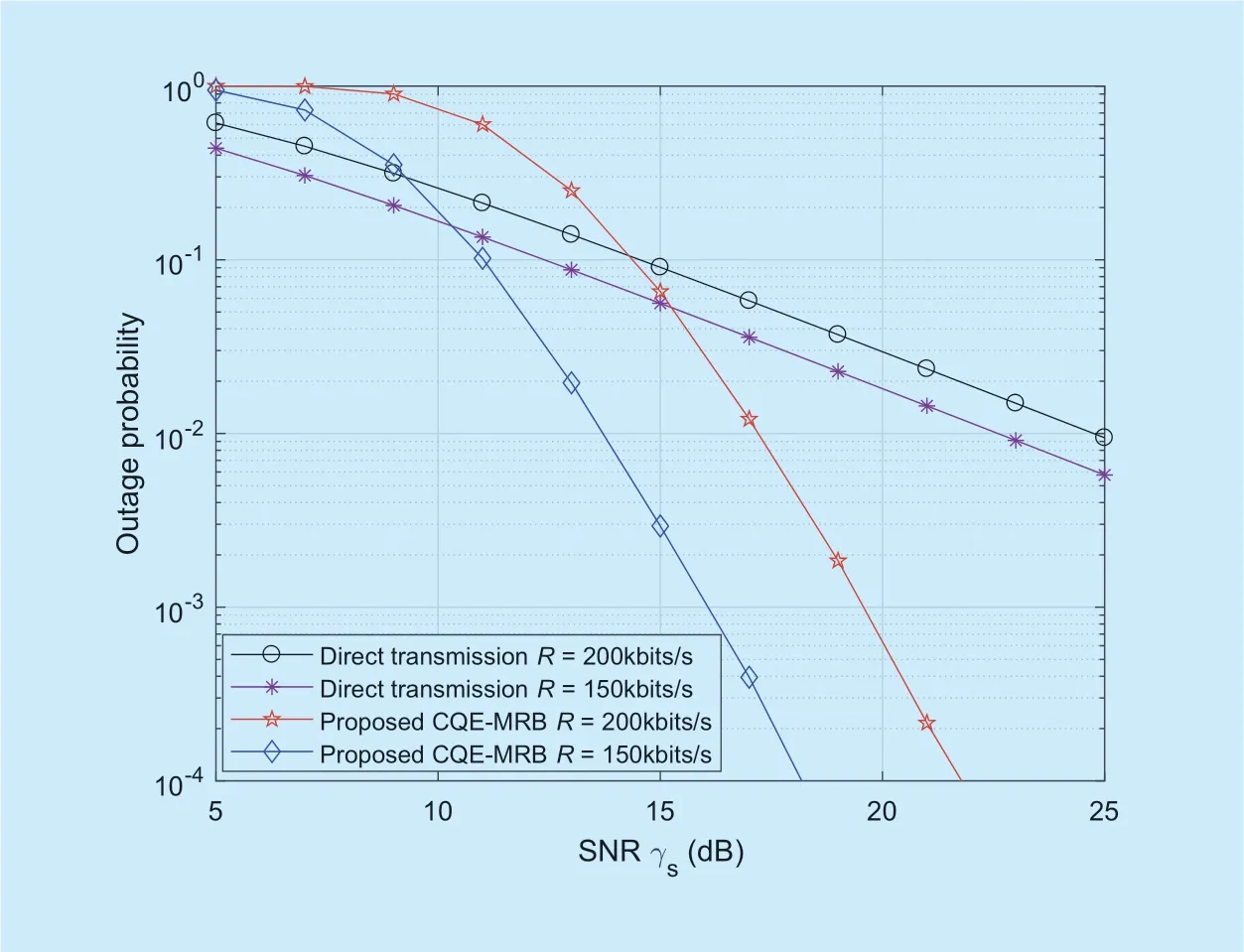
Fig.2.Outage probability versus SNR γsof the conventional direct transmission and CQE-MRB schemes for different data rates.

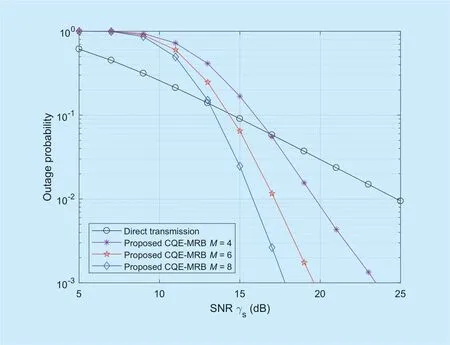
Fig.3.Outage probability versus SNR γsof the conventional direct transmission and CQE-MRB schemes for different number of relays.

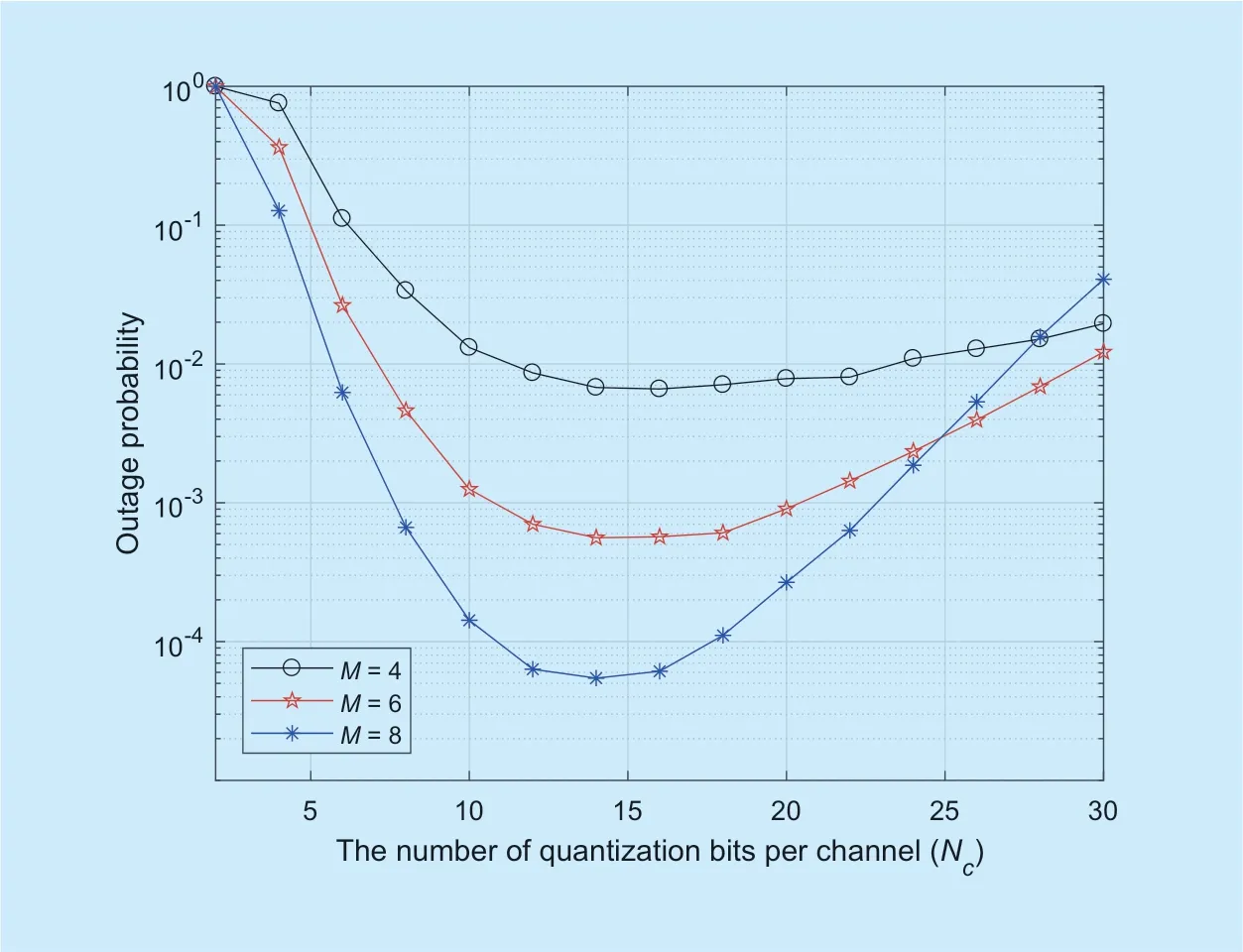
Fig.5.Outage probability versus the number of quantization bits per channel Ncof the CQE-MRB scheme for different number of relays.

Figure 3 shows outage probability versus SNRγsof the CQE-MRB scheme for different number of relaysM=4,6 and 8.One can observe from figure 3 that the outage probabilities of conventional direct transmission and CQE-MRB schemes decrease with an increasing SNR.Moreover,as the number of relays increases fromM=4 to 8,the outage probability of CQE-MRB scheme decreases substantially.Moreover,the outage advantage of proposed CQE-MRB over conventional direct transmission becomes more significant.

In figure 4,we show outage probability versus the number of quantization bits per channelNcof the CQE-MRB scheme for different data rates ofRk=200 bits/s,250 bits/skand 300 bits/sk.It can be observed from figure 4 that as the number of quantization bits per channelNcincreases,the outage probability of CQE-MRB scheme initially decreases to the minimum and then starts to increase after a critical number of quantization bits per channel.This is due to the fact that increasing the number of quantization bits per channel improves the accuracy of quantized CSIs of relay-destination channels,resulting in an enhanced effective throughput of relay-destination transmissions along with a decreased outage probability.However,it comes at the cost of an increased feedback overhead,which dominates a decrease of the effective throughput of relay-destination transmissions after a sufficiently high number of quantization bits,leading to an increased outage probability of CQE-MRB scheme.

Figure 5 shows outage probability versus the number of quantization bits per channelNcof the CQE-MRB scheme for different number of relaysM=4,6 and 8.It is observed from figure 5 that for all the cases ofM=4,6 and 8,the outage probability of CQE-MEB scheme first improves and then degrades,as the number of quantization bits per channelNcincreases.This implies that there exists an optimal number of quantization bits per channel for minimizing the outage probability of CQEMRB scheme.Additionally,as the number of relays increases fromM=4 to 8,the outage probability of CQE-MRB scheme decreases accordingly,implying the outage performance benefit of using more relay nodes.

V.CONCLUSION

In this paper,we studied the outage performance of a cooperative wireless network consisting of a source and a destination with the help of multiple relays with limited feedback in the face of channel quantization errors (CQE).We proposed a CQE oriented multi-relay beamforming (MRB)scheme,called CQEMRB,to mitigate the adverse effect of CQE on an outage performance of the cooperative network.We defined an effective throughput of relay-destination transmissions as the difference between the maximum data rate and feedback rate,which is used to evaluate an outage probability of the source-destination transmission relying on our CQE-MRB scheme.Simulation results demonstrated that the outage probability of CQE-MRB scheme can be significantly reduced with an increasing number of relay nodes.It was also shown that the outage performance of CQE-MRB scheme can be optimized through adjusting the number of quantization bits per channel.

ACKNOWLEDGEMENTS

This work was partially supported by the National Natural Science Foundation of China (Grant Nos.61522109,61631020,61671253 and 91738201)and the Natural Science Foundation of Jiangsu Province (Grant Nos.BK20150040,BK20171446 and BRA2018043)