New Identity Based Proxy Re-Encryption Scheme from Lattices

Liqiang Wu,Xiaoyuan Yang,2,＊,Minqing Zhang,Longfei Liu

1 Key Lab of Network and Information Security,Engineering University of Chinese Armed Police Force,Xi'an 710086,China

2 Key Lab of Computer Network and Information Security,Xi Dian University,Xi'an 710071,China

Abstract: Identity-Based Proxy Re-Encryption (IB-PRE)allows a semi-trusted proxy to convert the ciphertext encrypted under Alice's identity into Bob's ciphertext of the same message without leaking plaintext.Lattice-based cryptography enjoys potential resistance to quantum analysis and low computational complexity.A multi-hop and unidirectional IB-PRE from lattices is presented.We split the functions of decryption and ciphertext transformation separately,and design the double private keys mechanism,where two keys are generated for each user,one key is used to decrypt the ciphertext by Pre-Image Sampling technique,and the other is used to generate the re-encryption key by Bonsai Trees technique.The generation of the re-encryption key is non-interactive and collusion resistant.Moreover,its IND-sID-CPA security over the decisional Learning With Errors (LWE)assumption under the standard model is proved.Compared with some previous IBPRE schemes from Bilinear Pairings,the format of transformed ciphertext in our scheme remains unchanged,furthermore,it can also resist quantum analysis.Compared with some existing IB-PRE schemes from lattices with similar properties,the space of the message in our scheme is a vector of length l and the encryption process remains a lower encryption blowup factor.At last,a proof-of-concept implementation is provided.

Keywords: IB-PRE; lattices; bonsai trees; collusion resistance

I.INTRODUCTION

Proxy Re-Encryption (PRE)[1] can efficiently convert the ciphertext originally intended for Alice into the ciphertext of Bob by a semi-trusted proxy.The requirement is that the proxy gains neither involved plaintext messages nor private keys of Alice or Bob.PRE schemes have many practical scenarios,including secure e-mail forwarding system,outsourced filtering of encrypted spam and digital rights management[2].Identity-Based Proxy Re-Encryption (IB-PRE)[3]extends the notion of proxy re-encryption to the identity-based setting,where Alice and Bob's public keys can be any unique strings,for example,a phone number or E-mail address.IB-PRE can dramatically ease the workload for public key certificate management due to the property of “identity matching public key”,so it is more desirable to design IB-PRE schemes than non-identity-based ones in practice.

Some important properties for IB-PRE are described in details as follows.

(1)Unidirectionality.In a unidirectional IB-PRE system,the proxy with re-encryption key can only convert ciphertext from Alice to Bob,whereas the reverse is impossible.If converting the ciphertext from Alice into Bob or from Bob to Alice is both allowed,it is called bidirectionality.

(2)Multi-hop.Multi-hop or multi-use allows performing multiple re-encryptions on a certain ciphertext without decrypting it halfway.If the ciphertext can be converted only once,it is single-hop.

(3)Collusion resistance.Even if a dishonest proxy with re-encryption keyrkAB→and a malicious delegate with his private key colludeskB,they are still unable to obtain the delegator's private keyskA,the scheme realizes collusion resistance security.

(4)Non-interactivity.It means that Alice can calculate the re-encryption key without the participation of Bob or private key generator (PKG).

More practically,it is clearly desirable to design multi-hop,unidirectional and non-interactive IB-PRE scheme,which also becomes a hot research topic for cryptographers at home and abroad.

In 2007,Greenet al.[3] put forward the concept of IB-PRE,and then constructed the first IB-PRE scheme in the random oracle model by attaching a token to the ciphertext,which was non-interactive and unidirectional.Shortly,Chuet al.[4] introduced two IB-PRE schemes in the standard model based on Waters IBE scheme[5].Shaoet al.[6] proposed a generic construction for unidirectional IBPRE,and meanwhile instantiated it from a fully secure IBE scheme in the standard model.However,the drawback of previous schemes was that the length of transformed ciphertext would grow linearly with the transformation times.To tackle this problem,Lianget al.[7] proposed a CCA secure multi-hop IB-PRE scheme with constant-size ciphertexts.

The other method to design IB-PRE schemes was interactive [8],i.e.,the re-encryption key was created by the PKG or an extra re-encryption key generator,and the resulting scheme was always single-hop.

Thus far,in the context of identity-based encryption,many existing IB-PRE schemes have been realized based on number-theoretic problems such as the Bilinear Pairings and Quadratic Residuosity assumptions.However,these schemes are unable to resist quantum attacks because of Shor algorithm [9].

To deal with the challenges from quantum-computing,it is most urgent to design cryptosystems which remain secure in post-quantum times.Cryptosystems from lattices are conjectured to resist quantum computers and hold a great promise in the post-quantum analysis.Recently,almost all the known schemes over lattices are constructed from Learning With Errors (LWE)problem[10],which not only enjoys similar average case/worst case equivalence under a quantum reduction or a classical reduction,but also provides with simple algebraic structure and almost linear operations.

It will be interesting to combine some cryptographic primitives: Lattices,Identity-Based Encryption as well as PRE,to construct IBPRE schemes under the standard model with some nice additional advantages,such as collusion resistance,multi-hop,and unidirectionality.

1.1 Related works

Recent works have focused on the development of PRE and IB-PRE schemes over lattices.The first PRE constructed from lattices was proposed by Xagawa[11],however,it was bidirectional and interactive.Aonoet al.[12]designed a key private PRE scheme and proved its CPA security in the standard model.Singhet al.[13]pointed out that Aonoet al.'s scheme [12]was not secure because the delegator's private key could be recovered if the proxy and the delegatee colluded.Kirshanovaet al.[14]proposed a new unidirectional PRE scheme over LWE,which was collusion resistant and never required any trusted third party to generate the re-encryption key.Jianget al.[15] constructed a multi-hop and unidirectional PRE scheme from the BGN-type cryptosystem.

To date,the known constructions of IBPRE schemes from LWE have been mainly limited to the three methods classified as follows.

The first method was constructing re-encryption key by the straightforward differential between Alice and Bob's private keys,which was structurally similar to some El-Gamal-based PRE schemes.The first IB-PRE scheme presented by Singhet al.[16] was typical of this kind,in which the re-encryption key was expressed byrkA→B=sk A-skB,whereskAandskBwere private keys for Alice and Bob respectively.On transformation,theskAcan remove Alice's ciphertext andskBcan be used to create new ciphertext.Obviously,the main drawback of this method is that the resulting scheme can only realize bidirectionality.

The second method to design IB-PRE schemes was employed by Bits and Power2 functions[12].These functions originally appeared in some fully homomorphic encryption schemes and played a key part in the ciphertext transformation.The Power2 is used to embed Alice's private key into re-encryption key and Bits function is used to deal with the original ciphertext.The transformation from Alice to Bob holds because of the equation Bit(u)·Power2(X)=uX∈.This method was adopted by Singhet al.[17],they claimed their IB-PRE scheme could achieve INDID-CPA under the random oracle model and collusion resistance security.However,it was shown [18] that Singhet al.'s scheme was unable to resist collusion attack,because the variant of delegator's private key participated directly in the process of generating the re-encryption key,and the noise attached was unable to hide it properly.

The third method[15] came from the BGNtype cryptosystem presented by Gentryet al.[19].The ciphertext iswhereμis a bit message from {0,1} to be encrypted andb1is a random vector also from {0,1}*.To re-encrypt the ciphertext,computewhereR1→2is the re-encryption key satisfyingIt is worth noting that the ciphertext format would be kept unchanged after repetitious transformations,and the resulting IB-PRE scheme was IND-sID-CPA secure,multi-hop and unidirectional.This construction,while quite elegant,was considerably less efficient due to only one-bit message embedded along with each random vector,in addition,the detailed security proof was not present.

1.2 Our contributions

This paper focuses on designing IB-PRE schemes with the emerging cryptographic tool of lattices.A novel IB-PRE scheme from LWE is put forward in the context of classical Agrawalet al.'s IBE scheme [20].It employs some techniques such asTrapdoor Generation Function,Left and Right Sampling AlgorithmsandBonsai Trees.To create public parameters and master secret keys,aTrapdoor Generation Functionis adopted that outputs a pair of matrices including a part of public parameters and a short basis as the corresponding trapdoor[21].Two private keys are provided for each user,which are called “Double private keys mechanism”,one key is generated byLeft and Right Sampling Algorithmswhich produce two distinct trapdoors to find the short vector.Left Samplingenables the real system to create short vectors in lattices,andRight Samplingis used in the proof.The other key is generated byBonsaiTreeswhich can delegate a short lattice basis to produce the re-encryption key without any loss of quality.

Next,we highlight our technical ideas as described above in details.

In the proposed IB-PRE scheme,the system parameters include some matricesU,A1,BandA0together with its trapdoorTA0.Furthermore,TA0is kept secret and capable of extracting the private key for a useridwith the corresponding public keyFid= (A0|A1+H(id)B)).The private keys include two parts,that areSKid=(E id,Sid),on one hand,with the help of left sampling algorithm,it generatesEidsatisfyingFid·Eid=Uused to decrypt.On the other hand,with the help of Bonsai Trees technique under the master key,it delegates a lattice trapdoorSidfor lattice Λ()Fidwhich is still short to create re-encrypting key.So,when it is time to decrypt or generate a proxy re-encryption key,the user can selectEidorSidto complete the required functions accordingly.In addition,by Bonsai Trees technique,it can ensure the generation of re-encryption key is one-way andSidwill not be leaked.Therefore,the proposed scheme can better hide the decryption keyEidand prevent the similar attack[18]to recover the delegator's private key.

Details of the double private keys mechanism are described in Figue1,which enjoys the following advantages.

(1)The first partEidcomputed by PGK has small Gaussian noise,so it could be shorter.

(2)If Alice never makes use of the proxy re-encryption function,the private keySidwill never be used all the time,and the scheme will degenerate into an identity-based encryption,so the whole system holds stronger compatibility.

(3)Different operations with different keys make the scheme more secure and simpler.

It should be noticed that despised the first partEidcan also be obtained from the second partSidby sampling technique from a functional perspective,it is still computed by PGK,not bySidin our scheme,because these small sacrifices in efficiency are worthwhile compared with the advantages gained.In fact,the length of the private key increases by onlyl/2mcompared with the single private key.Considering that the private key is stored locally,the additional cost can be neglected.

The ciphertexts are also constructed as t w o p a r t s,a n dOn performing the transformation,with a short matrixSAas a trapdoor,Alice generatesRA→B=(R1，R2)such thatFARA→B=FBand sends it to the proxy.For clarification of exposition,the relation can be expressed as

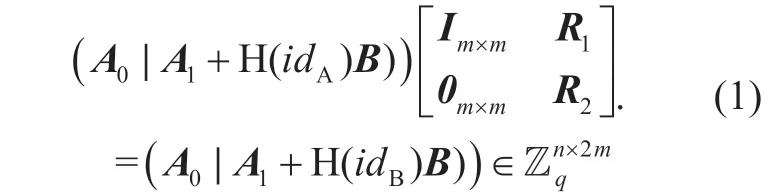
To convert the ciphertext from Alice into Bob,we just need to transform the first part of ciphertext byand the second partc2'=c2remains unchanged.

At last,its IND-sID-CPA security to the LWE problem under the standard model is presented.

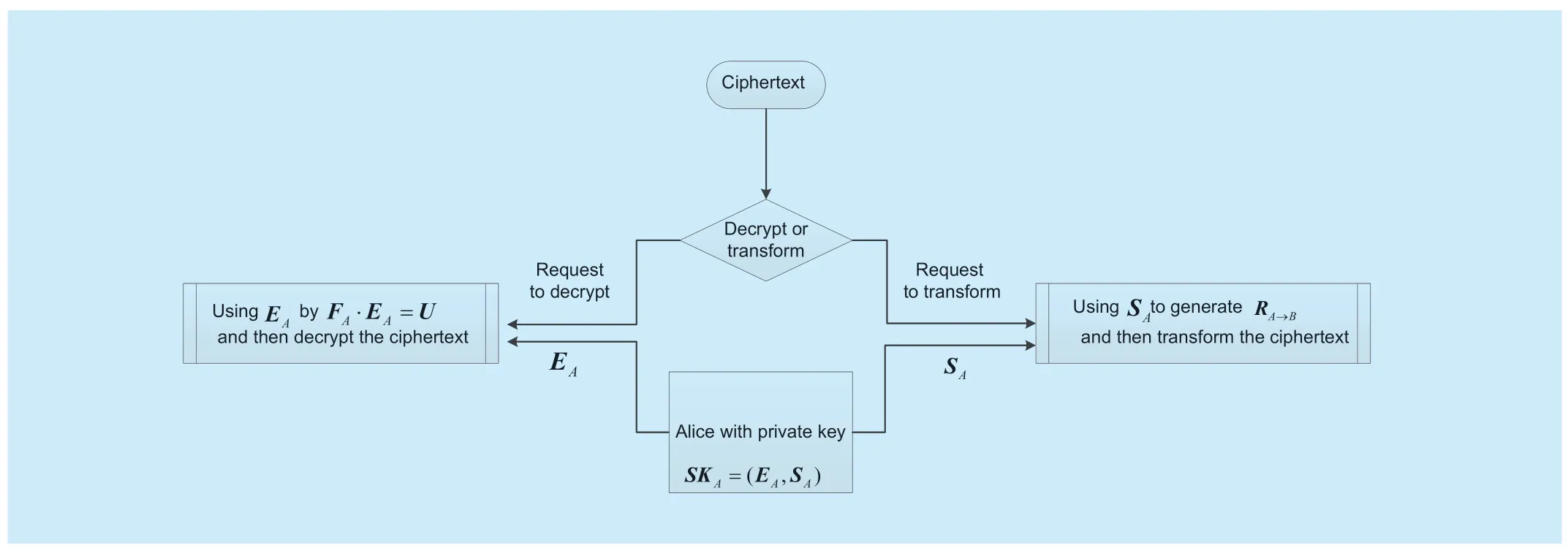
Fig.1.Double private keys mechanism.

The resulting scheme enjoys several favorable properties,such as collusion resistance,unidirectionality,and multi-hop.Compared with some previous IB-PRE schemes from Bilinear Pairings,the format of ciphertext in our scheme remains unchanged and its length will not grow linearly with the transformation times,besides,it can also resist quantum analysis.Compared with some existing IB-PRE schemes with similar properties from lattices,The space of message in our scheme is a vector of lengthleach time,not only one bit,and the encryption process enjoys a lower encryption blowup factor.

1.3 Outline

The paper is organized as follows.Section 2 provides some basic concepts,security models,and tools used for constructing our scheme; In section 3,a detailed IB-PRE scheme from LWE is described; Section 4 includes correctness analysis,strict security proof and performance comparison of related works,as well as the soft implementation; In Section 5,we take the distributed file management for example to show applications for the new scheme.At last,we give a summary of our work and discuss some open problems.

II.PRELIMINARIES

2.1 Notation

Notate the real integer and the integer number by ℝ and Z separately.Column vectors area ,b ,cand matrices are represented asA ,B ,C.The symbol [A|B] represents their horizontal connection and [A;B] for vertical connection.For a matrixS ={s1,s2…sk},||S|| denotes the longest vector inS,that is,||S| |=max||si|| forare the Gram-Schmidt orthogonalization ofis the Gram-Schmidt norm ofS.

2.2 Lattice and LWE

Lattice.Given n-dimensional linearly independent vectorsb1,b2…bm∈Zn,the integer lattice generated by the matrixB=[b1,b2… ,bm]∈Zn×mis the set of vectors

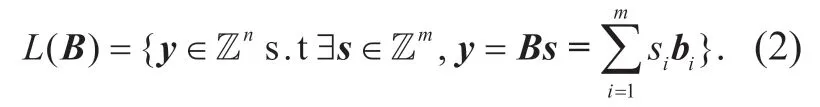
Given a primeq,a vector,and a matrixq-ar y lattices are:

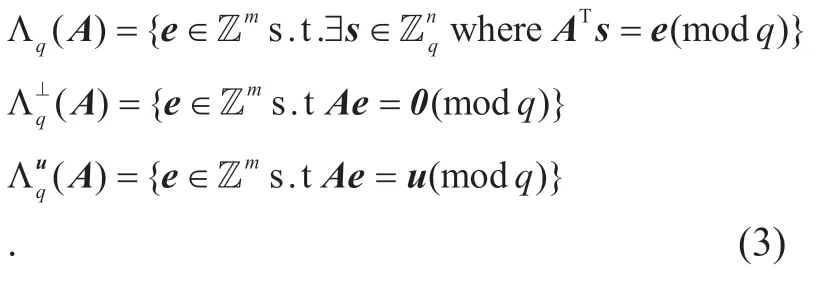
Letρs(x)be a standardn-dimensional Gaussian distribution with center 0 and any positive parameters,i.e.,ρs(x)= exp(-π||x||2/s2).For a given latticeLand a real integeris finite and computable,the lattice Gaussian distribution is notated by

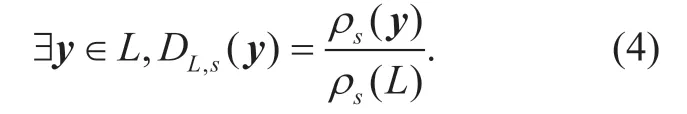
Definition1(Learning With Errors)[10].Discrete Gaussian distribution is notated byψs=DZ,s.Choose a secure parameters∈Znrandomly either from uniform or from discrete Gaussian distributionψs,then keep it secret.Given some equations with the form ofwhere the matrixis uniform at random ande∈Zmis selected according toψsm.The computational LWE problem is to recovers∈Znqexactly.

The decisional LWE is to distinguish some samples which are selected either from the distribution (or truly uniform random distributionwith an overwhelming advantage.

Theorem 1[10].Letn,qbe integers andα∈(0,1)be a real such thatIf there exists an efficient algorithm that solves LWE problem,then there will be an efficient quantum algorithm that approximates the decision version of the shortest vector problem (Gap-SVP)and the shortest independent vectors problem (SIVP)to withinO n~(/)αin the worst case.

2.3 Useful functions and algorithms

(1)Some functions from lattices.

Theorem2[20].Letq≥3,n∈Z andThe probabilistic algorithm TrapGen(q,n)produces a pairin polynomial time such thatAis a matrix in Znq×mstatistically close to uniform andTAis a short basis for lattice Λq⊥()Asatisfyingand ||TA||≤O(nlogq).

Theorem3[20].Letq≥2,with trapdoorTAbe a short basis for Λ⊥q(A)andThen foru∈Znq,there exists an algorithmSamplePre(A,TA,u,σ)that returnsx∈Λuq(A)statistically close to distributionDΛuq(A),σin polyno mial time.

Then,we describe an authorization technique with which the delegator can expand a short basis for a low-dimension lattice to any higher-dimensional extension for a delegatee's identity without any loss in quality.

Theorem4[22].LetS∈Zmm×be an arbitrary basis of Λ⊥(A)for someA∈Znq×mwhose columns generate the entire group Znq,and letbe arbitrary.There is a deterministic polynomial-time algorithmExtBa-sisthat outputs a basisS'ofsuch that

Finally,we show how to randomize a lattice basis,with a slight loss in quality.This operation is useful for delegating control to another entity securely,because the resulting basis is still short,but is statistically independent of the original basis.

Theorem5[22].With an overwhelming probability,there exists a polynomial time algorithmS'←RandBasis(S,s)such thatMoreover,for any two basesS0,S1of the same lattice and anythe outputs ofRand-Basis(S0,s)andRandBasis(S1,s)are within negl(n)statistical distance.

(2)Identity encoding function.

In our IB-PRE system,the user's identity is mapped to ann-dimensional vector in a finite field Zq.Select the polynomial field F,for a polynomialg∈F[x] of degree less thann,defined coeffs(g)to be then-vector of coefficients ofg.Ifgis of degree less thann-1,we pad the coefficients vector with zeroes on the right to make it ann-vector.Iff∈F[x] is an irreversible polynomial of degreen,then for any polynomialg∈F[x],the polynomialgm odfhas degree less thann,and therefore coeffs(gmodf)∈Fn.

Set the useridasg=(id1,id2…idn)∈Zn,and defined

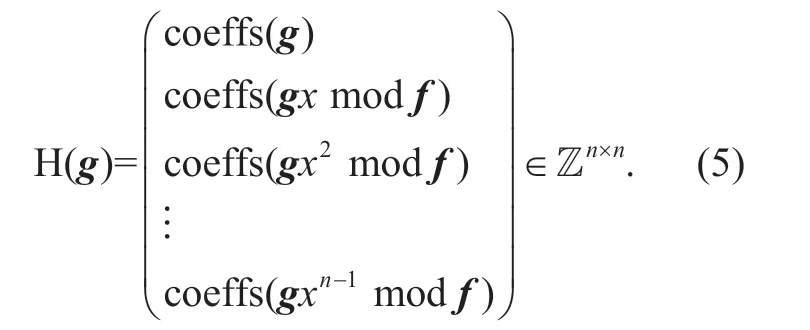
Definition 2: Assuming thatqis a prime number,nis an integer,and the identity encoding function H is defined as a differential full rank coding function [20],which has the following properties:

①For all the different identitiesg1,g2∈Znq,the matrix H(g1)- H(g2)∈Znq×nis full rank;

②Calculation ofHcan be completed in the polynomial time.

(3)Private key extraction algorithm

Algorithm 1: LeftExtract(A0,T A0,U,σ,id,A1,B).with trapdoorTA0∈Zm×msatisfying

Input: A user id,some matricesB,A1,A0

Output:Eid～DZ2m×l,σ,which satisfies

① Encode identity asFid= (A0|A1+ H(id)B))accordingly.

②Randomly chooseE1∈Zml×which is distributed toDZml×,σstatistically.

⑤ Outputid's private keyEid=(E2;E1)∈Z2m×l.

2.4 Models and security notions

Definition 3:IB-PRE includes the following six algorithms[3].

(1)Setup(1λ): On input a security parameterλ,output the public parameters PP and master secret key MSK.

(2)KeyGen(MSK,id): On input the master secret key MSK and an identityid,output the decryption keyskidfor userid.

(3)Encrypt(id,m): On input public parameters PP,an identityid,and a messagem,this algorithm outputs ciphertextcid.

(4)RKGen(id1,id2,skid1): On input a secret keyskid1and an identityid2,this algorithm outputs a re-encryption keyrkid1→id2fromid1toid2.

(5)Re-encrypt(rkid1→id2,cid1): On input a re-encryption keyrkid1→id2and a ciphertextcid1under the identityid1,output the re-encrypted ciphertextcid2for the userid2.

(6)Decrypt(skid,cid): Decrypt the ciphertextcid,then return the ⊥ or plaintextm.

Correctness: If a multi-hop and unidirectional IB-PRE scheme is correct,theDecryptalgorithm always recovers the message from ciphertext which is either generated by encrypting a plaintext usingEncrypt,or applying theRe-encryptalgorithm up to MaxLevels-1 times using valid re-encryption keys.

Suppose ∀m∈M,∀id1,id2∈{0,1}*,whereskid1=KeyGen(MSK,id1),skid2=Key-Gen (MSK,id2),rkid1→id2=RKGen(id1,id2,skid1),cid1=Re-encryptn(...,Encrypt(*,m))be a properly-generated ciphertext for ∀n＜ MaxLevels -1,the following equations hold:

①Decrypt (skid1,cid1)=m.

Definition 4.TheIND-sID-CPAsecurity[3] of an IB-PRE scheme is described with a game played between an adversary A and a challenger C.

(1)Setup.Perform Setup algorithm to obtain public parameters PP and master secret key MSK,then send PP to the adversary A.

(2)Query phase 1.The adversary A chooses some queries within next two ways.

①Extract(id): The challenger C returnsskid= KeyGen(MSK,id).

②RKGen(id1,id2): Returnskid1→id2=RKGen(id1,id2,skid1)to the adversary A,whereskid1= KeyGen(MSK,id1).

Note that adversary A is not allowed to selectid*which will be submitted in the next challenge phase such that it is possible usingExtractto extract the corresponding private key,or usingRKGento extract re-encryption key to translate fromid*to some identity else for which A holds the corresponding decryption key.

(3)Challenge phase.The adversary A selects a target identityid*and two equal length messagesm0≠m1,then presents (id*,m0,m1),and the challenger C returns= Encrypt(id*,mb)to A,whereb∈{0,1} is chosen at random.

(4)Query phase 2.A keeps on making queries as in the Query phase 1.There are some limits

①Extract(id*).

②RKGen(id*,id')and Extract(id')for any identityid' are never made before.

③RKExtract(id*,id')and consecutive calls to RKGen with initial identityid' and terminal identityid'',and last call to Extract(id'')for any identityid''.By this way,it is possible to extract re-encryption keys with the ability to translate fromid*to some identity else for which A holds the decryption key.

⑸Guess.A makes a guessb' {0,1}∈ and wins the game ifb=b'.

The advantage of the adversary A is defined as

If the AdvIAND-sID-CPA(id*)is negligible for any adversary A in polynomial time,then the IB-PRE scheme realizes IND-sID-CPA security.

III.OUR CONSTRUCTION

3.1 Setup(1λ)

On input a security parameterλ,set basic parametersn∈Z,q=ploy(n),m=O(nlogq),l=logq.Next,

⑵Select uniformly two random matrices

⑶Select a uniform random matrix

(4)Choose an H as identity encoding function.

Publish public parameters PP and keep the master key secret MSK.

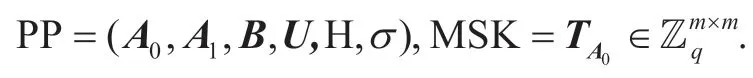
3.2 Extract(MSK,id)

(2)Compute (1)

Sid=RandBasis(ExtBasis(TA0,Fid),st)wherestis the Gaussian parameter used to generate that secret basis for users,is an upper bound on the Gram-Schmidt lengths of its secret short basis,which satisfiesFid·Sid=0.

(3)Compute

Eid =LeftExtract(A0,T A0,U,σ,id,A1,B)distributed toDZ2m×l,σ,which satisfiesFid·Eid=U.

Return the private keySKid=(Sid,Eid)to the user.

3.3 Encrypt(id,m)

(1)On input the user's identityid∈Znq,encode it as

(2)Select a uniform vectors∈Znq×1randomly.

(3)Choose a uniform matrixRid∈Zm×mfrom {-1,1} at random.

(4)Choose noise vectorsx∈ψ1s×landy∈ψ1s×m,then computez= yRid∈ψs1×m.

(5)Suppose the plaintext ism∈{0,1}l,compute

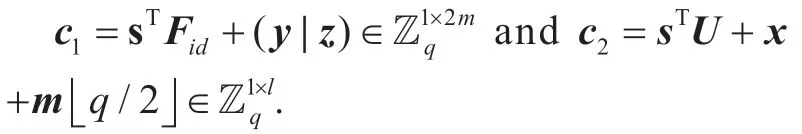
3.4 RKGen(idA,idB,SA)

Do the following steps with a part of Alice's private keysas a secret short basis for

⑴For 1≤i≤m,regard each column ofA1+ H(idB)B∈Znqasdi.Computedistributed toDΛdqi(FA),σwheresris the Gaussian parameter used to generate re-encryption key.In particular,for each column of the re-encryption key matrix,it holds thatFA·ri=di.Combine all theri(1≤i≤m） assuch thatFA·R=A1+H(idB)B.

⑵Compute the re-encryption key,and send it to the proxy

Obviously,it is easy to check

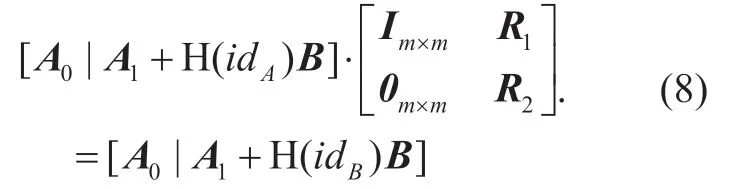
Note that the above process can be accomplished by Alice alone without interaction with user B or any trusted third party.

3.5 Re-encrypt (C A ,rk A→B)

The proxy can convert Alice's ciphertextCAto the ciphertextCBfor Bob.Here,we just need to convert the first part of ciphertext,and the second part remains unchanged.

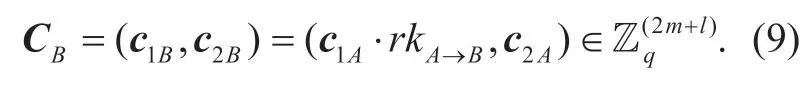
3.6 Decrypt(C,Eid)

Given the ciphertextC=(c1,c2)and a part of the private keysEid,check whether the size of the ciphertext is ||C||= 2m+lor not.If it does not hold,output symbol ⊥; otherwise,computem'=c2-c1·Eid.We parsem' as (m'1,m'2...,m'l).Fori=1,2,….l,if each entry of the vectorm'ibelongs tothenm'i= 1 elsem'i= 0.Output the plaintextm'.

The workflow of our proposed scheme can be described in Figure 2.

In the beginning,the system selects parameters and starts running (Process ①),then each user obtains its own public and private key pairs (Process ②).As for the ciphertext encrypted by a sender(Process ③),the receiver can choose to decrypt it by herself (Process ⑥),or generate the re-encryption key for the proxy (Process ④),then the proxy converts the ciphertext from Alice to Bob(Process ⑤).At last,the user Bob can continue to decrypt or transform the ciphertext in the same way.

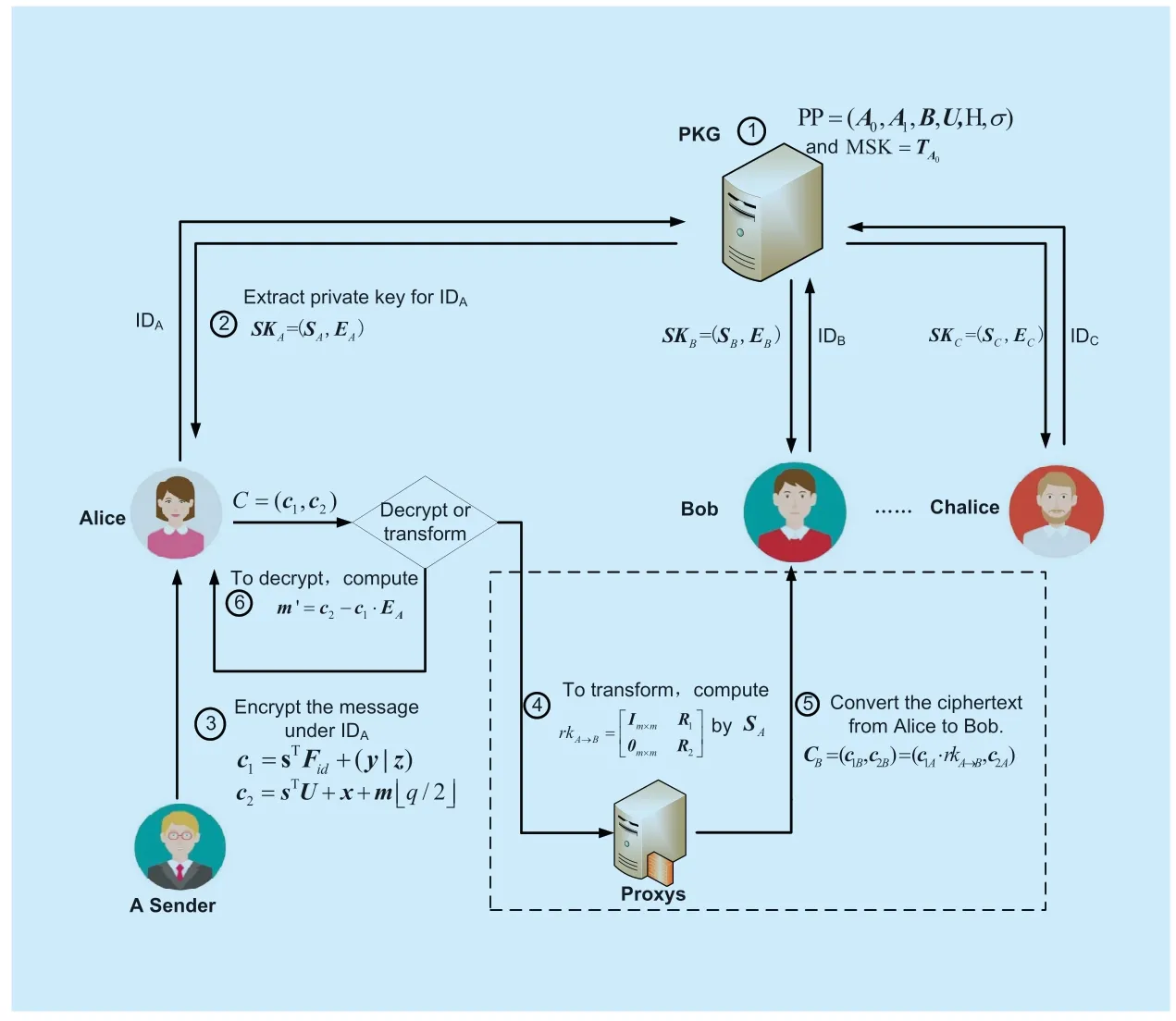
Fig.2.The workflow of our proposed scheme.

IV.ANALYSIS

4.1 Property analysis

Theorem 6 (Correctness and multi-hop).

Proof:First,for the normal ciphertext,to decrypt it byc2-c1·Eid.

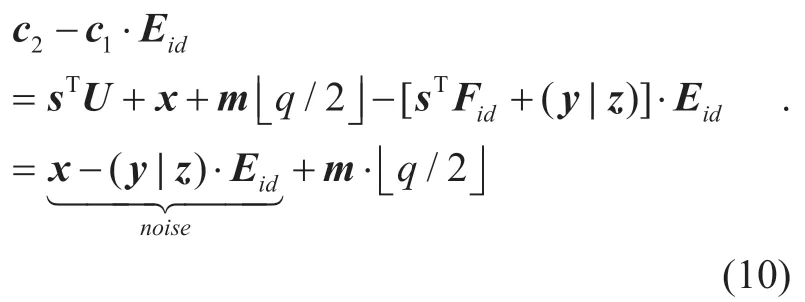
In fact,only when the noisesx- (y|z)·Eidis not bigger thancan the decryption algorithm recovermcorrectly.

Second,to decrypt the transformed ciphertext with Bob's private key,compute

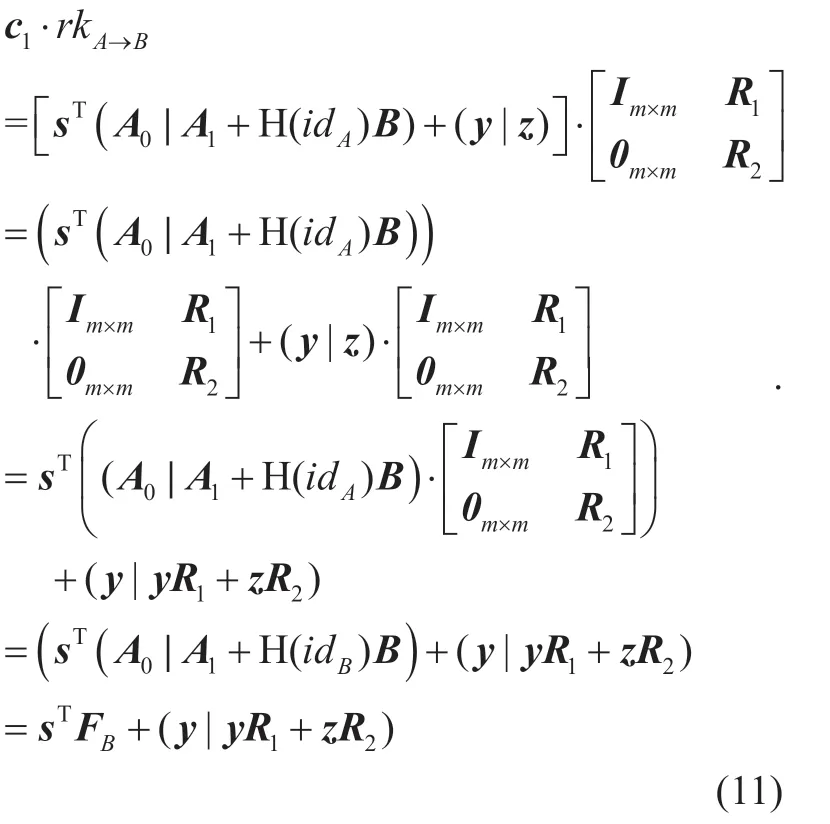
Then decrypt the ciphertext by

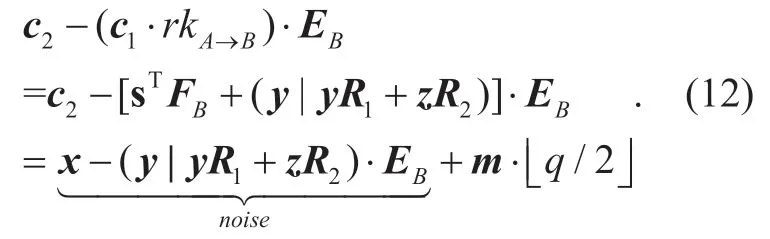
Compared to the initial noise,the new appended noises will increase with transformation times.After MAXL times of successive re-encryption,the accumulated noises will reach

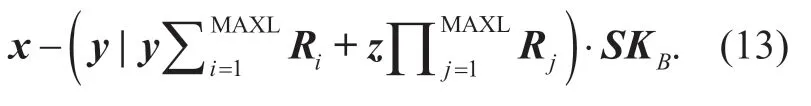
WhereRi,Rjare Gaussian noise distributed toDZmm×,sr,by restricting the noises in a certain range with proper parameter setting,the decryption is able to restore the plaintext correctly.Therefore,our scheme can realize multihop property.

Unidirectionality.Obviously,it demands the participation of the delegator's private keySAto generate re-encryption key from Alice to Bob.Thus,it cannot create the re-encryption key from Bob to others in the absence of Bob's private key.

It should be noticed that someone may still wonder whether it is feasible to invert the re-encryption keyrkAB→obtained with Alice's secret keySA.If it works,thecan transform the ciphertext intended for Bob to Alice by multiplyingrkA→B-1.

We answer this question by considering two cases because it is not sure whetherR2is invertible or not.

(1)IfR2is not full rank,andrkAB→is not invertible,thenrkAB→-1cannot be obtained.

(2)IfR2is full rank,thenrkAB→is invertible,andrkAB→-1can be used to transfer the ciphertext for Bob to that for Alice.

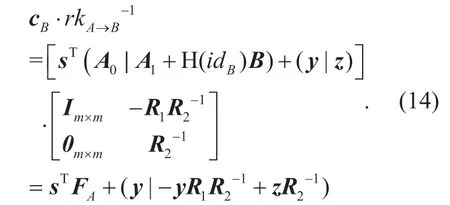
Here,the error termR2-1is uniform within [0,q-1],not as small as theR2distributed as Gaussian.Therefore the accumulated noises is too large to analyze,at last cause the decryption errors.

Collusion resistance.The property of collusion resistance security is extremely useful since even if the dishonest proxy with a re-encryption keyrkAB→and malicious delegatee with his private keyskBcollude,they are still unable to obtain the delegator's private keyskA.Generally speaking,the goal of collusion resistance is permitting Alice to delegate decryption rights,while keeping signing rights for the same public key.

At first glance,by computingSKequal=RA→B·SKB,it allows recovery of a “similar” secret key that can decrypt any ciphertext for Alice,so it seems Alice's private key is leaked completely if collusion occurred.In fact,it is not true because we might allow Bob and the proxy to recover an equivalent private key with the ability to perform delegated decryption rights,but not the same key as Alice's original private key.Furthermore,it is easy to checkand not short anymore.So,we can design a signature scheme whereSKAcan create a signature butSKequalcannot,and still keep signing rights for Alice's public key.

4.2 Security analysis

Theorem 7(Security).Assume an adversary A could win the IND-sID-CPA game,then there exists an algorithm B that solves the LWE problem with the same advantage.

Proof.We take “Game-hopping” method to prove its security.

Game sequence.

Game0: This is the real game between an adversary A and a challenger C under the original IND-sID-CPA attack model introduced in section 2.4.Assume the adversary A produces a challenge identityid*in the challenge phase.The challenger C responds by running algorithmExtractto obtain a private key for the public keyid id id()≠*and algorithmRKGento obtain a re-encryption key fromidA(idA≠id*)to other users.

Game1: The public matrixA1is not obtained at random anymore,they are computed byA1=A0R*-H(id*)Bwhere the matrixR*is randomly generated for the creation of challenge ciphertextC*.The other settings of Game1 are identical to Game0.

Game2: The challenger C does not answer the private key or re-encryption key queries by the master keyTA0,rather,it generatesBwith trapdoorTBby algorithmTrapGen,and selectsA0randomly over Znq×mwithout trapdoor.

Private key queries.It generatesSKidfor the useridby the following algorithm.

Algorithm 2: Right Extract (A0,TB,U,σ,id,A1,B)

Input: The user'sid,A0,U,σ,id,A1andBwith the trapdoorTB.

Output: Theid's partial private keyEid～DZ2m×l,σsatisfyingFid·Eid=U.

(1)Encode public key asFid=(A0|A0R*+(H(id)-H(id*))B).

(2)Construct the private key forFidas follows.

The trapdoorTBis marked asTB= (b1,b2…bm)∈Zm×m,obviously,TBis a basis of the lattice Λ⊥q(B),with the short basis,we can construct a basis for the lattice Λ⊥q(Fid).

①For 1≤i≤m,biis a column ofTB,setthenFid×t i=0.

②For 1 +m≤i≤2m,note thecias a column for the unit matrixImn,select awiso that H(id)B=A0×wi(there is no limit to the length ofwi,so it's easy to pick one satisfying the condition above),setobviously,Fid×t i=0.

(4)ComputeSid=RandBasis(TFid;st).

The resulting basisSidis still short with a slight loss in quality,but is statistically independent of the original basis.Return the private keySKid=(S id,Eid)to the user.

Re-encryption key queries:When A submits a query for re-encryption keyrkA→B,we first query private keySKA=(SA,EA)by RightExtract mentioned above,then create the re-encryption key byRKGen.

Game3: The challenge ciphertext given to adversary A is no longer generated honestly,correspondingly,it is at random completely,i.e.,C= (c1,c2)∈Z2qm+lis always chosen at random independently.

Game shift:

Game0 to Game1:The difference between Game0 and Game1 is the way to generate the matrixA1.From the view of the adversary A,it is identical by hash leftover lemma.

Lemma1 [ 20 ] : Supposemn＞ (n+ 1)log2q+ω(logn),andqis a prime number,the matricesAandBare taken from a uniform distribution,Bis am×msquare,whose value is chosen from {- 1 ,1}m×mrandomly.For any vectorw,the distribution (A,AR,RTw)is statistically indistinguishable from the distribution (A,B,RTw).

Game1 to Game2:On one hand,the private key generation process is invisible,and the obtainedEidis still statistically distributed toDZ2m×l,σsatisfyingFid·Eid=U,andSidis still statistically independently distributed toDZ2m×2m,stsatisfyingFid·Sid=0.On the other hand,the proxy re-encryption key

is indistinguishable to the Gaussian parametersr.So Game1 and Game2 are identical from the adversary's view.

Game2 to Game3: Suppose A can distinguish Game2 and Game3 with non-negligible advantage,there exists a simulator S which can solve decisional LWE with the information obtained from A.

Instance: The simulator S queries from LWE oracle form l+ instanceswhich may be either truly random distribution or a noisy pseudo-random from LWE.

Setup: The simulator S sets up public parameters:

(1)SetA0=(v1,v2,…vm).

(2)SetU=(vm+1,vm+2…vm+l).

(3)The rest of the system parameter settings are the same as Game2.

Queries: The simulator S responds to each re-encryption key query or private key query as in Game 2.

Challenge: When the adversary A sends messagesm0andm1to the simulator S,S creates the challenge ciphertext for the identityid*,where queriesExtract(id*)orRKGento translate fromid*to some identity else for which A holds a decryption key is never queried before.

(1)S e tc1' = (w1,w2…wm),w h e r ewi(1 ≤i≤m)are entries from the LWE instance.Compute

(3)Output the challenge ciphertext

(4)Simulator S choosesr' {0,1}∈ randomly.Ifr' 0= ,then the ciphertextis constructed as above,otherwise,C*is randomly chosen fromthen it sendsC*to the adversary A.

If the instances are from the LWE distribution,letthenC*is distributed precisely as in Game 3.

First,sinceFid*=(A0|A0R*),then

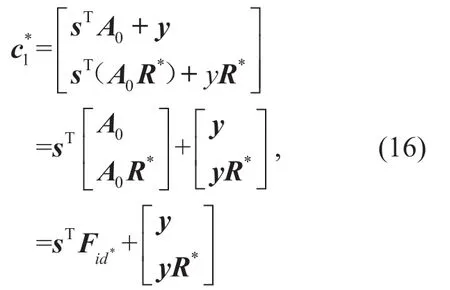
which is exactly identical to the first part of a valid challenge ciphertext as Game3.Second,notewhich is exactly identical to the second part of a valid challenge ciphertext as Game 2.

If the instances are from truly random,we have thatare uniform,which is identical to the distribution of the challenge ciphertext as Game 3.

Guess: After some additional queries,adversary A decides which Game he is interacting with,the simulator S outputs a flag for distinguishing the instances from LWE distribution or truly random by simulating views of A.

If the adversary A can distinguish Game2 and Game3,the simulator S can solve the decisional LWE with the same probability.However,that decisional LWE is difficult.So adversary A cannot win in Game 3.Considering the Game0 to Game3,we accomplish the proof for Theorem 7.

4.3 Comparison

The comparisons between our proposed scheme and similar schemes mainly include two parts.One is a comparison with the similar schemes based on Bilinear Pairings,which is mainly concerned with functionality and security because Bilinear Pairings and lattices are two different mathematical structures and it is very hard to give a concrete,“apples-to-apples” comparison of lattice-based and pairing-based IB-PRE schemes.The other is a comparison with the existing IB-PRE schemes based on LWE,we mainly focus on functionality and efficiency.The detailed comparisons include the following items.

Interactivity: To obtain re-encryption key,whether the user A needs a trusted third party or interaction with the user B or not.

Transformation times: A scheme can support multi-hop or just realize single-hop.

Directionality: Unidirectionality is that the process of re-encryption can only occur from Alice to Bob; the reverse is not available.

Collusion-resistance: A scheme can resistcollusion attacks even if the proxy conspires with the delegatee.

Security model: The scheme is constructed under the random oracle or standard model.

Message length: The length of a message encrypted each time.

Ciphertext size: The size of the resulting ciphertext after each encryption/re-encryption.

Constant-size ciphertexts: The size of ciphertext and the decryption cost is constant and will never grow linearly with the transformation times.

Computation complexity: The multiplication computation contained in each encryption/re-encryption.

Assumption: A computational hardness assumption is a hypothesis which the particular cryptographic scheme is based on,and it usually cannot be solved efficiently.

Secure in quantum:The schemes that are thought to be secure against the attack by a quantum computer.

(1)Functionality and security comparison with previous schemes from Bilinear Pairings

We choose five classical multi-hop IB-PRE schemes from Bilinear Pairings to compare with ours in terms of functionality and security in Table 1.

(2)Functionality and efficiency comparison with similar schemes from LWE

Despite identity-based PRE,multi-hop,collusion resistance,and unidirectionality all four properties have been partially or simultaneously achieved by existing schemes (In fact,only the scheme[15] can satisfy those four properties under the random oracle model),there is no efficient proposal under the standard model.Compared with the existing IBPRE scheme[15],the space of the message in our scheme is a vector of lengthleach time and the encryption process enjoys a lower encryption blowup factor,that is (2m/l+ 1)logq.The performance of all the existing IB-PRE schemes [16] [17] [15] over LWE from the following points is compared in Table 2.

4.4 Implementation

We also provide the software implementation of our IB-PRE scheme based on LWE under the standard model,which was done in C++ with the NTL and GMP libraries,referring to related works[23][24].Timings were performed on a Xeon(R)Platinum 8163 CPU with a 2.5GHz and 2GB RAM from Alibaba Cloud Elastic Compute Service.Our main goal is to show that our IB-PRE scheme can work correctly,that is to say,it is a proof-ofconcept implementation,and the efficiency may be sacrificed.

Note the security parameter as λ (classical bit security)and the lattice dimension asn.In Table3,we selectλ=80 andn=1024.Note that Extract and KenGen are time-consuming op-erations.Fortunately,they are performed only once for each participant and each delegatee respectively.As for operations of Encrypt,Re-encrypt,and Decrypt,we processlbit each time,which is quite fast and still be practical for many scenarios.

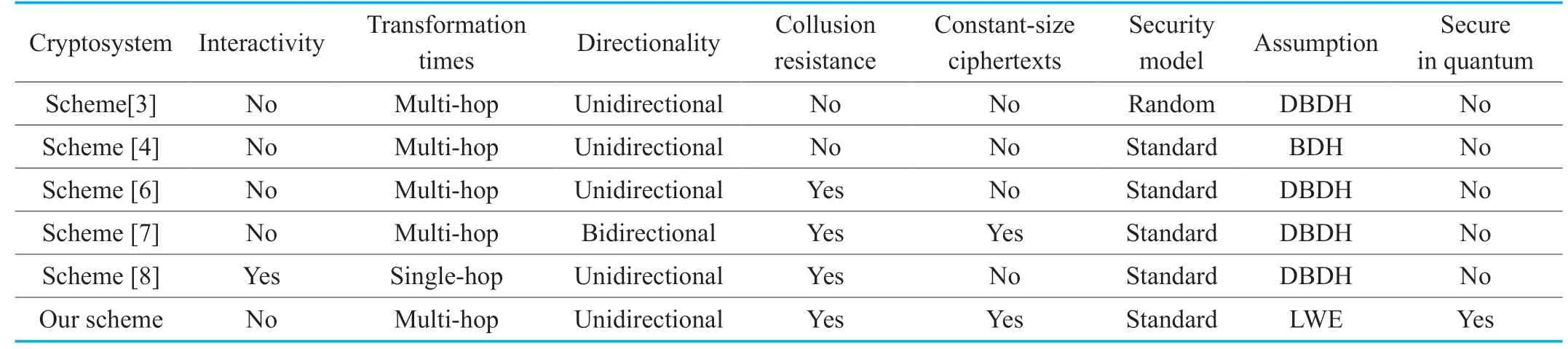
Table I.Functionality and security comparison with previous schemes from Pairings.

Table II.Functionality and efficiency comparison with similar schemes from LWE.

V.APPLICATIONS

The proposed scheme can be widely used in many scenarios such as encrypted email forwarding,access control in file management system and some computing outsourcing occasions[25][26].Next,we take the distributed file management in the cloud computing for example to show the applications of the scheme.The procedure is described in Figure 3.

Our system includes user layer,file management layer,and proxy transformation layer.In the user layer,a user first registers to get a public and private key pair,and then uploads his files to the cloud after encrypting them with his own public key.A cloud server is responsible for file storage,and the transformations of the file are performed by proxy layer.In fact,cloud server providers can act as proxy transformation layer.Now considering Alice has stored many encrypted files on the cloud,she wants to share a file with some special users such as Bob,the most efficient way is to transform encrypted files obtainable for Bob in the cloud without downloading them.The proposed IB-PRE scheme can solve this problem easily.Firstly,Alice computes a proxy key RKA-＞Bwithout any interactivity.Secondly,Alice sends the RKA-＞Bto the proxy,and then requests the proxy to transform the corresponding file for Bob.Thirdly,The proxy transforms the corresponding file with RKA-＞Bdirectly.In fact,the proxy just needs to transform thefirst part of ciphertext and the rest remains unchanged,and resulting file is also stored in the cloud and just the link is sent to Bob.At last,Bob downloads the encrypted files from the cloud and decrypts them to obtain the shared files.Although the cloud and the proxy are semi-trusted,the file is kept encrypted throughout all the circulation process,which ensures its confidentiality.The conversion of files is accomplished by the cloud,which reduces the computing load of users and embodies the advantages of cloud computing.

Table III.Timings for the different operations of IB-PRE schemes.

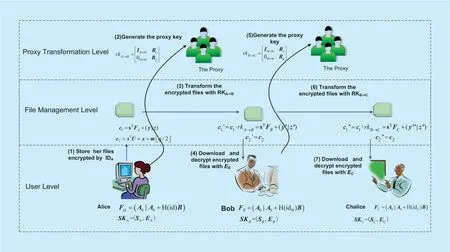
Fig.3.The file sharing system with proposed IB-PRE in the cloud.

The whole system is powerful and versatile due to abundant properties of our scheme.The potential hard assumption from lattices can resist to quantum computing attacks,therefore,the system is still secure in the post-quantum era.The unidirectionality and collusion resistance can only allow converting Alice's ciphertext to Bob's,therefore,the proxy can neither convert Bob's ciphertext to Alice at will nor obtain Alice's secret key.The multihop permits to perform a successive transformation on a ciphertext with the same method,for example,to further transform from Bob to Chalice,which solves the problem of multi-user sharing naturally.

VI.CONCLUSIONS AND OPEN PROBLEMS

An IB-PRE scheme is put forward which realizes IND-sID-CPA security under the standard model based on LWE hardness assumption.We propose the double private keys mechanism,where two private keys are generated for each user.One key is used to decrypt,and the other is used to generate the re-encryption key.On converting the ciphertext,it just needs to transform the first part of ciphertext and the second part remains unchanged.Compared with previous IB-PRE schemes,our new scheme is more efficient and simpler.Furthermore,it is unidirectional,multi-hop,non-interactive,especially can resist both quantum analysis and collusion attacks.So,it can be widely used in encrypted email forwarding and access control in the cloud system.

The next step is to further improve the efficiency of the proposed scheme.On the one hand,by using a more compact algebraic structure,such as ideal lattice,the more rapid operation speed and shorter size of ciphertext can be obtained.For example,there are also some new techniques to build compact IBE[26][28] from LWE,so it is a non-intractable work to replace our underlying IBE[20] with them to obtain a comparably efficient IBPRE to existing IBE schemes.On the other hand,by using a more efficient trapdoor generation algorithm [21] and Gauss sampling algorithm[29],the speed of generation of private keys or re-encryption keys can be improved.In addition,it is also an open problem to construct an adaptively secure IB-PRE over lattices in the standard model without sacrificing efficiency to a great extent.

ACKNOWLEDGMENTS

This research is supported by the National Natural Science Foundation of China under grant No.(U1636114,61572521,61772550),Natural Science of Shaanxi Province of China under grant No.2018JM6078,and Innovative Research Team in Engineering University of PAP (KYTD201805).