Survey on Quantum Information Security

Huanguo Zhang＊,Zhaoxu JiHouzhen WangWanqing Wu

1 Key Laboratory of Aerospace Information Security and Trusted Computing,Ministry of Education,School of Cyber Science and Engineering,Wuhan University,Wuhan 430072,China

2 School of Cyber Security and Computer,Hebei University,Baoding 071002,China

Abstract: The security of classical cryptography based on computational complexity assumptions has been severely challenged with the rapid development of quantum computers and quantum algorithms.Quantum cryptography,which offers unconditional security based on some principles of quantum mechanics,has become a significant branch and hotspot in the field of modern cryptography research.In this paper,we review the research and development of several important and well-studied branches of quantum cryptography in terms of theory and experiment,including quantum key distribution,quantum secret sharing,quantum secure direct communication,quantum signature,and quantum private query.We also briefly review the research and development of some other branches which are currently in the stage of theoretical research but receive widespread concern from academia,including quantum private comparison,quantum anonymous voting,quantum secure multi-party summation,quantum sealed-bid auction,quantum public key cryptosystem,quantum key agreement,quantum dialogue,and quantum identity authentication.In addition,we discuss some open issues and future research directions for the branches referred to above.

Keywords: quantum information; information security; quantum cryptography; quantum key distribution

I.INTRODUCTION

The 21st century is an information age.With the rapid development of information technology and related industries,information security has been playing a vital role in national security and social stability for decades [1].Information security has penetrated into all areas of national economic and social development,including politics,military affairs,medical treatment,as well as personal bank accounts,e-mail passwords,online shopping etc.However,with the emegence of various security issues,the demand for information security is becoming more and more intense,and the requirements are also getting higher and higher.

Cryptography is the theoretical basis and core technology of information security,which includes various technologies of encryption and decryption,entity authentication,message authentication etc.Cryptography consists of the symmetric cryptosystem (A.K.A.private key cryptosystem)and the asymmetric cryptosystem (A.K.A.public key cryptosystem)[2].In a symmetric cryptosystem,the encryption and decryption keys are the same,or one can be deducted from the other although there are some differences between them,while two different keys are respectively used for encryption and decryption in an asymmetric cryptosystem and it is impossible to infer the corresponding decryption key from the encryption key.The security of these cryptosystems is based on the assumption of opponents' computing power.However,with the rapid development of computer software and special hardware,especially the emergence of quantum algorithms and quantum computers,human computing power is becoming stronger and stronger,which poses a huge threat to the security.Many cryptosystems,such as the famous RSA proposed by Ron Rivest,Adi Shamir and Leonard Adleman in 1977 (“RSA” is the combination of the initial letters of their surnames),have been proved unsafe,which has aroused serious concern from all walks of life,including academia.

So far,quantum information technology has been quite mature in some areas,especially in cryptography.Quantum cryptography [3,4] is the combination of classical cryptography and quantum mechanics,which provides the first provable unconditional security for both sides of communication in principle.With the development of technology,quantum cryptography is expected to become the first commercial application of quantum communication [5].The security of quantum cryptography is guaranteed by the fundamental laws of quantum mechanics,rather than by unproven computational assumptions [4,6,7].The idea of quantum cryptography was first proposed by Wiesner in his paper entitled “Conjugated Coding” in the late 60s and early 70s [8].Wiesner showed that quantum mechanics can be used to accomplish two tasks that are impossible from the perspective of classical physics in his paper.One is to generate unforgeable bank notes,another is the use of quantum mechanics to store or transmit two messages by encoding them in two “conjugate observables” such as linear and circular polarization of light.Unfortunately,his paper was rejected by IEEE Information Theory because his idea was considered too bizarre,but was eventually published in SIGACT News in 1983.

In 1979,Charles Bennet of IBM and Gilles Brassard of the University of Montreal learned Wiesner's point of view,then began to consider the specific implementation of quantum cryptography,and proposed the first quantum key distribution scheme in 1984,which has been called BB84 ever since [3].Later,they built a complete functional prototype at IBM Thomas J.wstson Research Center in 1989.Up to now,the research on quantum cryptography has attracted much interest from researchers in the fields of theoretical and experimental physics,mathematics and computer science.Significant progress has been made both in theory and in experiment.Several companies,such as IdQuantique,MagiQ and SmartQuantum,have commercially developed quantum cryptography prototypes,which are combined with current encryption and decryption technologies to introduce quantum cryptography into practical applications.Quantum cryptography is undoubtedly a promising technology for adoption in realistic cryptographic applications,and its practical application is just around the corner.

In this paper,we first review the theoretical and experimental research and development of several important and well-studied branches in the quantum cryptography domain,including quantum key distribution,quantum secret sharing,quantum secure direct communication,quantum signature,and quantum private query,with emphasis on a number of open questions and technical issues.Then,we review the research and development of some other branches which are still at the stage of theoretical research,but have attracted wide attention,including quantum private comparison,quantum anonymous voting,quantum secure multi-party summation,quantum sealedbid auction,quantum public key cryptosystem,quantum key agreement,quantum dialogue,and quantum identity authentication.We also discuss the future challenges and research directions of these branches.For saving space,we would only like to give a brief review of some important work in each research branch,and give relevant references to the technical terms involved in this paper without making specific explanations.The organization of the remainder of this paper is as follows: We devote Sec.2 to 7 to review the research and development of the branches mentioned above,analyze the shortcomings of the research on them and look forward to the future research.In Sec.8,we provide an outlook to quantum cryptography and conclude this paper.

II.QUANTUM KEY DISTRIBUTION

Quantum key distribution (QKD)is a technology which allows two parties (commonly called Alice and Bob)to share a common key or a key sequence for encryption.In 1984,Charles Bennet and Gilles Brassard proposed the first QKD protocol,which was known as BB84 after publication.BB84 is the most famous and practical quantum cryptography protocol at present,which uses photon polarization states to transmit information.

In a QKD protocol,if an eavesdropper (conventionally called Eve)tries to steal the key,the communicators will detect her using appropriate quantum laws (e.g.the famous Heisenberg uncertainty principle).QKD is usually based on the impossibility of observing a quantum mechanics system without disturbing it.If Eve tries to eavesdrop on the quantum communication between Alice and Bob,she will inevitably leaves some traces that can be detected.Therefore,a QKD protocol achieves the following types of security: On the one hand,as long as Eve is passive (this is called robustness),the protocol generates arbitrarily long keys.On the other hand,if Eve tampers with quantum channels,the protocol identifies the attack and terminates the generation of the keys.In other words,as long as Eve is passive,the protocol will not be suspended.In addition,for any attack on quantum channels,the probability that the protocol does not stop and Eve steals the generated keys is negligible.

In the past two decades,the rapid development of QKD in theory and experiment has been reflected through a series of successful demonstrations.However,the research on QKD still faces a number of challenges,such as the distance between communicators,quantum bit error rate,and practical security etc [7,9].At present,the main research hotspots in the field of QKD include QKD networks,device-independent (DI)QKD,measurement-device-independent (MDI)QKD,detector-device-independent (DDI)QKD,security proof for QKD,and semi-QKD (SQKD).

2.1 Theoretical research

In recent years,prolific theoretical research work has been conducted,which focus on the security of QKD including the finite-key security analysis and security proof for various protocols,the design and analysis of semi,DI,MDI,DDI protocols.

2.1.1 Security of QKD

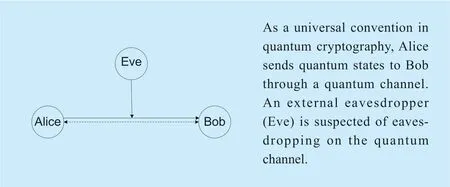
Fig.1.Generally,a quantum key distribution protocol comprises a quantum channel (the solid arrow line)and a public classical authenticated channel (the dashed arrow line).

It is known that the appeal of QKD comes mainly from the fact that it can provide unconditional security in principle.However,its security is a complex subject with several open questions still remain [10,11].Most the theoretical studies of security involve BB84 protocol.Early studies showed that,based on various assumptions,attacks against several restricted types are secure.Later,security was proved for the most general individual attacks.Since Peter W.Shor and John Preskill [12] gave the simpler proof of BB84 by relating its security to the entanglement purification protocol and the quantum error correction code,the security proof of QKD has attracted wide attention and a series of important improvements have been made.The security of two quantum cryptography schemes using d-Level Systems against individual attacks as well as coherent attacks is analyzed in Ref.[13],where the first cryptosystem uses two mutually unbiased bases,and the second exploits d 1+ mutually unbiased bases.The security proof for the protocols with entangled photons which can be applied to practical systems is presented in Ref.[14],where the proof is restricted to individual eavesdropping attacks with the assumption that the detection apparatus is trustful.Ref.[15] proposes a decoy-pulse method to overcome the photon-number-splitting attack for BB84 protocol in the presence of high loss: A legitimate user intentionally and randomly replaces signal pulses by multiphoton pulses (decoy pulses).The security proof of coherent-state protocols against arbitrary coherent attacks is provided in Ref.[16],which is based on the transmission of Gaussian-modulated coherent states and homodyne detection.Ref.[17] theoretically proves the security against the most general attacks,such as individual-particle attacks and joint attacks which can be performed on quantum channels by an eavesdropper who has unlimited technology (e.g.unlimited computing power,quantum memory and quantum computers).Ref.[18] proves the security of DI QKD against collective attacks,which is extended by Ref.[19] to a more general class of attacks.Ref.[20] provides the passive approach to the security analysis using a beam splitter to split each input pulse,and presents the complete proof of its unconditional security.Ref.[21] proves the security of BB84 with arbitrary individual imperfections simultaneously in the quantum sources and detectors.Ref.[22] provides the security bounds against coherent attacks for the protocols which use d-dimensional alphabets,and shows that the security bounds are valid in the nonasymptotic regime of finite-length keys.Ref.[23] demonstrates the semi-device-independent security of oneway QKD against individual attacks,in which the devices are noncharacterized but only assumed to produce the quantum systems of a given dimension.Ref.[24] provides the general security proof for a large class of protocols in the model where the raw key is generated by independent measurements.Ref.[25] presents the generic method to prove the security of practical distributed-phase-reference QKD against general attacks.Ref.[26] proves the security of Gaussian continuous-variable QKD with coherent states against arbitrary attacks in the finite-size regime,which is applicable in the practically relevant finite-size regime.Ref.[27] provides the strategy to prove the security of two-way QKD protocols against the most general quantum attack of an eavesdropper,which is based on an entropic uncertainty relation.Ref.[28] provides the security proof of DI QKD protocols which can be applied to generic DI QKD protocols based on arbitrary Bell inequalities,and has the same efficiency and tolerance to noise as previous proofs using memoryless devices.Ref.[29] analyzes the protocol for generating a distributed secret key from correlations that violate a Bell inequality by a sufficient amount,and proves its security against eavesdroppers under the assumption that any information accessible to them must be compatible with the non-signaling principle.Ref.[30] rigorously proves the DI QKD security of a slight variant of Ekert's original entanglement-based protocol [4] against the most general attacks.Ref.[31] presents a scheme for continuous-variable QKD using the orthogonal frequency division multiplexing technique,and gives the security analysis of the protocol with imperfect modulation.The rigorous security analysis of continuous-variable MDI QKD in a finite-size scenario is presented in Ref.[32].

In recent decade,the finite key analysis method proposed by Hayashi [33] has become a hotspot in the field of security analysis for QKD,and has been integrated into the composable unconditional security proof.Ref.[34] provides the security bounds of the finite length keys for several practical implementations of the BB84 coding,including the ones for prepare-and-measure implementations without decoy states and the ones for entanglement-based implementations which guarantee unconditional security,and the one for prepare-and-measure implementations with decoy states.Ref.[35] gives the finite-key analysis of MDI QKD,which removes all detector side channels and generates many orders of key rate higher than that of full-device-independent QKD.Ref.[36] provides the rigorous security proof against general attacks in the finite-key regime,and demonstrates the feasibility of the long-distance implementations of MDI QKD within a reasonable time frame of signal transmission.Ref.[37] proposes the practical prepare-and-measure semi-device-independent BB84 protocol with finite resources,and obtains the finite-key bound in terms of the value of dimension witnesses against collective attack for it.The finite-key security analysis which is valid against arbitrary information leakage from the state preparation process is provided by Ref.[38].

2.1.2 DI,MDI and DDI QKD

DI QKD [39] aims to narrow the gap between the theoretical analysis and the practical realization of QKD without making assumptions about the internal work of the quantum devices used.It requires the violation of the Bell inequality between Alice and Bob,and can provide higher security than traditional schemes by reducing the number of required security assumptions.In other words,Alice and Bob only need to observe the full violation of Bell inequality to prove the security.DI refers to the fact that no knowledge of the internal mechanism of the devices is necessary.In fact,the devices may be provided by an adversary.Alice and Bob regard their physical device models as “black boxes” without assuming the size of the Hilbert space of quantum signals and the type of measurements performed on them.In other words,they just need to know what elements are in their boxes,not how to implement quantum processes [40].So far,it has been proved that DI QKD can resist various attacks such as time-shift attacks [41],phase remapping attacks [42],blinding attacks [43],and wavelength-dependent attacks [44].In addition,the detection loophole caused by the losses in quantum channels can be avoided [45].The DI QKD protocol with generalized two-mode Schrodinger cat states is presented in Ref.[46].

MDI QKD,first proposed by Lo et al.in 2012 [47],is an important step to achieve the practical information theoretical security of the key sharing between remote legitimate users (Alice and Bob),in which the key is established by measuring untrustworthy relays.Compared with DI QKD,MDI QKD has several advantages.First,the key rate of MDI QKD is many orders of magnitude higher than that of DI QKD.Secondly,the detector side channels can be successfully removed.Thirdly,in a MDI QKD protocol,Alice and Bob do not need to perform any measurements,they just need to send quantum signals to be measured.Therefore,Alice and Bob do not need to hold measurement devices,and can regard the measurement devices as “black boxes” which may be completely controlled by Eve.This is important because it eliminates the need to authenticate the detectors in the QKD standardization process.Therefore,the bit strings generated by Alice and Bob will not be attacked by the detector side channel because no detectors are used.They only need to characterize the quantum states they send through the channels,and this characterization should occur in a protected environment that is not affected by an adversary,which is feasible in principle.

MDI QKD has been widely studied in recent years since its invention.Ref.[48] proposes two schemes for the phase encoding: one employs a phase locking technique with the use of non-phase-randomized coherent pulses,and the other one uses the conversion of standard BB84 phase encoding pulses into polarization modes.Ref.[49] proposes the practical protocol using phase and path or time encoding,in which the setup employs simple encoding and decoding modules without relying on polarization maintenance or optical switches.The continuous-variable MDI protocol where the detection is conducted by an untrusted third party is presented in Ref.[50].Ref.[51] presents the scheme to implement MDI protocols with the source of Gaussian-modulated coherent states,which is based on the principle of continuous-variable entanglement swapping.Ref.[52] proposes the decoy-state protocol where the measuring basis is chosen with a biased probability and the intensities of the different types of states are selected properly to optimize the achievable finite secret key rate.Ref.[53] gives the method to improve the performance of coherent-state continuous-variable MDI protocols by virtual photon subtraction via non-Gaussian postselection.Ref.[54] proposes the method to improve the performance of the continuous-variable MDI protocol by using photon subtraction,which can be implemented under current technology.Two modified MDI protocols based on the decoherence-free subspace are proposed in Ref.[55],both of two are tolerant of the fault with collective-rotation noise and collective-dephasing noise.Ref.[56] presents the protocol without vacuum source using the heralded single-photon source and global optimization,which is able to provide a high key rate and avoid the security problem caused by the vacuum source or extremely weak source.

Compared with MDI QKD,DDI QKD [57] can construct a more efficient detector sidechannel-free system,which can overcome the main shortcomings of MDI QKD.One of the drawbacks is that MDI QKD systems usually require high visibility two-photon interference between independent sources,which makes their implementation more demanding than traditional QKD systems.Secondly,MDI QKD requires larger post-processing data block sizes than standard QKD for the finite-key security bounds of general attacks.Thirdly,compared with the point-to-point QKD system,the secure key rate is significantly lower [58].In general,the security of DDI QKD is based on the following assumptions: First,the random number generator and classical post-processing of Alice and Bob are credible.Secondly,Alice's and Bob's linear optical circuits are fully characterized and cannot be affected by Eve.Thirdly,Eve can use imperfect detectors through optical fibers,but she can't access detectors and interferometers.Finally,the detectors provided by trusted providers may have some defects,which is,however,not related to Eve.In recent years,several important achievements have been made in the research of DDI QKD.Ref.[59] analyzes the security of DDI QKD and demonstrates that it is vulnerable to detector side-channel attacks as well as other side-channel attacks that exploit the imperfections of Bob's receiver,and proposes a new scheme which guarantees robustness against detector-side channel attacks in order to solve this problem.Ref.[60] analyzes the security of DDI QKD and implements the complete high-speed version clocked at 625 MHz,based on polarization encoded qubits.Ref.[61] proposes the attack method which combines the detector blind attack with the intrinsic defects of single photon detectors,and verifies the feasibility of this method through experiments.

2.1.3 SQKD

SQKD,also known as QKD with classical Bob,is a new QKD mode with the restricted quantum capabilities of at least one party,which can reduce not only the computational burden of the parties but also the cost of the quantum devices in practical implementations.SQKD allows Alice and Bob to complete the task of QKD,in which only Alice is quantum while Bob has only classical capabilities.Specifically,Alice is allowed to perform following operations:

(1)prepare any quantum states,such as Bell states,

(2)perform any quantum measurement,such as single-particle measurement and Bell measurement,and

(3)store quantum states in a quantum memory.

Bob is restricted to perform the following operations:

(1)prepare new qubits in the Z basis

(2)measure qubits in the Z basis,

(3)reorder the qubits,and

(4)send or reflect the qubits without disturbing quantum channels.

In SQKD,the party with limited quantum capacity is called classical party,and the one with full quantum ability is called quantum party.

The first SOKD protocol was proposed by Boyer et al.in 2007 in which only single photons are used and the robustness of the protocol is showed [62].Subsequently,they further extended their work by first generalizing the conditions under which the results of their work hold for the measure-resend SQKD,specifically,proved that complete robustness still holds when the qubits are sent one by one and are attacked collectively [63].Boyer et al.also proposed a experimentally feasible protocol using four-level systems instead of qubits [64].Similar to first SOKD protocol,Ref.[65] presents a protocol with classical Alice in which Alice has only classical capacities and always encodes her key bits in the Z basis.Ref.[66] proposes five SQKD protocols with complete robustness via sending less than four quantum states.Ref.[67] investigates the twoway eavesdropping strategy against a SQKD protocol.Ref.[68] presents a protocol which allows two limited classical users to establish a shared secret key with the help of a untrusted fully quantum server.Ref.[69] constructs a protocol without invoking the measurement capability of the classical party Alice and also proves it to be completely robust against quantum joint attacks,which shows that the measurement capability of the classical party is not necessary in SQKD.Ref.[70] proposes a protocol with the help of an untrusted quantum server who may try to reveal the session key of the participants through various possible attacks,in which the entanglement correlation between Bell states and Z-basis particles is used to share the session key and to detect the malicious behavior of the quantum server or eavesdroppers without invoking quantum measurement for the classical participants.In recent years,based on different quantum states and different quantum technologies,many protocols have been proposed [71-76].In addition,some work focus on to the security analysis of SQKD [77-79].

2.2 Experimental research

Since the first demonstration of QKD systems in 1992 [80],researchers have been making a lot of efforts toward the implementation of such systems with the goals of making it more practical by extending the possible communication distance and achieving the highest possible communication rate [81].After nearly 20 years of development,experimental QKD has made remarkable progress,mainly devoted to long-range communication,including fiber-based communication [82-100] and freespace communication [80,101-119].Commercial QKD systems have successfully entered the market.In short,QKD is mature enough to be used in practical applications.

2.2.1 Fiber-based QKD

At present,quantum communication networks based on optical fibers have been widely installed.In the future,the quantum channels in the global quantum communication network will mainly consist of optical fibers.The fibre-based QKD has increased the transmission distance from 32 cm [80] to 260 km [95] and the speed (or the system clock rate)from 200 Hz [80] to 10 GHz [96,97].The proofof principle experiment over 50 km of optical fibers is realized with entangled photon [98].Ref.[99] implements the differential phase shift protocol where the keys are generated at the practical rate of 166 bit/s over 100 km of fibers,which is based on the security analysis of the protocol against all general individual attacks,including photon number splitting attacks,beam-splitter,intercept-resend and photon number splitting attacks.Ref.[97] realizes the experiment over 42.1 dB channel loss and 200 km of distance with dispersion-shifted fiber.Ref.[100] implements the experiment over 250 km of distance with 42.6 dB channel loss with ultra-low-loss fiber.The experiment over 260 km with 52.9 dB channel loss is realized in Ref.[95].

2.2.2 Free-space-based QKD

Free-space connections will allow remote legitimate parties to quickly build up connections with direct line-of-sight [80,103-107,109-119].Additionally,orbital-free space links,such as satellite-to-ground links and inter-satellite links,can achieve the effective global interconnection of regional quantum networks [111,112].The expected attenuation of satellite single link grounding connections is at least 30 dB,and its feasibility has been proved in the first ground test [103,108].Ref.[108] realizes the experimental implementation of BB84 type QKD over a 144 km freespace link using weak coherent laser pulses.Ref.[113] experimentally studies the important advantage of entanglement-based QKD systems by implementing different setups on a 144 km free-space link between the two Canary Islands of La Palma and Tenerife,which can tolerate higher channel losses than the systems based on weak coherent laser pulses.Ref.[114] experimentally demonstrates the feasibility of reference frame independent QKD over a free-space link in a prepare and measure scheme using polarization encoding.Ref.[115] reports three independent experiments with a decoy-state QKD system,which addresses wide ranges of all leading parameters relevant to low Earth orbit satellites,and which paves the way towards ground-satellite QKD and a global quantum communication network.Ref.[116] proves the feasibility of BB84 QKD between an aeroplane moving at 290 km/h at a distance of 20 km and a ground station,which guarantees stable transmission of QKD signals at the single-photon level and will also significantly improve the performance of future applications of the classical communication link.Ref.[117] demonstrates quantum communication with polarization encoding from space to ground by exploiting satellite corner cube retroreflectors as quantum transmitters in orbit and the Matera Laser Ranging Observatory of the Italian Space Agency in Matera,Italy,as a quantum receiver,the scheme of which paves the way toward the implementation of a quantum communication worldwide network leveraging existing receivers.Recently,Liao et al.reported the development and launch of a low-Earth-orbit satellite for implementing decoy-state QKD,which achieves a kilohertz key rate from the satellite to the ground over a distance of up to 1,200 km [118].In addition,they demonstrated the feasibility of satellite-based quantum communication in daylight by choosing a working wavelength of 1,550 nm and developing free-space single-mode fibre-coupling technology and ultralow-noise upconversion single-photon detectors [119].

2.2.3 QKD network

QKD network [120,121] is proposed to meet the needs of future demands for large-scale and multiuser secure communications,and provides the vision of future secure communication facilities.Ref.[122] proposes the architecture for implementing a fiber-based QKD network using optical wavelength division multiplexing in the fiber.Ref.[123] experimentally demonstrates a six-user network implemented on a bus topology,in which the network employs BB84 to transmit keys.Ref.[124] presents the scheme to build a star topology network based on wavelength division multiplexing,in which all users can exchange keys directly and simultaneously,and the insertion loss of the network is independent of the number of users.Ref.[125] reports the realization of the star topology four-user network without trusted relays,which automatically addresses the quantum signal with a quantum router and every user in the network can receive and distribute quantum keys to any others simultaneously.Ref.[126] realizes the hierarchical network with decoy state method located in Wuhu,China,operated continuously beneath the streets of the city,where seven subsidiaries of the city are connected to form a secure communication network.Ref.[127] proposes the wavelength-saving topology of a network based on passive optical elements,and reports its field test on commercial telecom optical fiber at the frequency of 20 MHz.Ref.[128] proposes a QKD network model as well as the QKD node and link for easily analyzing and understanding this network,and proposes a secret-key-aware routing method to search the optimal relaying path.

2.2.4 Experimental MDI QKD

In recent years,experimental MDI QKD has also made remarkable progress.Ref.[129] reports the experimental implementation of MDI QKD,where Alice and Bob are each connected to Charlie via independent 8.5 km spooled fiber links,as originally proposed by Lo et al [47].Ref.[130] presents the implementation of the time-bin phase-encoding MDI QKD scheme [47,49],which is immune to all hacking strategies on detection.Ref.[131] studies decoy-state MDI QKD using heralded single-photon sources,and proposes the improved method which can offer a secure transmission distance of more than 70 km.Ref.[132] proposes that MDI-QKD is highly practical and thus can be easily implemented with standard optical devices,and presents a simple analytical method with only two (general)decoy states for the finite decoy-state analysis,which can be used directly by experimentalists to demonstrate MDI-QKD.Ref.[133] proposes the phase-coding reference-frame-independent scheme which requires no phase alignment between the interferometers of two distant legitimate parties.Additionally,Ref.[133] reports the proof-of-principle experiment using Faraday-Michelson interferometers,where the experimental system worked at 1 MHz,and the average secure key rate of 8.309 bps is obtained at a fiber length of 20 km between Alice and Bob.Ref.[134] performs the field test in three adjacent sites located in Hefei City,China,via the deployed fiber network of 30 km total length achieving a 16.9 b/s secure key rate.Ref.[135] completes the implementation of MDI QKD over 404 km of ultralow-loss optical fiber and 311 km of a standard optical fiber by an optimized four-intensity decoy-state method.Ref.[136] performs the proof-of-principle experimental demonstration of plug-and-play MDI QKD over an asymmetric channel setting with a single signal laser,in which the whole system is automatically stabilized in spectrum,polarization,arrival time,and phase reference.Ref.[137] takes the modulation error into consideration and presents the experiment with state preparation imperfections over the fiber links of 40 km.

2.3 Problems and challenges

Despite the rapid progress in theoretical and experimental research in recent years,the research of QKD still faces many challenges.On the one hand,almost all the hypotheses about the current security proof of QKD are crucial.However,in practical applications,these hypotheses are difficult to prove correct,because quantum devices always have a number of defects,such as detector's back-door pulse and dead-time [43,138-140].Therefore,a proof with weaker hypotheses remains the subject of ongoing research.On the other hand,a practical QKD system still faces many challenges,such as the inefficiency of classical communication authentication,the limited size effect of data processing,the defects of significant setup,the fidelity of quantum states under the influence of quantum noise,and the lack of commercial use of entanglement in commercially available QKD systems.Especially the secret bit rate is usually very low,which is the main obstacle to metropolitan QKD networks.DI QKD can overcome the device imperfections that may lead to the existence of some security loopholes which enables an eavesdropper to acquire the secret key of the practical QKD system if quantum hacking strategies are smartly designed.Unfortunately,almost all DI QKD schemes impose strict restrictions on the specifications required for physical devices,such as the need for loophole-free Bell testing,which makes them challenging and difficult to implement with current technologies.In this case,a number of MDI QKD protocols are proposed in order to relax these constraints with the main additional assumption that the source used is trustful.However,MDI QKD still faces enormous difficulties and challenges.On the one hand,compared with standard point-to-point (PTP)QKD,the implementation of MDI QKD is more difficult.On the other hand,due to the need for the two-photon interference,its technical complexity is higher than the prepare-and-measure scheme which requires that the two photons are indistinguishable in all degrees of freedom.Future research should consider how to solve above problems.

III.QUANTUM SECRET SHARING

Secret sharing is an important cryptographic primitive in the field of secure multi-party computation,and it can be regarded as a special case of secure multi-party computation.It includes the method of dividing messages using mathematical algorithms and assigning shares to two or more legitimate users through classical communication.Only when a sufficient number of parties cooperate with each other by sharing their secret parts can they reconstruct the secret.Secret sharing has applications in password-authenticated key agreement,hardware security module,electronic voting,cloud computing,online auction,private querying of databases,establishment of restricted access code etc.The first classical secret sharing scheme is invented independently by Shamir [141] and Blakley [142].

The original message can be reconstructed if and only if at leastk(1 ≤k≤N)shares are known.This is called (k,N)secret sharing threshold scheme (the threshold isk),which comprises the distribution of the shares of a secret or a random key amongkusers,in such a way that it can be reconstructed from at leastkshares.An example of such a secret sharing scheme is Shamir's scheme [141],which uses the concept of polynomial interpolation to generate and distribute secrets shared by a businessman,and then reconstructs them by users.Good (honest)users can successfully reconstruct secrets through cooperation,while bad (malicious)users cannot.[143].Therefore,for the successful reconstruction of a secret,at mostN k- users can be bad.

Quantum secret sharing (QSS)expands the number of legitimate users in the “traditional” QKD to more than two [144-146].Unlike classical secret sharing,the shared information in QSS can be classical or quantum.In particular,QSS is very useful for creating private keys in secure multi-party communications.QSS contains the behavior of splitting messages,which can only be retrieved through the cooperation of all receivers.In a QSS protocol,the sender named Alice distributes secret parts to two receivers named Bob and Charlie,respectively.In this way,neither Bob nor Charlie has any information about the key alone,but they have complete information together.In addition,eavesdroppers' attempts to obtain some information about the key will inevitably result in errors in data transmission,thus exposing their existence.

The first QSS scheme was proposed by Hillery et al.in 1999 by using three-particle and four-particle Greenberger-Horne-Zeilinger (GHZ)entangled states [144].Although the scheme elegantly proposes a quantum mechanics method to realize the above secret sharing function,its implementation seems to be problematic due to the difficulty in preparing GHZ states.Up to now,QSS has been extensively studied both experimentally and theoretically.Based on various quantum states and quantum technology,a lot of protocols have been proposed [145-157].In recent years,circular QSS,which is useful and efficient when one of the users is remote to the others who are adjacent,especially the number of the users are more than three,has attracted much attention and several protocols have been proposed [158-160].In addition,semi-QSS has also become a research hotspot [161-163].Moreover,several achievements have been made in the research of DDI and MDI QSS [164-166].Future research in these directions will continue and receive wider attention.

After nearly 20 years of development,quite a few important progress has been made in the research of experimental QSS,although its experimental feasibility level is far from that of QKD.Ref.[167] presents the setup for QSS based on energy-time entanglement,and demonstrates the feasibility of QSS using pseudo-GHZ states which do not consist of three down-converted photons but only of two down-converted ones plus the pump photon.Ref.[168] develops the theory of continuous-variable (2,2)threshold QSS [169] and implements it by using optical interferometry and squeezed light sources.Ref.[170] extends continuous-variable (2,2)threshold QSS [169] and presents two schemes to perform continuous variable (2,3)threshold QSS on the quadrature amplitudes of bright light beams,where the first scheme utilizes two phase sensitive optical amplifiers,and the second uses an electro-optic feedforward loop for the reconstruction of the secret.Ref.[171] presents the simple and practical protocol and its proof-of-principle experimental realization,in which a sequential single qubit communication between users is used.Ref.[172] presents the experimental realization of protocols by developing and exploiting the ultrastable high intensity source of four-photon entanglement.Ref.[173] presents the experimental demonstration of four-party quantum secret sharing via the resource of four-photon polarization-entangled states [174].Ref.[175] realizes the single qubit QSS experiment over telecommunication fibers in an interferometric setup with the phase encoding in three,four,and five-party implementations.The three and four-party implementations over 1550 nm single mode fiber networks,using a single qubit protocol with phase encoding is reported in Ref.[176].The proof-of-principle experiment of robust single-photon QSS over a single-mode fiber network in an interferometric setup using Schmid's scheme [171] with phase encoding in three and four-party implementations,is presented in Ref.[177].Ref.[178] presents the robust single-photon circular QSS experiment for three users over 50 km single mode fiber network using the single qubit protocol proposed by Deng et al [158] with phase encoding.

At present,there is still a certain gap between QSS and its classic counterpart.In particular,there are few research results on QSS with extended functions,such as more general threshold QSS,full dynamic QSS,and QSS with verification function.In addition,due to the lack of theoretical models of quantum information,the research results with quantum and classical information theory methods are not enough.In the future,more attention should be paid to these issues.

IV.QUANTUM SECURE DIRECT COMMUNICATION

Quantum secure direct communication (QSDC)is an important branch of quantum communication,which aims to send secret information directly through quantum channels without setting prior keys [179-182].Different from the two-channel (key distribution,ciphertext transmission channels)structure of general secure communication,QSDC requires only a single quantum channel,which is a fundamental change to secure communication structure.QSDC can eliminate the security loopholes associated with key distribution,key storage and management,and ciphertext transmission [183] in theory,and improve the security and instantaneity of communications by transmitting information directly over quantum channels.QSDC is also the basic cryptographic primitive for constructing other quantum communication tasks,such as quantum authentication and quantum dialogue.

Using Einstein-Podolsky-Rosen (EPR)pairs,Long et al.proposed the first QSDC protocol in 2002 [179],and then proposed a twostep protocol in 2003 [180].Since then,QSDC has become one of the research hotspots in the field of quantum communication.Nowadays,a lot of schemes based on a variety of different quantum states and techniques have been proposed.The quantum states used include hyperentangled states [184,185],single photons [186,187],Bell states [188-191],W states [192],five-particle cluster states [193],GHZ states [194-198],seven-Qubit entangled states [199],six-qubit maximally entangled states [200],non-orthogonal states [201],cluster states [202,203],pure entangled states [204],andχ-type entangled states [205] etc.The techniques used include quantum superdense coding [198,200,206-208],unitary operations [191,192],teleportation [193,201],entanglement swapping [189,194,196,209],quantum search algorithm [210],phase encryption [211],authentication [212],quantum one-time pads [181] etc.MDI QSDC has also been proposed and attracted much attention in recent years.The first MDI QSDC protocol was proposed by Zhou et al.in 2018 [183],in which sequences of EPR pairs and single photons are used.In the same year,Niu et al.proposed another protocol using EPR pairs,which eradicates the security vulnerabilities associated with the measurement device,and greatly enhances the practical security of QSDC [213].

The experimental research progress of QSDC is very fast,and some excellent research results have been obtained in recent years.In 2016,Hu et al.reported the first experimental demonstration based on the DL04 [181] protocol and equipped with single-photon frequency coding that explicitly demonstrated block transmission [214].In 2017,Zhang et al.reported the experimental proof-of-principle demonstration with state-ofthe-art atomic quantum memory,in which the polarization degrees of freedom of photons are used as information carriers,and the fidelity of entanglement decoding is verified as approximately 90% [215].In the same year,Zhu et al.reported the long-distance entanglement-based QSDC experiment,including the security test,information encoding,fiber transmission and decoding,in which the entangled photon pairs are stored in fiber coils and transferred over optical fibers of 0.5 km [216].More recently,using delay-coding technique instead of a quantum memory which is indispensable in original QSDC protocols,Sun et al.proposed a practical system scheme based on the DL04 protocol and wiretap channel theory,through which their experiment result shows that the reliable communication between two legitimate sides can be implemented [217].Qi et al.reported an experimental implementation of a practical quantum secure communication system using a protocol based on the DL04 protocol [181],where the system operates with a repetition rate of 1 MHz,and a secure information rate of 50 bps is achieved at a practical meaningful distance of 1.5 km [218].

In the past research,the diversity of QSDC protocol design is mainly studied.However,little attention is paid to the difficulties of protocol implementation,and the security analysis in noisy environment and how to effectively resist noise interference.The protocol may be theoretically secure,but it may be unsafe and difficult to implement in real environment.For example,it is difficult to prepare and manipulate some multi-particle entangled states using current techniques.Therefore,in the next step,in order to facilitate the implementation of the protocol,quantum states that are easy to prepare and manipulate,such as single photon states or Bell states,should be used as much as possible.Moreover,it is of great significance to study DI QSDC,MDI QSDC,DDI QSDC and semi-QSDC in the future.

V.QUANTUM SIGNATURE

Signature [219] is a cryptographic technology,which is widely used to verify the authenticity and integrity of messages,software or digital documents in real life.Signature is designed to provide a secure method of signing (classical)messages so that the signer can neither deny the messages nor forge recipients or possible attackers of the messages.

Crucially,in a signature scheme,the message is also transferable,which means that if a message is accepted by an honest recipient,it will also be accepted by another recipient if forwarded.Generally speaking,this property distinguishes a signature scheme from an authentication scheme,which ensures that a message is not tampered with by communicators,and which however,does not necessarily guarantee the transmission of messages.

A signature protocol has three goals:

(1)Message integrity: Messages are not changed during transmission;

(2)Message authentication: Message senders are trusted;

(3)Non-repudiation: Message senders cannot deny the creation of messages.

According to the dispute resolution mechanism,non-repudiation is related to transferability,which means that the recipient of the message can check whether it is likely to be accepted by other recipients if the message is forwarded.Informally,a signature protocol is secure if it has three attributes:

(1)Unforgeability: A message sender cannot send information successfully by pretending to be someone else.

(2)Non-repudiation: A signer should not be able to successfully deny that he sent the message signed with his signature.

(3)Transferability: If a recipient accepts the signature,he should be sure that any other recipient will accept the signature.

Unfortunately,the security of classical signature protocols depends on computational complexity assumptions such as the difficulty of finding discrete logarithms or decomposing large primes,which cannot be guaranteed with the emergence of quantum computers.This is the main motivation for developing unconditional secure signature schemes.

Quantum signature can be regarded as a generalization of classical signature protocols in quantum mechanics.It is considered to be a good choice because it can provide unconditional security.Current quantum signature protocols mainly include the following types: Arbitrated quantum signature (AQS)[220-225],quantum homomorphic signature (QHS)[226],blind quantum signature (BQS)[227-233],quantum digital signature (QDS)[234-237],quantum group signature (QGS)[238-241],and quantum proxy signature (QPS)[242].

In an AQS protocol,the signer signs the message and sends it to the recipient,then the recipient verifies the validity of the signature with the help of the arbitrator.A AQS protocol should satisfy [220]:

(1)No modifications and no forgery: Neither the recipient nor the possible attacker can change the signature or additional message after completion.And the signature must not be duplicated.

(2)No disavowals: The signer cannot successfully deny the signature and signature information,and the recipient can identify the signature.Moreover,the recipient could not successfully refuse to receive mails and signatures.

(3)Firm assignments: Each message is reassigned to a signature and cannot be separated thereafter.

(4)Quantum nature: Signatures involve pure quantum mechanical properties without a classical analog.Therefore,signatures are essentially unproductive and can not be denied or forged.

The first AQS protocol was proposed by Zeng et al.in 2002,which takes advantage of the correlation of GHZ states,various qubit operations,and a symmetrical quantum key cryptosystem [220].Similar to Zeng's scheme,Ref.[221] proposes the protocol using two-particle entangled Bell states.Two protocols with message recovery are proposed in Ref.[222],in which the signature is verified by a designated confirmer using GHZ states.The protocol with an untrusted arbitrator,which does not require a direct quantum link between any two users,is proposed in Ref.[223].Ref.[224] presents the protocol based on the chained CNOT operations,which encrypts quantum message ensemble.The protocol using insecure quantum channels,which can tolerate more noise in the quantum channels is proposed in Ref.[243].The protocols with continuous-variable quantum states are proposed in Refs.[225,244].

QDS aims to provide information-theoretic security for the unforgeability,undeniability and transferability of signatures based on the fundamental laws of quantum physics.Unforgeability means that the message is signed by a legitimate signer and has not been modified.Undeniability means that once the signer signed a message,he could not successfully deny that he had done it.Transferability means that when the honest recipient of the signature message accepts the signature,the other honest recipients will also accept it.QDS plays a vital role in many applications such as software distribution,financial transactions and e-mail.Generally,a QDS protocol has two phases,namely,the distribution phase and the message delivery phase.In the distribution phase,the sender sends quantum signatures (a series of quantum states)to the recipient.Then,in the subsequent messaging phase,the sender attaches the message he wants to send to the classical information about the corresponding quantum state sequence.The first QDS protocol was proposed by Gottesman and Chung in 2001 [234].In this protocol,a sender is allowed to sign a message so that one or more different recipients can verify the signature,and all recipients agree either that the message comes from the sender or that it has been tampered with.The protocol without quantum memory is presented in Ref.[236],which can be implemented using just linear optics and photodetectors that distinguish only between zero and nonzero photons.Ref.[237] presents two schemes which require neither quantum memory nor a multiport,and provides a security proof for the presented QDS schemes against coherent forging attacks.

BQS is a special type of QDS.For the purpose of privacy protection,the message content is disguised before it is signed.That is to say,the anonymity of the message owner can be protected to ensure privacy.In a BQS protocol,the message owner can always get the authentic signature of his message,even if the signer knows nothing about the content he signed.Moreover,the signature can neither be forged nor disavowed by malicious attackers.So far,several BQS protocols have been proposed.Ref.[231] presents the protocol based on the entanglement property of EPR pairs,which uses QKD and one-time pad to ensure the unconditional security and anonymity.Ref.[232] proposes the protocol based on the entangled GHZ states.The protocol based on Two-State Vector Formalism [245] is presented in Ref.[227],in which QKD and one-time pad are adopted to guarantee the unconditional security and signature anonymity.Ref.[229] proposes the batch proxy scheme based on three-dimensional two-particle-entangled quantum system,where a third fully trusted participant (the arbitrator and proxy)is involved.The fair protocol using single photons and hash functions is proposed in Ref.[228].The protocol with entanglement permutation encryption algorithm is proposed in Ref.[233].

In recent years,several important advances have also been made in experiments.The experimental quantum signature system based on the interference of phase-encoded coherent states of light is demonstrated in Ref.[246],which distributes quantum signatures from one sender to two receivers and prevents messages from forging and repudiation through polarization maintaining optical fiber and photons with a wavelength of 850 nm.Ref.[247] presents the first realization of QDS without quantum memory using only standard linear optical components and photodetectors.Ref.[248] reports the experimental demonstration of QDS over installed optical fiber,which uses the 90 km long differential phase shift QKD technology to achieve approximately one signed bit per second.Ref.[249] reports the realization of the experimental transmission over channel losses of up to 42.8 ± 1.2 dB in a link comprised of 90 km of installed fiber.Ref.[250] presents the experimental realization of quantum signature protocols,in which the transmission distance reaches 2 kilometers.Ref.[235] proposes the first protocol which removes the impractical assumption of authenticated quantum channels,and implements it over a distance of more than 100 km based on single-photon qubit states and phase-randomized weak coherent states.Ref.[251] experimentally signs a one-bit message through an up to 102 km optical fiber.Ref.[252] reports the experimental demonstration of a three-party MDI QDS protocol,which allows the signature of binary messages with a security level of 10-7.The proof-of-principle demonstration of QDS mediated by MDI QKD is reported in Ref.[253].The experimental demonstration of quantum signature protocols through a noisy 1.6 km free-space channel is reported in Ref.[254].Ref.[255] reports the proof-of-principle demonstration of the passive decoy-state QDS system that can avoid leaking the modulation information of decoy states,in which the transmission distance of the system can reach up to 200 km.

Although the theory and experiment of quantum signature have made rapid progress in the past two decades,there are few protocols for multi-user quantum signature,MDI quantum signature and continuous variable quantum signature,all of which deserves more attention.In addition,the research of DDI quantum signature is still blank,which deserves attention because the DDI schemes introduced in QKD have special advantages [57].What's more,existing BQS protocols fail to verify each party involved,while classical blind signature protocols can do this.The main reason is that classical signature protocols are mainly based on public key systems,while BQS protocols are mainly based on symmetric key systems,which limits the need for multi-party verification.Therefore,the multi-party verification of the protocols still needs a lot of work.Last but not least,designing protocols which can resist various quantum noises is also noteworthy.

VI.QUANTUM PRIVATE QUERY

Quantum private query (QPQ)is the quantum scheme of symmetric private information retrieval (SPIR)[256,257],while SPIR is the generalization of the problem of private information retrieval (PIR)problem [258].A QPQ protocol usually includes two legitimate users: a client (Alice)and a server (Bob).Alice wants to query an element of Bob's remote database to get the value corresponding to the query,and neither revealing which element she is interested in (user privacy)nor knowing anything else about the database (data privacy).In generally,Bob can test the amount of information published,and Alice is assumed to know the address of this element in Bob's database,and the content of it is usually a bit for the sake of simplicity [257].

In 2008,Giovannetti et al.[259] proposed the first QPQ protocol,which allows an exponential reduction in the communication and computational complexity compared with the (quantum or classical)SPIR protocols.Later,they gave a security analysis based on information-disturbance tradeoffs.Since then,QPQ has attracted widespread attention in academia,and many schemes have been proposed in recent years.Ref.[260] proposes the quantum solution to the classical PIR problem,which is more efficient in terms of communication complexity and the number of rounds in comparison with Giovannetti's scheme [259].Ref.[261] proposes the practical protocol based on QKD,where its basic security is guaranteed by the impossibility to deterministically discriminate nonorthogonal quantum states and the impossibility of superluminal communication.Ref.[262] generalizes the work of Ref.[261] and proposes the flexible protocol based on QKD,where the average number of the key bits Alice obtains can be located on any fixed value the users wanted for any database size.Likewise,based on the protocol proposed in Ref.[261],Ref.[263] proposes the multi-bit protocol which allows the retrieval of several bits in one query.The protocol based on B92 protocol is presented in [264].Ref.[265] presents the first DI QPQ protocol,which shows that the existing protocols fail to maintain the database security if the entangled states shared between the client and the server are not of a certain form.Ref.[266] proposes the DI protocol with finite number of entangled qubits.Ref.[267] proposes a two-way-four-state-QKD-based protocol to ensure the privacy of both sides of communication.The MDI QPQ protocol with qutrits is proposed in Ref.[268].Ref.[269] presents the loss-tolerant MDI protocols with single-photon sources.The strategies for resisting joint-measurement attack is presented in Refs.[270,271].

So far,the number of QPQ schemes is very small.In addition,experimental QPQ research has only achieved a few preliminary results [272,273],and there is a long way to go to make them into practice.In the future,more attention should be paid to DI,DDI,MDI protocols,protocols with better noise tolerance,protocol security proof and the security under imperfect sources.

VII.SOME OTHER BRANCHES

In fact,in addition to QKD,the research of quantum cryptography focuses on various branches of quantum secure multi-party computing,among which QSS is certainly the most widely studied.In recent years,quantum private comparison [274],quantum secure multi-party summation [275],quantum key agreement [276],quantum anonymous voting [277],quantum sealed-bid auction [278],etc.,have also received extensive attention.In what follows we first briefly survey these research branches,then introduce some problems and challenges in these branches,by which we wish that it can provide directions for future research.

7.1 Quantum private comparison

Assuming that there aren(n≥ 2)participantsP1,P2,… ,Pnand each partyPi(i∈{0,1,… ,n})has the secret dataxi,how to judge whether their datax1,x2,…,xnare the same while protecting the privacy of the data? This problem is called the “Tierce problem” [279],which is essentially a variant of the “millionaires' problem” proposed by Yao et al.in 1982 [280].Quantum private comparison (QPC),proposed by Yang et al.in 2009 [274],aims to solve the “Tierce problem” by using the laws of quantum mechanics.

Generally,a QPC protocol should satisfy the following two conditions [281]:

(1)Fairness: All participants get the comparison result simultaneously,in no particular order.

(2)Security: The secret data of each participant is confidential and unavailable to both the other participants and TP.In addition,external attackers (outside the protocol)cannot steal the data of the participants.There are two assumptions about the reliability of TP in QPC protocols [281,282]:

(1)TP is completely honest,that is,he faithfully implements the protocol; He will neither attempt to steal participants' secret data,nor conspire with dishonest participants to help them steal other participants' secret data.

(2)TP is semi-honest,that is,he faithfully implements the processes of the protocol without conspiring with any participants,but he can take any possible means to steal the participants' secret data.From the security point of view,the first assumption is not reasonable,because it is often impossible to find such a person in reality.Therefore,the second assumption is preferred in most existing QPC protocols.

In 2009,Yang et al.[274] proposed the first QPC protocol based on decoy photons and two-photon entangled Einstein-Podolsky-Rosen (EPR)pairs.Later,Chen et al.[283] proposed a new protocol based on triplet entangled GHZ states in 2010.Since then,more and more entangled states,such as GHZ states [284],χ-type states [285],cluster states [286],W states [287,288] and some others [289-293],have been exploited for designing QPC protocols.The early protocols aim to complete the equality comparison between two parties,and then extend to the multi-party situation [292-295] and size comparison [296,297].In recent years,research on QPC based on various quantum techniques has been extensively studied [298-302].In addition,there has been a considerable amount of research into the security analysis of protocols [303-322].

7.2 Quantum anonymous voting and quantum secure multi-party summation

Quantum anonymous voting (QAV)allowsn n(2)≥ to vote “yes” or “no” on some questions,or vote for some candidates [323].A tallyman who in charge of counting the votes is usually assumed to honestly follow the protocol,but if any information is available to her,she will have a look.A reliable QAV protocol should satisfy four conditions: privacy,security,verifiability,and eligibility [277].The first protocol was proposed by Vaccaro et al.in 2007 [323],where entangled states are employed to ensure that the votes are anonymous,and to allow the votes to be tallied.Later,Hillery et al.proposed the protocols where each party (voter)makes a vote through performing one of the two different operations on his(her)qubits [277,324].Since then,QAV has attracted widespread attention and a series of schemes have been proposed [325-335].

Quantum secure multi-party summation (QSMS)allowsn(n≥ 2)partiesP1,P2,…,Pnto compute a summation functionF(x1,x2,… ,xn)wherexiis the private datum ofPi.In fact,the counting process of votes is the summation process of several binary numbers in QAV protocols.From this point,Du et al.proposed the first quantum secure multi-party summation protocol based on non-orthogonal states,which allows a number to be added to an unknown number secretly [275].Since then,several protocols were proposed based on various quantum states and technology [337-343].

At present,there is not much work focused on the security analysis of QAV and QSMS,and only a few protocols have been proved unsafe [334],which however,does not mean that other protocols are secure.After all,it is extremely difficult to design a protocol that can resist all known types of attacks.

7.3 Quantum sealed-bid auction

Quantum sealed-bid auction (QSBA)was proposed by Naseri in 2009,through QSDC based on GHZ states [278].A QSBA protocol includes a number of bidders,an auctioneer who sometimes plays the role of a third party or auction host.Bidders simultaneously submit bids to an auctioneer without knowing others' bids,and the highest bidder will ultimately win the bidding.A secure QSBA protocol should meet six basic requirements [278]:

(1)Anonymity: The personal information of a bidder should be kept secret even if the bid is opened.That is,no bidder can obtain others' personal information,except the auction host.

(2)Public verifiability: The winning prices can be verified by any bidder,i.e.,every bidder should be able to verify the highest bid which is chosen by the auctioneer,and in this way to prevent the collusion attack between the malicious bidders and the dishonest auctioneer.

(3)Accountability of bidder: The auction cannot be interrupted by any dishonest bidders with fake bids without being detected.

(4)Fairness: The auctioneer cannot assist a malicious bidder in wining the auction without being found by other bidders.

(5)Non-repudiation: An bidder cannot deny the bid price she has cast,and the auction host cannot deny that he has received the bid from the bidder.

(6)Traceability: The bidder who wins the bidding can be identified after the auction.

In the past decade,several QSBA protocols have been designed since Naseri proposed the first protocol.Yang et al.demonstrated that Naseri's protocol is not secure,i.e,a dishonest bidder can obtain all bids of others through double controlled not attack or using fake entangled particles [343].The protocol with post-confirmation is proposed in Ref.[344],which is a direct application of the multi-particle superdense coding scheme to the auction problem.The protocol in which bidders encode their bids with secret order is proposed in Ref.[345].The protocols based on single photons and Bell states as the message carrier of bids are proposed in Refs.[346,347] and Ref.[348],respectively.The protocol based on four-particle cluster states is proposed in Ref.[349].Several other works focus on the protocol security [350-354].

7.4 Quantum public key cryptosystem

The concept of public key cryptography (PKC),also known as asymmetric cryptography,was proposed in the 1970s [219,355].In PKC schemes,such as RSA,ECC or Elgamal,the receiver sends a public key to the sender,and then the sender uses the key to encrypt the data sent to the receiver.The receiver can use his private key to retrieve encrypted data.The security of traditional PKC depends on the hardness of some computational problems,such as integer factorization problem,discrete logarithm problem,etc.However,most PKC schemes,such as RSA,will be broken by future quantum computers [356,357].Quantum public key cryptosystem (QPKC),as the natural extension of the concept of PKC in the QTM model,has attracted extensive attention in the field of quantum cryptography on the basis of unconditional security and the ability to detect eavesdropping.The main difference between quantum cryptography and QPKC is that the former uses at least one quantum channel and one classical channel,while the latter only uses one classical channel.

The first QPKC protocol (also known as quantum trapdoor one-way function)was proposed by Okamoto et al.in 2000,in which all parties,including senders,receivers and adversaries are modeled as quantum poly-time Turing machines.In 2009,Gao et al.proposed a scheme to construct quantum asymmetric cryptosystems with symmetric keys [358].In 2015,Parakh proposed the protocol that uses quantum entanglement to exchange arbitrary quantum bits between two parties without discarding any quantum bits during transmission [359].In the same year,the protocol using non-orthogonal states was proposed [360],in which each party retains a group of non-orthogonal particles as public keys in the key management center and their quantum states as private keys.Almost at the same time,Vlachou et al.[361] proposed the protocol based on quantum walk [362],in which the public key is given by the quantum state generated by the execution of quantum walk.Wu et al.proposed the scheme based on the difficulty of NP-complete problems [363],then they proposed another protocol based on Bell states,which encrypts messages with public keys and decrypts ciphertexts with private keys [364].

In fact,contrary to the widespread concern of PKC in the field of classical cryptography,QPKC has not attracted much attention in academia.Indeed,the role of QPKC in quantum cryptography is less important than that of QKD in terms of current research.

7.5 Quantum key agreement

Quantum key agreement (QKA)was proposed by Zhou et al.[276] in 2004,which allown(n≥ 2)distrustful partiesP1,P2,…,Pnto agree on a key or a key sequence through common quantum channels.Unlike the QKD in which one party decides the key and distributes it to the other,each party in a QKA protocol contributes to the final shared key,which cannot be determined entirely by some of them.At present,the number of parties involved in a protocol has extended from two [276,365-374] ton(n＞ 2)[375-388].In addition,many scholars also pay attention to the security of protocols [389-394].

Generally,in a QKA protocol,one of the participants,Pi(i∈{1,2,…,n})prepares a quantum state and encodes information on it.Then,he takes out part or all of the particles and sends them to the next participant.In this way,the particles eventually return toPi.It can be seen that the particles in the protocol are transmitted in a circular path,in which case however,any participant can steal the secret data of other participants by preparing fake quantum states,making the protocol face great security risks [389-394].In future research,a third party can be considered to prepare quantum states,and the distribution mode (see the first subgraph in figure 2)can be used to complete key agreement,by which there is no particle exchange between participants.

7.6 Quantum dialogue

Quantum dialogue (QD),or the so-called bidirectional QSDC,is an application of QSDC.Different from a system where Alice and Bob use two QSDC schemes to communicate (e.g.,one QSDC scheme for Alice-to-Bob communication and the other for Bob-to-Alice communication),QD refers to the two-way quantum communication,i.e.duplex communication,which is carried out simultaneously by both sides,just like the classical telephone communication.In other words,Alice and Bob's messages need to be encoded simultaneously in the same quantum channel.

The first QD protocol was proposed by Nguyen [395],which was proven to be insecure later [396].Since then,a lot of protocols were proposed,including protocols based on single photons [397-404],Bell states [405-408],GHZ states [409-411],W states [412,413],four-qubit cluster states [414,415].In addition to the design of protocols,the security of protocols has also attracted a lot of attention in recent years [416-421].Moreover,considerable efforts have been made in authenticated QD [422-425],and fault-tolerant QD [426-429].

7.7 Quantum identity authentication

The original intention of quantum identity authentication (QIA)is to verify the authenticity of the source,so as to protect the message from forgery and denial,and thus resist the attack of intermediaries [430].That is to say,Eve pretends to be Alice,and then establishes a shared key with Bob.Similarly,she pretended to be Bob and then established a shared key with Alice.Therefore,Eve can easily retrieve messages from Alice and Bob without being detected using established keys.In the past two decades,much attention has been paid to the research of QIA.Many protocols have been proposed,including the hybrid quantum authentication protocol [431,432],the quantum information authentication protocols [433,434],the protocol requiring a trusted authority [435],the protocol without entanglement [436],the multiparty simultaneous protocols [437,438],the quantum deniable authentication protocols [439,440],the protocols based on ping-pong technique [441,442],the scheme in a centralized quantum communication network [443],and the protocols based on entanglement swapping [444,445].It is noteworthy that most of the schemes are only applicable to specific quantum cryptography protocols,hence it is meaningful to study universal authentication schemes and related theories.

7.8 Problems and challenges

For the above branches of research,designing a secure and efficient protocol is still challenging.As we know,there are many known types of attacks against quantum cryptography protocols or systems.It is impossible to consider all the attacks when designing a protocol.Therefore,a protocol usually only analyze some well-known types of attacks.In addition,the processes of the protocol vary from protocol to protocol,and the tasks that participants undertake in the protocol also vary from protocol to protocol (e.g.whether participants are responsible for preparing quantum states and distributing particles to others,and different computational tasks that participants undertake).In this case,it is often not easy to take into account whether the process of the protocol and the tasks undertaken by the participants pose a potential threat to the security of the protocol.In other words,when designing a protocol,it is often difficult to grasp how external attackers and participants attack protocols.Because of this,a large number of existing protocols have proved unsafe.Moreover,despite the existing types of attacks,there may be many unknown types of attacks against protocols or cryptosystems that have not been invented.In short,designing a secure protocol is often difficult or even impossible.

It is known that cryptography research is oriented to commercial applications,hence the efficiency of protocols should be taken into account when designing protocols.From the perspective of protocol efficiency,how to make protocols more efficient under the condition of ensuring security is also challenging.At present,the common methods to ensure security are as follows:

(1)Preparing additional entangled states and using their entanglement correlation to verify the authenticity of the states,and judge whether there is eavesdropping in quantum channels.

(2)Using QKD to generate keys to encrypt data,that is,quantum one-time pad encryption.

(3)Using decoy photon technology to judge whether there is eavesdropping.

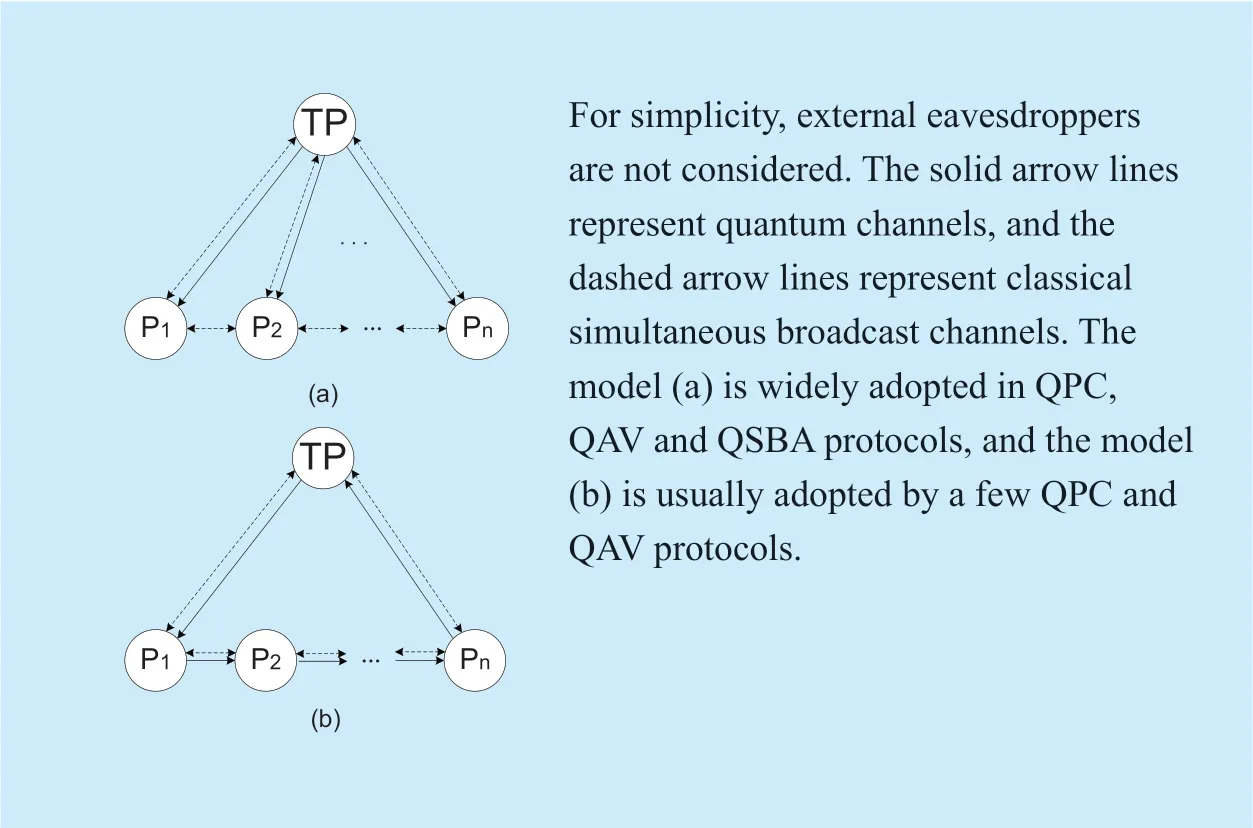
Fig.2.Two typical models of multi-party quantum cryptography protocols with a third party (here we name it TP).

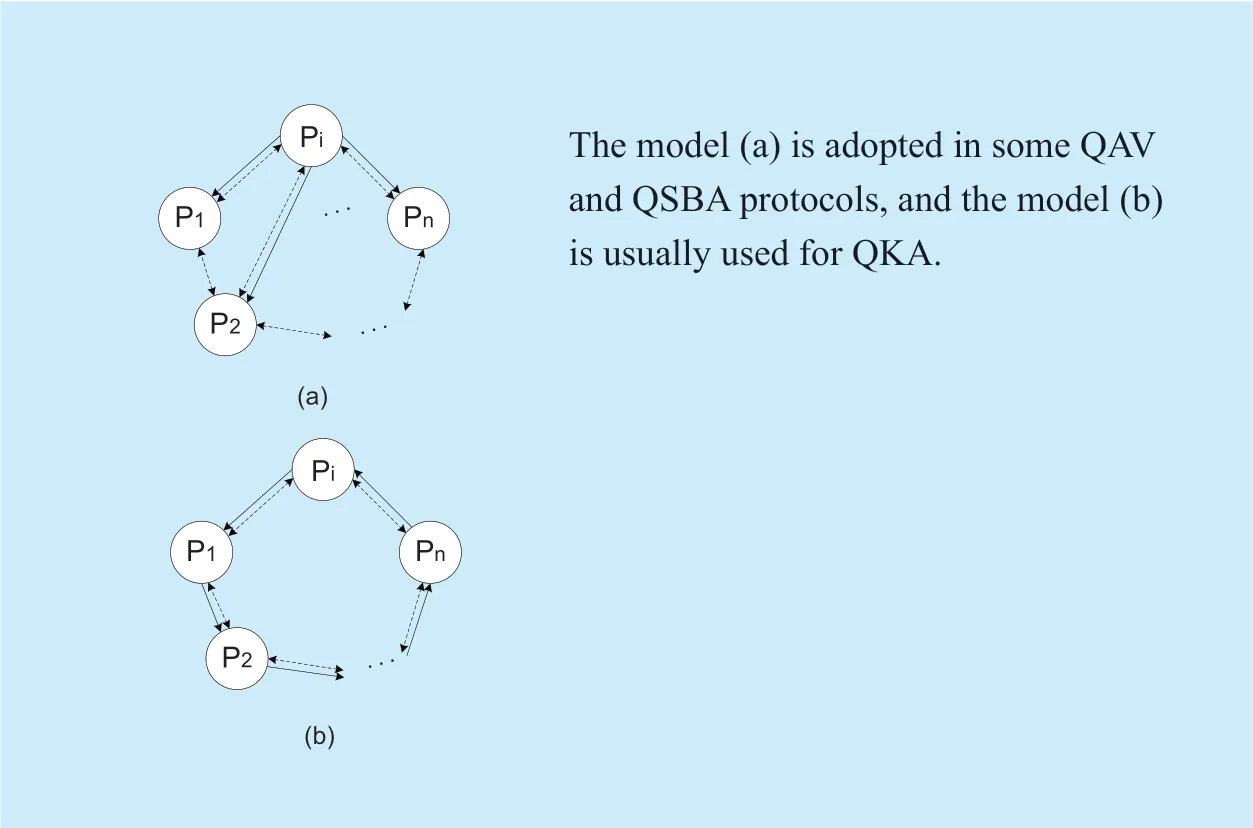
Fig.3.Two typical models of multi-party quantum cryptography protocols without a third party.

(4)Using the entanglement correlation of entangled states to protect data privacy.Generally,a protocol using the method (1)to ensure security seems more effective than other methods,because it can check the authenticity of quantum states and whether there is eavesdropping in channels.However,from the difficulty of the preparation and manipulation of entangled states,this method cannot effectively improve the efficiency of the protocol.As information carriers,multi-particle entangled states are widely used in protocol design.However,the more qubits the entangled state contains,the more difficult it is to prepare,which makes it difficult for the protocol to meet the need of high efficiency.Fortunately,with the continuous progress of related technologies,many important advances have been achieved in the preparation and manipulation of multi-particle entangled states [446-448].In the near future,the preparation of multi-particle entangled states may not be difficult.Method (2)is very effective in guaranteeing data privacy because it has been proved to be unconditionally secure.However,when both the amount of data and data value are large,this method often consumes a large number of keys,which makes the protocol difficult to meet the need of high efficiency.Method (3)is more effective than method (1)in eavesdropping checking because it is easier to prepare and manipulate a single photon than an entangled state.Method (4)often requires that the expression of a quantum state satisfy certain regularity,hence there are not many protocols designed by this method.

At present,the number of existing protocols in many branches is still very small,thus one can try to design new protocols using different quantum states (e.g.Bell states and GHZ states)in combination with different technologies (e.g.unitary operations and entanglement swapping).Generally,quantum measurement is necessary in a protocol,which is usually used to extract information carried by quantum states.In many cases,protocol design can be accomplished only by quantum measurement,such as semi-quantum cryptography protocols.In addition to measurements,the adoption of other quantum technologies will naturally increase the demand for corresponding devices and technologies.However,high qubit efficiency [449] often cannot be achieved by using quantum measurement alone,where the qubit efficiency usually determines how many states a protocol consumes.Dense coding technology is one of the effective means to improve the qubit efficiency,which has adopted by a lot of existing protocols.In addition,entanglement swapping among various quantum states has some interesting properties,which can provide new ideas and methods for protocol design.

VIII.OUTLOOK AND CONCLUSION

At present,many research branches in the field of quantum cryptography,especially in the field of QSMC,such as QPC and QKA,do not authenticate the identity of participants.In this case,any outsider can impersonate a legitimate participant to steal the participants' secret data,or send a fake message to others,which seriously threatens the security of the protocol.Thus,it is meaningful to study and design protocols with authentication processes.In addition,the noise problem has always been a widespread concern in academia.Known noise types are diverse,such as the collective dephasing noise,collective-rotation noise,unitary collective noise,decoherence noise and collective amplitude damping noise.Many branches have less research on anti-noise protocols.Therefore,the research on anti-noise protocols is still one of the hot research directions in the future.In addition,one can pay attention to classical cryptography problems and try to find those classical schemes which have not been generalized to quantum mechanics,and which bases security on the assumption of mathematical complexity,and then solve these problems by quantum mechanics methods.Moreover,the research on QKD provide a lot of valuable ideas and solutions for other branches.Using these research results,one can design safer,more efficient and more feasible protocols in experiments.For example,the research and design of DI,MDI,DDI,semi-quantum and fault-tolerant protocols are all worthy of attention.What is more,most of the branches are still at the stage of theoretical research,and there is still a long way to go before the experimental implementation of protocols.

We have reviewed the research and development of some important and well-studied branches in quantum cryptography domain theoretically and experimentally,including QKD,QSS,QSDC etc.We have also reviewed the research and development of some other research branches which are still in the theoretical stage but have attracted wide attention,including QPC,QAV,QSMS,etc.We wish that readers can obtain a general understanding of the hot research directions and progress in quantum cryptography through this paper.We also wish that this paper can provoke the interests of more researchers and carry out research work.

ACKNOWLEDGEMENTS

The authors thank the anonymous referees for their significant comments and suggestions to improve the quality of this paper.This work is partially supported by the State Key Program of National Natural Science of China No.61332019,the Major State Basic Research Development Program of China (973 Program)No.2014CB340601,the National Science Foundation of China No.61202386,61402339,the National Cryptography Development Fund No.MMJJ201701304,the Science and Technology Research Project of Hebei higher education No.QN2017020.