一种基于视觉和深度信息的山体裂缝宽度测量方法仿真研究∗

程宏浩，尚俊娜∗，施浒立

(1.杭州电子科技大学通信工程学院，杭州310018；2.中国科学院国家天文台，北京100012)

我国是滑坡灾害频发的国家，滑坡灾害往往给人民生命财产造成严重的威胁。为此国家十分重视滑坡监测的研究。滑坡裂缝的变化是滑坡的重要指标[1]，因此对于滑坡裂缝监测方法研究具有重要意义[2]。

本方法监测坡体上的土地裂缝，采用的技术属于近景摄影测量[3]的范畴，具有动态监测、无接触、自动化程度高等诸多优点[4]，已有部分学者将该技术用于滑坡监测领域。Abdallah Laribi[5]利用数字图像研究阿尔及尔滑坡不稳定区域的变化；刘文成[6]采用直接线性变换的影像系统进行滑坡监测，并对比GPS方法给出了前后的体积差为994.16 m3，测得地表相对误差为1.7%；刘志奇[7]等采用单像近景摄影技术结合SIFT特征点算法勾勒了滑坡变化区域，误差在毫米级；P.Baldi[8]等利用近景摄影技术和GPS技术研究了帕提尼奥滑坡(位于意大利北部亚平宁山脉)的演变历程；Stumpf A[9]等利用多视点摄影测量和激光扫描技术构建了滑坡体三维表面，对滑坡最不稳定的区域预估了其三维位移矢量；Mora[10]对意大利北亚平宁山脉的马耳他切坡使用近景摄影测量技术进行滑坡监测，获得了高精度数字高程模型(Digital Elevation Model，DEM)；CassonB[11]等以法国南部阿尔卑斯山的超大沙丘滑坡为例，提出了一种使用标准化图像相关技术处理监测影像进行滑坡监测的方法，测量结果与GPS测量结果一致；GPS技术是目前用于滑坡监测的一种常用方法[12-13]，目前GPS方法用于滑坡监测的精度普遍在亚厘米级(4 mm～5 mm)。

本文提出了一种基于视觉和深度信息的山体裂缝宽度测量方法，该方法首先在裂缝两侧设置圆形标志，通过检测圆形标志圆心之间的距离来反映裂缝变化，本方法具有实时观测、远程控制以及无接触等优点，实验精度可以达到2 mm。

1 理论依据

1.1 霍夫变换圆形检测

霍夫变换(Hough)是检测圆形图形的常用方法[13-14]，Hough变换检测圆[15-16]的基本思想是将图像从原图像空间变换到参数空间，在参数空间内，使用大多数边界点都满足的某种形式作为图像中曲线的描述，通过设置累加器对参数进行累积，其峰值对应的点就是所需要的信息[17-21]。

一个半径为 r0，圆心为(a0，b0)的圆，可以表示为:

假设(xi，yi)为圆上任意一点，将其投影到参数空间，可以表示为

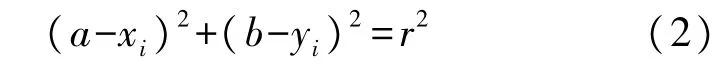
根据式(2)可以得到式(1)中任意一点(xi，yi)对应的式(2)能表达的图形，这个图形是一个圆锥形，随着(xi，yi)的改变，参数空间中的圆锥图形亦能形成多个圆锥面，多个圆锥面相交的一个点(a0，b0，r0)，就是式(1)圆中的三个参数，从而求出了相应的圆的圆心[15]。其原理示意图如图1所示。

图1 hough原理示意图

1.2 像素坐标与世界坐标的转化

从像素坐标转化到世界坐标一共涉及4个坐标系，分别为像素坐标系，图像坐标系，摄像机坐标系以及世界坐标系。

图 2为四个坐标系的示意图，其中，OWXWYWZW为世界坐标系；OC-XCYCZC为相机坐标系，光心o为原点；o-xy为图像坐标系，原点位于图像中心；u-v为像素坐标系，原点为图像左上角；P为世界坐标系中的一点，p为P在图像上的成像点，f为焦距。

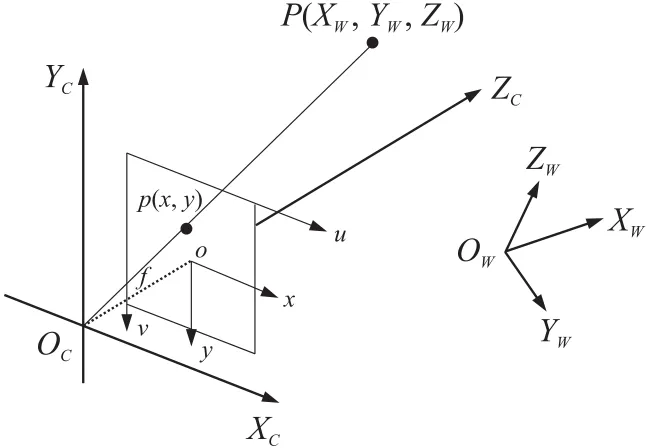
图2 四个坐标系示意图

1.2.1 世界坐标系与相机坐标系

世界坐标系是三维客观世界的绝对坐标系，也称客观坐标系，用于描述物体在三维空间环境中的具体位置。相机坐标系则是以相机的光心为坐标原点的坐标系。目标点的坐标在两个坐标系之间的转化主要是相机的旋转以及平移。

如图3所示，假设坐标系绕Z轴旋转θ，那么P点的坐标变化为:

变换为矩阵形式为:

绕y轴旋转w，可以得到

式中:R为三个坐标轴旋转矩阵的乘积，为了描述P点坐标在两坐标系间的转化，引入偏移矩阵T，偏移矩阵T描述的是摄像头的平移，这样P点在两坐标系之间的转化关系为:

1.2.2 相机坐标系与图像坐标系

从相机坐标系到图像坐标系，是从3D转换到2D，属于透视投影关系，其主要原理是利用了三角形相似的原理。

如图4所示，

图4 相机与图像坐标系

由式(9)、式(10)可以得到

根据式(13)将P点的相机坐标转换为图像坐标。

1.2.3 像素坐标系与图像坐标系

像素坐标系通常的定义方式是:原点O′位于图像左上角，u轴向右与x轴平行，v轴向下与 y轴平行。

如图5所示，像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不同，图像坐标系的单位为mm，属于物理单位，而像素坐标系的单位是像素，平常描述一个像素点都是几行几列。所以这两者之间的转换如下:

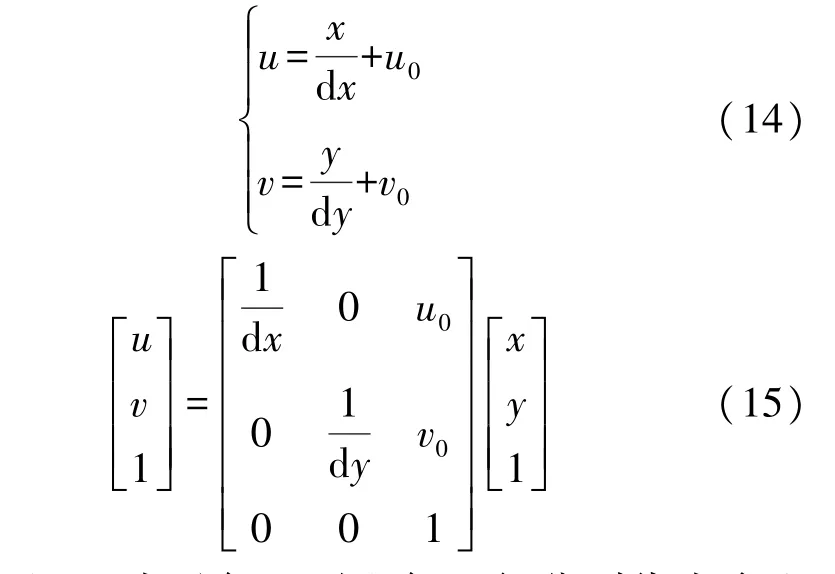
式中:dx和dy表示每一列和每一行分别代表多少mm，即1像素＝dx mm。

图5 像素与图像坐标系

上述4个坐标系之间的关系，可以将世界坐标系中任意一点转换到像素坐标系中，公式如下:

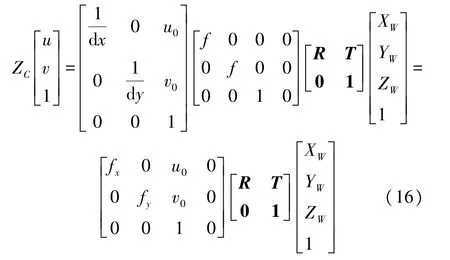
一个三维空间中点找到其在图像中对应的位置可以通过对其世界坐标依次左乘外参矩阵和内参矩阵得到。反过来已知像素坐标转换为世界坐标则必须得到其深度信息ZC。ZC可以通过深度摄像头来获取。最后根据距离式(17)求出两点的实际距离d。

2 方法流程

本方法在滑坡裂缝的两侧布置两个预先设计好的圆形标志点，通过识别圆形标志点的圆心并计算两个圆心在世界三维坐标系下的距离来反映裂缝的宽度以及深度变化，以达到对滑坡裂缝的监测。

如图6为实验装置的示意图，在坡体的稳定区域固定铁架，将相机固定于铁架上并正对滑坡裂缝，利用带圆形标志的钢钎嵌入土壤，达到与土地同步变化的效果。

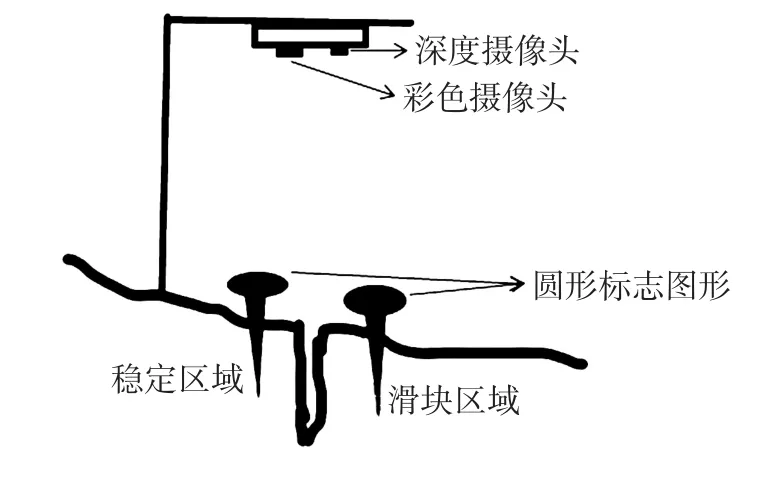
图6 实验装置示意图

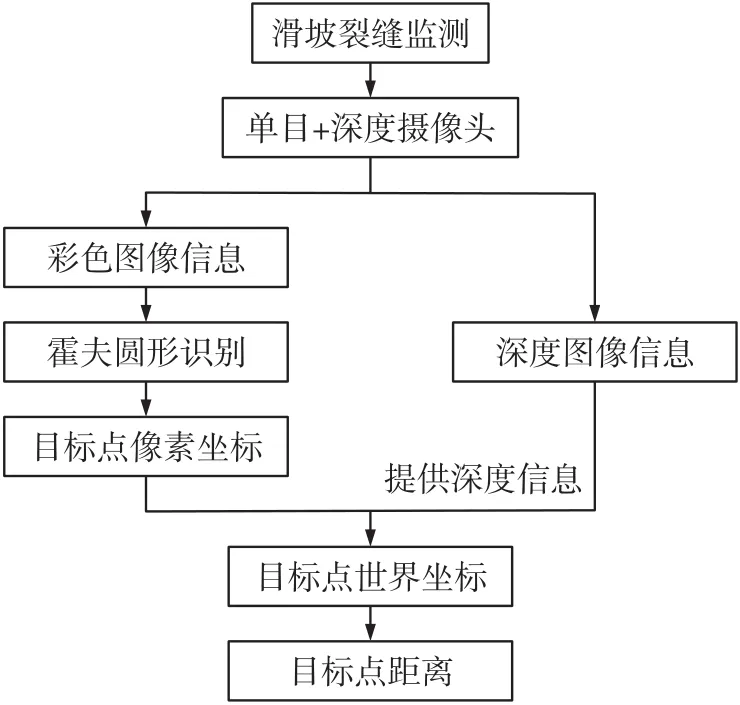
图7 方法流程图

3 实验测试

本实验摄像头设置于裂缝上方1 m处，改变标志点位置并进行多次测量。并对摄像头分别进行位移和角度的变化，探究平移以及角度变化对实验精度造成的影响。实验采用摄像头为PICO深度摄像头，型号 DCAM710，运行环境为 VS2017＋OPENCV 3.0，处理器为Intel Core i5-8400。实验装置还用到了水平仪测量摄像机角度的变化以及用摩天激光测距仪测量两个标志点的实际距离，型号M1，测量精度为2 mm。图8为深度摄像头，图9为室内实验装置图以及图10实验测试效果图。

图8 深度摄像头

图9 室内实验装置

图10 测试效果图

3.1 精度测试

实验过程中，经过多次测试后发现标志点的实际距离d和测试得到的距离ρ有偏差，实验过程中实际距离d的取值范围在200 mm～300 mm之间，且每10 mm进行一次测试，测试距离ρ为对应当时d的10组测量数据的平均值，具体数据见表1。

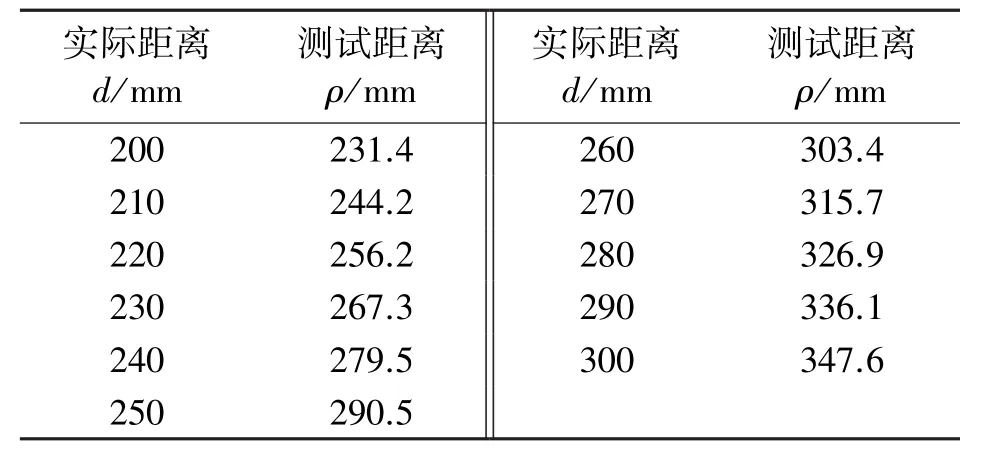
表1 初始拟合数据

根据上述测量数据，选用直线段进行最小二乘拟合，可以得出两者间的关系函数如下:

式中d′为根据拟合参数求得的距离值。

本测试数据中 α＝0.86，β＝0.33，，在实际应用测量时，为了能利用上述函数关系获得比较精确的测试结果，为此本文验证了测量精度。做法是随机选取20个精准距离值，再利用单目摄像头进行观察测量，获得测量值，分析这20组精准距离值与观察测量数据之间的误差大小，结果列于表2中。

表2 测试数据 单位:mm

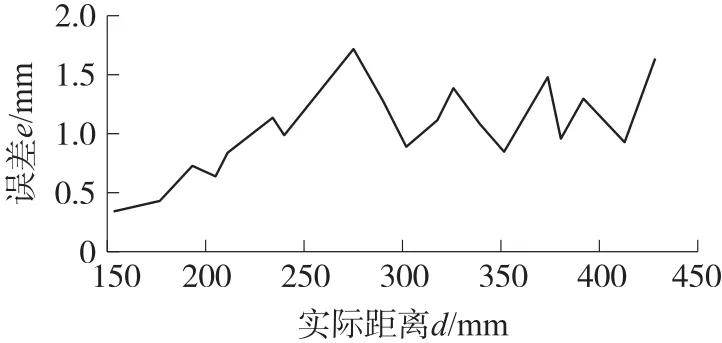
图11 测试精度

经测试随机选取20个距离值，测试距离误差均能稳定在2 mm以内。

3.2 摄像头位置变化实验

为了探究相机位置的变化是否会影响测量精度，本文做了两组实验，一组是将相机沿某一方向进行平移，观察测量误差的变化，另一组是改变相机拍摄角度，观察测量误差的变化。

实验1 相机水平移动对测量精度的影响

实验过程中固定两个标志点的距离为350 mm，对相机沿相机坐标系y轴方向进行平移，每次平移距离为5 mm共平移10次，每次平移测试10组数据取平均值作为实验数据。图12为实验误差变化图。

图12 平移对精度的影响

从图12中可以看出逐渐平移相机的位置，误差仍然保持在2 mm以内，且变化趋势无明显规律，仿真曲线抖动为正常系统误差。

实验2 相机拍摄角度的变化对测量精度的影响

实验中固定两标志点之间距离为350 mm，分别改变摄像头相机坐标系x轴以及相机坐标系y轴的角度，x轴角度区间为[-5，＋5](单位度)，y轴角度区间为[-1，＋1](单位度，实验中y改变角度过大会导致实验装置不稳定，因此区间为[-1，＋1])。逐渐改变相机的拍摄角度，图13、图14分别为x轴以及y轴角度改变对实验精度的影响示意图。

图13 x轴角度变化对精度的影响

图14 y轴角度变化对精度的影响

由图13和图14可以看出，角度的变化不会对实验精度造成影响。

4 结束语

本文提出了一种基于视觉和深度信息的山体裂缝宽度测量方法，通过识别放置于裂缝两侧的圆形标志点，并根据圆心的像素坐标搭配深度信息解算出两点在世界坐标中的距离，通过两个标志点的距离来反映裂缝的变化。实验验证了方法的有效性，精度在2 mm以内，高于常用的GPS方法的亚厘米级精度。同时摄像头的平移以及角度的变化对实验精度影响不大，测试精度在2 mm以内。证明本方法具有实用性，之后将会继续加强图像识别的稳定性以及探讨其他因素对测量精度的影响。