增强灰狼自适应阈值去噪法在变压器套管引线超声检测中的应用∗

王 硕，王 昕，蒋国臻，童 俊，钱 涛

(1.上海电力大学电气工程学院，上海200090；2.上海交通大学电工与电子技术中心，上海200240；3.国网浙江省电力公司建德供电公司，建德311600)

绝缘套管作为变压器的重要组成部分，不仅起到固定与保护引线的作用，还能在引线与油箱间起绝缘作用[1-2]。然而，变压器套管在运行中需长期承受电、热、机械力等因素的影响，绝缘性能与强度下降会使得套管端部的引线因承受电动力、机械力作用产生形变，对变压器的稳定运行造成巨大威胁[3-4]。因此，需采用有效的方法实现变压器套管引线的在线检测。

目前，针对变压器套管引线检测的方法极少，考虑到超声检测技术具有较强的穿透性和无损性[5]，安全简单，探伤灵敏度高[6]，在固体的形变与裂纹检测中得到广泛应用[7-8]。因此，使用超声检测技术可实现变压器套管引线的在线检测。

在超声检测过程中，回波信号在采集时极易受到环境噪声、电路耦合噪声等因素的干扰，使得信号信噪比降低，影响超声检测精度[9-10]。小波分析法因具有较强的时频分析能力，在超声波等非平稳信号去噪领域使用广泛。文献[11]对传统小波阈值函数进行改进，一定程度上提高了信号去噪效果，但小波基与信号分解层次的选择随机性较大，去噪时难以有效区分信号与噪声，损失有效信息；针对小波分解存在的上述问题，文献[12]提出了一种自适应小波去噪法，可适应性的估计不同尺度的阈值大小，但该方法的去噪时间过长，去噪结果不稳定，去噪的同时会导致原始信号产生畸变；文献[13]和文献[14]分别提出蚁群优化小波阈值法和混合粒子群自适应阈值去噪法用于非平稳信号去噪，试验结果表明，这两种方法虽都能减小去噪信号的畸变程度，但这两种方法在处理低幅值噪声信号时效果较差，如果阈值选取不当，去噪效果不彻底，容易造成信号有效信息的辨识度下降。

针对上述算法的不足，本文提出了一种增强灰狼优化自适应阈值去噪方法IGWOTE(Improved Gray Wolf Optimization adaptive wavelet Threshold Estimation)。首先，对信号进行多尺度小波分解，采用包含多阶连续导数的梯度下降自适应阈值法，可进行自适应迭代，适应不同种类的噪声信号。然后针对信号中的小幅值噪声，对自适应阈值函数进行寻优。通过改进原始灰狼算法 GWO(Grey Wolf Optimization Algorithm)的收敛算子与变异策略，优化自适应阈值函数的梯度值，使阈值函数能有效区分噪声与有效信息。再使用该最优阈值函数进行去噪处理，增强了有效信息的辨识度，提高了信号的信噪比与均方误差。最后对仿真超声回波信号及实测超声回波信号的去噪结果分析表明:本算法在去噪的同时保留了超声回波信号起振位置等有效信息，在变压器套管引线超声检测中，提升了超声检测精度，获取了变压器套管引线状态，具有一定的实用性。

1 变压器套管引线超声检测原理

1.1 超声检测原理

当超声波在不同介质中传播时，由于不同媒介间的声阻抗相异，在两种介质间的界面会产生反射回波信号，通过回波信号飞行时间的长短可计算出变压器套管表面与引线之间的距离，实现变压器套管引线的超声检测[15]。

为准确测量超声波的飞行时间，使用自相关算法，该方法根据信号的自身相关性，自动识别回波信号的起振位置。对于超声回波信号x(t)，在t与t＋Δt时间段内自相关函数Rx(Δt)如式(1)所示[16]。

对周期信号x(t)，其自相关函数Rx(Δt)也为周期函数，当时间间隔T为信号周期的整数倍时，自相关值为最大值，超声回波信号任意两个周期间的自相关值接近于1。因此，本文取回波信号峰值附近的多个周期信号，依次与发出的超声信号进行对比。通过两信号之间的相关系数即可判断出回波信号的有效周期，从而获取超声回波信号的起振位置，计算超声回波信号的飞行时间。

1.2 超声检测系统

本系统采用收发一体超声探头，中心频率为1 MHz。首先，信号发射电路激发超声探头产生高幅值脉冲信号，一段时间后，超声探头接收回波信号，信号经调理电路处理后传输至数据采集卡转换成数字信号，以便于信号二次处理，系统原理如图1所示。

图1 超声检测系统

已知变压器套管壁是由陶瓷构成，瓷套管内充满变压器绝缘油，套管正中心穿过导电铜杆，铜杆外包绝缘纸。在进行超声检测时，将超声探头置于变压器套管端部外壁A、B、C、D四个位置，探头与套管壁垂直并在两者之间涂抹超声耦合剂。首先，超声探头发出的超声信号经耦合剂垂直打入套管壁进入绝缘油中传播，当信号遇引线时会产生回波信号，然后该信号可通过超声探头转换成电磁脉冲信号，完成信号的采集。

理想情况下，20℃时超声波在变压器油中的传输速率V1为1.42 mm/μs，超声波在陶瓷中的传输速率V2＝5.84 mm/μs约为 V1的4倍。 此外，套管壁厚度ΔL约占引线距套管表面的距离L的1/5。由计算得，声波在套管壁中传输的时间约占总飞行时间t的5.7%，声波在变压器油中的传输时间约占总飞行时间t的94.3%。由上述分析可计算出引线与变压器套管之间的近似距离L，如式(2)所示。

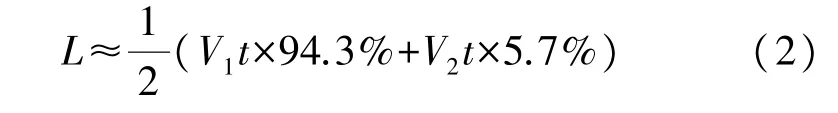
在进行结果判断时，需对比四组检测值。若四组检测结果近似于标准值，且彼此间数值差别不大，可认为变压器套管引线良好；若四组检测结果不相近且与标准值存在较大偏差，则变压器套管引线可能出现故障，需进一步检测，原理如图2所示。

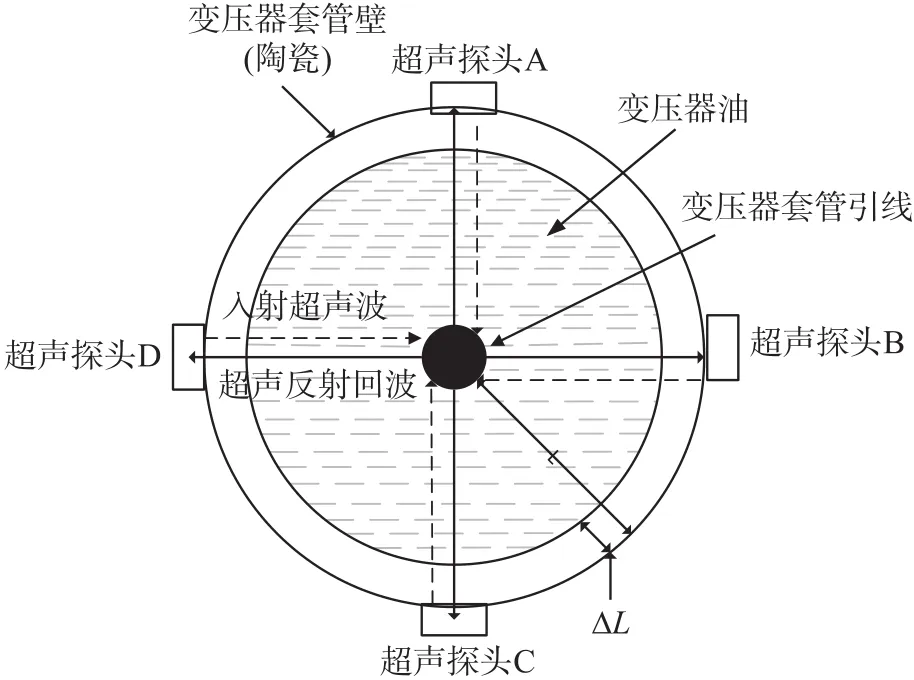
图2 基本原理示意图

2 增强灰狼自适应最优阈值算法

2.1 自适应最优阈值算法

假设染噪超声回波信号的观测值X＝[x0，x1，…，xi，…，xN-1]T，真实信号可表示为 e＝[e0，e1，…，ei，…，eN-1]T，则实测超声回波信号如式(3)所示。

式中:ni为独立分布的高斯白噪声。去噪的目的是获取含噪超声回波信号X的估计信号，使得¯e与e的均方误差尽可能小。

自适应小波阈值估计采用梯度下降法，下一刻阈值λ(t＋1)等于此时阈值减去均方误差函数梯度值Δλ(t)，如式(4)所示。

式中:dj，k为 j尺度上的小波系数，∂η(dj，k，λ)为阈值函数，gi为函数估计表达式，如式(6)所示。

为了有利于阈值函数的自适应迭代，本文使用Sigmoid函数作为阈值函数[17]，如式(7)所示。

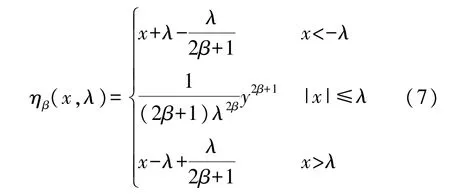
式中:β为正整数，取值为2。求其一阶导数与二阶导数并代入(4)、(5)即可进行自适应迭代得最优小波阈值。

2.2 增强灰狼算法

GWO算法是一种模拟狼群捕猎行为的仿生优化算法，模拟狼群寻找最短捕猎路径[18]。该方法将狼群个体分为首领狼α、副首领狼γ、普通狼σ以及底层狼ω。其中α狼权力最大，数量最少，调整狼群的捕猎方向；γ狼和σ狼的权利依次减少，辅佐α狼；狼权力最小，数量最多，为 α、γ、σ 狼提供信息[19]。

狼群在开始捕猎之前，需要先根据式(8)、式(9)包围猎物:

式中:t为迭代次数，Yp(t)为猎物位置，Y(t)为狼群个体位置；C＝2r1代表摆动因子；A＝2ar2-a代表收敛因子；r1，r2为取值为[0，1]的随机数；a的值呈线性变化，随迭代次数的增加从2衰减至0。

狼群成功包围猎物之后，将由α、γ、σ狼判断猎物方位，决定狼群位置Yp(t＋1):

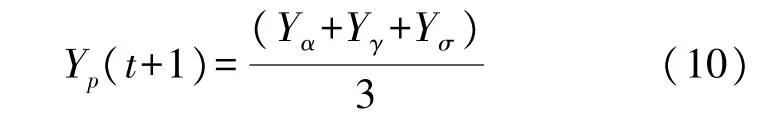
式中:Yα、Yγ、Yσ分别代表 α、γ、σ 狼个体位置，由式(8)、式(9)可得。

由传统GWO算法可知，收敛因子A与变异策略控制着算法的寻优过程，但此过程极易陷入局部最优解，造成去噪后信号细节信息丢失、去噪效果不彻底甚至信号大幅度畸变，不利于判断信号起振位置，影响超声检测精度。因此，对原始GWO算法的动态数值a及变异策略Y进行改进得到增强灰狼算法(IGWO)，如式(11)、(12)所示。

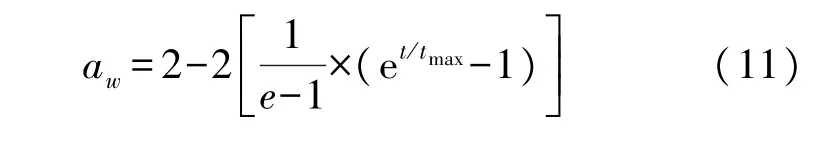
式中:tmax为最大迭代次数，t为当前迭代次数。

式中:rand为[0，1]间的随机数，b1为个体学习因子，b2为群体学习因子，(t)为第t次迭代为止w狼位置为最佳狼群位置。

2.3 算法实现

增强灰狼自适应阈值去噪法的步骤如下:①设定IGWO算法中狼群数量S，最大迭代次数Tmax，优化参数个数dim，个体学习因子b1，群体学习因子b2。②狼群初始化，满足约束条件并确定狼群初始位置向量，确定a、A、C，生成初始狼群。③根据式(5)计算狼群中每只狼的Δλ，当Δλ为最小值时即为最优λ值。以此为依据选择三个最佳个体作为α、γ、σ狼的位置。④α、γ、σ狼指导狼群进行捕猎，依据式(12)更新狼群的位置坐标，保留适应度最佳个体位置并进行迭代，实现狼群位置更新。⑤判断是否满足终止条件，若满足则输出最佳阈值λm终止迭代，否则转入②，继续迭代。

超声波信号近似正弦分布，使用sym6小波基小波分解。本文IGWO算法参数设定如下:狼群数量S＝30，最大迭代次数Tmax＝100，优化参数个数dim＝1，个体学习因子 b1＝1，群体学习因子 b2＝1。

算法流程图如图3所示。

图3 系统流程图

3 仿真分析与实例验证

3.1 仿真分析

超声波是一种非平稳时变信号，遇到障碍时会产生底面回波、缺陷回波与材料散射回波等[19]。在窄脉冲超声检测中，依据超声波信号的物理特性，其回波信号可模拟成高斯信号，如式(13)所示[20]。

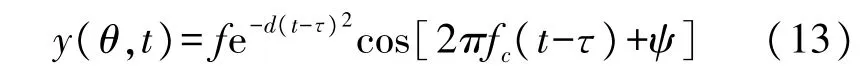
参数设置如表1所示，超声发射信号与回波信号分别如图4(a)、4(b)所示。对信号添加能量大小为0.005 dBW随机噪声，模拟染噪超声信号，如图5。

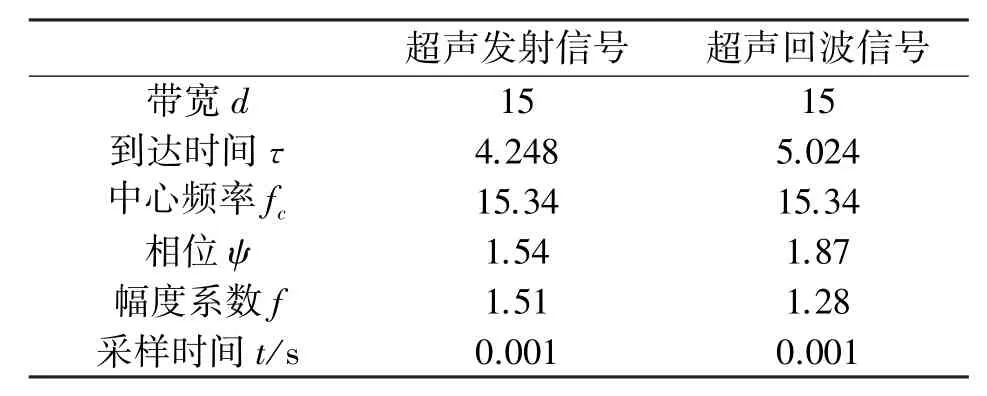
表1 参数解析

图4 仿真超声回波信号

图5 染噪仿真超声回波信号

为了更好的检测本文增强算法的去噪效果，引入基于梯度下降的自适应阈值法(Adaptive wavelet Threshold Estimation，ATE)、粒子群优化自适应阈值法(ParticleSwarm Optimization adaptive wavelet Threshold Estimation，PSOTE)、灰狼优化自适应阈值法(Gray Wolf Optimization adaptive wavelet Threshold Estimation，GWOTE)与本文算法进行比较，去噪后的信号如图6所示。

图6 去噪后信号

由图6可得，经ATE法去噪后信号虽含较少噪声，但其波峰产生了一定程度的畸变，起振位置被破坏，在去噪的同时改变了波形完整性，波形中仍含较多噪声，不利于提取有效信息；经PSOTE、GWOTE法去噪后，虽信号波峰畸变程度得到较好的改善，但去噪效果仍不彻底，波峰前后仍含较明显噪声，不利于有效识别波形起振位置；而经IGWOTE去噪处理后的信号整体效果更好，波峰突变程度最小，含有更少的毛刺噪声信号，信号突变量更小，更有利于识别信号起振位置等更多的细节信息。

为了进一步体现本文算法的去噪效果，引入信噪比(SNR)、均方误差(STD)、算法运行时间(T1)与信号飞行时间(T2)作为评价标准。其中信噪比越大，均方误差越小说明去噪效果越好；运行时间越短，去噪效率越高。信号飞行时间由表1可得约为0.776 s。去噪后信号的各项指标如表2所示。

表2 信号去噪标价指标

由表 2数据可得，IGWOTE法相较于 ATE、PSOTE、GWOTE三种算法，去噪后信号的信噪比更大，均方误差更小，算法的运行时间更短，更高效，相对于与原信号的畸变率最小。从超声检测结果上来看，IGWOTE法去噪后信号的飞行时间0.79 s更接近于标准结果0.776 s，表明本算法在去噪的同时，波峰畸变程度最小，更好地保留了信号中起振位置等细节信息，有利于测量信号飞行时间，提高超声检测系统的精度。

3.2 实例验证

为了验证本文去噪法在超声检测中的效果，在浙江省建德市110 kV变电站进行变压器套管引线超声检测。选用一台110/35 kV的变压器为实验对象，选择B相套管进行超声检测，引线与套管外表面距离约为66 mm，现场检测如图7所示。

图7 现场检测图

为了便于信号的观测与处理，将超声发射信号与回波信号分离，超声发射信号与回波信号分别如图8、图9所示。

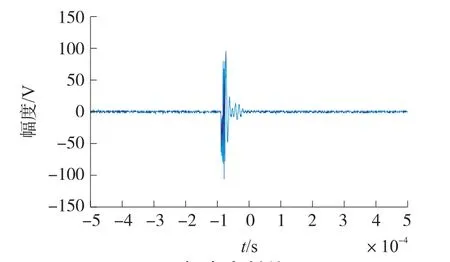
图8 超声发射信号

由图9可看出，超声回波信号中含有较多的噪声干扰，因此需进行去噪处理，分别采用 ATE、PSOTE、GWOTE、IGWOTE四种方法去噪。为了简化分析，本文仅对CHA回波信号去噪处理，去噪后的超声回波信号如图10所示。

由图10可得，回波信号在经ATE法去噪后虽能过滤大部分噪声，但在去噪的同时破坏了信号的完整性，波峰及波尾部分产生严重畸变，波峰前后起伏较大，波形平滑性较差；经PSOTE法去噪后，虽能极大限度地保留信号的完整性，波峰畸变程度减小，但波尾部分仍存在波形畸变情况，波形中存在噪声，去噪效果不彻底；而经GWOTE、IGWOTE去噪后，在去噪的同时极大限度地降低了信号的畸变程度，无论从波形完整性还是波形平滑性上来看均优于其他算法，去噪后信号含有较少的毛刺信号，相较于GWOTE法，IGWOTE法去噪后信号波峰波尾畸变程度更小，去噪效果更好，更有利于识别回波信号起振位置。为了进一步体现去噪效果，需对去噪信号进行信号信噪比与均方误差计算，四组计算结果如图11所示。

图9 超声回波信号

图10 超声回波信号去噪效果图

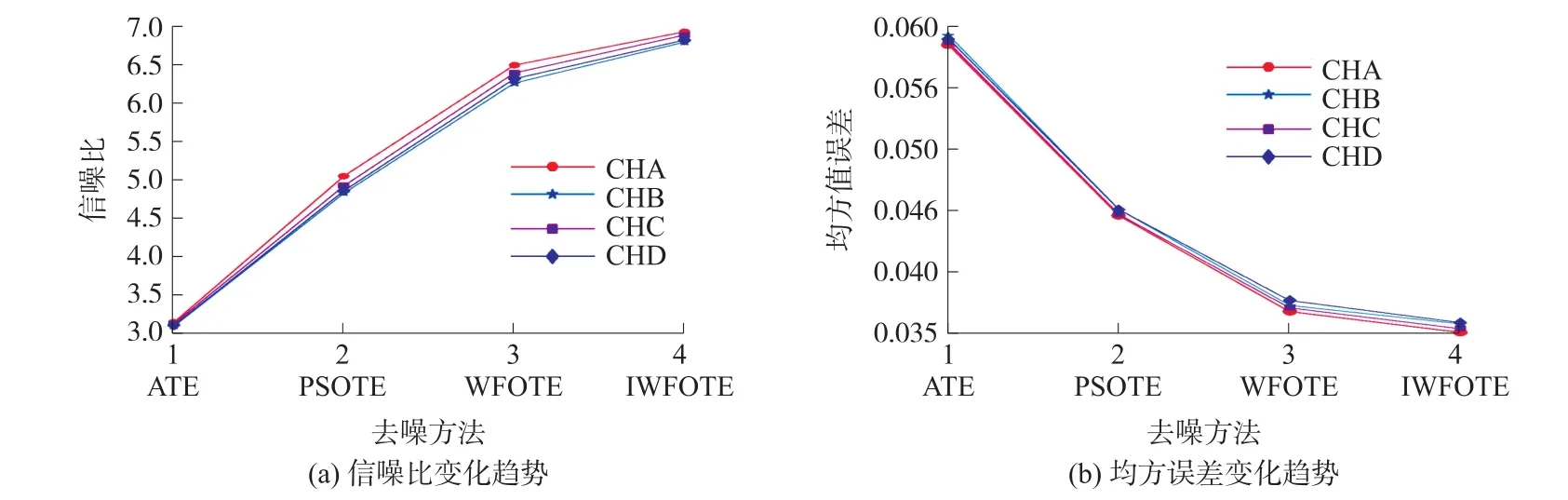
图11 信号信噪比与均值误差

图11(a)、11(b)分别为去噪后四组超声回波信号的信噪比与均值误差在不同算法下的变化趋势，四组超声回波信号经IGWOTE去噪后信号信噪比均高于ATE、PSOTE、GWOTE算法，均值误差均小于ATE、PSOTE、GWOTE三种算法，去噪后的回波信号质量最佳。为验证算法去噪效率，测量算法运行时间，结果如图12所示。

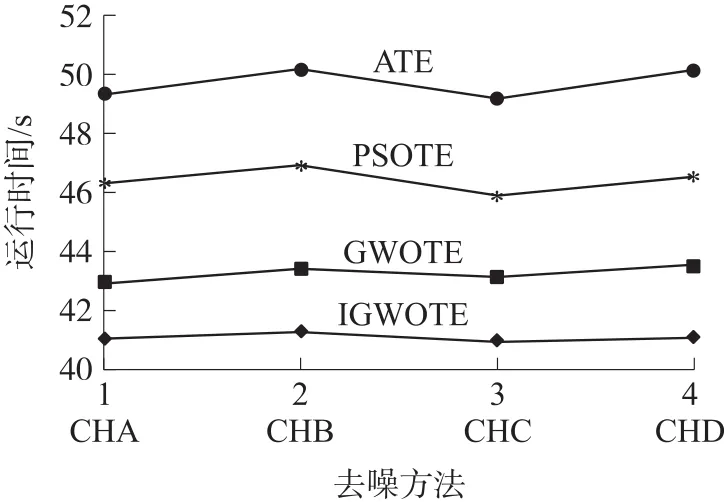
图12 各算法运行时间变化趋势

由图12可知，本文IGWOTE去噪法的运行时间均小于其他三种算法，效率最高。最后，将上述四种去噪后信号引入超声检测系统，结果如表3。

表3 超声检测结果 单位:mm

从表3数据来看，四组测距结果均小于实际测量值，是超声信号传输速率衰减造成的影响，符合实际情况。此外，经IGWOTE去噪后的四组信号在超声检测中所得结果更接近于测量值66 mm，这说明，本算法在去噪的同时更好地保留了回波信号起振位置、信号波峰等细节信息，极大限度地保留了信号的完整性，降低了去噪过程导致的信号畸变率，相较于其他三种方法去噪效果最好，能更加准确地测量超声回波信号的飞行时间，更为精准的求出引线至套管壁之间的距离，实现变压器套管引线的超声检测。此外，四组超声检测结果类似，数值无较大的变动，表明变压器套管引线状态良好，较为真实地反应变压器套管引线的状态。

综上所述，本文提出的IWGOTE去噪法，既能去除超声回波信号中的随机噪声干扰，提高信号质量，节省运行时间，还有助于提高超声检测的测量精度，提高了变压器套管引线超声检测的准确性。

4 结论

本文基于一种包含多阶连续导数的梯度下降自适应阈值法，结合增强灰狼优化算法，实现了超声回波信号的去噪功能。对仿真超声回波信号及实测超声回波信号的去噪实验分析，得到如下结论:

①通过包含多阶连续导数的梯度下降自适应阈值函数实现了小波系数自适应阈值的选取。结合提出的增强灰狼优化算法，解决了传统迭代阈值去噪法阈值不准确，寻优慢的缺点，可高效寻找最优阈值。

②对仿真及实测超声回波信号进行去噪，对比分析了 ATE、PSOTE、GWOTE、IGWOTE 四种方法的去噪效果，实验结果表明，IGWOTE法比其他三种算法的去噪效果更好，信噪比更高、均方误差更小，超声回波信号起振位置等有效信息得以保留，进一步减小了信号的畸变程度。

③将本文IGWOTE去噪法应用到变压器套管引线超声检测中，与其他三种算法相比。经IGWOTE法去噪后，信号质量最高，提高了超声检测精度，有利于获取变压器套管引线状态，具有一定的实用价值。