基于超声相控技术的新型船舶计重方法研究∗

叶晓同，赵 鹏∗，李存军，郝华东，施浩磊

(1.中国计量大学计量测试工程学院，杭州310018；2.舟山市质量技术监督检测研究院，舟山316013)

随着我国对外贸易的不断发展，关系到国计民生的大宗海运散货进口量逐年快速增长，对船舶计重的要求越来越高。目前常用的船舶计重方法为水尺观测法[1]，水尺观测法是建立在读取待测船舶吃水刻线的基础上，通过船舶六面水尺的测定，依据船舶的准确图表来计算载运货物重量，包括人工观测法、压力传感法、图像检测法、激光测量法、超声检测法等[2-5]。由于超声波在水下穿透能力强、对人体无害等优点，使得侧扫声纳[6]、多波束声纳[7]、合成孔径声呐[8]和前视声呐[9]等在船舶计重方面的应用越来越广。

刘新[10]等提出了一种基于超声波液位测量技术的内河船舶载重测量方法，大幅度提高相对传统目测方法得出的船舶载重精度值，但测量条件受限，精度有限；吴俊[11]等利用单波束声呐进行船舶吃水测量，得到吃水误差为3.3%，误差较大且测量范围较小。之后王培滨[12]等提出了一种侧扫式船舶吃水检测系统，该方法虽然提高了测量范围，但需要安装多个换能器阵列，安装检修不易。为了进一步提高测量精度，陈德山[13]等提出了一种基于多波束仰扫的内河船舶吃水检测技术，该方法测得的吃水深度与真实吃水值比较接近，但多波束声呐目前多依靠进口，成本较高。并且上述方法也无法从根本上消除船体变形引起的形变误差或者纵倾、横倾引起的倾斜误差。

超声相控技术作为一种超声检测手段，无需通过机械移动探头即可实现空间区域的大范围扫描[14]，且可有效地调节声波信号的辐射和声波聚焦位置等聚焦参数，能够获得较高的空间成像分辨率和检测精度[15]。并且超声阵列换能器制作简单，成本较低，在各种检测领域应用已相对成熟。本文以超声相控阵技术为基础，将超声阵列换能器应用于船舶计重，通过对水下船体进行相控扫描，获取水下船体三维模型并计算体积，根据阿基米德定律计算出载重从而减小传统水尺在读数时引起的误差。

1 基本原理

1.1 超声阵列换能器的声场辐射

利用惠更斯原理[16]，将超声阵列换能器中每个阵元看作独立声源，分别求出每个阵元对声场的贡献，再叠加起来，就可以得到整个阵列声场空间中任意位置的声压值。一维线性超声阵列换能器的空间位置分布如图1所示，将X轴方向定为换能器长度方向，Y轴方向定为换能器宽度方向。单个换能器阵元可划分为无限多个尺寸极小(远小于声波波长)的微面元ds，此时微面元可作点声源处理，其辐射声压表达式为:

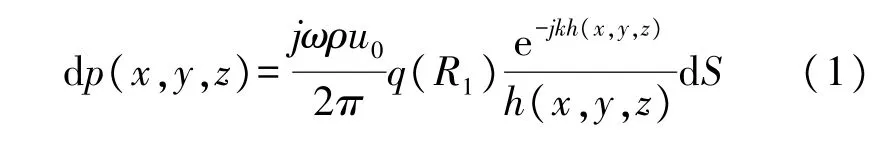
式中:ω为角频率，k为声波波数，c为声波在介质中的传播速度，ρ为介质密度，u0为换能器辐射面中心处的振速，q(R1)为归一化振速分布系数，R1为换能器辐射面的半径变量，h(x，y，z)为该面元与观察点之间距离。

对式(1)进行面积分，则声场中某一点的Q的声压可表示为:

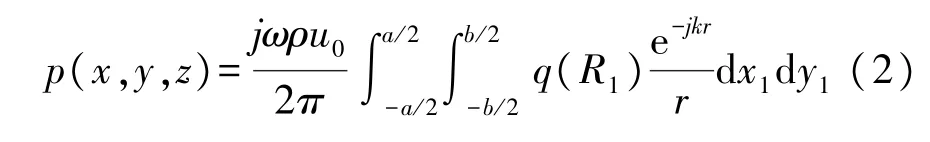
式中:r为Q点与面元的距离。

图1 超声阵列换能器空间分布

假设辐射面的振速均匀分布，即q(R1)＝1。因此，阵列在Q点的声压等价为单个阵元在该点的声压的叠加:

式中:m＝1，2，3，…，M，n＝1，2，3，…，N，即将单个阵元划分为M×N 个微元；i＝1，2，3，…，K 为阵元序列；rm，n，i为辐射平面内第M×N个微元与声场中任意观察点之间的距离。

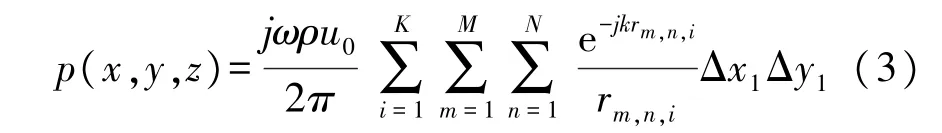
1.2 超声相控阵原理

将超声相控阵列视为相干声源，控制各阵元晶片的发射时延，可形成具有聚焦或偏转特性的声场[17]。通过改变相位延迟，实现聚焦位置的更变，完成查扫功能。图2所示为焦点偏转至P点时的几何示意图。

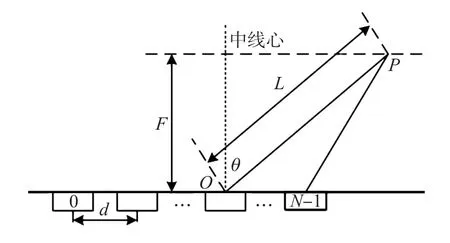
图2 相控声束偏转

以阵列中心作为参考点，第n个阵元到焦点P的距离为:

式中:k＝n-(N-1)/2。

则可以得出中心阵元与阵元n之间的时延差为:

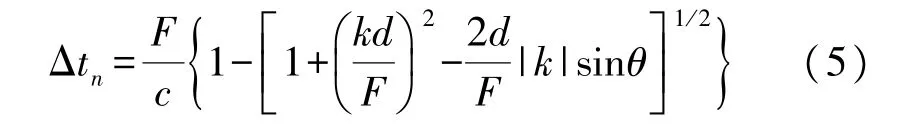
式中:n＝1，2，…，N-1，F 为焦距，d 为相邻阵元中心间距，θ为声束偏转角，c为声速。

1.3 计重原理

船舶计重方法基于阿基米德原理，通过装载货物前后排水量之差计算船舶装载货物的重量，实现计重。实际测量中首先利用超声阵列换能器扫描获取水下船体三维模型，然后计算出三维模型的体积也就相当于得到船的排水量，最后通过装载货物前后排水量差计算重量。

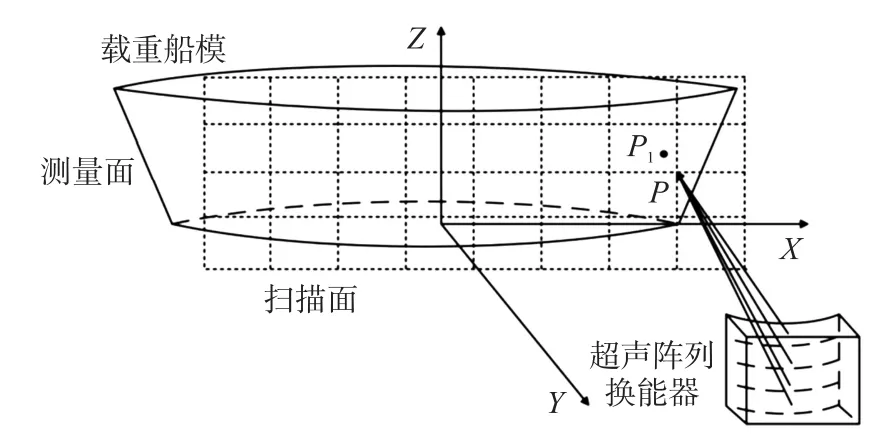
图3 扫描示意图

超声阵列换能器扫描示意图如图3所示，由于载重船模中心对称，因此将模型简化为半侧扫描然后镜像处理。设置载重船模Y轴正方向的侧面为测量面，首先在测量面附近定义一个扫描面，将扫描面离散为若干扫描点，依次对这些扫描点进行扫描，在扫描时根据式(5)计算每个阵元的发射时延，使声束聚焦在扫描面上的P点。此时有效聚焦范围内位于船侧的P1点散射回来的声回波信号被换能器接收阵元接收，回波信号如图4所示，整段脉冲回波信号分为暂态和稳态。通过峰值检测，得到其回波的包络，可看做脉冲阶跃响应，依据系统动态性能指标，本文将小于稳态的10%所对应的第一个暂态峰值作为回波的接收时间。根据回波时延可计算出P1点与各接收振元距离，利用双曲线交汇法计算出交点即P1点坐标。由于一维线阵只能实现换能器长度方向相控(图中Z轴方向)，因此利用相控改变扫描面上P点位置只能获得测量面上Z轴方向一个剖面轮廓上的点，要获取其他剖面轮廓上的点需要在X轴方向移动超声阵列换能器。

图4 回波信号

假定扫描获取水下船体模型如图5所示，沿着X轴，以间距Δx将船体划分M个横剖面，则相邻两个横剖面所包围的空间的体积Vi可表示为:

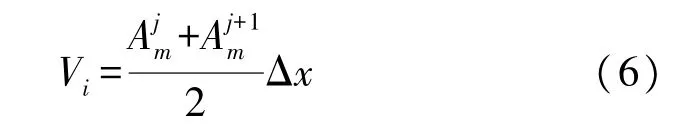
式中:j＝1，2，3，…，M-1。

图5 水下船体模型

利用梯形面积公式，任意横剖面的面积为:

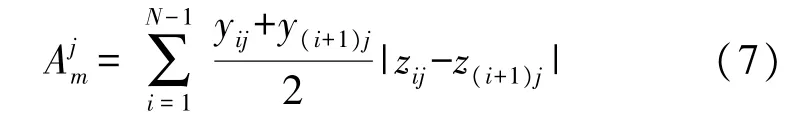
式中:i＝1，2，3，…，N-1，yij、zij为第 j条横剖面扫描线上第i个点的Y轴坐标与Z轴坐标。

则整个船体的体积可由式(6)计算得到:

根据式(8)，可计算船舶的排水体积，则船舶净载量可表示为:

式中:ρ、V0和V分别表示水密度、船舶空载排水体积和装载后的排水体积。

2 实验测试

2.1 换能器实验测试

线性超声阵列换能器的阵列参数对聚焦性能有直接影响[18]，为确保阵列换能器具有良好的聚焦性与声指向性以及将旁瓣干扰降至最小，依据文献[18]结论，设计的换能器阵列由32片压电陶瓷片构成，每片阵元可单独发射声波信号，并且阵元4、阵元12、阵元20和阵元28还可用作回波接收。每片阵元的阵元宽度为3.6 mm，长度为120 mm，相邻阵元中心间距为4 mm，阵列的工作频率为500 kHz。为了提高换能器的聚焦性能，在换能器阵列前端加装焦距为800 mm的声透镜，实现换能器宽度方向自聚焦，换能器实物如图6所示，换能器长160 mm、宽152 mm。

图6 换能器实物图

利用MATLAB对换能器声场进行仿真，在仿真时，设置换能器阵列各项参数与所用换能器一致，相控聚焦在距换能器表面800 mm的地方，然后分别使焦点偏转不同的方向，计算出各偏转位置换能器长度方向与宽度方向的主瓣高度与主瓣宽度，结果如表1所示。

同时利用水听器扫描法对相同条件下的声场进行扫描，其结果如表2所示。

由表1与表2可知，换能器实测结果与仿真结果基本一致，阵列换能器在相控偏转-60 mm到60 mm能够在800 mm处形成聚焦声场，且声压没有明显降低，该阵列换能器具有良好声指向性且可旁瓣干扰较小，可以进行相控聚焦偏转扫描。

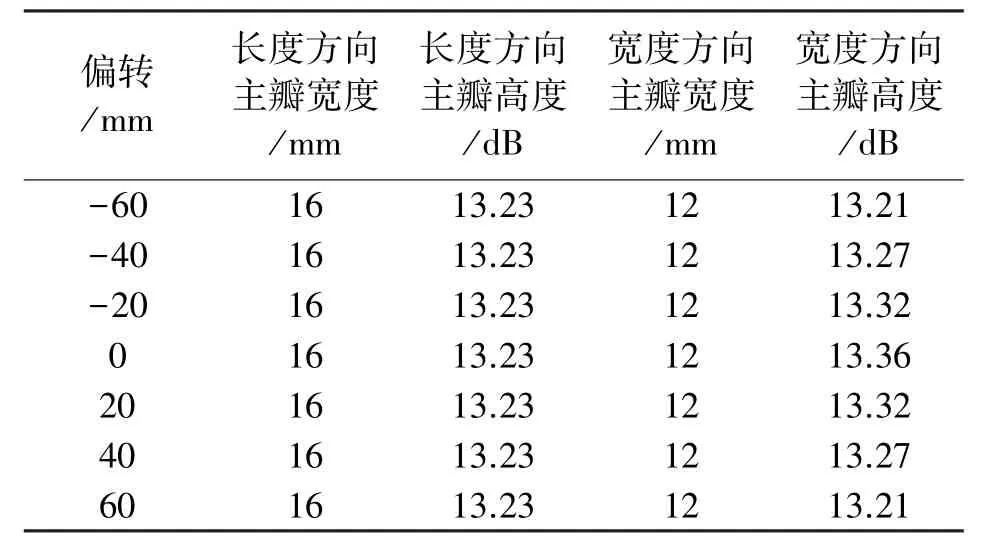
表1 各偏转方向仿真声场数据

表2 各偏转方向实测声场数据

依据图3扫描方法，需要确定船体的有效聚焦范围，以声压最大值降低-6 dB的范围作为有效聚焦区域，对换能器声轴方向声压进行仿真与测试，结果证明换能器有效聚焦区域为距换能器表面600 mm至1 250 mm的地方。在此区域内换能器聚焦效果较好，经被测物体散射后回波信噪比最好。

2.2 计重实验测试

为验证方法可行性，搭建了如图7所示实验系统，系统主要由超声阵列换能器、计重船模、模拟负载装置、牵引装置、超声相控阵收发系统和上位机组成。上位机控制超声相控阵收发系统发出填充脉冲信号激励换能器，信号经声透镜与相控聚焦后汇聚在船侧附近，在经过船模反射后被换能器的接收振元接收，然后被超声相控阵收发系统采集传送至PC机处理。超声阵列换能器通过硬连接固定在牵引装置上，牵引装置在运动时会带动换能器同时运动，计重船模放置在距换能器有效聚焦范围内，图中为800 mm，用模拟负载装置对计重船模施加载重。

设备搭建完成后，控制超声阵列换能器按照图3所示方法进行相控扫描。当一条剖面线扫描完成后利用牵引装置将换能器运动一段距离，再一次对水下船体进行扫描，得到下一条船体半剖曲线，直至对水下船体完成扫描。设置每条扫描线40个扫描点，相邻扫描点间距为3 mm，单条扫描线长为120 mm；牵引装置控制超声阵列换能器单次移动步进为5 mm，移动次数200步。即在120 mm×1 000 mm的扫描范围内扫描8000个点。扫描得到的回波信号如图8所示，在测量时，由于船模本身有一个厚度，信号经过这个厚度后再反射回探头，会和回波信号叠加在一起形成一种有规律性的干扰信号，为了消除干扰信号对测试结果的影响，计算时首先对回波信号进行匹配滤波，提高信号的信噪比，之后通过峰值检测，得到回波的包络，然后根据图4所述方法获取回波信号的接收时间，由于时延计算是利用回波信号的第一个周期，而干扰信号要迟于回波信号几个周期到达，因此可忽略干扰信号对时延计算的影响。

图7 测量系统示意图

图8 接收回波信号

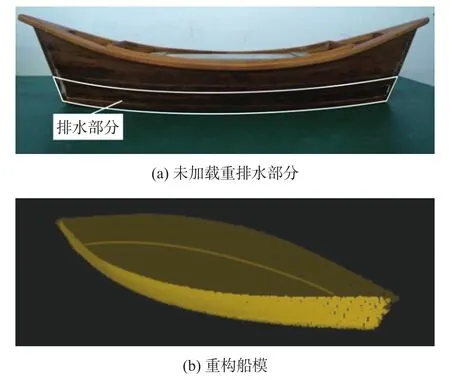
图9 测量结果

图9(a)所示为所用船舶模型，其中排水部分即为未加载重时的扫描面，随着载重增加排水部分的高度将增加，扫描获得的三维模型如图9(b)所示。

利用模拟负载装置对船模施加不同的载重，获得不同排水时的水下船体三维模型，然后利用式(6)～式(8)计算得到不同载重时的吃水深度与计重结果，如表3所示。

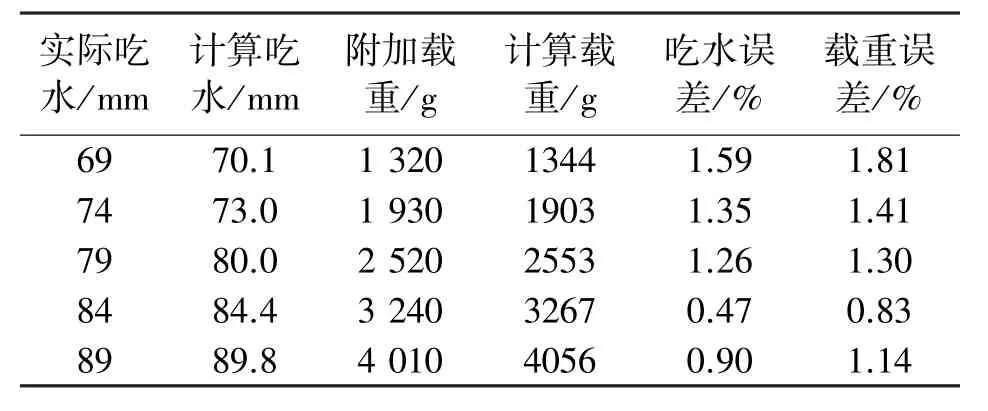
表3 测量结果表

由表3可知，相比于文献[11]中的单波束侧扫声呐法，同样在静水环境下对船模进行测试吃水误差在3.3%，本文采用的基于超声相控阵的测量在吃水深度的测量上极大减小了误差，将吃水误差控制在2%以内。计重误差最大为下降10 mm的时候，此时误差1.81%；最小为下降25 mm时，误差为0.83%，在测试的几组吃水深度计重误差都在50 g以内。分析误差产生原因，主要有各散射点位置计算不准引起的误差与船体不完全对称引起的镜像误差。

根据系统的计重模型，对误差源进行分析，计重误差可分解为船舶加载前后排水体积误差和密度误差。由于密度误差主要与密度计和水采样深度有关。因此，仅对船舶排水体积误差进行讨论，由式(6)、式(8)可得体积V为:

式中:Δx为相邻两扫描剖面之间的距离，在实验中，Δx为固定值，由牵引装置控制，根据式(7)可知体积V与扫描获取的散射点坐标有关，对单扫描剖面的面积进行误差分析:

在实验中，依据前文所述扫描点位置计算方法可将空间距离误差控制在一个波长以内，因此当频率固定不变时，由时延计算引起的坐标误差Δyij、Δzij最大值保持不变。则式(11)可简化为:

式中:a、b为常量。随着船体积的增大，各扫描点坐标的y值将越来越大，因此的值会减小，单个剖面的相对误差随之减小。同理，由式(10)体积计算公式计算出的排水体积的相对误差也会减小。

3 不确定度分析

计重误差的数学模型为:

式中:Δm为计重误差，P为测量重量，m为压力传感器读数。

①输入量m的标准不确定度评定，输入量m采用B类方法评定，查阅所用模拟载重装置技术手册，10 kg以内的误差为±20 g，取均匀分布，则标准不确定度u(m)＝11.55 g，自由度v(m)＝∞。

②输入量P测量重复性的标准不确定度评定，在测量船模下降20mm时，进行重复测量，测量结果如表4所示。

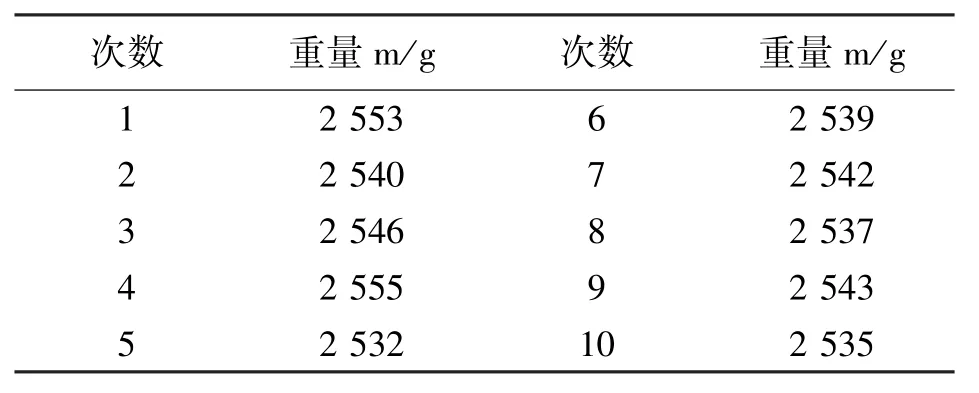
表4 重复计重测量结果

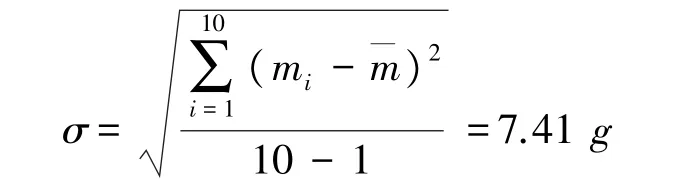
③输入量P分辨力引起的标准不确定度评定，测量结果的实际分度值d＝1 g，且服从均匀分布，则标准不确定度u(P)＝0.58 g，估计2则自由度v(P2)＝50。

因分辨力引入的不确定分量包含在重复性引入的不确定分量中，且远小于重复性的不确定度，可忽略其不确定分量，所以合成标准不确定度为u(P)＝.34 g，自由度 v(P)＝ 10。

输入量m与P彼此互不相关，所以合成标准不确定度uc(Δm)＝＝11.78 g，合成标准不确定度的有效自由度6 419，取 veff＝∞。

取置信概率p＝95%，按有效自由度veff＝∞，查t分布表得kp＝t95(∞)＝1.96，则扩展不确定度U95＝t95(∞)·uc(Δm)＝ 23.09 g，则在计重船模下降20 mm时测量结果的扩展不确定度为U95＝23.09 g，此时有效自由度 veff＝∞，相对扩展不确定度为0.908%。

4 结束语

本文提出了一种成本较低，安装简单、计重误差较小的船舶载重计量方法。分析了利用超声相控阵技术实现船舶载重的理论原理，并对所用超声阵列换能器做了声场测试，然后进行了船模载重测量实验，得到了水下船体重构模型，根据计重模型对误差源进行了分析，并推导了排水量对计重误差的影响，最后对计重结果的不确定度进行评估，结果表明，本文提出的基于超声相控阵技术的船舶载重计量方法能够实现载重计算，为船舶计重提供了一种可行的方法。

对于本文所用的一维超声阵列换能器，目前只能实现一个方向的相控扫描，还需要借助行走机构实现二维扫描，接下来可设计成二维线阵换能器，实现两个方向的相控扫描；并且在底部和两侧都放置换能器使适用范围更广，此外测试所用计重船模较小，与实际载货船舶相差较大，本文仅仅做了方法验证，接下来可以用大型载货船舶进行实验。