基于TDOA方法的无线传感器网络运动参数估计方法∗

徐城旭，吴晓平∗，王国英，朱雪芬

(1.浙江农林大学信息工程学院，浙江 临安311300；2.浙江农林大学信息与教育技术中心，浙江临安311300)

无线传感器网路由大量廉价、低功耗的节点组网而成，以实现对环境信息的监测，其具有有限的感知、计算与通信能力[1-2]。为弥补传统传感器网络上述缺陷，采用移动目标节点进行覆盖与感知增强[3]、目标跟踪[4]，即移动传感器网络亦是该领域重要的研究内容。移动目标感知的信息与位置相捆绑才有意义，因此传感器网络中移动目标的运动参数获取亦具有重要的研究价值[5-7]。

移动目标运动参数获取的重要内容就是估计移动目标的当前位置参数或预测将来的位置参数[8-9]。为获取当前位置参数即确定移动目标位置坐标，通常需要测量网络节点间距离，再利用算法估算移动目标的位置参数。常用的节点间距离测量方法包括到达时间(TOA)[10-11]、到达时间差(TDOA)[12]、到达角度(AOA)与信号接收强度(RSS)[13]等。TOA测量方法实现原理简单，但时间测量依赖于节点间的时间同步技术。并且节点上的计时时钟受到环境参数的影响会发生漂移和偏离，导致出现节点间的时间测量同向误差。而采用节点间TDOA时间差测量方法消除了同向误差，更易实现可靠的节点间距离信息提取。

以节点间的距离约束关系建立优化方程，再采用定位算法估计节点位置坐标。常用的定位算法包括极大似然(ML)估计法、最小二乘线性代数法[14]及凸优化算法[15-16]等。ML估计法一般采用数值计算方法估计，但数值计算方法严重依赖于初始解，若初始解选择不合适，有可能导致局部最优，为此提出了线性代数法及凸优化方法。线性代数法将计算结果直接表示为最小二乘代数解，计算过程较快。凸优化算法中常见的主要为半正定规划(SDP)算法，SDP算法将非凸优化模型松弛为凸优化模型，具有较多的变量和等式约束，计算复杂度较高，但算法稳定性较好。

在移动目标的运动参数获取过程中，将来的位置参数预测与滤波也是重要的研究内容。常用的移动目标位置预测与滤波方法包括航位推算[17]、即时定位与地图构建[18]以及滤波方法[19-20]等。航位推算通过轮子旋转数量来估算前进距离，以此确定位置坐标，但轮子有可能打滑而导致估算不可靠，并存在累积误差。采用移动目标的即时定位与地图构建方法通过开发环境地图以获取位置信息，地图构建的计算复杂度较高。滤波方法通过持续的预测与更新以提高移动目标的跟踪精度，包括适用于高斯噪声的卡尔曼滤波(KF)方法、扩展卡尔曼滤波(EKF)方法以及非高斯噪声的重采样粒子滤波(PF)方法等。

采用移动目标与信标节点间的TDOA测量方法，本文介绍了一种无线传感器网络中移动目标的运动参数估计方法。通过建立移动目标运动参数的优化估计模型，设计了基于TDOA方法的移动目标初始位置及运动速度的非约束线性最小二乘(ULLS)估计方法。并将约束条件运用到凸优化模型，实现了半正定规划(SDP)算法的设计。将TDOA测量方法的移动目标运动参数估计算法与文献[21]的TOA方法进行比较，分析TDOA方法对同向误差的消除有效性，同时分析了采样周期及采样点数量对估计精度的影响。

本文第1部分首先介绍了移动目标与信标节点间TDOA测量实现运动参数估计的问题描述；第2部分推导了问题模型的线性代数ULLS计算方法；第3部分提出了问题模型的SDP算法；第4部分为仿真分析；最后部分为结论。

1 问题描述

假设在二维平面(三维空间的分析方法同二维平面)有一移动目标节点从初始位置x0＝[x0y0]T出发，以恒定速度ν＝[νxνy]T保持匀速移动。为确定移动目标节点的位置坐标，在该区域上部署着M＋1个时间同步的信标节点，其坐标位置为已知值。将信标节点位置表示为 si＝[aibi]T，(i＝0，1，2，…，M)，信标节点保持不动，位置坐标固定。不失一般性，不妨假设i＝0信标节点为参考信标节点，并将i＝1，2，…，M的信标节点称为测量信标节点，如图1所示。

在移动目标节点移动过程中，各信标节点与移动目标节点间以等间隔周期T不断测量TDOA到达时间差。在第k个采样时刻，可将移动目标节点的位置坐标xk表示为

式中:k＝0，1，2，…，K，xk＝[xkyk]T表示了在第 k 个采样时刻的移动目标位置，T称为采样周期，K为采样点数量，即为目标移动过程中的TDOA测量次数。

在目标移动过程中，各信标节点与移动目标节点间的TDOA到达时间差测量过程如下:在第k个采样时刻，移动目标节点同时向各信标节点(包括参考信标节点)发送信号，各信标节点记录该信号接收时间。由于各信标节点间时间同步，故可以计算出信号到达测量信标节点与参考信标节点间的TDOA到达时间差。然后将所收集的TDOA测量结果统一发送到网关或集中处理单元，进行运动参数运算与估计。在第k个采样时刻，将上述TDOA到达时间差记为 ti，k，故有测量方程

式中:di，k＝‖xk-si‖，不失一般性，将参考信标节点的位置坐标假设为坐标原点，即s0＝[0 0]T，因此有 d0，k＝‖xk‖。 εi，k表示了移动目标节点与测量信标节点i间的时间测量噪声，可假设εi，k服从均值为零，方差为的高斯分布，记为 εi，k∈Ν(0，) 。

本模型通过移动目标与信标节点间的TDOA到达时间差测量，以准确估计移动目标的初始位置x0及移动速度ν。假设信号传播速度c、信标节点位置坐标xi为已知参数，测量噪声方差通过预先训练获得，因此可将上述问题模型表示为以下最小化问题

问题(3)的求解可以采用牛顿迭代法的数值计算方法，但数值计算方法依赖于初始解。若初始解选择不合适，有可能陷入局部最优，下面分别介绍采用线性代数法及凸优化算法的实现过程。

图1 移动节点与信标节点的位置分布示意图

2 线性代数法

线性代数法将上述最小化估计问题转化为线性最小二乘估计问题，将估计值直接表示为代数形式解析解，计算过程较快。为将上述问题转化为线性最小二乘估计问题，将式(3)进行变换，并考虑关系式 di，k＝‖xk-si‖及 d0，k＝‖xk‖，有

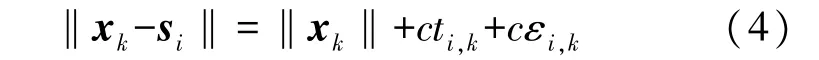
对式(4)左右两边平方，考虑测量噪声εi，k的较小波动范围，忽略二次高阶项，可以得到

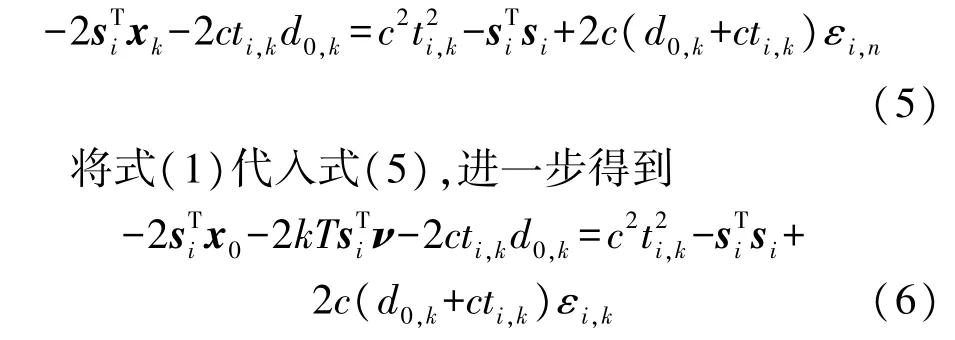
式中:k＝0，1，2，…，K，i＝1，2，…，M。 为将上式表示成矩阵形式，新定义未知向量η＝[νT]T，d0＝[d0，1d0，2… d0，K]T，可将式(6)写为

式中:ai，k＝ [--2k0k-1-2cti，k0K-k] ，-，αi，k＝ 2c(d0，k＋cti，k) εi，k。 按照将 i、k先后递增的次序，将式(7)写成线性矩阵形式

式中:A∈RM(K＋1)×(K＋4)，矩阵 A 的行向量为 ai，k。 b，α∈RM(K＋1)，b 及 α 的行元素值分别为 bi，k，αi，k。 式(8)的加权最小二乘估计可以表示为

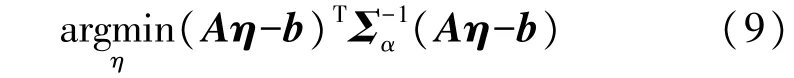
式中:Σα∈RM(K＋1)×M(K＋1)，Σα＝E(αTα)其值表示为

因此根据最小二乘估计原理，未知向量η的估计值表示为

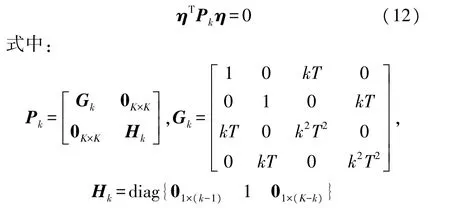
因此可将式(9)表示的加权最小二乘估计表示为

具有约束条件式(13)的问题可以采用拉格朗日乘子法求解，其拉格朗日算子最小化表示为L(η，λk)＝ (Aη-b)Aη-b)＋ λkηTPkη (14)式中:λk为拉格朗日乘子，k＝0，1，2，…，K。 为最小化拉格朗日算子，将L(η，λk)对 η的微分取值为零，即表示为

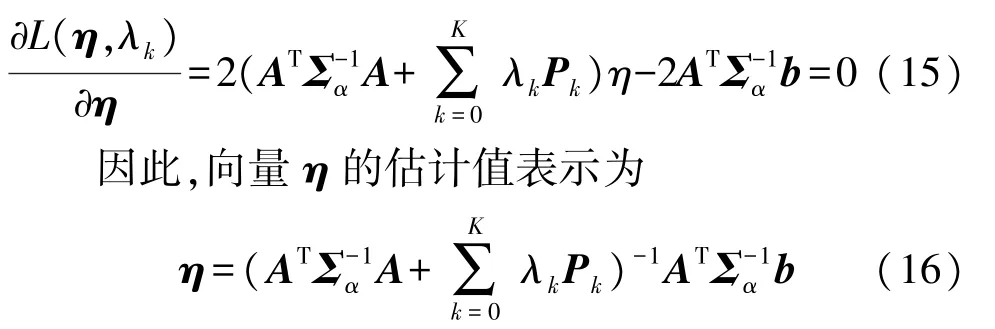
将式(15)代入约束条件，有

式(16)表示的K元方程组难以直接求解拉格朗日乘子λk，若采用数值方法计算，亦极有可能陷入局部最优。为此，下面介绍凸优化方法以实现具有约束条件的问题求解。

3 半正定规划算法

为建立凸优化模型，观察式(7)所建立的等效方程，可将优化问题表示为

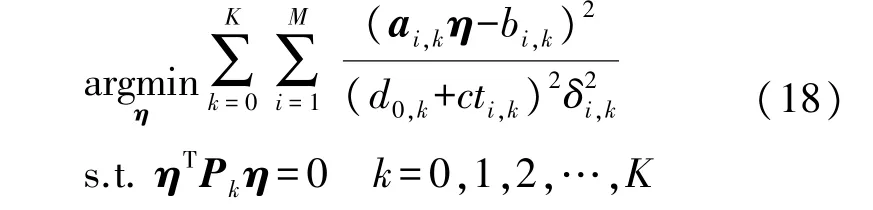
为将上式表示的非凸优化模型松弛为凸优化模型，定义矩阵

故可将约束条件重写为CkZ＝0。定义

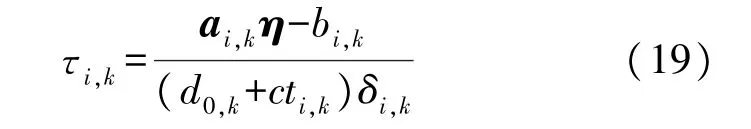
因此优化问题(18)可重新表示为

按照 i、k 先后递增的次序，将τi，k写成向量形式τ，可将优化问题(20)重新表示为

将式(21)中的 Z 松弛为 Z≥0(M＋5)×(M＋5)，并且不考虑rank(Z)＝1，可将优化问题(21)表示为凸优化半定规划(SDP)问题

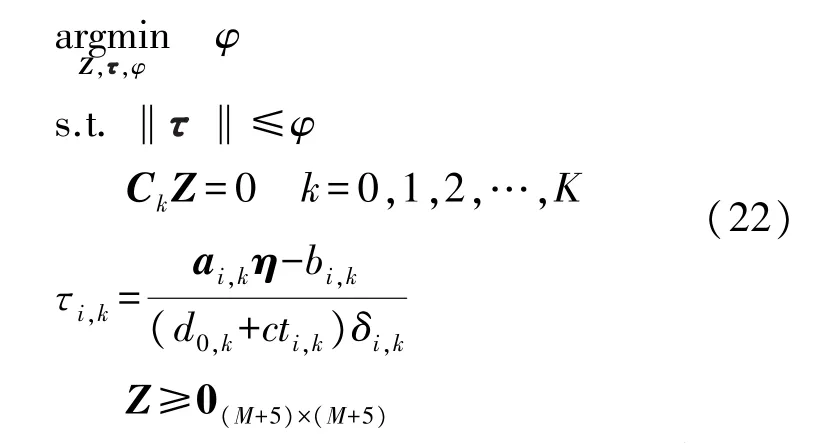
根据矩阵Z的定义，从Z中抽取出相应参数即可得到初始位置x0及移动速度ν的估计值。同式(11)中权重矩阵的计算方法，优化问题(22)中的d0，k初始时为未知值，可预先将权重系数(d0，k＋cti，k)δi，k设置为 1，初步估计 d0，k，然后重新代入问题(22)二次计算精确的估计值。

4 仿真分析

通过移动目标与信标节点间的TDOA测量方法，消除了TOA测量的同向误差，提高了移动目标运动参数估计的可靠性。本验证本文所提出的TDOA-ULLS及TDOA-SDP算法的有效性，将算法与文献[21]的TOA-SDP算法进行了性能比较。采用MATLAB软件，进行了算法的仿真实现。在100 m×100 m的方形区域内将参考信标节点设置在原点，将五个测量信标节点分别设置在(0，100)，(100，100)，(95，60)，(100，0)及(5，60)，并在该区域内随机生成10个移动目标的初始位置。将移动目标沿x轴方向运动速度νx预先设置为0.2 m/s，沿y轴方向运动速度νy预先设置为0.1m/s，性能评价采用10个移动目标的平均估计值进行分析。信号传播速度c设置为3×108m/s，所有的TDOA测量噪声εi，k的噪声方差均设置为 δ2。 为评价所设计算法的估计误差性能，采用均方根误差(RMSE)分析。对每种算法的RMSE估计误差仿真运行1 000次，采用1 000次运行结果的平均值分析。

图2 同向误差对估计误差的影响

4.1 同向误差对估计误差的影响

TDOA的到达时间差测量方法消除了时间测量的同步误差，有利于提高估计性能。而同向误差对TOA方法的影响较大，仿真首先测试了同向误差对文献[21]TOA-SDP算法的影响，并与本文的TDOA算法进行了比较。设置采样周期T为1 s，采样点数量K等于10，时间测量噪声δ为5 ns，图2绘出了本文的TDOA-ULLS及TDOA-SDP算法、文献[21]的TOA-SDP算法的RMSE估计误差随同向误差的变化关系。图2(a)所绘出的初始位置RMSE性能显示随着同向误差增加，本文所提出的TDOA-ULLS、TDOA-SDP算法初始位置RMSE估计误差基本没有变化，而TOA-SDP算法的初始位置RMSE估计误差随之直线增加。当同向误差为1 ns时，TOA-SDP算法的初始位置RMSE误差为0.91 m；而当同向误差为10 ns时，TOA-SDP算法的初始位置RMSE误差上升到了1.79 m。当同向误差小于等于5 ns时，TDOA-SDP算法的初始位置RMSE要大于TOA-SDP算法；当同向误差大于等于6 ns时，TDOA-SDP算法的初始位置RMSE就开始比TOA-SDP算法误差小。

图2(b)绘出了速度估计RMSE随同向误差的变化关系。显然由于消除了同向误差，TDOA-ULLS及TDOA-SDP算法的速度估计RMSE基本与同向误差无关。但与初始位置RMSE误差不同的方面在于，TOASDP算法的速度估计RMSE也与同向误差无关。

图3 时间测量噪声对估计误差的影响

4.2 测量噪声对估计误差的影响

随着TDOA时间测量噪声的增加，显然各种算法的估计误差也将增大。将采样周期T、采样点数量K分别设置为1 s、10个，同时调整时间测量噪声δ从1 ns到10 ns之间变化，图3绘出了RMSE估计误差随时间测量噪声的变化关系。由图3(a)可见，随着时间测量噪声的增加，本文提出的TDOA-ULLS、TDOA-SDP算法的初始位置RMSE误差也随之增大。相比于TDOA-ULLS算法，TDOA-SDP算法的RMSE误差更小。比如，当时间测量噪声δ为10 ns时，TDOA-ULLS算法的初始位置RMSE误差为2.86 m，而TDOA-SDP算法的初始位置RMSE误差仅为2.53 m。在保持同向误差为一定值时，越小的时间测量噪声将导致TOA-SDP算法估计误差大于TDOA-SDP算法。比如，当同向误差为5 ns，并且时间测量噪声δ小于等于4时，TOA-SDP算法估计误差要大于TDOA-SDP算法。同样地，当同向误差上升为10 ns，并且时间测量噪声δ小于等于8时，TOA-SDP算法估计误差会大于TDOA-SDP算法的估计误差。

当时间测量噪声δ从1 ns到10 ns之间变化，图3(b)绘出了速度估计RMSE随时间测量噪声的变化关系。由该图可见，随着时间测量噪声的增加，各种算法的估计误差亦随之增大。比如，当时间测量噪声δ为1 ns时，TDOA-SDP算法的速度估计RMSE为0.039 m/s。而当时间测量噪声δ为10 ns时，TDOA-SDP算法的速度估计RMSE达到了0.365 m/s。当存在时间同向误差时，TOA-SDP算法的速度估计RMSE误差也随测量噪声的增大而增加。但是同向误差对速度估计RMSE的影响有限，这与图2(b)所反映的结果一致。比如，保持时间测量噪声δ为10 ns，当同向误差分别为0 ns、5 ns及10 ns时，TOA-SDP算法的速度估计RMSE分别为0.27 m/s、0.29 m/s及0.30 m/s。而TDOA-SDP算法的速度估计RMSE达到了0.36 m/s。由该图可以看出，在10 ns同向误差范围内，TOA-SDP算法的速度估计RMSE总是小于TDOA-SDP算法的估计误差，所以同向误差大小对TOA-SDP算法的估计误差影响有限。

4.3 采样周期对估计误差的影响

实际应用中采样周期T可随机设置，但改变采样周期T将改变移动目标运动轨迹，将影响估计误差性能。保持时间测量噪声δ等于5 ns及采样点数量K等于10，仿真测试了不同采样周期T对两种估计误差的影响。当采样周期T从0.5 s增加到5 s时，图4(a)绘出了各种算法的初始位置RMSE估计误差随采样周期T的变化关系。由该图可见，各种算法的初始位置RMSE随采样周期T的增加而基本没有变化。当采样周期T等于0.5 s时，TDOA-SDP算法的初始位置RMSE误差为1.26 m；当采样周期T增加到5 s时，该算法的RMSE误差为1.28 m。当同向误差为10 ns，TOA-SDP算法的初始位置RMSE误差大于其他算法的估计误差。

采样周期对初始位置RMSE估计误差影响不大，但对速度估计误差的影响较大。图3(b)绘出了各种算法的速度估计RMSE误差随采样周期的变化关系。由该图可见，各种算法的速度估计RMSE误差都随着采样周期T的增大而减少。比如，当采样周期T等于0.5 s时，TDOA-SDP算法的速度估计RMSE误差为0.37 m/s；而当采样周期T达到5 s时，TDOA-SDP算法的速度估计 RMSE误差仅为0.037 m/s。由分析可知，速度估计RMSE误差与采样周期T有近似成反比关系。增大采样周期T有助于减少速度估计误差，但同时将增加移动目标的运动距离，有可能导致运动距离过大而无法实现与移动目标间的时间测量，这在实际应用时需要注意。

图4 采样周期对估计误差的影响

4.4 采样点数量对估计误差的影响

采样点数量K越多，测量信息越多，当然各种算法的估计误差将越小。保持采样周期T为1 s，时间测量噪声δ等于5 ns，仿真测试了采样点数量K从10个增加到19个时各算法的估计误差性能。图5(a)绘出了各算法的位置估计RMSE误差随采样点数量K的变化关系。由该图可以看出，随着采样点数量K的增加，初始位置RMSE估计误差有所减少。比如，当采样点数量K由10增加到19时，TDOA-SDP算法的初始位置RMSE估计误差从1.23 m减少到了0.87 m。同样地，其他各种算法的初始位置RMSE估计误差也随采样点数量K的增加而减少。

同样将采样点数量K从10增加到19，图5(b)绘出了各种算法的速度估计RMSE随采样点数量K的变化关系。由该图可以看出，随着采样点数量K的增加，RMSE速度估计误差明显减少。当采样点数量K等于10时，TDOA-ULLS、TDOA-SDP与 TOA-SDP(同向误差为0 ns)三种算法的速度估计RMSE误差分别为 0.22 m/s、0.19 m/s、0.14 m/s；而当采样点数量 K增加到19时，三种算法的速度估计RMSE误差分别减少到了 0.08 m/s、0.07 m/s、0.05 m/s。 随着采样点数量K的增加，估计误差减少，性能有所提高。

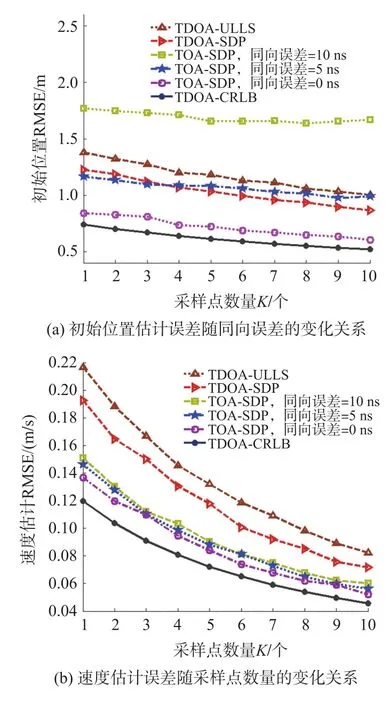
图5 采样点数量对估计误差的影响

5 结论

采用移动目标与信标节点间的TDOA测量方法，消除了时间测量同向误差，减少了移动目标运动参数的估计误差。本文通过建立基于TDOA方法的运动参数估计模型，并设计了TDOA-ULLS的线性代数法，TDOA-SDP的凸优化方法以实现运动参数包括初始位置及运动速度的联合估计。由于考虑了优化模型的约束条件，凸优化的TDOA-SDP算法的初始位置估计误差较TDOA-ULLS算法的估计误差小，但凸优化方法的计算复杂度较高。仿真结果发现，TDOA方法可以有效消除时间测量同向误差，提高初始位置估计精度。增大采样周期可有效减少速度估计误差。采用更多的采样点数量也可以减少RMSE估计误差，但测量成本和难度加大。并且增大采样周期及采样点数量意味着移动距离的延长，有可能导致移动距离较长而无法实现时间测量。