基于模糊核稀疏先验正则化图像盲复原处理

胡双年，李艳艳，牛玉俊

(1.南阳理工学院 数学与统计学院,河南 南阳 473004；2.南阳理工学院 电子与电气工程院，河南 南阳 473004)

在获取图像的过程中，由于相机抖动、景物运动以及散焦等原因，造成图像模糊，从而使图像信息丢失[1-2]. 图像恢复一直是图像领域内的研究热点之一[3-4].常用的去模糊算法主要分为两大类：第一类是图像非盲复原算法[5]，即先将模糊图像视为清晰图像和模糊核的卷积，然后通过已知的模糊核进行反卷积运算求得清晰图像[6-7];第二类是图像盲复原算法[8],即在模糊核未知的情况下，估计出清晰图像[9],常通过添加稀疏先验正则项来进行获取模糊核. Krishnan等[10]通过添加L0正则项来约束图像模糊核的稀疏性，提出了一个新的L0正则约束的方法估计清晰图像，但该优化模型的时间复杂度过大. Xu等[11]利用图像的稀疏性通过添加图像梯度L0正则项提出了去除运动模糊的一个新框架.Cao等[12]利用图像深度作为先验信息来进行盲复原，这些方法虽然能快速得到复原结果，但算法本身对噪声十分敏感. 方帅等[13]利用图像梯度1范数与2范数的比值来模拟图像梯度的0范数，很好地抑制了噪声对图像的影响，得到了比较理想的结果.

论文通过对Krishnan等[10]提出的模糊核估计方法进行改进，利用梯度的0范数作为正则项对以往的算法进行改进. 在求解优化模型的过程中，使用半二次分解法来简化问题，同时提高了模糊核估计的准确性[14-17]. 在反卷积过程中，采用L0.5正则项的超拉普拉斯分布[14]进行运算，从而对模糊图像进行了复原.

1 图像退化基本原理

图像的模糊过程可以视为空间线性不变系统和噪声模型的卷积运算过程，如图1所示.

图1 图像退化模型

图像退化过程中的输入输出关系可以表示为

B=k⊗L+η，

其中：B表示模糊图像，k表示模糊核，L代表原始图像，⊗表示卷积运算，η表示噪声.

从上式可知，可以通过估出模糊核，再通过反卷积运算估计出原始图像. 因此，论文的图像复原过程分为以下两步：

(1) 利用正则化方法估计图像的模糊核；

(2) 利用估计出来的模糊核，采用超拉普拉斯先验分布的正则化方法求解清晰图像.

2 基于模糊核稀疏性L0正则化去模糊算法

L0范数是评价图像稀疏性的一种标准. 论文基于清晰图像的梯度L0范数、模糊核的L0范数较小等，构建了包含梯度和模糊核正则项的优化函数

(1)

式(1)中的第一项是使恢复后的图像和原模糊图像尽可能地相似，第二项是用来保持图像的梯度特征，第三项是用来正则化模糊核.L0范数[15-16]目前无法通过常规数学手段求出其准确值，因此，论文采取半二次分解法求其近似解.

(i) 更新k，固定I，求解k，即

针对k的求解，由于L0范数的非线性，引入变量l，使用半二次分解法进行求解，构造下式

其中:x，y表示权值系数. 上式可以分解为

(2)

(3)

式(2)类似的求解方式有最小二乘法，其图像梯度与模糊核为卷积运算，可以利用快速傅里叶变换的方法求解该问题.

式(3)是逐像素最小化问题[16]，可求得闭合解

最后，交替求解得到k的值.

由于退化图像可以视为原始图像和模糊核进行卷积运算来得到，在模糊核已知的情况下，图像去模糊过程即可视为对退化图像和模糊核进行反卷积运算.由文献[14]可知超拉普拉斯分布能够拟合图像的梯度分布. 因此，在反卷积过程中，采用L0.5为正则项的超拉普拉斯分布进行反卷积运算，获取清晰图像.

3 实验结果与分析

论文在Intel i7处理器、64位win10系统PC笔记本上进行测试. 与领域内的Krishnan[10]、Cao[12]和方帅[13]进行比较，分别在自然图像、人脸图像和文本图像上进行了实验对比，并且利用了PSNR(peak signal to noise ratio)和SSIM(structural similarity index)来进行定量分析.

在获取自然图像的过程中，由于大气粒子散射或相机焦距不易对齐等原因，造成图像不够清晰. 图2和表1分别展示了自然图像的结果对比.

图2 自然图像的实验结果对比图

表1 自然图像的PSNR和SSIM值的对比

方法PSNRSSIMKrishnan53.210.77Cao50.900.80Our57.310.81方帅58.930.79

图2给出了不同算法的对比结果，通过观察可以发现，与Krishnan算法相比，论文的最终结果较为清晰，尤其体现在对物体的细节边缘处理方面. 与Cao和方帅的结果相比，图像整体噪声严重且在局部颜色失真.

人脸图像包含丰富的信息，如年龄、种族、情绪等，其清晰化广泛应用于身份认证等领域. 相较于自然图像，人脸图像有其固定的特征. 论文也在人脸图像做了测试. 图3和表2分别展示了人脸图像的结果对比.

图3 人脸图像的实验结果对比图

表2 人脸图像的PSNR和SSIM值的对比

方法PSNRSSIMKrishnan53.420.76Cao49.700.75Our54.930.81方帅51.830.79

通过实验结果可知论文算法和Krishnan、Cao和方帅的算法相比，去模糊效果明显，在一定程度上保留了图像细节信息，主要体现在面部少褶皱、皮肤光滑、清晰度高.

文本图像和其他图像相比，有其自身独特的特点，如非文字区域的梯度明显大于文字区域. 所以针对文本图像的去模糊有着重要研究意义. 图4和表3展示了文本图像的结果对比.

图4 文本图像的结果对比

表3 文本图像的PSNR和SSIM值的对比

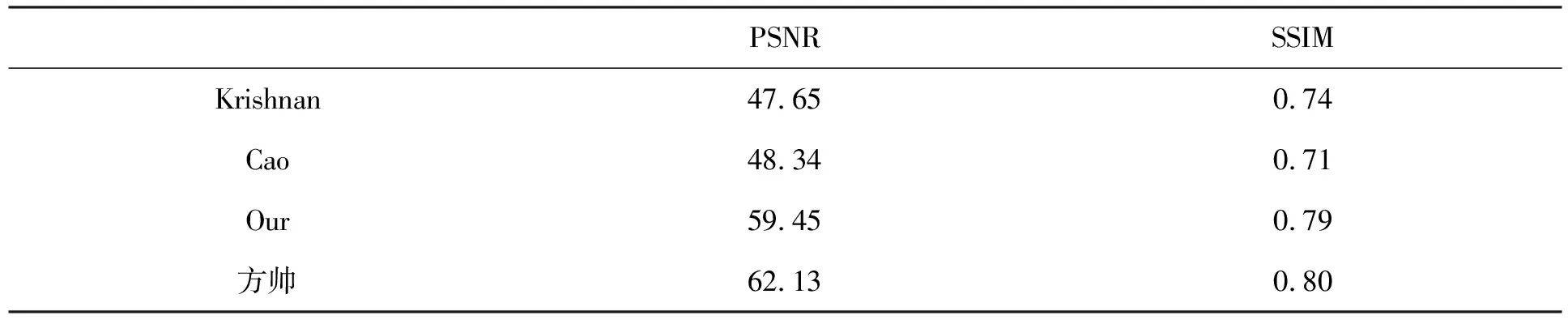
PSNRSSIMKrishnan47.650.74Cao48.340.71Our59.450.79方帅62.130.80

通过观察发现论文结果的清晰度明显好于Krishnan、Cao和方帅的结果，文字的边缘处清晰，几乎没有模糊的痕迹.Krishnan虽然也取得了不错的结果，但是与论文算法也有一定差距. 而Cao和方帅的结果可以发现边缘处仍然有点模糊，图片呈现效果不佳.

修复速度也是评价算法的一个重要指标，故论文同时统计了10幅大小300*400图像的处理时间，如表4所示.

表4 运算时间的比较

4 结束语

论文根据图像的退化原理，采用图像梯度的L0范数和模糊核的L0范数构建优化函数，保证了模糊核的准确性.同时引入了半二次分解法来解决L0范数难以求解的难题.在反卷积中，采用文献[14]描述超拉普拉斯分布拟合图像的梯度分布，利用L0.5为正则项的超拉普拉斯分布进行反卷积运算，最终获得了较为清晰的图像. 论文通过在不同种类图像上进行测试，如自然、人脸和文本图像，都取得了较好的结果，同时利用PSNR和SSIM进行了定量描述. 但论文方法采用的卷积模型，只有在整幅图像都具有同一模糊核才能取得较好效果，这是论文的局限所在. 对于局部模糊图像，由于其各区域的模糊核是不一致的，论文方法的效果不太理想，但这也是作者下一步研究的方向.