优化极限学习机算法及其在力信息解耦中的应用∗

徐家琪，伍万能，2，孙 炜，2，3，王耀南，2，梁桥康，2，3∗

(1.湖南大学电气与信息工程学院，长沙410082；2.机器人视觉感知与控制技术国家工程实验室，长沙410082；3.电子制造业智能机器人湖南省重点实验室，长沙410082)

多维力传感器在机器人柔顺操控与智能作业等方面承担了重要的感知作用[1]。其检测精度的提高有助于实现更精确有效的力觉控制。解耦算法的性能对多维力传感器的检测精度有极大的影响[2]。近年来，以机器学习为核心的人工智能算法研究得到了飞速发展。许多机器学习方法因其优异的性能被应用到多维力传感器的解耦中。其中，韩彬彬[3]利用遗传算法优化BP神经网络，并以此融合算法对压电式六维力传感器进行解耦，解耦效果表明融合解耦算法对传感器测量性能有显著提高。石中盘等[4]利用混合递阶遗传算法优化小波神经网络并以此进行多维力解耦，实验结果表明，该优化算法的精度较其他常见的非线性解耦方法有明显优势。

尽管神经网络在力解耦方面表现出较好的解耦性能，但是解耦精度仍有待进一步提高。同时，常用的神经网络存在解耦时间长的问题，使得解耦效率较低。本文旨在设计具有更高解耦精度与更高效率的解耦方法的多维力信息解耦算法。

Guangbin Huang等人于2004年提出了一种基于前馈神经网络的高效机器学习算法——极限学习机(Extreme Learning Machine，ELM)。 相比于神经网络，极限学习机的特点在于其输入层与隐含层的神经元权值参数与阈值参数是随机给定或者人为给定的，在学习过程中无需调整，仅需要通过合适的算法计算隐含层与输出层之间的权重。极限学习机具有较高的学习效率、准确度、泛化能力和学习能力，因此被广泛应用于机器学习的分类、聚类和回归等各个环节。

尽管极限学习机训练快且具有较强的泛化能力，但是常常存在优化不足与复共线性的问题，使得模型预测结果不够稳定。因此，诸多优化算法不断被应用于极限学习机中(如表1所示)，常见的有粒子群算法(Particle Swarm Optimization，PSO)和遗传算法(Genetic Algorithm，GA)。李婉华等[5]设计了基于粒子群算法优化的并行极限学习机，用于处理大规模电力预测，与真实电力负荷预测结果对比可知，改进的极限学习机具有较高的稳定性与可扩展性。针对极限学习机随机产生的输入值权值与隐含层阈值容易导致网络结构不稳定的问题，律方成等[6]提出利用遗传算法对极限学习机进行改进，并将其应用到短期电力负荷预测中，实验结果表明，其模型具有较快的训练速度与更精确的预测结果。

表1 极限学习机优化算法

本文提出基于天牛须优化算法的改进极限学习机算法(BAS-ELM)，利用天牛须优化算法对极限学习机随机产生的输入层与隐含层之间的权值与阈值进行优化计算，并将其应用于多维力传感器的解耦，通过多维力传感器的解耦实验，逐一比较各个优化算法对极限学习机的改进效果。

1 极限学习机理论及其改进算法理论

1.1 极限学习机

极限学习机是一种新型的单隐层前向传播神经网络的高效机器学习算法，仅包含一个隐含层，其以广义逆矩阵理论作为理论依据，具有很强的非线性拟合能力[10]，由于仅存在一个隐含层且输入层与隐含层之间的权值与阈值是人为给定或者随机得到的，其训练速度极快，其网络结构如图1所示。

极限学习机第j个输入信息Xj对应的输出数据为Yj，二者关系可以表示为:

图1 极限学习机结构示意图

式中:g(X)是激活函数，Xj是第j个预测数据，w1i是输入层与隐含层之间的权值的第i列，bi是第i列隐含层偏置，βi是隐含层第i个神经元到第j个输出值得权值，表示内积。

极限学习机算法常使用Sigmoid函数作为隐含层的激活函数，其可以表示为:

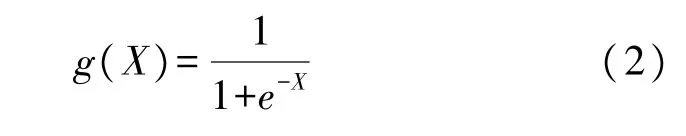
在极限学习机的网络结构中，输入层与隐含层之间的权值w1m×s与阈值 b11×s可以通过随机选取或者人工设定；而隐含层与输出层权值βs×x可以通过最小二乘法进行确定，最小二乘法的计算公式如下:

式中:H为隐含层通过激活函数后的输出值，其运算公式为:

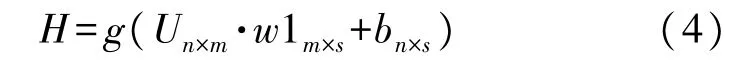
式中:bn×s是阈值 b11×s复制 n行后的整体阈值矩阵。

1.2 天牛须算法

天牛须优化算法是一种模拟自然界天牛行为的优化算法，其求取最优解的方式是通过模拟天牛寻找食物的过程而完成的。天牛通过头上两只触角接收食物的气味，根据触角接收到的气味方向行走一段距离[11]。参数自变量X代表天牛当前的位置，参数自变量X的最优解相当于食物的位置，参数自变量xi按照一定方向增加或减少相当于向左走向右走，当参数自变量X达到最优解时，目标函数便求得了最小值或者最大值。

当利用天牛须算法进行最优解运算时，首先初始化参数自变量X，然后按照正态分布初始化向量dir，之后使得参数自变量X按照向量dir进行增加或者减少，得到X_left和X_right，通过判断X_left和X_right对应的目标函数的值，判断参数自变量X下一步应当走的方向。

2 基于天牛须的改进极限学习机(BAS-ELM)

利用天牛须算法对ELM训练过程中随机产生的输入层与隐含层之间的权值与阈值进行优化，在确定ELM的隐含层神经元数量后，其优化过程如下:

(1)对天牛须优化算法的参数进行初始化，需要初始化的参数分别有衰减率Δ、比率c、最大起始步长step，迭代次数n等。

(2)初始化N维参数自变量X，N由神经元的个数与输入量的维度决定，其计算公式如(5)所示。通过目标函数的定义，求取其对应的函数值F(X)。

(3)以正态分布的方式获得每一维自变量xi在每次迭代的过程中变化的方向向量dir。

(4)X向量通过利用第3步获得的dir向量实现“向左迈进一小步”。

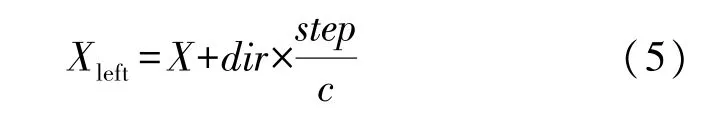
其对应的函数值为F(Xleft)。

(5)X向量通过利用第3步获得的dir向量实现“向右迈进一小步”。

其对应的函数值为F(Xright)。

(6)比较F(Xleft)和F(Xright)的大小，并以此来判断X应当往某一方向走一大步。公式如下:

如果F(Xleft)大于F(Xright):

(7)按照迭代次数n，重复步骤3到步骤6，求取最优解。

3 改进ELM在多维力解耦中的应用

3.1 应用背景

多维力传感器可以同时测量多个方向的力与力矩。由于其弹性体一体化结构设计不足、制造工艺和贴片水平的限制，当某个方向的力被加载到传感器上时，其他方向也有一定的耦合输出。这种耦合问题难以通过结构优化而实现，软件解耦相对于结构优化解耦而言实用性更高。

由于力传感器各维度之间的结构耦合呈现出严重的非线性，对机器学习的模型及其优化方法要求较高，普通的模型难以取得良好的效果。

3.2 评价方法

本文以文献[12]中所述的误差率和预测结果的损失函数为主要评价指标，误差率的定义如下:

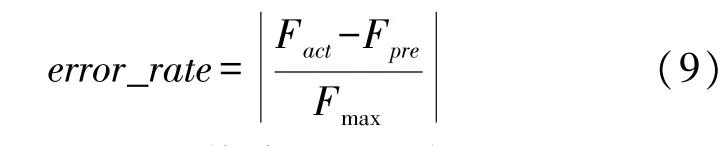
式中:Fact为实际加载到传感器上的各方向力与力矩的大小，Fpre为解耦算法运算得到的力与力矩的值，Fmax为满量程值。

本文使用的预测结果的损失函数的定义为:

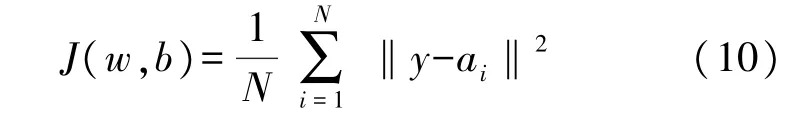
式中:ai＝f(w·x＋b):x是输入值、w为网络权值、b为网络参数、f(z)是激活函数，J(w，b)反映的是均方误差(Mean-Square Error，MSE)。

4 解耦实验

4.1 解耦数据的获取

本文的解耦数据由团队开发的六维力/力矩传感器标定实验获得。通过标定实验，可以获得大量六维力/力矩传感器在受力状态下，输入力/力矩大小与输出电压的对应样本。本文共获得354个数据样本，将这些数据样本进行训练集与测试集的划分，共获得训练集300个，测试集54个。

4.2 算法参数的选取

4.2.1 ELM算法参数的选取

本文通过测试集在ELM处于不同神经元个数时，损失函数的变化，寻找ELM的过拟合点。

由图2可知，当ELM算法神经元大于130个时，损失函数不再下降，甚至由于过拟合存在上升波动。因此本文选择神经元个数为130。

图2 ELM神经元个数与损失函数的关系

4.2.2 PSO-ELM算法参数的选取

在PSO-ELM算法中，按照经验，本文将个体学习率c1和社会学习率c2设置为2，每个粒子群的大小ParticleSize设置为30，最大速度Vmax设置为5，惯性w设置为0.8。

在GA-ELM算法中，将交叉和变异概率设置为0.5和0.01，种群大小设置为30。

在BAS-ELM算法中，将衰减率设置为0.997(在经过300次迭代后，步长变为原来的0.406倍)，比率设置为5，最大起始步长设置为1。

对于优化算法的迭代次数而言，其与训练时间相关，次数过多会导致训练时间过长；次数过少会导致训练不完全，精度低。本文通过训练集的损失函数随迭代次数的变化，得到各个优化算法的最佳迭代次数。

由图3可知，当 PSO-ELM、GA-ELM、BAS-ELM迭代次数分别大于60、40、200时，损失函数不再明显下降，由此确定各个算法的迭代次数。

4.3 实验结果

将各类改进的ELM在测试集上进行解耦测试，得到的测试结果的Ⅰ、Ⅱ类误差、损失函数和解耦时间，并通过这些参数来比较各类改进ELM的优缺点。

当某一方向力单向加载时，利用各类改进解耦方法对测试集进行测试，每个方向的误差率如表2所示。

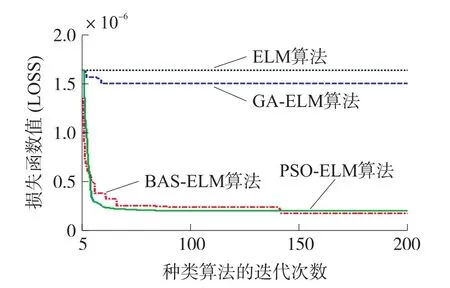
图3 PSO-ELM迭代次数与损失函数的关系

表2 各解耦方法在单向加载时的最大误差率

根据表2可以得到某方向力单向加载时，各方向Ⅰ类误差最大值和各方向Ⅱ类误差最大值，如表3、表4所示。

由表3可知，普通的ELM算法在各个方向上的Ⅰ类误差得到了一定的控制，保持在1.4%以内；GA-ELM算法相对于普通的ELM算法，性能有一定的提升，各方向Ⅰ类误差保持在1.1%以内；PSO-ELM算法和BAS-ELM算法相对与其他两种算法，解耦性能优秀，各方向Ⅰ类误差均保持在0.1%以内。

表3 各方向Ⅰ类误差最大值 单位:%

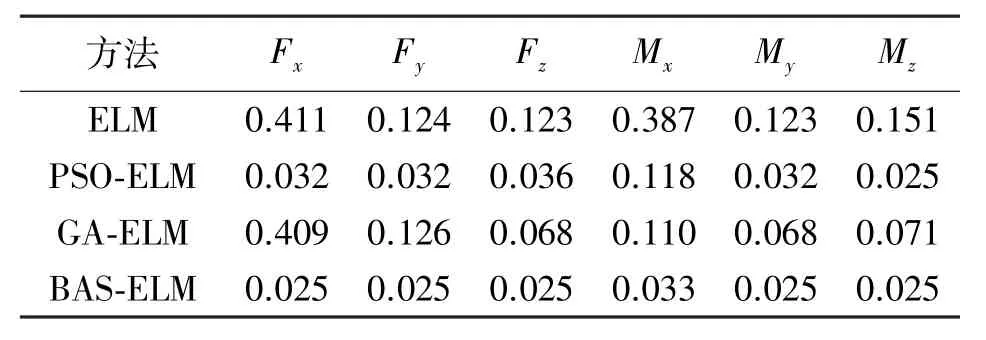
表4 各方向Ⅱ类误差最大值 单位:%

由表4可知，普通的ELM算法在各个方向上的Ⅱ类误差保持在0.5%以内；在Ⅱ类误差的控制上，GA-ELM算法相对于普通的ELM算法有一定提升，但不明显，Ⅱ类误差同样保持在0.5%以内，各方向Ⅰ类误差保持在1.1%以内；PSO-ELM算法和BASELM算法相对与其他两种算法，解耦性能更优，其中PSO-ELM的Ⅱ类误差保持在0.12%以内，BASELM的Ⅱ类误差保持在0.05%以内。

表5 各类方法的最小损失函数值

由表5可知，GA-ELM算法的性能相对于普通ELM算法有一定提升，但效果不明显。PSO-ELM算法和BAS-ELM算法相对于其他算法有较为明显的提升，在最小损失函数上BAS-ELM算法表现略优于PSO-ELM。各类解耦方法对应的训练时间如表6所示。

表6 各类解耦方法的训练时间

由表6可知，ELM算法的解耦时间非常快。在利用优化算法对ELM进行优化后，GA-ELM训练时间较长，其训练时间长与其基因需要用二进制编码导致基因长度较长有关。PSO-ELM算法使用粒子种群进行运算，运算量较大。相对于其他优化ELM算法，BAS-ELM解耦算法的训练时间较短。

4.4 实验结果分析

从表7的结果对比并结合上文内容，可知:

(1)极限学习机及其优化算法具有运算时间短，解耦性能高的特点。

(2)GA-ELM解耦算法训练时间长，性能相对普通ELM有一定提升但提升有限。

(3)PSO-ELM算法性能表现极好，但解耦时间相对于BAS-ELM和普通极限学习机有一定的上升。

(4)BAS-ELM算法在保持优良性能的情况下，解耦时间也得到了一定的控制，实现过程相对于其他改进算法更加简单。

表7 实验结果分析

5 结论

本文在基于粒子群算法和遗传算法的改进极限学习机基础之上，提出了基于天牛须算法的改进极限学习机算法(BAS-ELM)，并将其应用于智能机器人多维力/力矩传感器的解耦实验中。实验结果表明，GA-ELM解耦算法训练时间长，性能提升有限；PSO-ELM解耦算法性能表现极好，但训练时间相对ELM和BAS-ELM较长；BAS-ELM解耦算法在保持优良性能的前提下，缩短了训练时间，同时实现过程相对其他算法简单，具有实际的应用价值。