斜交箱梁桥荷载横向分布系数的简化计算方法
(天津渤海职业技术学院,天津 300408;中国铁路设计集团有限公司,天津 300142)
城市立交里面,箱梁是常见的一种型式并且被广泛使用。和正交相比,斜交梁桥的空间受力状态、受力机理比正交复杂得多,斜交梁桥所表现出来的力学特性,主要包括弯扭耦合效应、反力分布不均匀、以及跨中弯矩折减。正桥横向分布系数求解简单易行,但是斜交桥在此方面却不那么容易,因为其影响因素包含多方面,比如斜交角、宽跨比、抗弯扭刚度以及支撑方式、荷载型式。如此看来,探究荷载横向分布系数简化算法的准确、便捷性显得尤为重要。主要方法归结起来就是:杠杆原理法、刚性横梁法(偏心压力法)、铰(刚)梁板法、以及G-M法;空间数值法包含空间梁单元法、板壳元法、三维实体元法和梁格法;针对斜交板桥与斜交梁桥一般采用空间数值解法,如何寻求一种计算斜交梁桥荷载横向分布系数的简便算法就显得尤为迫切和有意义。文献提出用模态参数法计算桥梁荷载横向分布系数,主要是利用模态柔度的概念,并且这种方法不受桥梁类型的约束。本文在此基础上以某匝道桥为例,进一步验证了模态参数法的可行性与适用性。
一.理论依据
1. 影响线与荷载横向分布系数
影响线的定义,在单位移动荷载P=1下,结构某量值Z的变化特征用函数图像代表,即该量值的影响线。荷载横向分布系数,用来求解某梁k点截面内力,可依据该梁荷载横向分布影响线。对于汽车荷载的横向分布系数m,其公式如下:
⑴
式中:ηq——对应于汽车荷载集度的荷载横向分布影响线竖标。
2. 计算方法介绍
用模态参数法求解荷载横向分布系数原理,就是通过主梁挠度横向分布规律,来确定横向分布系数。计算时要先得到模态柔度;然后依据算出的模态柔度,提取各片梁在跨中的变形值;求出荷载位置处影响线竖标值,依据公式⑴得出所要求解的系数。模态参数法中,t时刻的位移向量用模态振型表达如下:u(t)=q1(t)φ1+q2(t)φ2+…+qp(t)φp=ΦQ(t)
⑵
式中:qi(t)——结构的广义坐标;
φi——第i个模态振型;
Φ——p阶模态振型矩阵;
Q(t)——广义模态贡献列向量。
我们知道,低阶模态的贡献大于高阶,则取前r阶计算,上式⑵可以表示为
⑶
式中:cj,i——模态系数,表示第模态振型对第柔度的贡献程度;
λi——第i个模态的特征值;
mi——第i个模态质量;
式⑶物理意义,指第j自由度作用单位荷载的情况下,产生静态位移的模态近似。
经推导得到任一梁号影响线竖标值,以j梁为例,其公式为
⑷
综合上述各公式,按照模态参数法求解荷载横向分布系数的步骤是,先计算得到固有频率和模态振型,然后按式⑶计算跨中截面各梁中心位置的模态柔度,再按式⑷计算其影响线竖标值。
文献在研究预制装配式小箱梁这一系数时,通过比较刚接板梁法、刚性横梁法以及比拟正交异形板法(G-M法)后得出结论,在3至5片梁情况下,建议选取刚性横梁法来求解荷载横向分布;而梁数在5至9片时,则建议采用比拟正交异形板法进行计算。然而,上述提到的小箱梁并没有说是否适用于斜交箱梁。文献提出目前对于斜弯桥的计算,常常可以采用刚性横梁法。文献也讨论了刚性横梁法在直交桥、斜交桥、平面弯桥的判别条件,推导了刚性横梁法在各种桥型中,求解横向分布影响线的公式。但是文献就明确提出刚性横梁法并不适用于斜交板桥与梁桥,要计算斜交板桥与梁桥的荷载横向分布系数一般采用空间数值解法。故本文在选取模态参数法的同时,再取用刚性横梁法,并将两者结果进行对比。
二.工程实例
1. 工程背景
某斜交桥斜交角20度,上部为单箱三室预应力砼连续箱梁,梁高150cm,梁宽1500cm,顶板厚20cm,底板厚25cm,腹板厚45cm,中间支座处横隔梁宽120cm,端支座处宽为200cm。
该桥设计行车速度采取35kN/h,设计荷载等级为汽车-超20级,挂车-120。桥面宽度形式为0.50 m(护栏)+6.92m(行车道)+0.66 m(中央分隔护栏)+6.92 m(行车道)+0.50 m(护栏)=15.50m。
上部结构用C50预应力混凝土梁,抗压弹性模量Ec=3.45×104MPa,容重γ=26kN/m3,轴心抗压强度设计值fcd=22.4MPa,轴心抗拉强度设计值ftd=1.83MPa。桥面系中防撞护栏容重值γ=26kN/m3,沥青混凝土容重24kN/m3。箱梁横截面图见图1。
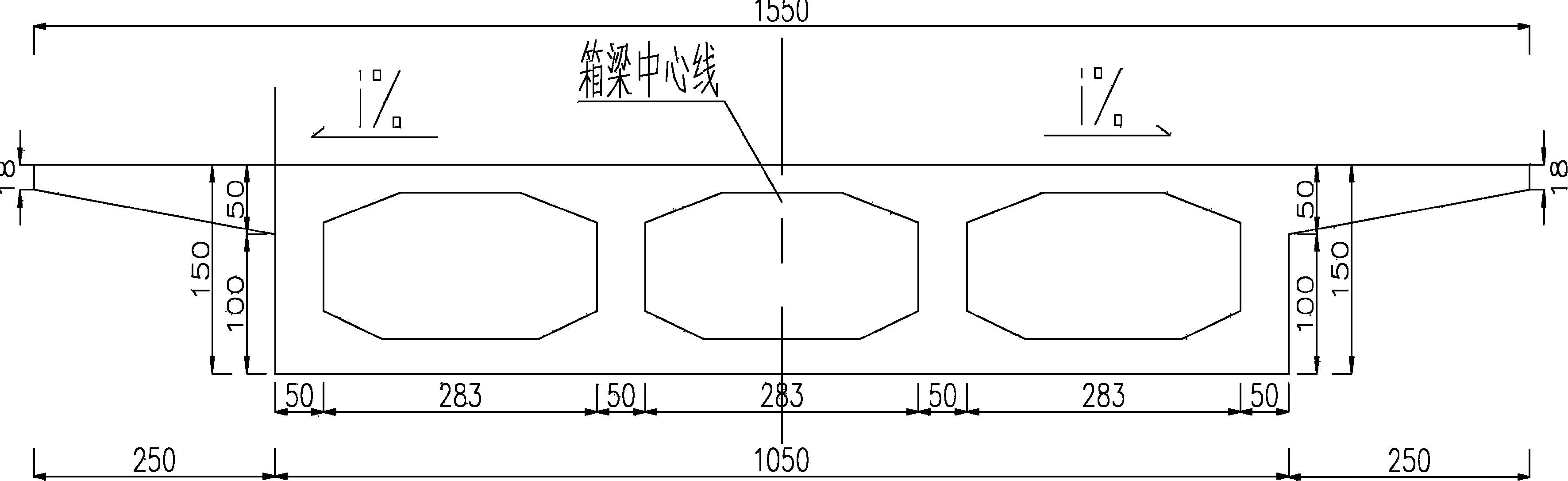
图1 箱梁横截面图(单位:cm)
2. 模型建立与结果分析
通过有限元程序Midas civil 2012进行求解分析,梁格法确立上部结构有限元模型,总共划分532单元,333节点。同时,把沥青混凝土铺装层、防撞护栏质量,以每延米质量来表示,得到结构振动基频如见表1和该模型第一阶振型见图2。

表1 固有频率
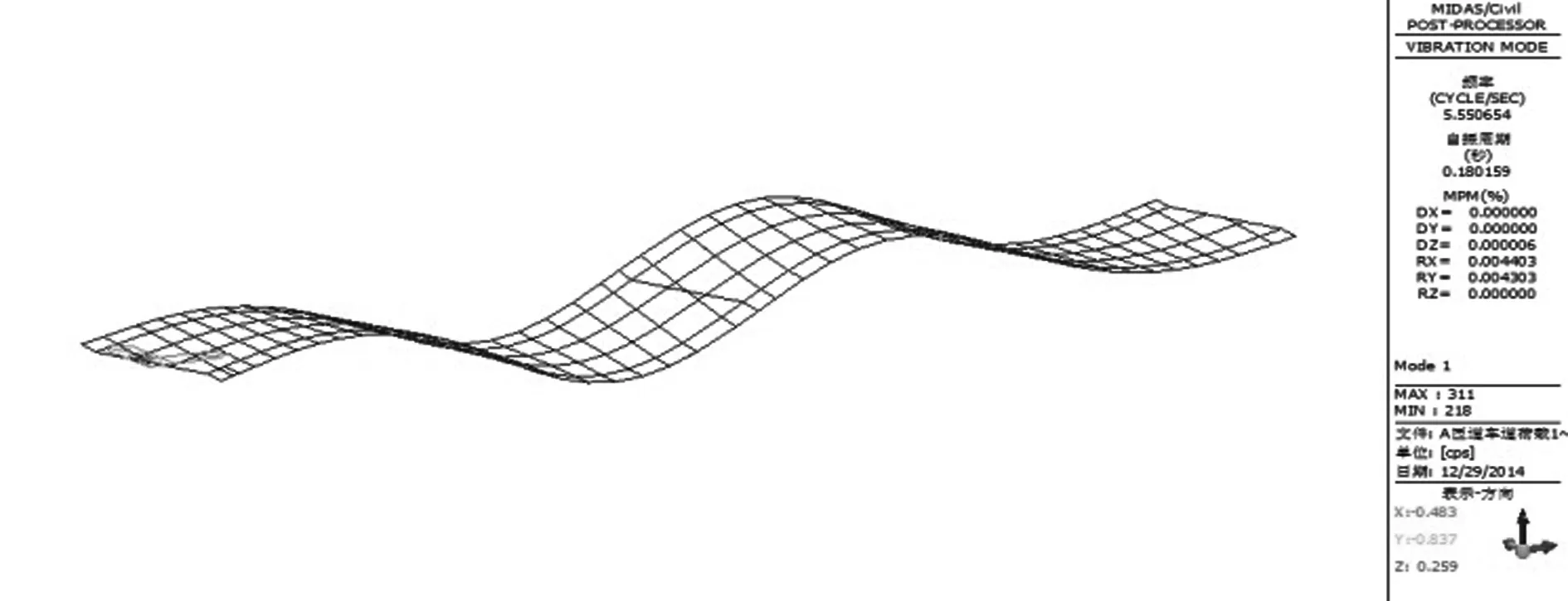
图2 第一阶振型(竖弯)
利用上述模态参数法、刚性横梁法,求解荷载横向分布系数,结果见表2及图3。

表2 荷载横向分布系数
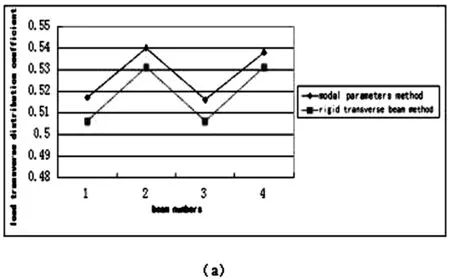
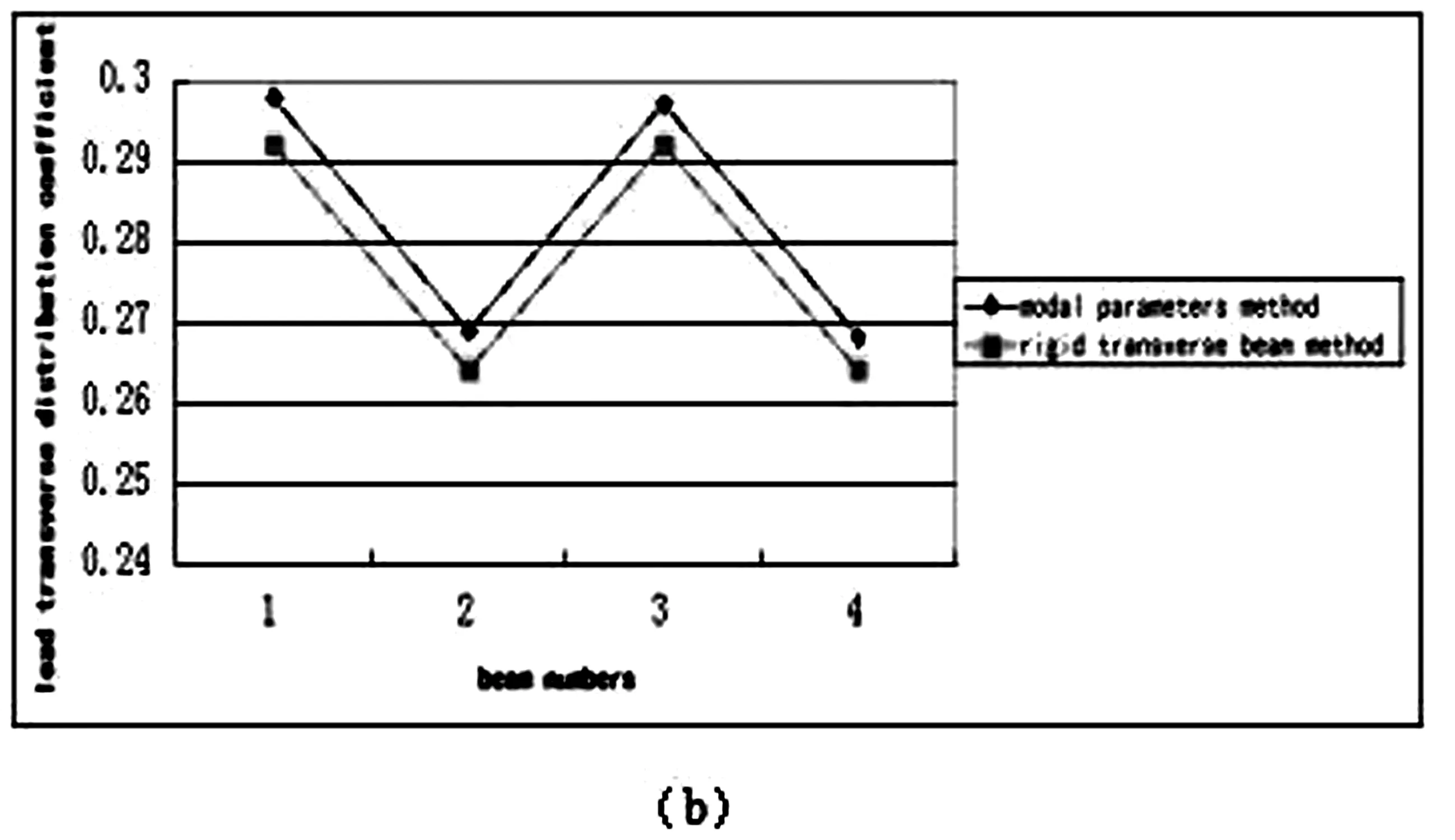
图3 (a) 汽车-超20荷载下横向分布系数变化图
表1给出了该斜交箱梁桥在汽车-超20级、挂车-120作用下,采用模态参数法和刚性横梁法的结果,并且给出了两者偏差大小。从上述结果可以看出,模态参数法与刚性横梁法,用于求解荷载横向分布系数时基本变化规律相同,且模态参数法数值偏大;汽车-超20级荷载和挂车-120荷载下的横向分布系数值变化规律相同,最大误差均不超过5%,能满足工程实际的需要。
三.结论
其一,本文基于结构动力学的知识,提出可以应用模态参数法,求解斜交桥梁的荷载横向分布系数,并且给出求解公式与步骤。其二,以“化动为静”的思想,将动态域的数据用于求解静态域的问题,采用模态参数法用于求解斜交桥的荷载横向分布系数。其三,以一座斜交箱梁桥为例,将模态参数法结果与和刚性横梁法结果对比后发现,二者最大误差不差过5%,说明模态参数法,可以较好的完成斜交桥梁荷载横向分布系数的计算工作。其四,实际桥梁设计及检测过程中,应加强对模态参数法的关注,以便能更好更快地求解荷载横向分布系数。

