螺旋沟槽参数对纵-扭变幅杆振动分量的影响*

赵 波， 殷 森， 王晓博， 赵重阳

(河南理工大学机械与动力工程学院 焦作,454000)

引 言

随着现代工业的飞速发展，脆难加工材料，特别是金属基复合材料及纳米复相陶瓷加工需求日益增加。超声振动加工技术因其在硬脆材料加工中的突出优势，得到广泛的研究及应用[1]。单一的超声振动模式已不能满足日益复杂的加工要求，超声加工系统的复合振动模式开始得到国内外学者的关注。复合振动模式主要有纵弯复合、扭弯复合[2]、纵扭复合[3]、双弯曲复合[4]及径扭复合[5]等。目前，实现纵-扭复合振动的方式大致可以分为两种:a.通过换能器实现，如利用极化方向不同两组压电陶瓷组成的纵-扭复合振动换能器[6]、利用轴向磁致伸缩产生扭转振动的换能器[7]和将压电陶瓷进行倾斜布置的纵-扭复合换能器[8]；b.通过变幅杆实现，如对其结构进行特殊化设计，在变幅杆上添加“模态转换器”，将纵向振动模式进行转换与复合，如螺旋槽式变幅杆[9]、斜槽式变幅杆[10]及榫卯式变幅杆[11]。

对于螺旋沟槽式纵-扭复合变幅杆而言，其扭转振动分量较高，纵-扭复合振动的输出较为稳定。作为纵-扭复合振动的模态转换器的螺旋沟槽结构，其结构参数的变化会对纵向振动分量及扭转振动分量产生一定的影响，从而改变变幅杆输出端的振动轨迹[8]。笔者利用理论推导、有限元分析与实验验证相结合的方法，探究了螺旋沟槽结构参数对变幅杆的纵向振动分量与扭转振动分量的影响。通过对螺旋沟槽结构参数的合理选择，可实现对扭纵分量比j的调整，从而对超声椭圆振动轨迹进行精确控制。

1 纵-扭模态转换与振动轨迹的理论分析1.1 螺旋沟槽的纵-扭模态转换

图1 圆锥变幅杆上开设螺旋沟槽Fig．1 Helical slots are formed on the conical horn

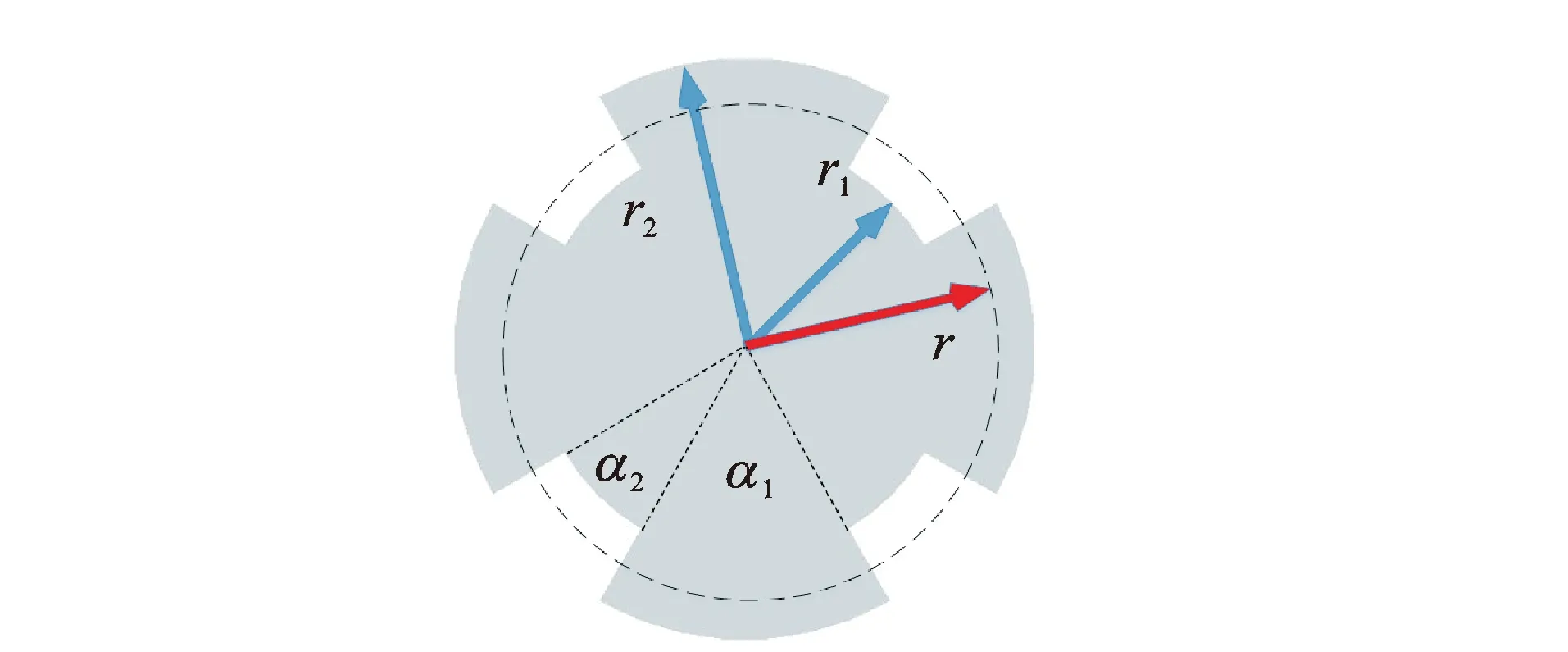
图2 螺旋沟槽切口形状Fig．2 Helical slots incision shape

在一圆锥形变幅杆侧面上开设均布螺旋沟槽，如图1所示。图中：F为纵波产生的纵向惯性力；F1和F2分别为F沿螺旋沟槽分解的力；F2L为纵向作用力分量；F2T为及剪切作用力分量；M为剪切作用力产生的扭矩。结合变幅杆强度要求及机械加工难度，将沟槽设计成类梯形状，沟槽所包络为一实心圆柱，沟槽的长度为变幅杆母线长度如图2所示，图中：r为变幅杆任意横截面的截面半径；r1为实心部分半径，即变幅杆小端半径；r2为变幅杆大端端面半径；α1为相邻沟槽间未切除部分对应的圆心角；α2为沟槽部分对应的圆心角。

纵波在空气介质中传播时，会发生较大的能量损耗，故在纵波倾斜入射螺旋沟槽时，可只计算反射纵波和反射横波的影响，而忽略纵波二次折射所产生的影响[12-13]。纵波产生的纵向惯性力F将分解为F1和F2：在沟槽所包络实心圆柱中的力F1将继续沿纵向传递；在螺旋沟槽结构部分截面上的力F2沿沟槽旋转方向与F成θ夹角。F2将分解成两部分：纵向作用力分量F2L及剪切作用力分量F2T，其中纵向作用力分量沿着变幅杆轴线方向；关于剪切作用力分量，在截面上任一点的剪切作用力分量垂直于半径的方向，由剪切作用力分量产生的总力矩是所有剪切作用力在整个截面上扭矩的积分。

由图1可知，这两个力分量大小可由下式给出

F2L=F2cosθ

(1)

F2T=F2sinθ

(2)

其中：θ为螺旋沟槽的螺旋角。

根据纵向振动及扭转振动理论，纵向力将驱使变幅杆产生纵向振动，而剪切作用力将驱使变幅杆产生扭转振动。剪切作用力产生的扭矩M可以表示为

(3)

由图2可知，变幅杆任意横截面面积s为

(4)

变幅杆任意横截面半径为r处的微分元面积ds为

(5)

变幅杆任意横截面上的剪切作用力f为

(6)

将式(24),(25)代入式(26)可以得到

(7)

其中：r2为变幅杆大端端面半径。

化简并求得

(8)

故由于螺旋沟槽的存在， 可使单向模态的纵向振动激励实现超声纵-扭复合振动的输出。由此式可知:纵向惯性力F由纵振换能器提供，为定值；r1,r2为复合变幅杆尺寸，其也为确定值。

由图1可知

α1+α2=360/n

(9)

其中:n为螺旋沟槽数目。

α1,α2与螺旋沟槽数目n相关，而α2对应的的弦长与螺旋沟槽的槽宽d相关，故扭矩M与螺旋沟槽的数目n，沟槽角度θ及沟槽槽宽d等变量相关，即扭转分量大小与此3个因素的取值有关。

1.2 输出端上质点轨迹分析

前文中分析，螺旋沟槽使得纵振换能器所激励的部分纵振振动转换为扭振振动，而另一部分则直接传递到变幅杆输出端。由于这两种振动在相同介质中的传递路径及传递速度均有不同，故变幅杆输出端上的质点的运动轨迹是在两个频率相同但相位不同的纵、扭振振动的共同作用[8]。

在变幅杆输出端面上取不在轴线上的任意质点P，设un代表质点扭转振动的线位移，uz代表质点沿变幅杆轴线方向的纵向振动位移，则质点P的振动轨迹方程可以表示为

(10)

其中：ω为换能器激励频率；Uz，Un分别为质点P的纵向振动与扭转振动位移振幅；φ为纵向振动与扭转振动的相位差。

对式(10)进行分解，可得

un/Un=sinωtcosφ+cosωtsinφ

(11)

由式(10)可得

uz/UZ=sinωt

(12)

将式(11)代入式(12)中，可得

(13)

整理可得

(14)

从式(14)中可知，当质点P的纵向振动与扭转振动位移的相位差达为φ时，其运动轨迹为一椭圆，且该椭圆轨迹的形状及运动方向与φ的取值有关。当相位差φ为不同的数值时，可以得到如图3所示的各种运动轨迹。

图3 质点在不同位移相位差下的运动轨迹Fig．3 The trajectory of the particle under different displacement phase difference

螺旋沟槽结构作为扭转振动的模态转换器，其转换的纵向振动及扭转振动的分量是相互独立的，因此，质点P不同的纵振振幅与扭转振幅的比值可使其刻画不同的运动轨迹，如图4所示。

图4 椭圆运动轨迹与纵扭两振幅的关系Fig．4 The relation between elliptical motion trajectory and longitudinal and torsional amplitude

由式(8)，(9)可知，使变幅杆发生扭转振动的扭矩M大小与螺旋几何沟槽的参数相关，因此，合理选择螺旋沟槽参数，可改变复合振动中纵向振动分量与扭转振动分量，从而实现对质点运动轨迹的控制。为纵-扭复合超声电机的开发利用提供了参考，对推广纵-扭复合超声振动加工具有重要意义。

2 螺旋沟槽变幅杆的有限元分析

为了同时获得较大的变幅杆放大系数和形状因素，设计圆锥过渡式阶梯型复合变幅杆[14]。选用价格低廉，易加工且疲劳强度较高的45#钢，设计谐振频率为35 kHz的变幅杆，其结构尺寸如图5所示。在其圆锥段开设4条均布的沟槽，形状如图1,2所示，螺旋角度为θ=45°，槽宽为d=8 mm、槽深为h=7.5 mm(以圆锥段大端为基准)。

图5 圆锥过渡式阶梯型复合变幅杆结构尺寸Fig．5 Composite horn structure dimension drawing

利用PRO/E软件对螺旋沟槽变幅杆进行三维建模，并导入有限元分析软件ANSYS中，进行模态分析，网格划分时选取20个节点的solid95单元，采用自由网格，设精度等级为4，模态分析提取方法为Subspace，模态拓展阶数为10，模态搜索设置范围为30～40 kHz。针对切除螺旋沟槽后的变幅杆频率少量偏移，通过调整变幅杆的结构尺寸，将谐振频率修正至35 kHz，图6为上述沟槽参数下变幅杆的模态分析结果。

螺旋沟槽式变幅杆的位移等值线如图6(a)所示，变幅杆振动较为均匀。通过模态分析的振型向量图6(b)可知，螺旋沟槽结构对变幅杆的振型进行了转换，与理论推导结果相吻合。

2.1 单个螺旋沟槽参数的影响

分别改变螺旋沟槽数目n、螺旋角度θ、槽宽d等参数，采用相同的ANSYS软件设置参数，逐一进行模态分析，提取纵-扭复合振动模态。螺旋沟槽结构参数的变化对变幅杆放大倍数m的影响如图7所示。

由图7(a)(b)可知，变幅杆放大倍数m随螺旋沟槽数目n、螺旋角度θ、槽宽d的变化产生轻微的波动，且其波动范围非常小。可认为螺旋沟槽结构参数的变化对变幅杆放大倍数m基本无影响。

图6 螺旋沟槽式变幅杆的模态分析结果Fig．6 Modal analysis results of horn with helical slots

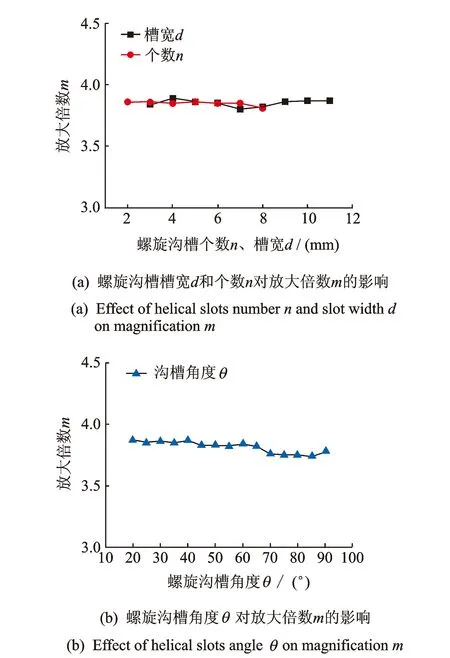
图7 螺旋沟槽参数对变幅杆放大倍数m的影响Fig．7 Effect of helical slots parameters on magnification m

模态分析中的位移不是绝对位移，但可利用相对位移来代替绝对位移，进行纵向振动分量与扭转振动分量的对比。定义螺旋沟槽变幅杆输出端面不在轴线上某一质点P的扭转振动位移Un与纵向振动位移Uz之比为扭纵分量比j，即

j=Un/Uz

(15)

螺旋沟槽结构参数的变化对扭纵分量比j的影响如图8所示。

图8 螺旋沟槽参数对扭纵分量比j的影响Fig．8 Effect of helical slots parameters on the torsional and longitudinal component ratio j

由图8(a)可知，螺旋沟槽槽宽d的大小对扭纵分量比j的影响较小，变幅杆输出端上的质点P的扭纵分量比j随槽宽d的改变略有增加；在沟槽数目为2～5个时，P点的扭纵分量比j随沟槽数目n的增加而显著增加，即扭转分量变大，当沟槽数目n继续增大，扭纵分量比增加趋缓。由图8(b)可知，质点P的扭纵分量比j随螺旋角度θ的增大而增大，并在35°时达到峰值，之后(当θ>35°时)，扭纵分量比随螺旋角度θ的增加逐步减小，直到θ=90°时j趋近于0。

综上所述，螺旋沟槽数目n、螺旋角度θ、槽宽d等参数的变化对变幅杆的输出“总量”无影响，只是改变了纵向振动分量与扭转振动的分量的比值。

2.2 多个螺旋沟槽参数的影响

采用如表1所示的三因素三水平正交参数进行模态分析，分析多个螺旋沟槽参数对变幅杆输出端某质点扭纵分量比的影响。通过极差R1的分析，影响纵扭分量的主次顺序为螺旋沟槽数目n>螺旋角度θ>槽宽d。

表1 正交螺旋沟槽参数与扭纵分量比的三因素三水平极差分析

3 实验分析

3.1 扭转测评方法

模态分析中定义的材料是均匀的，而实际加工所用的材料的大都均匀性不好，存在或多或少的缺陷，由此导致实际结果与仿真结果的偏差。为验证有限元分析的结果，现加工出螺旋角度为30,45和60°的螺旋沟槽变幅杆，每个角度分别开设2个和4个螺旋沟槽，沟槽的槽宽d=6 mm，槽深h=7.5 mm。

为精确测定质点P的扭振振幅，设计了一种扭转振动测评方法。如图9所示，对变幅杆进行加工，在小圆柱端面上沿其直径切除一个半圆形台，在变幅杆径向方向上形成一个平面，如图10所示，沿变幅杆径向方向将小圆柱段半径进行7等分，即划分8个测定点。测定点编号及其对应的与变幅杆轴线的距离如表2所示。借助型号为VW9000高速摄影仪及高精度激光位移传感器将激光束精确定位到每个测定点上，对每个测定点扭转振幅Un的测定。测定点的划分及扭转计算原理如图11所示，扭转振动测评现场如图12所示。

图9 加工后的变幅杆结构示意图Fig．9 The schematic diagram of the horn structure after processing

图10 变幅杆上的测定面结构Fig．10 Measurement surface structure on the horn

Tab.2Thedistancebetweenthemeasurepointandhornaxis

测定点12345678距变幅杆轴线距离/mm01234567

图11 测定点的划分及扭转计算原理Fig．11 The division of measurement points and the principle of torsion amplitude calculation

图12 扭转振动测评现场Fig．12 Torsional vibration measurement site

以测定点与变幅杆轴线的距离i作为横坐标，扭转振幅Un为纵坐标，利用测定数据绘制扭转振幅测定曲线，采用最小二乘法拟合出一条正比例函数y=1.35x，即建立该变幅杆的扭转幅度函数曲线，如图13所示。

图13 扭转幅度函数曲线Fig．13 Torsion amplitude function curve

图13中可看到，在8号测定点，扭转振幅Un急剧下降，与扭转幅度函数曲线有较大偏差。究其原因：8号测定点位于变幅杆半径的边缘处，变幅杆扭转振动时，激光有段时间没有集中在变幅杆上，传感器接收不到反射引号，造成扭转振幅Un测量的不准确。

变幅杆扭转振动角度正切值e

e=tan∠A=Un/i

(16)

其中：A为变幅杆的扭转振动角度。

扭转幅度函数曲线的斜率k为变幅杆扭转振动角A的正切值e，测量质点P到变幅杆轴线的距离i=6.4 mm。

质点P的扭转振幅可近似通过拟合的曲线进行计算

Un=iPe=iPK=6.4×1.35=8.64 μ m

(17)

3.2 实验与仿真结果的对比

纵向振动的输出在变幅杆输出端面是均匀的，故将激光束集中在端面上即可测量纵向振幅，其纵向振幅为Uz=11.8 μm。即质点P的扭纵分量比

j=Un/Uz=8.64/11.8=0.71

(18)

使用该方法对所加工的系列变幅杆相同位置的质点的扭纵分量比进行测定，实测结果与仿真结果的误差很小，实测质点P的扭纵分量的变化趋势与仿真结果的变化趋势基本一致，如图14所示。

图14 纵扭分量的实测结果与仿真结果的对比Fig．14 Comparison of measured results of longitudinal and torsional components with simulation results

4 结束语

笔者理论推导了螺旋沟槽结构的纵-扭模态的转换，分析了纵振振幅与扭转振幅对变幅杆输出端的椭圆振动轨迹的影响。基于有限元仿真探究了螺旋沟槽参数对变幅杆振动特性的影响，对部分结果设计实验加以验证，可以得到以下结论：a.螺旋沟槽数目n、螺旋角度θ、槽宽d的变化对变幅杆放大倍数m基本无影响;b.变幅杆输出扭纵分量比j随槽宽d的增加略有上升；随螺旋沟槽数目n的增加而变大；随螺旋角度θ的增加的先上升而后下降。影响纵扭分量的主次顺序为螺旋沟槽数目n>螺旋角度θ>槽宽d。

在纵振式变幅杆上开设螺旋沟槽，成功输出纵-扭复合振动。通过合理选择螺旋沟槽几何参数，实现对输出端的扭纵分量比j的控制，从而得到超精密加工所需的椭圆振动模式。