球形玻璃珠填充模腔的流动特性试验

(济南大学 机械工程学院，山东 济南 250022)

压片机是一种将粉末物质压制成型的通用设备，广泛应用于制药、粉末冶金、玻璃、陶瓷等工业生产领域。压片机的种类有很多，主要有单冲式压片机、 旋转式压片机和旋转式强迫喂料压片机。 压片机的压片工艺包括填充、压片和脱模3个步骤。压片机的结构以及压片工艺参数同时对压片质量产生重要影响。

压片机的重要性并未引起国内学者们的普遍关注，虞雅萍等[1]对压片机的压片过程进行了综述。国外的学者们对压片机的研究成果主要集中在压片机的压制阶段[2-4]和填充模腔阶段[5-9]，但只针对强迫喂料旋转压片机的有关结论不具有普遍适用性，只能为改进类似压片机的压片工艺提供一定的参考。

为了得到更普遍的粉体填充模腔的规律，揭示影响填充效率和质量的关键因素，以邬传宇教授为代表的学者们利用“送料靴-填充模腔直线填充系统”研究了粉体的填充过程，在粉末冶金和制药等领域开展了大量的研究工作，发现送料靴在带动制药辅料一起运动时，在惯性力作用下辅料会向后移动，辅料的头部会和送料靴的前壁形成一定的间隙，由于顶部间隙大，底部间隙小，形成近似鼻子的形状，由于辅料具有一定的黏性，这个“鼻子”的形状可以一直保持下来；当辅料头部运动到模腔上方时，如果填充速度较低，整个“鼻子”发生断裂掉入到模腔中，同时空气溢出，此种流动称为Nose流动；而当速度较高时，鼻子来不及断裂，无法全部进入模腔，送料靴底部的粉体在重力作用下按照某一层厚度流入模腔，此时模腔中的空气难以排出，此种流动称为Bulk流动。这些规律适合于具有粘性特性的材料，但是对玻璃珠不太适用。另外还发现送料靴速度是一个重要参数，一般来讲，送料速度越慢，得到的松装密度越大[10]。

Hjortsberg等[11]的研究却得到了相反的结论。Schneider等[12]利用模腔-送料靴试验模型研究了真空中粉体填充模腔的过程。Jackson等[13]又进一步证实了吸入式填充工艺的显著效果。Mills等[14]研究了颗粒大小和密度对粉体填充模腔行为的影响。Freeman等[15]研究了多种粉体特性对填充工艺的影响。为了研究粉末填充模腔的普遍规律，Wu等[16]、Sinka等[17]将压片机抽象为送料靴-模腔组合的试验系统，揭示药片辅料填充模腔的流动规律。

为了揭示玻璃珠填充模腔的运动机制，本文中利用一套送料靴-模腔自动填充试验系统研究玻璃珠填充模腔的流动行为。首先研究玻璃珠的特性，包括玻璃珠的形状、尺寸、球形度、玻璃珠之间的粘性、空气敏感指数等；然后，利用高速相机记录玻璃珠在送料靴中的运动行为以及在模腔中的填充流动过程；最后，利用邬传宇教授提出的临界速度概念[16]分析玻璃珠的填充效率和填充特点。通过揭示球形玻璃珠填充模腔的流动特性规律，为改进玻璃珠的填充工艺提供理论依据。

1 试验设计

1.1 试验材料

采用的玻璃珠为球形实芯玻璃珠。随机选取10个玻璃珠，利用游标卡尺测量其直径，平均值为1.99 mm；玻璃的密度为2 500 kg/m3；玻璃珠之间的粘结力为零。

玻璃珠填充模腔的过程是在空气环境中进行的，玻璃珠填充模腔的过程也就是玻璃珠置换模腔中空气的过程。空气溢出模腔时，空气流动是否对玻璃珠的流动行为产生影响以及影响的程度是一个需要研究的问题。

Guo等[18]利用一个无量纲方程给出了颗粒的空气敏感指数与材料密度和颗粒质量之间的关系，空气敏感指数的计算公式为

ζ=Arφρ

,

(1)

式中：Ar是颗粒在空气中流动的阿基米德常数，φρ是归一化粒子密度，其各自的计算公式为

(2)

(3)

式中：ρa是空气密度，取为1.205 kg/m3；ρs是颗粒的真实密度，试验中玻璃珠密度设为2 500 kg/m3；dp为玻璃珠直径，设为1.99 mm；η为空气黏度，其值为1.78e-5Pa·s，g为重力加速度，取为9.8 m/s2。

将式(2)、(3)代入式(1)中，利用MATLAB绘图得到玻璃珠的空气敏感指数随玻璃珠直径变化的曲线，如图1所示。纵坐标为玻璃珠的空气敏感指数，以指数形式表示，是一个无量纲量。Guo等[18]的研究表明，空气敏感指数ζ为9.6×106时是一个临界值，当某种颗粒的ζ值低于9.6×106时，该材料属于空气敏感材料，反之为空气惰性材料。

由图1可知，P1点代表1.99 mm玻璃珠的空气敏感指数，其数值为1.55×109，可以看出其位置远远高于下方的水平线，说明1.99 mm玻璃珠的空气敏感指数远远大于临界值9.6×106，1.99 mm玻璃珠为空气惰性材料。当其填充模腔时，空气对其流动行为的影响可以忽略。P2点为玻璃的空气敏感指数与9.6×106临界值之间的交点，该点的横坐标为0.37 mm，说明直径小于该数值的球形玻璃珠填充模腔时，其填充运动会受到空气的影响。

图1 玻璃珠直径对空气敏感指数的影响Fig.1 Air sensitivity index as a function of diameter of Glass Beads

1.2 试验系统

直线填充模腔试验系统如图2所示，由控制单元、 直线执行机构、 送料靴和模腔等部分组成。送料靴的运行速度范围为0～1 m/s，最大行程为0.6 m。 填充模腔固定于桌面的下方，当送料靴在静止桌面上划过时，玻璃珠会在重力的作用下填充模腔。 利用高速成像系统快速高清地记录玻璃珠在各种运动速度下自送料靴下落到填充模腔的全过程。

1—控制单元；2—直线执行机构；3—送料靴；4—模腔。图2 直线填充模腔试验系统 Fig.2 Linear die filling system

2 结果和讨论

2.1 Hopper流动

玻璃珠是球形的，并且玻璃珠之间粘结力为零，因此其流动性应明显好于制药工业中的辅料。当送料靴的送料速度较低时，鼻子的形状不容易保持，仿佛有一个相对于送料靴不断移动的漏斗，该漏斗区域始终处于模腔的上方，玻璃珠从漏斗区域下落填充模腔，该填充形态既不是Nose流动，也不是Bulk流动，而是另一种填充形态，本文中称之为Hopper流动，其示意图如图3所示。Hopper流动形态的存在，使得填充过程变得更为复杂，给压片质量的控制带来了更多的困难。

图3 Hopper流动示意图Fig.3 Illustration of Hopper flow

2.2 送料靴速度的影响

将玻璃珠倒入送料靴中，装满后继续倒入，直至出现一个尖堆，用刮板将尖堆刮平，从而保证每次试验时送料靴中的玻璃珠具有相同的初始状态。

将高速相机的采样频率设为10 000 Hz，分别记录200、400、1 000 mm/s这3种不同送料靴速度时的玻璃珠填充模腔过程，如图4、5、6所示。每种送料靴速度下拍摄了4张图片，分别表示填充过程中在开始、平稳、中间和结束这4种时刻的填充状态。

由图4可知，当送料靴的速度为200 mm/s时，玻璃珠下落到t=120 ms时模腔被填满，此时送料靴还在模腔上方，送料靴在模腔上方停留了足够长的时间。当t=0 ms时，送料靴中的玻璃珠因惯性所形成的的倾斜角并不大，玻璃珠与送料靴前壁未发生分离，玻璃珠前端的鼻子未能形成，无法发生Nose流动，所以玻璃珠以Hopper流动为主，整个流动过程较为平稳。

由图5可知，当送料靴的速度为400 mm/s时，玻璃珠下落到t=87.4 ms时填充结束，模腔右上角未被填满，此时送料靴刚刚通过模腔上方。当t=0 ms时，送料靴中的玻璃珠因惯性所形成的倾斜角逐渐变大，玻璃珠与送料靴前壁还存在一定的接触，所以玻璃珠仍旧以Hopper流动为主，整个流动过程较为平稳。

a t=0 msb t=40 msc t=80 msd t=120 ms图4 当送料靴速度为200 mm/s时玻璃珠填充模腔的过程Fig.4 Die filling process of glass beans at filling speed 200 mm/s

a t=0 msb t=27.4 msc t=47.4 msd t=87.4 ms图5 当送料靴速度为400 mm/s时玻璃珠填充模腔过程Fig.5 Die filling process of glass beans at filling speed 400 mm/s

由图6可知，当送料靴的速度为1 000 mm/s时，玻璃珠自下落到t=40.3 ms结束，模腔只填充了1/3左右，此时送料靴已通过模腔上方。说明送料靴速度越快，送料靴在模腔上方停留时间越短，模腔越难以填满。送料靴中的玻璃珠因惯性所形成的倾斜角接近90 °，而且向上鼓凸，玻璃珠与送料靴前壁完全分离，并且出现不小的间隙，鼻子形成，但是速度太快无法发生Nose流动，以Bulk流动为主。

a t=0 msb t=12 msc t=25.2 msd t=40.3 ms图6 当送料靴速度为1 000 mm/s时玻璃珠填充模腔过程Fig.6 Die filling process of glass beans at filling speed 1 000 mm/s

通过对比观察图4、 5、 6可知，送料靴速度为200、 400 mm/s时的玻璃珠流动较为平稳，以Hopper流动为主；而送料靴速度为1 000 mm/s时的玻璃珠因进入模腔中时与模腔壁发生较剧烈碰撞，运行不是很平稳，而且，因运行速度太快，没有充足时间形成Nose流动和Hopper流动，全程以Bulk流动为主。

2.3 玻璃珠临界填充速度

为了实现粉体填充模腔的定量分析，从而更好地指导生产实践，在送料靴-填充模腔的设计模型基础上，邬传宇教授进一步提出了临界填充速度的概念[16]。其将模腔的填充率设为

(4)

式中：mX为在某一送料靴速度下，填充到模腔中的粉体质量；M为模腔完全填满时的粉体质量，此处的粉体是松装状态，不能压实。

为了更精确地描述填充曲线，填充率与送料靴运动速度的关系表达式为

(5)

式中：vc为送料靴的临界运动速度；vs为送料靴的实际运动速度；n为指数，其值介于 1～1.6之间[10]。

为了实现玻璃珠填充模腔工艺过程的定量描述，分别考察了在6种送料靴运动速度下玻璃珠填充模腔的情况。为了保证试验结果的准确性和可重复性，每种速度重复3次，然后求平均值，玻璃珠填充模腔试验数据如表1所示。填充率随送料速度变化曲线如图7所示。纵坐标代表填充率，是一个不大于1的无量纲量。

表1 玻璃珠填充模腔试验数据

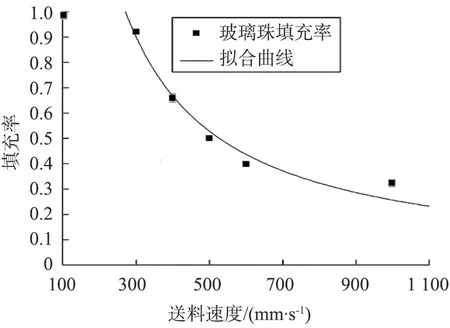
图7 填充率随送料速度变化曲线Fig.7 Die filling ratio as a function of die filling speed

由表1和图7可以看出，3次填充率的方差都很小，几乎可以忽略，说明玻璃珠的流动性很好，使得试验结果的重复性很高。黑色实芯方块代表6种送料靴速度的填充率，黑色曲线是根据公式(5)计算出的送料靴速度在300 ～1 000 mm/s范围内的5个点的拟合曲线，可以看出这5个点与曲线吻合的很好，填充规律十分明显。通过拟合，得到的填充率的曲线方程为

(6)

由式(6)可知，玻璃珠填充模腔的送料靴临界速度为270.7 mm/s，方程的指数n为1.040 8。送料靴采用该临界速度时，既能满足填充效果，又能实现最大的填充效率。

3 结论

1)空气对直径为1.99 mm的玻璃珠的流动运动行为不产生影响。当玻璃珠的粒径小于0.37 mm时，玻璃珠填充模腔的运动行为才会受到空气影响。

2) 填充速度为200 、400 mm/s时，玻璃珠以Hopper流动为主；填充速度为1 000 mm/s时，玻璃珠以Bulk流动为主。

3)直径为1.99 mm的玻璃珠填充时送料靴的临界速度为270.7 mm/s，方程的指数n为1.040 8。

上述结论为后续玻璃珠填充工艺的改进提供了理论依据，也为其他粉体压片机填充工艺的深入研究提供了参考案例。