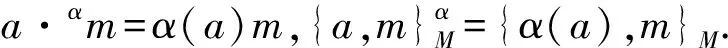多项式Poisson代数上的有限维单Poisson模
陈炜红, 吕家凤
(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
Poisson代数起源于哈密顿力学的研究,在Poisson几何和量子群中占有重要地位.由于Poisson代数在数学的很多领域都有重要的作用,近几十年来,有关Poisson代数有许多推广,如非交换的Poisson代数[1]、DG Poisson代数[2]、Poisson Hopf代数[3]等.而在Poisson代数中,Poisson模、单模又是它的一个重要研究内容.文献[4-8]对多项式环进行探究,得到多项式环上的有限维单Poisson模结构.本文采用文献[8]的思想方法,探究一类Poisson代数的有限维单Poisson模结构.
本文中,A是复数域C上的可交换的Poisson代数[6],M是A-模,J是A上的Poisson极大理想.
对于C-代数T,其生成元x,y,z与t±1满足下列关系:
xy-t-2yx=a(1-t-2)z;yz-t-2zy=b(1-t-2)x;zx-t-2xz=c(1-t-2)y.
且
xt=tx,yt=ty,zt=tz,tt-1=1=t-1t.
其中:a,b,c∈C{0};且t为T的中心元.
若t为非单位元、非零因子的中心元,则对于上述的T,A=T/[(t-1)T]为交换代数且同构于C[x,y,z].因此,A上具有一个自然的Poisson括号{-,-}:
{x,y}=2(az-yx); {y,z}=2(bx-zy); {z,x}=2(cy-xz).
(1)
本文主要研究A上的所有有限维单Poisson模结构.已知有限维单Poisson模的零化子为Poisson极大理想[7],首先回顾了一些基本概念,计算得出A的5个Poisson极大理想;然后分别根据Poisson极大理想J1和J2,探究有限维单Poisson模的构造;最后通过Poisson同构,将有限维单Poisson模的构造从J2转化到J3,J4,J5,得到了一类Poisson代数的有限维单Poisson模结构.
1 Poisson模和Poisson极大理想
首先回顾一些基本概念及相关结果,然后据此结果,得到A的Poisson极大理想.
定义1设J是Poisson代数A的理想.若对任意的j∈J,a∈A,有{j,a}∈J,则称J是A的Poisson理想;若Poisson理想J又是A的极大理想,则称J是A的Poisson极大理想.
定义2设(A,{-,-})是可交换的Poisson代数,M是A-模.若存在线性映射{-,-}M:A×M→M,对任意的a,b∈A,m∈M,满足:
1){a,bm}M={a,b}m+b{a,m}M,
2){ab,m}M=a{b,m}M+b{a,m}M,
3){{a,b},m}M={a,{b,m}M}M-{b,{a,m}M}M,
则称M为PoissonA-模.
定义3设J是Poisson代数A的一个理想,M是A-模,则J在M中的零化子可定义为:annMJ={m∈M:mj=0,j∈J}.
如果M是有限维单Poisson模,那么M的零化子是A的Poisson极大理想[8].因此,要探究Poisson代数A上的有限维单Poisson模,需先计算出A的Poisson极大理想.
引理1设(A,{-,-})是满足式(1)的Poisson代数,则A仅有5 个Poisson极大理想,且这5个Poisson极大理想如下所示:
证明 设J是A的Poisson极大理想,根据文献[9]中的引理1.4可得:对任意的m,n,l∈C,有J=(x-m,y-n,z-l).由于J是Poisson极大理想,所以{x,J}⊆J,{y,J}⊆J,{z,J}⊆J.考虑
2(az-yx)={x,y-n}∈J, 2(bx-zy)={y,z-l}∈J, -2(cy-zx)={x,z-l}∈J,
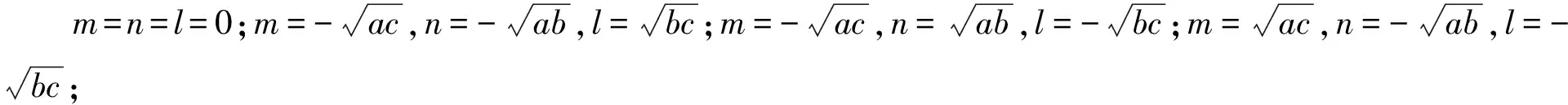
2 被J1零化的Poisson模
接下来讨论满足式(1)的多项式代数A=C[x,y,z]被J1零化的有限维单Poisson模结构.由定义3计算可得如下引理:
引理2设M是被J1零化的Poisson模,则对任意的m∈M,有
1)xm=ym=zm=0;
2){xy,m}M={yz,m}M={zx,m}M=0;
3){x,{y,m}M}M-{y,{x,m}M}M=2a{z,m}M,{y,{z,m}M}M-{z,{y,m}M}M=2b{x,m}M,
{z,{x,m}M}M-{x,{z,m}M}M=2c{y,m}M.
根据定义2,可将引理2转化为
引理3设M是被J1零化的Poisson模,对于λ∈C,0≠m∈M,满足{x,m}M=λm,则
1){x,{y,m}M}M=2a{z,m}M+λ{y,m}M;
2){x,{z,m}M}M=λ{z,m}M-2c{y,m}M;
3){y,{z,m}M}M-{z,{y,m}M}M=2bλm.
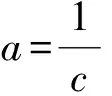
2.1 当a=c时,被J1零化的Poisson模
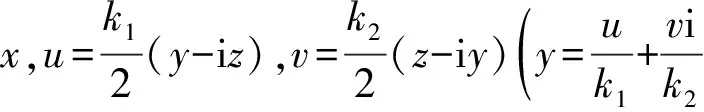

(2)
于是,有
引理4设M是被J1=xA+uA+vA零化的PoissonA-模,对任意的m∈M,可得:
1)xm=um=vm=0;
2){xu,m}M={xv,m}M={uv,m}M=0;
3){x,{u,m}M}M-{u,{x,m}M}M=2ci{u,m}M,{x,{v,m}M}M-{v,{x,m}M}M=-2ci{v,m}M,{u,{v,m}M}M-{v,{u,m}M}M=k1k2b{x,m}M.
引理5设M是被J1零化的PoissonA-模,对于0≠m∈M,存在λ∈C,满足{x,m}M=λm,则
1){x,{u,m}M}M=(λ+2ci){u,m}M;
2){x,{v,m}M}M=(λ-2ci){v,m}M;
3){u,{v,m}M}M-{v,{u,m}M}M=k1k2bλm.
引理 6对任意的整数d≥1,存在基为m1,m2,…,md的d-维PoissonA-模M,满足M被J1零化,并且
1)当1≤j≤d时,{x,mj}M=(λ+2(j-1)ci)mj;
2)当j=1时,{v,m1}M=0,当1 3)当j=d时,{u,md}M=0,当 1≤j 其中,λ=(1-d)ci. 证明 根据文献[8],需证明:当m=mj,{a,b}={x,u},{x,v},{u,v}时,定义2中的1)和3)成立.为了证明定义2中的3)成立,首先要证明,对任意的1≤j≤d, {{x,u},mj}M={x,{u,mj}M}M-{u,{x,mj}M}M. 当1≤j 且 {x,{u,mj}M}M-{u,{x,mj}M}M={x,mj+1}M-{u,(λ+2(j-1)ci)mj}M= (λ+2jci)mj+1-(λ+2(j-1)ci)mj+1=2cimj+1. 当j=d时,{{x,u},md}M=2ci{u,md}M=0,且 {x,{u,md}M}M-{u,{x,md}M}M=0-(λ+2(d-1)ci){u,md}M=0. 同理可证得:对任意的1≤j≤d, {{x,v},mj}M={x,{v,mj}M}M-{v,{x,mj}M}M; {{u,v},mj}M={u,{v,mj}M}M-{v,{u,mj}M}M. 当然,仍需证明当m=mj,{a,b}={x,u},{x,v},{u,v}时,定义2中的1)成立.首先,由引理4中的1)可得 {x,umj}M={x,vmj}M={u,vmj}M=0. 其次,由式(2)得 所以,定义2中的1)成立.引理6证毕. 引理7对于任意的整数d≥1,M满足引理6,则A的d-维Poisson模M是单Poisson模. 此时,非零系数的个数比n少1.由n的最少性可得:当j≠k时,{x,n}M-λkn=0,即αj=0.故n=αkmk,mk∈N.则N=M,M是一个单Poisson模.引理7证毕. 引理8设M是被J1零化的有限维单PoissonA-模,n≤dimM,则存在λ∈C和n个线性无关的元m1,m2,…,mn∈M,满足 1)当1≤j≤n时,{x,mj}M=(λ+2(j-1)ci)mj; 2)当j=1时,{v,m1}M=0,当1 3)当1≤j 证明 数学归纳法.当n=1时,设θ={λ∈C|对于一些0≠m∈M,{x,m}M=λm}.因为M是有限维模,所以对任意的m∈M,都存在一个特征值,满足M的线性自同构:m|→{x,m}M.因此θ≠Ø.取λ∈θ,则存在0≠m1∈M满足{x,m1}=λm1.m1显然满足条件 1)~3). 假设上述结论对dimM≥n成立,现讨论dimM≥n+1 的情况.由归纳假设可知,M中存在线性无关的元m1,m2,…,mn和一些λ∈C,满足条件 1)~3).设mn+1={u,mn}M,则mn+1={u,mn}M≠0.否则,由m1,m2,…,mn生成的n维子空间就会变成M的Poisson子模,与dimM≥n+1时M是单的矛盾.下面证明mn+1满足条件1)~3).因为{x,mn}M=(λ+2(n-1)ci)mn,所以根据引理5中的1)可知 {x,mn+1}M={x,{u,mn}M}M=(λ+2nci)mn+1, 则当dimM≥n+1时,条件1)成立.又由引理4中的3)得 {u,{v,m}M}M-{v,{u,m}M}M=k1k2b{x,m}M. 当m=mn时,有 -k1k2b(n-1)(λ+(n-2)ci){u,mn-1}M-{v,mn+1}M=k1k2b{x,mn}M, 所以 {v,mn+1}M=-k1k2bn(λ+(n-1)ci)mn. 因此,当dimM≥n+1时,条件2)和3)成立.所以,m1,m2,…,mn+1为{x,-}M中的不同特征值对应的特征向量.因此,m1,m2,…,mn+1线性无关,结论成立.引理 8 证毕. 定理1设M是被J1零化的d-维单PoissonA-模,则M有一组基m1,m2,…,md满足: 1)当1≤j≤d时,{x,mj}M=(λ+2(j-1)ci)mj; 2)当j=1时,{v,m1}M=0,当1 3)当j=d时,{u,md}M=0,当1≤j 其中,λ=(1-d)ci. 证明 根据引理8,存在λ∈C和一组基m1,m2,…,md,使M满足条件1)~3),除{u,md}=0外.由引理5中的1)可得 {x,{u,md}M}M=(λ+2dci){u,md}M. 因为M是由特征值λ+2(j-1)ci(1≤j≤d)对应的特征向量mj生成的,所以λ+2dci不是{x,-}M的特征值,从而{u,md}M=0.由引理4中的3)可得 {u,{v,m}M}M-{v,{u,m}M}M=k1k2b{x,m}M, 则 -k1k2b(d-1)(λ+(d-2)ci)md=k1k2b(λ+2(d-1)ci)md. 得到d(λ+(d-1)ci)=0,所以λ=(1-d)ci.定理 1 证毕. 定理2对任意的整数d≥1,Poisson代数A存在唯一一个被J1零化的d-维单Poisson模,并且该模有一组基m1,m2,…,md满足: 1)当1≤j≤d时,{x,mj}M=(λ+2(j-1)ci)mj; {y,md}M=-k1bi(d-1)(λ+(d-2)ci)md-1; {z,md}M=-k1b(d-1)(λ+(d-2)ci)md-1. 其中,λ=(1-d)ci. (3) 按照a=c的情况,同理可得有限维单Poisson模的结构,结论如下: 定理3对任意的整数d≥1,Poisson代数A存在唯一一个被J1零化的d-维单Poisson模,并且该模有一组基m1,m2,…,md满足: 1)当1≤j≤d时,{x,mj}M=(λ+2(j-1)i)mj; {y,md}M=-k1bi(d-1)(λ+(d-2)i)md-1; {z,md}M=-k1bc(d-1)(λ+(d-2)i)md-1. 其中,λ=(1-d)i. 引理9设M是被J2零化的Poisson模,m∈M,则 (4) 根据定义2,可得到以下引理: 引理10设M是被J2零化的Poisson模,对于0≠m∈M,存在λ∈C,满足{s,m}M=λm,则 按照第2部分的证明方法,同理可得被J2零化的有限维单Poisson模结构,结论如下: 定理4对任意的整数d≥1,Poisson代数A存在唯一一个被J2零化的d-维单Poisson模,并且该模有一组基m1,m2,…,md,满足: 2)当1≤j α(x)=x,α(y)=-y,α(z)=-z. 由上可知,α(J2)=J3且α2为恒等映射.若M是被J2零化的单Poisson模,则被J3零化的单Poisson模为Poisson模Mα.此外,可得:对任意的整数d≥1,存在一个被J3零化的d-维单Poisson模.同理,对于被J4,J5零化的Poisson模,可定义C-自同构β和γ如下: β(x)=-x,β(y)=y,β(z)=-z; γ(x)=-x,γ(y)=-y,γ(z)=z. 因此,被J4,J5零化的d-维单Poisson模分别为Mβ,Mγ. 定理5对任意的整数d≥1,满足式(1)的Poisson代数A有5个d-维单Poisson模. 证明 由引理1、 定理2、定理3、定理4及 Poisson自同构可证.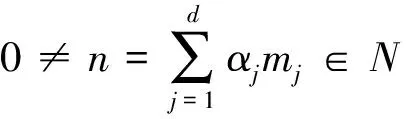
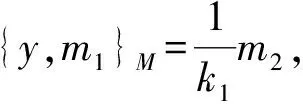

2.2 当时,被J1零化的Poisson模
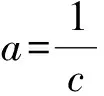
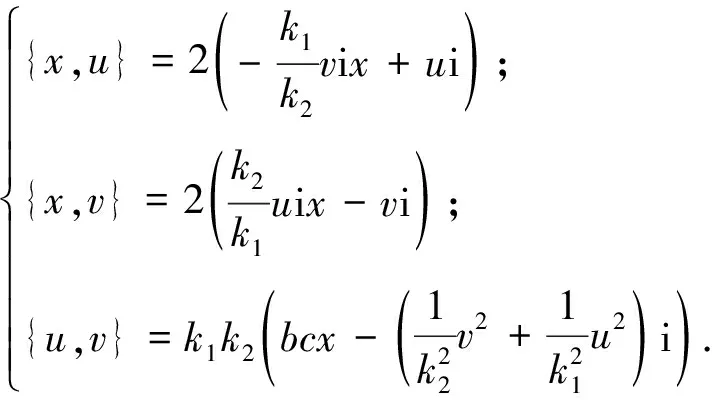
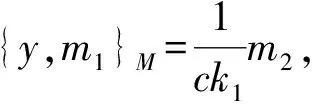

3 被J2零化的Poisson模
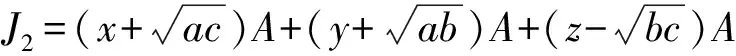
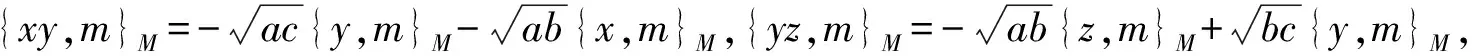
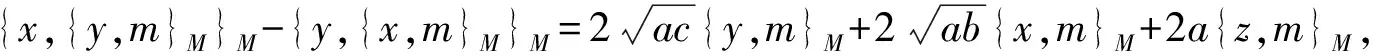
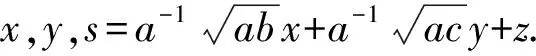
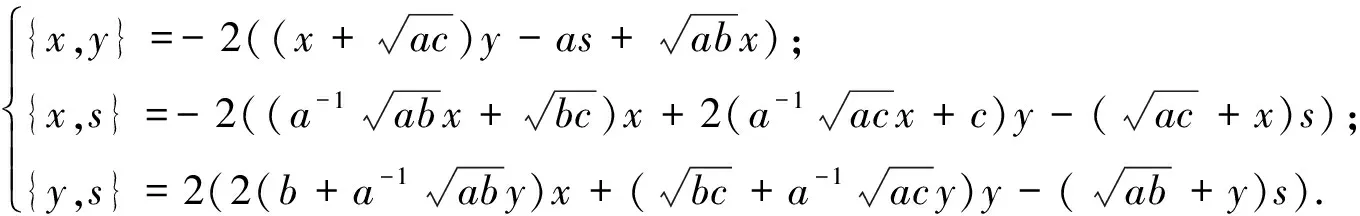

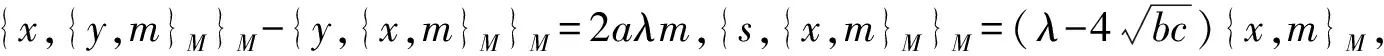
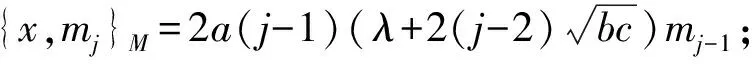
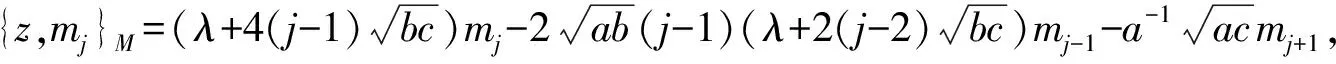
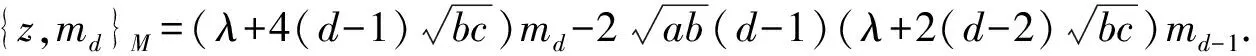
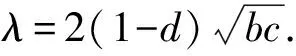
4 Poisson同构