基于改进樽海鞘群算法的四旋翼飞行器姿态优化控制

丁 力 高振奇 虞 青

(江苏理工学院机械工程学院， 常州 213001)

0 引言

四旋翼飞行器在民用领域有着广泛的用途，如农田喷雾、城市建模、地理测绘等。但因其强耦合、高非线性、欠驱动等特点也给高精度鲁棒控制器的设计带来了巨大的难度[1]。目前，已有很多先进的控制策略用来设计四旋翼的控制器，如自抗扰控制[2]、自适应控制[3]、模型预测控制[4]、反步法控制[5]等。然而，上述方法是需要精确的模型或者依赖大量的控制器参数，这极大地限制了其在实际工程中的应用。另外，由外界扰动、未建模动态、参数漂移等组成的集总干扰也会进一步加大上述控制器设计的难度。

在控制器设计过程中引入扰动观测器是解决上述问题一种有效途径。扰动观测器可估计集总干扰，提高系统的稳定性与控制性能。例如，文献[6]将反步法与非线性扰动观测器相结合，有效减弱了集总干扰对四旋翼控制性能的影响；为改善四旋翼容错控制效果，文献[7]采用高阶非线性扰动观测器去捕捉不确定项的动态特性。通常，非线性扰动观测器存在待整定参数多、控制耗能大、易触发执行器饱和等缺点。文献[8]提出的线性自抗扰控制(Linear active disturbance rejection control, LADRC)结构中的线性扩张状态观测器(Linear extended state observer, LESO)具有结构简单、耗能小的特点，可有效弥补非线性扰动观测器的不足。但LADRC中的比例微分(Proportion differentiation, PD)控制结构过分依赖跟踪误差信号、对闭环系统的动态变化极其敏感。鉴于上述分析，可尝试用另一种控制结构来替代PD，增强控制策略的控制性能。

滑模控制是一种能有效处理不确定问题的鲁棒控制技术，但它在处理四旋翼飞行器控制时也会带来一些问题，如大超调、长起调时间与强抖振等。为解决这些问题，文献[9]采用积分滑模控制器来抑制四旋翼控制中的抖振问题；文献[10]利用自适应策略来改进滑模控制，设计了四旋翼的轨迹跟踪控制器，并在仿真环境下获得了很好的抗干扰控制效果。近年来研究发现快速连续非奇异终端滑模控制(Fast-continuous nonsingular terminal sliding mode control, FNTSMC)既能有效改善传统滑模控制的不足，又能保证系统状态有限时间收敛。文献[11-13]分析了FNTSMC及其改进策略在工程控制中的能力。目前，同时考虑LESO与FNTSMC优势的四旋翼飞行器姿态控制的文献鲜有报道。

另外，参数整定是获得控制器最佳性能的一种有效方法，通常包括经验法与智能法两种形式。前者是通过人为试凑的方式来调整控制器参数，准确性低、工作量大、成功率低；后者是采用人工智能算法优化控制器参数，准确性高、通用性强、成功率高。因此，在学术研究中通常会选择后者。在人工智能算法中，樽海鞘群算法(Salp swarm algorithm, SSA)是由MIRJALILI团队于2017年提出的一种模拟樽海鞘群的协同运动与觅食行为的元启发式人工智能算法[14]。与传统的遗传算法、粒子群算法、萤火虫算法相比，SSA算法具有鲁棒性高、收敛速度快、参数设置少、结构简单等特点。但在优化具有多个局部极值的目标函数时，普通SSA算法也存在易陷入局部最优和进化停滞的缺陷。因此，研究一种改进的SSA算法来整定控制器参数意义重大。

本文结合LESO与FNTSMC的优势，提出一种基于线性扩张状态观测器的快速连续非奇异终端滑模控制策略(Fast-continuous nonsingular terminal sliding mode control based on linear extended state observer, FNTSMC-LESO)设计四旋翼的姿态控制器；引入樽海鞘群算法来解决控制器的参数整定问题，并引入一维正态云模型和自适应算子加强算法优化能力；通过仿真与试验对本文方法的有效性、实用性进行验证。

1 动力学建模

本文研究的对象为X450型四旋翼飞行器，如图1所示。描述其飞行动力学行为需要两套坐标系，即地球坐标系OEXEYEZE和机体坐标系OBXBYBZB。该飞行系统具有4个旋翼，每个旋翼产生运动所需的升力fmi与力矩Ti(i=1,2,3,4)。利用牛顿-欧拉方程可推导出四旋翼的姿态动力学模型[15]

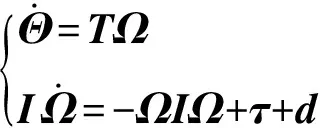
(1)

其中

Θ=(φ,θ,ψ)T
Ω=(p,q,r)T
τ=(τ1,τ2,τ3)T
d=(d1,d2,d3)T
I=diag(Ixx,Iyy,Izz)

(2)

式中Θ——地球坐标系中描述的欧拉角

φ——横滚角θ——俯仰角

ψ——偏航角

Ω——机体坐标系中描述的角速度

τ——输入力矩

d——外界扰动

I——转动惯量，取Ixx=Iyy=0.094 kg·m2，Izz=0.086 kg·m2

T——地球坐标系与机体坐标系之间的转换矩阵

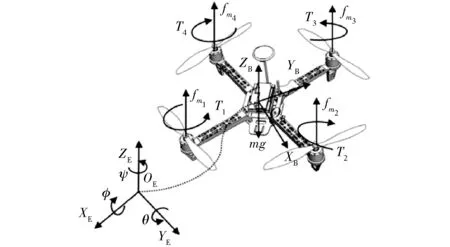
图1 四旋翼结构示意图Fig.1 Configuration of quadrotor

四旋翼的总升力τf与其他3个控制输入τ可通过4个桨叶的电机转速计算获得，即

(3)

其中

kf=ρCTAR2kτ=CMρAR2/kf

式中CT——升力系数

CM——反扭矩系数

ρ——空气密度，取1.29 kg/m3

A——旋翼桨盘面积，取0.08 m2

R——旋翼半径，取0.16 m

l——旋翼中心到四旋翼机体质心的距离，取0.2 m

ω1、ω2、ω3、ω4——电机转速

通过参数辨识试验[16]可拟合出kf与kτ的近似值为：kf≈2.5×10-5，kτ≈1.2×10-6。

2 姿态控制器设计

2.1 线性扩张状态观测器的设计

根据式(1)，姿态角每个通道的输出量与输入力矩项均呈现二阶导数关系，故可以将姿态动力学模型看成是3个二阶子系统来设计控制器。不失一般性，这里以一类常见的二阶系统来演绎FNTSMC-LESO控制器的设计过程。选用的二阶系统形式为

(4)

式中x1、x2——状态变量

u——控制输入y——系统输出

b——控制器增益

f(x1,x2,d(t),t)——包含了建模不确定性与外界扰动d(t)的集总干扰

将式(4)改写成状态空间方程形式

(5)

x=(x1,x2)Tu=u

y=yf=f

式中x——状态变量u——控制输入

y——系统输出f——集总干扰

A、B、C、E——系统矩阵

假设集总干扰是有界、可微分的，则可用一个扩张状态量来增广式(5)的形式，即

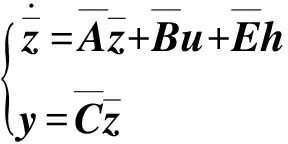
(6)

其中

式中x3——扩张状态量

设计式(6)的线性扩张状态观测器为

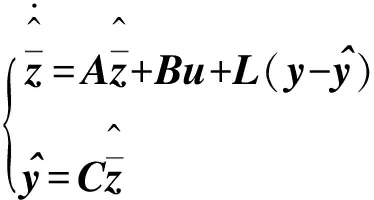
(7)

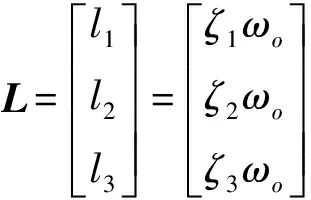
(8)

L——观测矩阵，可通过极点配置的方式计算[8]

ωo——观测器带宽，其值大于0

ζ1、ζ2、ζ3——特征根

特征根满足

(9)

2.2 快速非奇异终端滑模控制律的设计

定义连续快速非奇异终端滑模面函数为

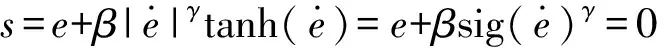
(10)

其中

式中e——跟踪误差

xr——参考信号

β、γ——控制器参数

这里用tanh连续函数替代滑模控制中常见的sign分段函数可有效削弱控制输入中的抖振现象。

将式(10)的一阶导数代入式(4)，可得到系统的等效控制输入为

(11)

进一步地，选取快速终端滑模趋近律来加快控制律的收敛速度，使得系统状态能在有限时间内收敛

(12)

式中k1、k2——控制器参数

进而，基于趋近律的控制输入ur为

ur=b-1(k1s+k2sig(s)p)

(13)

因此，FNTSMC-LESO控制器的控制输入可设计为

u=ue+ur

(14)

本文所设计的FNTSMC-LESO控制器结构如图2所示。在四旋翼姿态控制中，需要为3个姿态通道分别设计1个此类控制器。

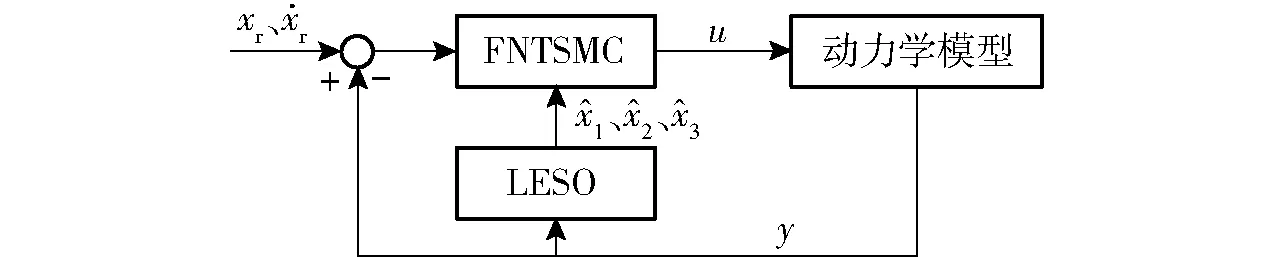
图2 FNTSMC-LESO控制结构图Fig.2 Structure of FNTSMC-LESO controller

3 稳定性分析

定理：对于式(4)描述的一类常见的二阶系统，若集总干扰是有界且可导的，在本文所设计FNTSMC-LESO控制律作用下，可保证跟踪误差及其一阶导数在有限时间内收敛到某个区域[17]，即

|e|≤2Δ=2min(Δ1,Δ2)

(15)

(16)

其中

Δ1=|3-f|/k1Δ2=(|3-f|/k2)1/p

证明：考虑一个Lyapunov函数为

(17)

它关于时间的一阶导数为

(18)

联立式(10)～(14)，可以推导出连续快速非奇异终端滑模面的一阶导数为

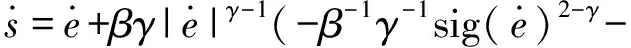
(19)

则有

(20)

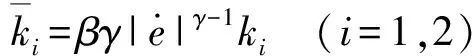
进而，式(18)也可被描述成其他两种形式

(21)

(22)

引理：如果Lyapunov函数V满足不等式

(23)

在此条件下的稳定时间为

(24)

式中V0——V的初始值

结合定理与引理，在假设成立的情况下，滑模面式(10)是有限时间稳定的，且可在有限时间内收敛到某个区域

(25)

(26)

整理式(25)、(26)，得

‖s‖≤Δ=min(Δ1,Δ2)

(27)

进一步地，为证明跟踪误差及其一阶导数的收敛性，将滑模面式(10)改写成

(28)

当‖s‖≤Δ时，跟踪误差的一阶导数可在有限时间内收敛，即

(29)

结合式(28)、(29)，得

(30)

跟踪误差在有限时间内收敛。

证明完毕。

4 参数整定

4.1 普通的SSA算法

在本文设计的FNTSMC-LESO中，将对控制器性能影响较小的参数作为先决条件，即设置γ=1.5和p=0.5。另外，每个FNTSMC-LESO中有4个参数需要整定，即：ωo、β、k1和k2，整个姿态控制器有12个参数待整定。在SSA算法中，将樽海鞘个体分为引领者与跟随者两种。引领者带领跟随者组成樽海鞘链游向最优的食物源，即最优或次优的控制器参数。算法具体步骤如下：

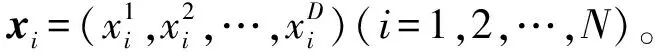
(2)计算适应度值。定义樽海鞘链追逐的食物源所获得适应度值为Fj(j=1,2,…,D)，在本优化问题中，Fj用误差平方乘以时间(Integral of time multiplied by the squared error，ITSE)这一性能指标来描述

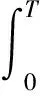
(31)

式中e(t)——时域内的跟踪误差

选择合适的有限时间T可使目标函数，也就是适应度值趋于一个稳定值。通过式(31)可获得初始的全局最优适应度值。

(3)更新引领者位置。引领者根据式(32)、(33)来获得当前位置。

(32)

c3=2e-(4Q/Qmax)2

(33)

buj、blj——个体在j维位置上的上、下限

c1、c2——0～1之间的随机数

c3——搜索平衡因子，用来权衡局部搜索和全局搜索的能力

Q——当前迭代次数

(4)更新跟随者位置。跟随者根据牛顿运动方程来更新位置

(34)

(35)

这样，樽海鞘链的觅食机制则可通过式(32)、(35)模拟。比较当前迭代中的适应度值与全局最优适应度值，将较好的个体保留到下一代中。

(5)记录下当前最优解。然后返回至步骤(3)循环迭代，直到Q=Qmax。

在普通SSA算法寻优过程中，全局搜索与局部搜索是个相互矛盾的过程，若此过程失衡，则算法极易陷入局部最优而导致收敛停滞。因此，本文引入一维正态云模型与自适应算子来改进引领者与跟随者的位置更新策略，得到一种改进的樽海鞘群算法(ISSA)。

4.2 改进算子

(36)

式中Ex——期望，表示定性概念模糊度的度量

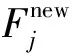
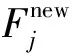
当迭代次数达到一定数量后，搜索到的适应度值会越接近最优值。为提高求解精度，控制搜索范围，采用非线性递减控制策略来调整xj的值

(37)

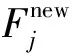
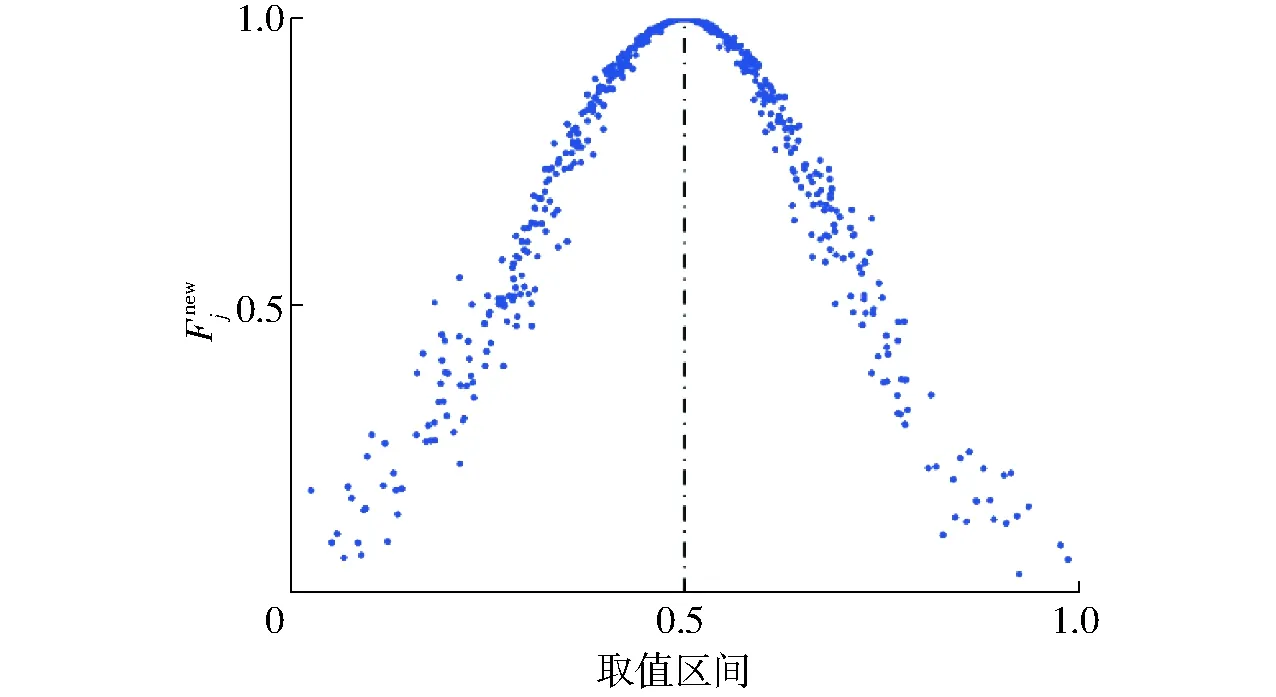
图3 500个邻域值的一维正态云模型Fig.3 1-dimension positive cloud model with 500 neighborhood values

在跟随者位置更新过程中采用自适应算子[19]来帮助SSA算法跳出局部最优的束缚，使樽海鞘个体在前期有较强的全局收敛能力，在后期能够得到相对准确的结果。自适应算子具体形式为

(38)

(39)

式中wmax、wmin——权重因子w的上、下限

rand()——0～1之间的随机数函数

若w的值过大，则算法搜索效率低，局部挖掘能力不足，不易得到最优解；反之，若w的值过小，算法的收敛精度较高，但全局搜索能力较弱，算法易陷入局部最优。而式(39)可有效解决上述问题。

5 结果分析

5.1 仿真1

采用一个阶跃信号来测试ISSA算法对FNTSMC-LESO控制器的参数整定能力。参考信号为Θr=(1.047,-1.047,1.571)Trad，欧拉角及其角速度的初始值均为0，系统中的集总干扰用随机噪声来模拟，仿真时间为10 s。为了更好地说明ISSA算法的性能，引入文献[20]提出的ABC算法及普通的SSA算法与ISSA算法做对比分析。3种算法的参数设置如表1所示。各算法重复仿真5次，然后选取其中最好的结果，如图4所示。从图4中可以看出，ISSA算法的收敛速度要快于其他两种算法，其获得最优解(0.002 4)的精度分别比SSA算法(0.017 3)和ABC算法(0.020 3)高出86.13%和88.18%。另外也可看出，SSA算法及其改进算法比ABC算法具有更强的数据挖掘能力。图5给出了基于ISSA算法的FNTSMC-LESO控制器参数整定过程。

表1 3种算法的参数Tab.1 Parameters of three algorithms

图4 3种算法的迭代曲线Fig.4 Iteration curves of three algorithms

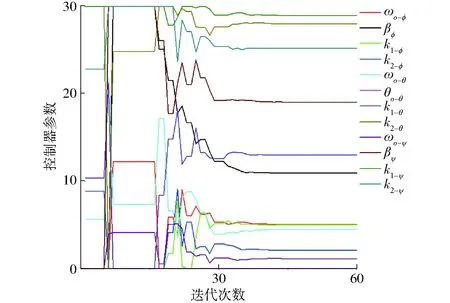
图5 ISSA算法整定后的参数Fig.5 Control parameters optimized by ISSA

图6给出了在FNTSMC-LESO控制下四旋翼飞行器姿态角的响应结果。在ISSA算法的优化下，本文所提控制器能获得令人满意的控制性能。仿真1的另一个作用是为其他仿真或试验提供一组合适的控制器参数。

图6 仿真1中姿态角的响应Fig.6 Response of attitude angles in simulation case 1

5.2 仿真2

本文设计FNTSMC-LESO控制器的想法来源于LADRC控制结构。不同点是FNTSMC-LESO引入FNTSMC来改进LADRC中PD控制律没有充分利用误差信号的缺陷。本算例以横滚角为例，让其去跟踪一个给定参考信号，以此来比较本文所提控制算法与LADRC的性能优劣。LADRC的控制器参数也通过ISSA算法整定。仿真结果如图7所示，可以看出FNTSMC-LESO在跟踪精度、响应速度及抗干扰能力上均优于LADRC。

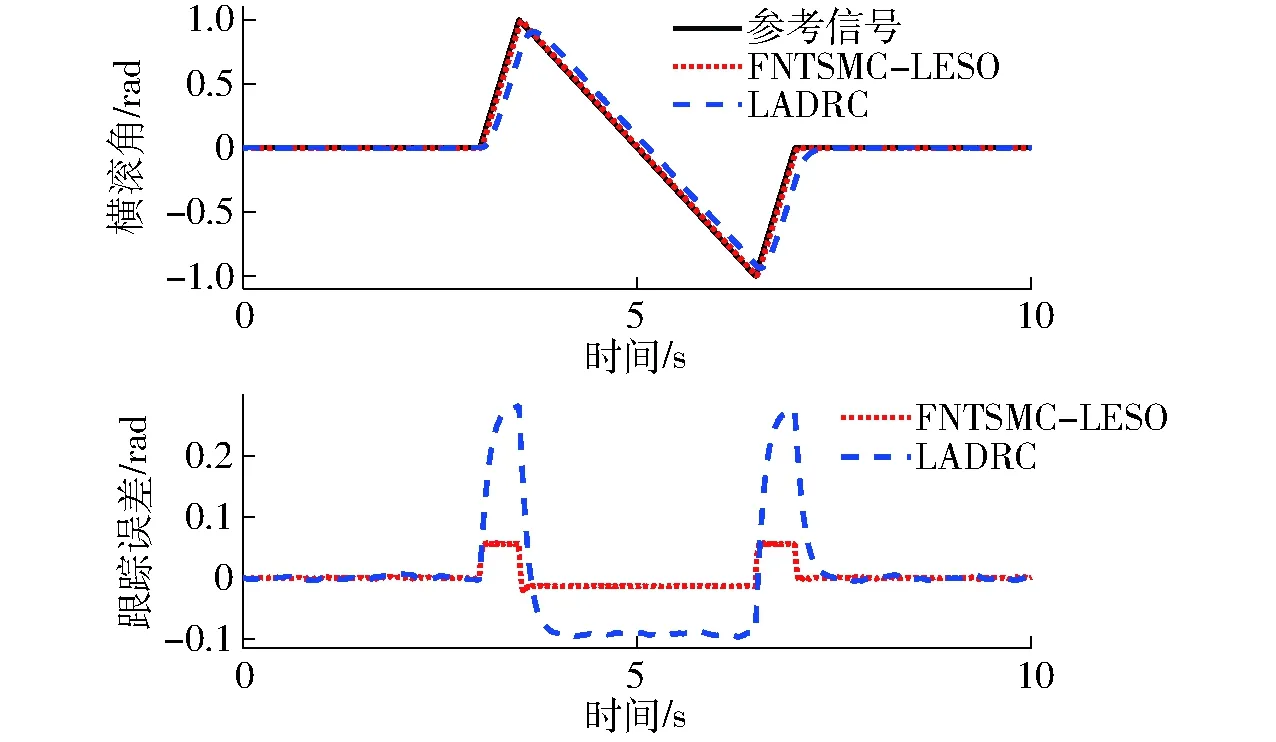
图7 仿真2中横滚角的响应Fig.7 Response of roll angle in simulation case 2

5.3 试验1

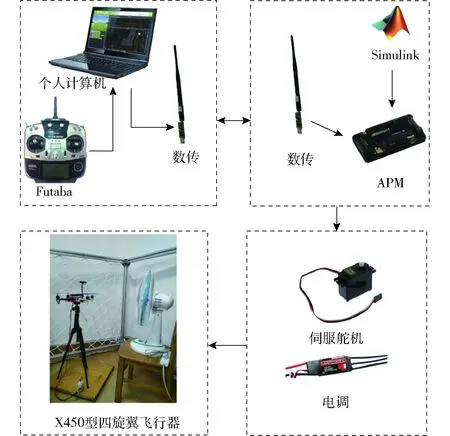
图8 X450型四旋翼飞行器试验平台Fig.8 X450 quadrotor experimental platform

为验证本文所提算法的实用性，搭建如图8所示的四旋翼飞行器试验平台。该平台由地面站、Futaba遥控器、APM开源飞控、一对数传、X450型四旋翼飞行器、变姿态机构等组成。姿态角信号通过飞控中集成的惯性测量单元(Inertial measurement unit, IMU)获取，并由数传实时传送至地面站个人计算机上，采样频率为50 Hz。另外，需要说明的是GPS模块在本试验中不起作用，但为了方便今后研究位置跟踪器的设计，故没有拆除。

试验前，将仿真获得的FNTSMC-LESO控制器参数通过APM2/Simulink的协议[21]烧录到APM飞控中。另外X450型四旋翼飞行器的安装角为-70°，以防止飞行器在不受控时因运动惯性而撞击变姿态机构的立柱。试验中，X450型四旋翼飞行器先由飞控手通过Futaba遥控器操控至悬停状态，然后切换到自由飞行模式去跟踪3种参考轨迹。试验中的外界扰动由一台可调速的电风扇提供。截取试验过程中的10 s数据用来分析，如图9所示。随着风速的增加，FNTSMC-LESO控制器的抗干扰能力也逐渐变弱，跟踪误差也随之变大。导致这种结果的原因可能有：控制器的参数是由仿真获得的，而非“量身定做”，故存在一定的偏差；试验中集总干扰的边界值是人为设定的值，无法做到像仿真那样可以对实际扰动值进行精确估计；试验中的机械振动、测量误差等因素会进一步放大跟踪误差。但总体来讲，本文所设计的控制器还是能够帮助X450型四旋翼飞行器有效跟踪上参考轨迹，这表明该控制策略有一定的实用性。

图9 试验1中姿态角的响应Fig.9 Response of attitude angles in experiment 1

5.4 试验2

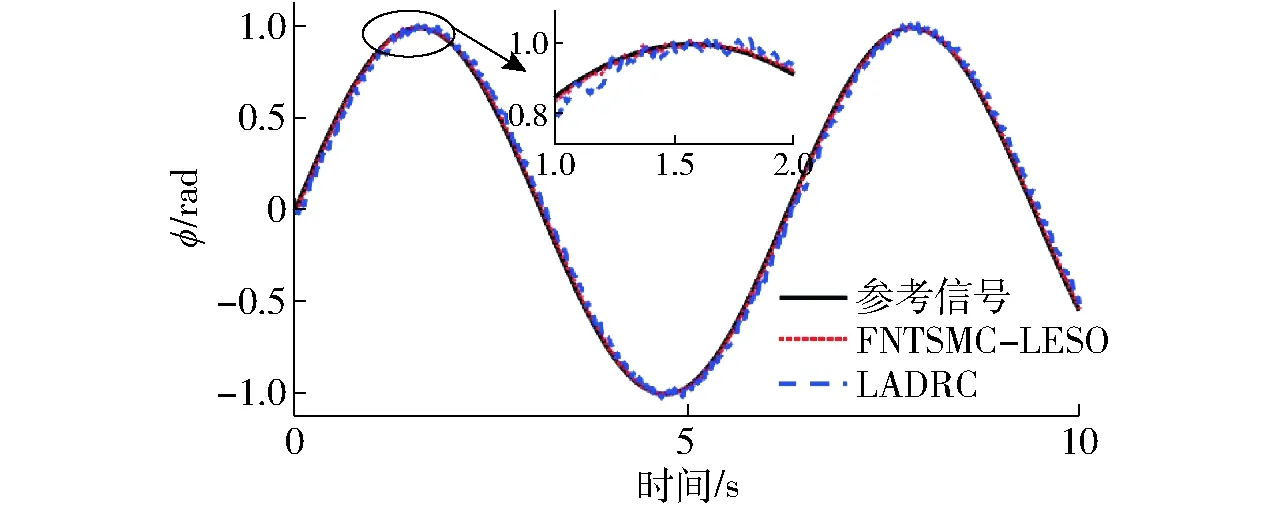
图10 试验2中横滚角的响应Fig.10 Response of roll angle in experiment 2

进一步地，将LADRC也烧录到APM开源飞控中，用来与本文方法比较在实际中应用的优劣。这里需要指出的是FNTSMC-LESO控制过程会涉及信号的一阶导数与二阶导数，若参考信号是非光滑曲线，则需引入微分器来求导，而微分器是物理不可实现的。因此，本试验以横滚角为例去跟踪一个给定正弦信号(风速设定为2.75 m/s)，结果如图10和图11所示。图10显示了两种控制器均能有效抑制集总干扰影响，而本文方法的跟踪精度要明显优于LADRC。图11表明与LADRC相比，本文方法可获得幅值更小的控制律，有效减弱了抖振，减小了控制信号对电机的冲击。

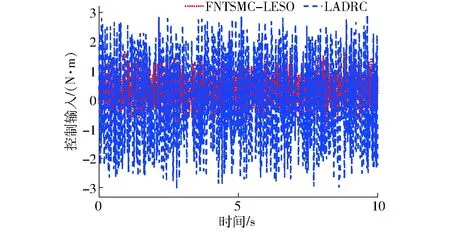
图11 两种控制器生成的输入信号Fig.11 Control inputs calculated by two controllers

随后，用最大误差(Maximum error, ME)与均方根误差(Root mean square error, RMSE)来评价两种控制器的跟踪精度。FNTSMC-LESO的ME值(0.018 5)比LADRC的ME值(0.087 6)小78.88%；同样地，前者的RMSE值(0.005 7)比后者的RMSE值(0.039 1)小85.42%。进一步说明了本文方法具有更高的控制精度。

6 结束语

提出了一种基于线性扩张状态观测器的快速连续非奇异终端滑模控制策略来解决集总干扰下四旋翼的姿态鲁棒控制问题。该控制器利用LESO来减弱集总干扰的影响，引入FNTSMC来加快控制律的收敛速度，使系统的跟踪误差能在有限时间内收敛到特定区域。与LADRC相比，本文方法不管在仿真或试验中都具有较高的控制精度、较强的抗干扰能力及较快的响应速度，也能有效削弱控制抖振，减小对电机的控制冲击。另外，也提出基于改进樽海鞘群算法优化的控制器参数整定方法。该算法用一维正态云模型和自适应算子来增强其数据挖掘能力，避免陷入局部最优。仿真结果表明，ISSA算法能够有效解决四旋翼姿态控制器的参数整定问题。