C/SiC复合材料螺钉拉伸强度分布模型

袁建宇 逄锦程 王 影 谢国君 卢克非

（航天材料及工艺研究所，北京 100076）

0 引言

C/SiC复合材料即使在高温下，也能保证较高的比强度、良好的断裂韧性以及优异的抗疲劳和蠕变能力，因此成为高超声速飞行器上应用的主要热结构材料[1-3]。由于航天飞行器形状复杂，一般采用多块复合材料拼接的方式进行飞行器热结构的制备，需要采用相容性好、热结构强度高的C/SiC复合材料螺钉来对热结构材料进行固定和连接，但该材料具有结构非均质性，因此其力学性能具有方向各向异性、尺度不均匀性以及几何与材料非线性等特点[4]。此外，在材料内部还存在基体裂纹、纤维脱粘和断开、层间开裂等各种缺陷和损伤[5]，且这些损伤通常是随机分布的，因此C/SiC复合材料的强度也存在着分散性。C/SiC复合材料的裂纹从萌生到扩展受控于多种因素，其中，材料的原始缺陷的影响不可忽略、复杂的制备工艺更加剧了材料在不同尺度上性能分散性，因此概率统计意义上的表征具备了合理性。基于此，研究者给出了大量的基于概率统计的复合材料强度理论模型，并以此为基础，推算和预测复合材料的强度，保证结构安全可靠。LARACURZIO[6]针对纤维增强陶瓷基复合材料提出了一个考虑温度作用的时间-损伤模型，并以CG-NicalonTM/SiC复合材料为例检验了模型的可靠性。杨程鹏等人[7]基于纤维损伤机理，建立了一个细观力学分析模型，对C/SiC复合材料无应力氧化残余强度进行模拟计算，分析了纤维氧化缺口对纤维断裂概率的影响。NADARAJAH等人[8]针对脆性和塑性基体的复合材料分别总结了20余种强度分布模型，并对每种强度模型的适用场合进行了讨论。

尽管上述研究已经针对不同体系的复合材料给出了相应的强度分布模型，但是针对陶瓷基复合材料紧固件的强度却尚未涉及。为此本文研究采用PIP工艺制备的C/SiC复合材料螺钉的力学性能，试图找到不同规格螺钉的拉伸强度的分布规律，并建立定量强度分布模型，从而为复合材料许用值的计算提供依据。

1 试验

1.1 试验材料

C/SiC复合材料螺钉采用目前热结构材料广泛使用的PIP工艺[9]制备。其中，碳纤维预制体采用xy向编织、z向穿刺，随后与SiC先驱体，经反复高温浸渍裂解制备而成。制备的材料密度约为1.8 g/cm3，纤维体积分数约为50%；在所有纤维中，z向纤维约占15%，xy向纤维占比相同，共占约85%。

制备了M8、M10、M12三种规格的螺钉，螺钉长度为62 mm，光杆段长38 mm，螺纹段长14 mm。螺牙参照GB/T 197—2003标准，M8、M10、M12三种螺钉的螺距P分别为1.25 mm、1.50 mm以及1.75 mm。采用118胶粘结螺钉与螺母，并在室温下固化24 h。试验中所用的螺钉及螺母宏观形貌见图1。

图1 C/SiC复合材料螺钉外形Fig.1 Macro morphology of C/SiC composite material bolts

1.2 试验参数

拉伸试验在SANS型电子万能试验机上进行，载荷方向为螺钉轴向（x向），加载速率为1 mm/min，试验温度为25℃。采用Quanta FEG 650场发射扫描电镜试样进行微观观察，采用背散射图像对螺钉金相试样进行观察，加速电压为20 kV。图2显示了螺钉轴向不同磨制深度的金相组织。可以看到，加载方向与x向平行，而y向与z向均与加载方向垂直。在加载方向上，z向纤维所占比例较小，除基体外，主要由x向的纤维以及y向界面承受载荷。

图2 C/SiC复合材料螺钉编织结构Fig.2 Structural configuration of C/SiC composite material bolts

2 结果及讨论

2.1 断口形貌

三种规格螺钉的断裂位置均位于自螺帽一侧计第一道螺纹处，断口形貌见图3。从图3（a）中可以看到，C/SiC复合材料断口较为粗糙、且凹凸不平，可见有规律的编织结构。其中，断面上z向纤维约占所有纤维的30%，远大于材料中的z向纤维体积分数（15%）。从图3（b）中可以看到，x向纤维断口整齐，纤维拔出长度较小，呈机械断裂特征；y向纤维附近可见较多呈脆性断裂特征的大块基体；而z向纤维较为整齐，可见纤维表面的沟槽或纤维沟槽在基体上的印痕。图3（c）显示了一束x向纤维的放大形貌，x向纤维与加载方向平行；图3（d）显示了基体的放大形貌，基体材料中存在大量的微裂纹缺陷。

根据上述观察结果可知，z向材料的失效模式以界面脱粘为主，而xy向材料的失效模式以纤维断裂和基体开裂为主。为了达到纤维增韧的目的，复合材料的界面性能应满足界面脱粘能Γi与纤维断裂能Γf之比：Γi/Γf≤1/4[10-11]。此时，z向纤维的界面强度较弱，相当于材料缺陷，因此断裂过程中裂纹容易在z向纤维起源、扩展。当裂纹扩展至xy向纤维之后，继续在y向纤维界面扩展，最终在x向纤维和基体位置发生断裂。值得注意的是，除z向纤维界面外，材料中的裂纹、分层等原始缺陷也可以提供裂纹扩展源区。在纤维、基体以及界面中，x向纤维是主要的承力单元。考虑一束碳纤维的“最弱链模型”[12]，当施加应力超过最弱链的强度时，材料即发生破坏。当材料尺寸增大后，根据“最弱链模型”的假设，遇到某个低强度的材料单元的概率将会增加，因此其破坏概率也将增大，破坏时的强度值相应减小。因此，一束碳纤维的断裂过程满足Weibull统计尺寸效应理论，在脆性材料中有比较好的应用效果。

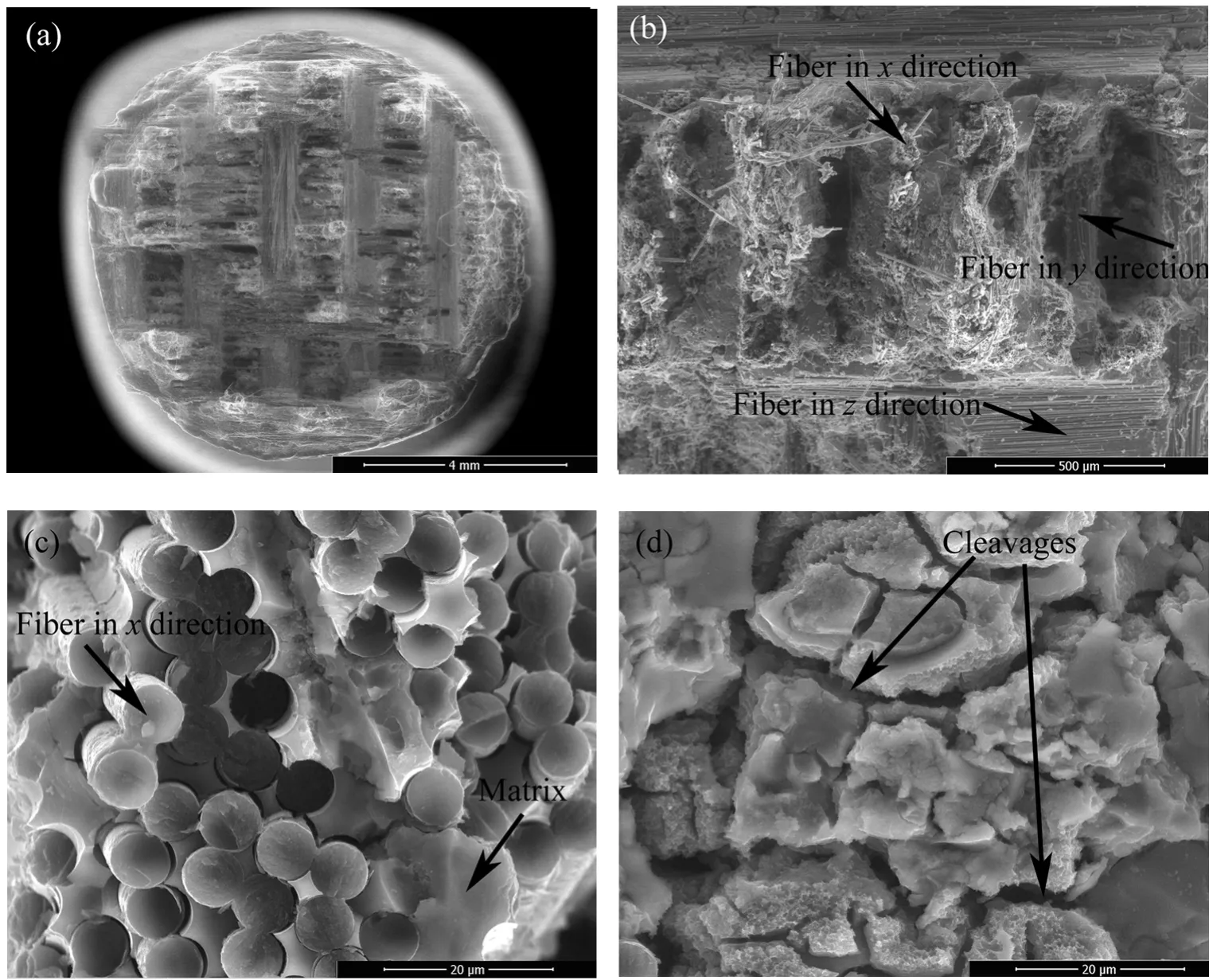
图3 C/SiC复合材料螺钉典型断口形貌Fig.3 Typical fracture morphology of C/SiC composite material bolts

2.2 力-位移曲线

M8、M10、M12三种规格的螺钉典型力-位移曲线如图4所示。

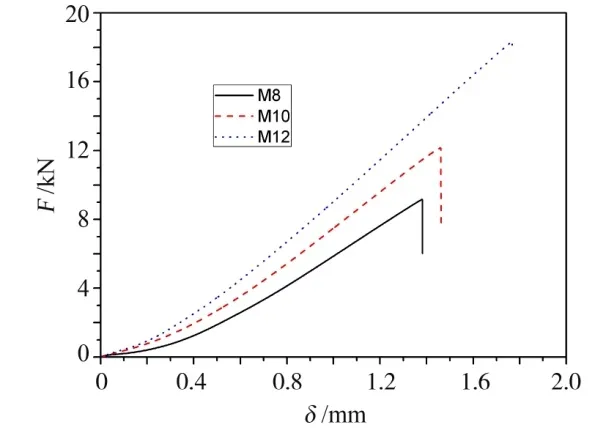
图4 不同规格螺钉典型力-位移曲线Fig.4 Typical force-displacement curves for different types of bolts

可以看到，C/SiC复合材料的力-位移曲线没有明显的屈服段，随着位移的增大，力值大致呈线性上升趋势。上升至最大值后力值突然降低，螺钉瞬间发生断裂。随着螺钉直径的增大，断裂力值增大，且断裂位移也增大。螺钉直径增大，螺钉的承载面积也相应增大，因此断裂力值有增大的趋势。此外，由于复合材料的弹性模量大致相同，因此在拉断力增大的情况下，材料的断裂位移也增大。

2.3 拉伸性能

由于力-位移曲线与螺钉的规格有关，不能有效反映C/SiC复合材料螺钉的强度分布，因此，根据螺钉的拉断力值F和受载面积A计算得到其拉伸强度σc，如式（1）所示：

式中，受载面积A如式（2）所示：

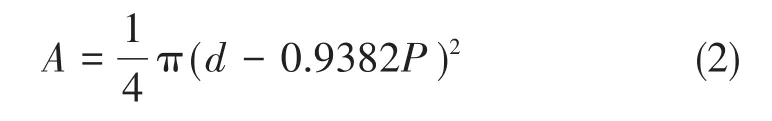
式中，d为螺纹大径，P为螺距。

根据式（1）、式（2）计算得到拉伸强度，如图5所示。可以看出，三种螺钉拉伸强度测试数据在150～250 MPa的窄带当中，但在同样的参数下螺钉的拉伸强度散差较大。事实上，C/SiC复合材料制备过程经过多轮次的浸渍、固化与裂解工序，工艺过程中极易出现局部分层、密度不均，基体微裂纹等缺陷[13]。同时，由于碳纤维和陶瓷基体的强度和模量存在一定差异，加工过程中还会出现基体脱落、纤维拔出等现象，导致材料表面出现微缺陷[14]。加之C/SiC复合材料纤维的编织结构本身会导致材料存在各向异性，因此，材料的强度存在极大的不稳定性。基于此，对于材料的强度分布采用唯象论的办法来解决，仅从试验结果所得的现象出发，越过材料具体的细观和微观结构缺陷，从数据统计的角度给出较为明确的结果。

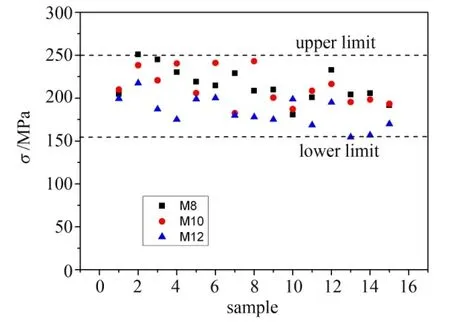
图5 三种类型螺钉拉伸性能测试结果Fig.5 Tensile strength testing results for three kinds of bolts

2.4 Weibull分布模型

大量的实验及其统计分析表明，陶瓷基复合材料强度一般服从Weibull分布。NADARAJAH和KOTZ[8]综述了描述复合材料的强度分布的20余种强度模型，对塑性材料和脆性材料两种情况讨论了不同模型的适用性。他们指出，双参数Weibull模型是描述复合材料强度的最流行的模型，且适用于基体为脆性的材料。M.Alqam等人[15]采用26个纤维增强树脂基复合材料力学性能数据对比了双参数和三参数Weibull模型，他们建议采用双参数Weibull模型来描述材料的性能。该建议的基础是三参数和双参数模型的名义设计值（nominal design values）以及许用载荷（allowable loads）相差非常小，因此采用双参数Weibull模型即可得到满意的结果。CATTELL等人[16]在研究中，发现玻璃纤维增强的树脂基复合材料的拉伸强度也遵循双参数Weibull分布模型。因此，本文采用经典的双参数Weibull分布函数来描述拉伸强度的分布规律，如式（3）所示：

式中，P（x）为强度值不大于x的概率，x为给定的一个强度值。

其概率密度函数p（x）如式（4）所示：

式中，α为Weibull分布的形状参数，β为Weibull分布的尺度参数，其具体的物理意义可以进行如下描述：α表示强度的分散情况，α越大则强度越分散，β表示材料的特征强度，β越大则强度越高。

α和β的参数值可以采用极大似然估计法来估计，满足式（5）和式（6）[17]：

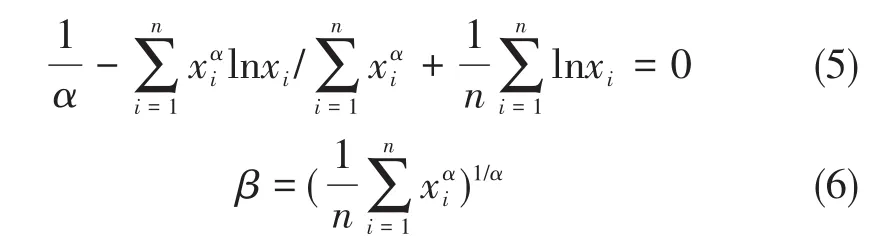
式中，x1，x2，…，xn为强度试验值，n为试样总数。

将试验数据与计算得到的Weibull分布拟合曲线进行对比，结果见图6。从图6（a）中可以看到，Weibull模型中的累积概率分布拟合曲线与试验结果的统计数据较为吻合，而从图6（b）中可以看到，拟合得到的概率密度分布曲线与统计数据的变化趋势一致，表明采用Weibull分布模型描述复合材料强度分布规律是合理的。

2.5 可靠性检验

为了检验得到的Weibull模型的可靠性，选用柯尔莫哥洛夫检验法[18]，验证其是否服从Weibull分布。对给定的显著性水平δ=0.05，当n≤100时，柯尔莫哥洛夫检验的临界值为1.36。将试验数据x1，x2，…，xn按照不降次序重排，并为了方便起见仍记为x1，x2，…，xn，则可按式（7）、（8）计算Dn：

若Dn≤1.36/则Weibull分布模型通过柯尔莫哥洛夫检验。根据式（7）、（8）中的计算结果，可知Dn=0.090，因此试验数据通过柯尔莫哥洛夫检验，数据最大偏差为9.0%。

根据Weibull模型中得到的双参数计算结果，对复合材料设计许用值X进行计算，如式（9）所示[17]：

许用值X与可靠程度R的相对关系见图7。可以看到，对复合材料要求的可靠性越高，设计许用值就越低，例如，在80%的可靠度下，C/SiC复合材料设计许用值为180 MPa。因此，可以根据Weibull分布所预测的材料强度值来进行材料选择和结构设计。

图7 在不同可靠程度下的设计许用值Fig.7 Allowable strength at different reliabilities

3 结论

（1）对M8、M10、M12三种规格的C/SiC复合材料螺钉进行了拉伸性能试验，发现螺钉断裂位置位于自螺帽一侧计第一道螺纹处，其力-位移曲线没有明显屈服段，随着螺钉直径的增大，拉断力值增大，断裂位移也增大。

（2）对M8、M10、M12三种规格的C/SiC复合材料螺钉拉伸强度进行了统计分析，发现C/SiC复合材料螺钉拉伸强度满足双参数Weibull分布模型，其特征强度β为212 MPa，形状参数α为9.45，试验数据与模型预测数据最大偏差为9.0%。