一种LT码度分布优化方法

姚渭箐 胡 凡

（1.国网湖北省电力有限公司信息通信公司，武汉，430077；2.武汉大学电子信息学院，武汉，430072）

引 言

喷泉码是一类纠删码[1,2]，具有无需反馈重传、无码率性、兼容性强和编译码复杂度低等特征，已广泛应用于深空通信[3]、认知无线电[4]、物联网[5]和云存储等领域[6]。2002年，Luby提出了第一个喷泉码的具体实现方案——LT(Luby transform)变换码[7]，完成了对LT码的编译码算法及度分布构造的基础研究，其中最重要的贡献是完成了对鲁棒孤子分布(Robust soliton distribution,RSD)的推导及分析。

RSD也存在一定局限性，在一些实时性要求较高的应用中，例如视频图像传输，为提高传输速率需尽量减小码长。然而，在短码长构造下RSD的译码性能较差，需要较大的译码开销才能译码成功。针对该问题，国内外诸多学者和科研机构在LT码的度分布优化问题上做了大量研究工作。

文献[8,9]分别采用粒子群优化算法(Particle swarm optimization,PSO)和蚁群算法(Ant colony algorithm,ACA)对LT码度分布进行优化。将度分布中度数的比例值映射到仿生算法的解空间构建初始路径，经过仿生算法迭代优化，从一定程度上能够得到相同度分布参数要求下更优的度分布值。文献[10]将二进制指数分布(Binary exponential distribution,BED)和RSD相结合提出一种译码性能更优的开关度分布(Switch degree distribution,SDD)。在编码器编码的初始阶段，采用BED进行编码，当已经产生一定数量编码分组后，将BED切换到RSD。文献[11]基于置信传播(Belief propagation,BP)算法的AND-OR分析，将度分布优化问题转化为半正定规划(Semi-definite programming,SDP)形式，随后又转化为一个线性规划问题。文献[12]引入加权系数将改进的泊松分布(Improved Poisson robust soliton distribution,IPD)和RSD联合成一种适用于LT码的联合泊松鲁棒孤子分布(Combined Poisson robust soliton distribution,CPRSD)。并基于期望可译集特性，采用黄金分割点算法对加权系数进行寻优。

尽管现有的度分布优化方案已取得一定研究成果，但仍然存在提升的空间。为了得到更优的度分布，本文基于度分布重要特性，采用人工鱼群算法(Artificial fish swarm algorithm,AFSA)对RSD中某些重要度数的比例进行寻优。仿真结果证明，在二进制删除信道(Binary erasure channel,BEC)中，采用优化后的度分布对短码长LT码进行编码，能有效降低译码开销，并节约编译码耗时。

1 LT码及度分布

1.1 LT码编译码过程

LT码的编码过程非常简单，具体如下：

Step 1从度分布中随机选择一个度i；

Step 2随机且均匀地选取i个原始分组；

Step 3将这i个原始分组进行异或生成一个编码分组。

重复以上步骤，编码生成无限且灵活数量的编码分组。

接收端接收到N个编码分组(N略大于k)，然后开始译码[7]。通常，LT码采用BP算法进行译码。

Step 1度数为1(i=1)的编码分组直接译码；

Step 2译出的原始分组与跟其相连的编码分组进行异或后替代原编码分组，同时删除其连接关系。

重复以上步骤，直至译码完成。LT码编译码过程如图1所示。

1.2 度分布

根据LT码编译码过程可知，度分布对LT码的性能影响至关重要。文献[7]指出，一个好的度分布需满足两个设计目标：（1）译码成功所需的平均编码分组数量尽可能少，确保LT译码成功的编码数量对应于确保原始分组全部译出的编码分组数量。（2）编码分组的平均度数尽可能小，平均度数是生成一个编码分组所需的平均异或运算次数，因此，平均度数决定了编码复杂度，而译码复杂度则是平均度数乘以译码成功所需编码分组数量。

最经典的是Luby在2002年提出的RSD[7]，其表达式如下

图1 LT码编译码过程Fig.1 LT encoding and decoding process

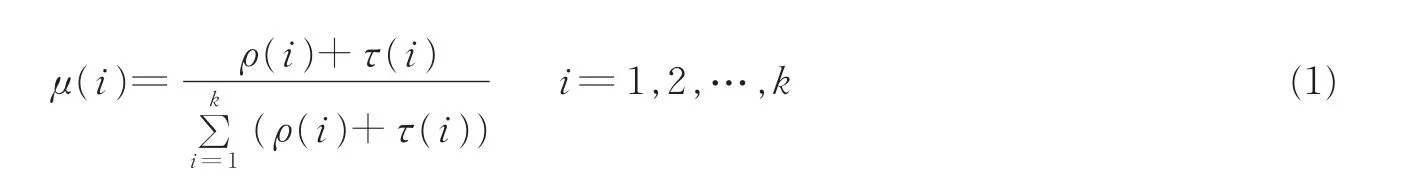
式中

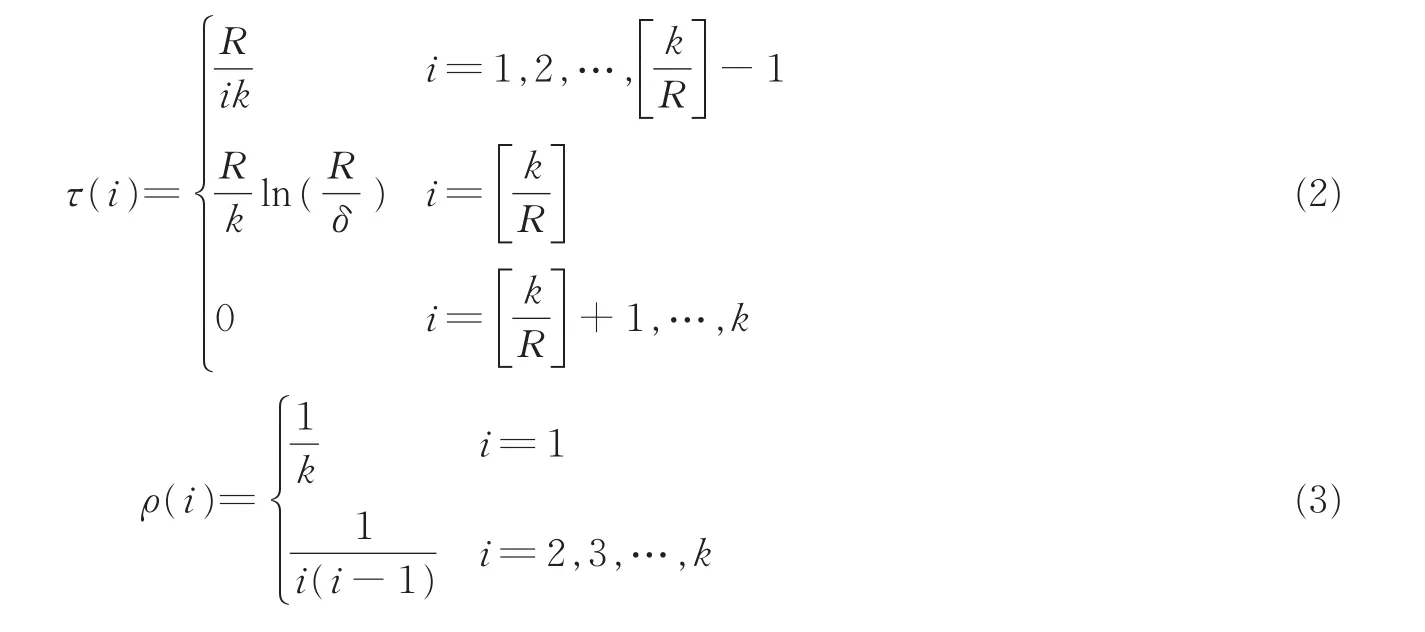
RSD函数最后的“Spike”τ(k/R)能保证编码过程中高效地覆盖所有原始分组。

1.3 度分布重要特性

度分布中某些度数对LT码可译码性的影响至关重要，通过调整这些度数在度分布中的比例，LT码可获得良好的性能。首先，度数为2在度分布中所占比例最高，当k→∞时，该比例趋近于1/2[13]。其次，需要度数为1的编码分组来触发BP译码开始，意味着度数为1的比例大于0。但是，过多的度数为1的编码分组会造成低效译码，也就是说，度数为1的比例必须要小。可以发现，好的度分布都具有一个共性，即度数为1的比例远小于度数为2的比例，否则，会导致一个相当大的最小译码开销[14]。

2 基于人工鱼群算法的度分布优化方法

基于度分布重要特性，对RSD进行改进。采用AFSA对RSD中度数为1、度数为2以及度数为k/R的比例进行寻优，从而得到相同度分布参数要求下更优的度分布。

AFSA[15]是一种模拟鱼群的觅食、聚群、追尾等典型行为在搜索域中实现寻优的智能进化算法。人工鱼对视野范围内的环境进行感知，即模拟群聚行为和追尾行为，然后进行行为评价，选择最优者来实际执行，默认行为方式为觅食行为。

2.1 寻优原理

基于AFSA度分布寻优的核心是：首先，将度分布中度数为1、度数为2以及度数为k/R的比例值映射到AFSA的解空间构建初始值；接着，基于平均度数构建该算法的目标函数；然后，通过比较和迭代逼近最大目标值从而获得优化的度分布。

（1） 初始值产生

重要度数的比例对应一个人工鱼的状态为Ω=(Ω(1),Ω(2),Ω([k/R]))。基于度分布特性和RSD(μ(1),μ(2),…,μ(k))产生人工鱼初始值

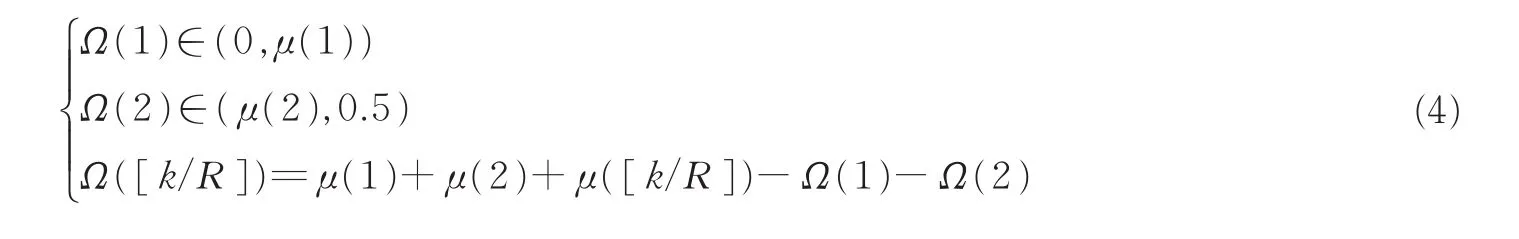
（2） 目标函数构建

为降低编译码复杂度，希望编码分组的平均度数尽可能小[7]。由于非重要度数的比例保持不变，因此，将度分布优化问题转换为最小化Ω(1),Ω(2),Ω([k/R])的平均度数，即通过最小化式（5）来获得优化度分布

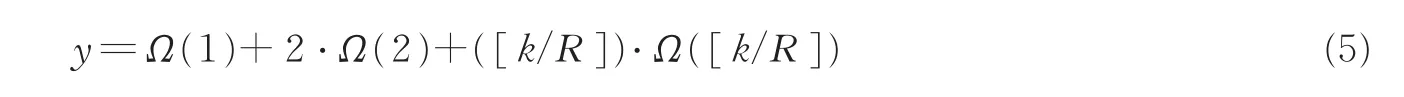
（3） 人工鱼群算法

度分布优化问题的解决是通过人工鱼在寻优过程中以局部最优和个体最优形式表现出来的。寻优的过程中，跟踪记录最优个体的状态，该过程可通过模拟人工鱼追尾行为来实现。追尾行为有助于快速地向某个极值方向前进，可防止人工鱼在局部振荡而停滞不前。随着寻优过程的进展，人工鱼往往会聚集在极值点的周围，并且全局最优的极值点周围通常能聚集较多的人工鱼，该过程可通过模拟人工鱼聚群行为实现。在对追尾行为和聚群行为进行评价后，自动选择合适的行为，从而实现对度分布高效快速的寻优。基于AFSA度分布寻优原理如图2所示。

具体人工鱼行为描述如下。

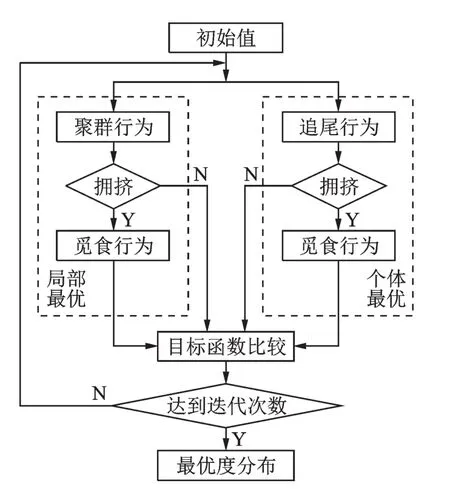
图2 基于AFSA的度分布优化模型Fig.2 Optimization of degree distribution based on AFSA

（1）视觉模拟(逼近搜索)：设一个人工鱼的当前状态为Ω=(Ω(1),Ω(2),Ω([k/R]))，在搜索域(Visual)内进行随机搜索，如果感知到更优状态Ω'=(Ω'(1),Ω'(2),Ω'([k/R]))，则朝该状态的位置方向前进一步；否则，继续搜索。该过程可以表示为

式中：Rand∈(-1,1)，S为最大移动步长。

（2）聚群行为(局部寻优)：设人工鱼当前状态为Ω，在Visual内随机搜索聚集成群的ny个人工鱼，并定位这ny个人工鱼间的中心位置Ωc，如果yc/ny＞d⋅y(d为拥挤度因子，表示与其他人工鱼之间的拥挤情况)，表明该位置为局部最优位置，则根据式(7)，朝Ωc方向前进一步；否则执行觅食行为。

（3）追尾行为(个体寻优)：设人工鱼当前状态为Ω，在Visual内随机搜索ny个人工鱼，并定位其中yj为最小的Ωj，如果yj/ny＞d⋅y，表明该状态为个体最优，则根据式(7)，朝Ωj方向前进一步；否则执行觅食行为。

（4）觅食行为(随机寻优)：设人工鱼当前状态为Ω，在视野范围内随机搜索一个状态Ωj，如果y＞yj，表明该状态优于当前状态，则根据式(7)，朝Ωj方向前进一步；反之，再重新搜索。反复试探多次后，如果仍无法定位更优状态，则根据式(6)，随机移动一步。

2.2 寻优步骤

Step 1基于RSD产生初始鱼群，例如，鱼群大小为m，有3个待优化的参数，即Ω=(Ω(1),Ω(2),Ω([k/R]))。 其 中 ，Ω(1)∈(0,μ(1))，Ω(2)∈ (μ(2),0.5)，Ω([k/R])=μ(1)+μ(2)+μ([k/R])-Ω(1)-Ω(2)，则要随机产生一个3行m列初始鱼群{Ωv|v=1,2,…,m}。

Step 2每个人工鱼执行群聚行为得到局部最优值，执行追尾行为得到个体最优值。

Step 3通过行为评价，即比较两种行为的目标函数值，选取函数值较小者作为一个人工鱼的最优值yvmin及其对应的Ωvmin。

Step 4m个人工鱼完成一次感知行为得到{y1min,y2min,…,ymmin}及其对应的{Ω1min,Ω2min,…,Ωmmin}，再比较m个人工鱼目标函数值，选取函数值最小者作为人工鱼群的最优值，得到ymin及其对应的Ωmin。

Step 5将ymin与前一次的最优值进行比较，得到一次迭代的最优值ybest及其对应的Ωbest，如果迭代次数小于设定值，转移到Step 2，否则寻优完成，得到全局最优目标函数值ybest及其对应的人工鱼状态Ωbest。

优化后的Ωbest(2)的比例有所增加且满足Ωbest(1)≪Ωbest(2)，符合度分布通用特性[14]，可降低恢复所有原始分组所需的最小译码开销。而此时，Ωbest([k/R])仍然保持较高比例，从而保证编码过程中高效地覆盖所有原始分组。并且，由于平均度数降低，意味着编译码过程中进行的异或运算量大大降低，从而加快编译码速度。因此，即使在码长较短(原始分组数k＜104)时，也能保证较好的译码性能和编译码效率。

3 性能仿真及分析

为验证所提方法的有效性，根据参考文献[12]，选取相同参数k=1000，c=0.1，δ=0.005时，分别对本文改进的RSD(Modified RSD,MRSD)、参考文献[8-10]中的度分布设计方法和RSD进行1000次编译码仿真，然后对实验结果进行比较和分析。AFSA算法中对各参数的取值范围比较宽容，并且对算法的初值也基本无要求[15]。根据每个度值的初始值约束范围，经过多次实验选取AFSA参数为：人工鱼数量为m=50个，试探次数为100次，迭代次数为50次，Visual=0.001，d=0.618，S=0.0005。仿真实验平台为Intel(R)Core(TM)2.8 GHz处理器，4 GB内存。采用Matlab R2014a编程仿真。

MRSD及其他4种度分布的译码成功率随译码开销((N-k)/k)变化情况如图3所示。译码成功率为译码器接收不同数量的编码分组时，成功译出的分组数占原始分组总数的比例。从图3可以明显看出，传统的RSD不太适用于短码长LT码。RSD初始译码成功率较低，并需要50.7%译码开销才能完全恢复k=1000原始分组。而MRSD译码性能最优，不仅初始译码成功率较高，并随着接收编码分组数的增多，译码成功率快速上升，达到恢复k=1000原始分组时的译码开销仅为25.2%。与其他3种优化度分布相比，MRSD译码性能也是最优。

表1对5种度分布的译码成功所需的平均译码开销、平均度数以及单次编译码耗时进行比较。当k=1000时采用MRSD度分布进行LT编码，译码成功所需的平均译码开销比其他4种度分布降低了5.7%～25.5%，并且节约了至少8.5%(8.5%～44.9%)的平均编译码耗时。

为获得更为直观的对比结果，采用256×256×8=524288 bit的灰度图作为传输数据。将原始数据均分为1024个原始分组(每个原始分组包含512 bit)，当接收端接收到1200个编码分组时强制译码恢复，对图像的恢复质量进行直观评估，结果如图4所示。从图4中明显看出，RSD以及其他3种优化度分布恢复的图像都存在不同程度的失真，而MRSD度分布几乎完全恢复图像。

图3 不同度分布译码性能(k=1000,c=0.1,δ=0.005)Fig.3 Decoding performance fordifferent degree distributions

表1 不同度分布性能比较（k=1000，c=0.1，δ=0.005）Tab.1 Performance comparison for different degree distributions（k=1000，c=0.1，δ =0.005）

图45种度分布图像恢复质量比较Fig.4 Image recovery for five degree distributions

4 结束语

针对RSD在LT码码长较短时性能不够理想的情况，本文提出一种适用于BEC信道的度分布优化方法。基于度分布特性和AFSA，通过调整度分布中某些重要度数的比例，从而提高短码长LT码的译码性能。基于原始分组k=1000的仿真结果表明，与传统的RSD及类似方法相比，采用所提出的方法优化度分布更能有效提高短码长LT码的编译码效率和译码成功率。