2019年天津市中考压轴题的解法探究与反思

宋 春，刘金英，赵国华

（天津市滨海新区塘沽第六中学；天津市教育教学研究室；天津市滨海新区塘沽教育中心）

《普通高中数学课程标准（2017年版）》明确提出了发展学生六个数学核心素养的课程目标.在考试评价中，考查学生的核心素养已成为高考和中考命题的新导向.2019年天津市中考数学试卷压轴题在核心素养方面有明确体现.

一、试题呈现

题目（2019年天津卷第25题）已知抛物线y=x2-bx+c（b，c为常数，b＞0）经过点A(-1，0)，点M(m，0)是x轴正半轴上的动点.

（1）当b=2时，求抛物线的顶点坐标；

（2）点D(b，yD)在抛物线上，当AM=AD，m=5时，求b的值；

二、解法探究

1.第（1）小题解法分析

因为抛物线y=x2-bx+c经过点A(-1，0)，所以1+b+c=0，即c=-1-b.当b=2时，y=x2-2x-3=(x-1)2-4，所以抛物线的顶点坐标为(1，-4).

【评析】这一问的起点较低，代入坐标消参数即可.学生应养成仔细审题的习惯，注意题中给出的抛物线解析式的一次项系数是-b.同时这里的“消元”为后续解题做了铺垫.

2.第（2）小题解法分析

由（1），得c=-1-b.将点D(b，yD)代入抛物线解析式，得yD=-b-1.则点D的坐标为D(b，-b-1).

之后有三种不同的方法.

方法1：由AM=AD，根据两点间距离公式，得.解得（舍），.

方法2：因为b＞0，所以点D(b，-b-1)落在第四象限.如图1，过点D作DE⊥Ox于点E，由AM=AD，得AM2=AD2.根据勾股定理，得(b+1)2+(-1-b)2=62.解得（舍），.

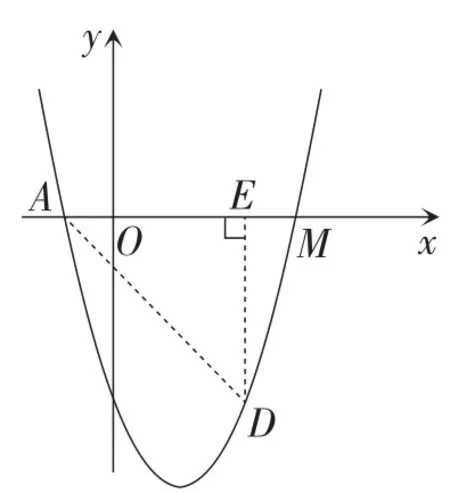
图1

方法3：如图1，由D(b，-b-1)，可知AE=b+1，DE=b+1.得△ADE为等腰直角三角形.所以.由AD=AM，得.所 以.解得.

【评析】第（2）小题中的二次函数解析式中含参数b，c，首先想到消掉参数.此问着重考查学生的消元和计算等能力，运用了数形结合思想、转化思想、函数思想、方程思想等.

3.第（3）小题解法分析

方法1：如图2，以AM为直角边构造等腰直角三角形PAM，延长MQ到点M′，使得QM′=MQ.

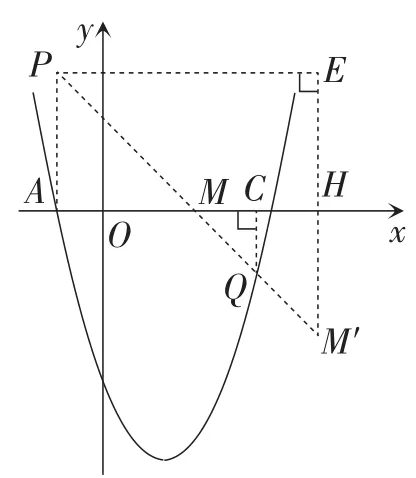
图2

方法2：如图2，当PM与MQ共线时，

分析：由取最小值，可以把问题转化为提取系数2，得.再求的最小值即可.

方法3：过点Q作QH⊥Ox于点H，过点M作MG⊥AG于点G，构造∠MAG=45°，当G，M，Q三点共线时，QG的长最短，即最短.

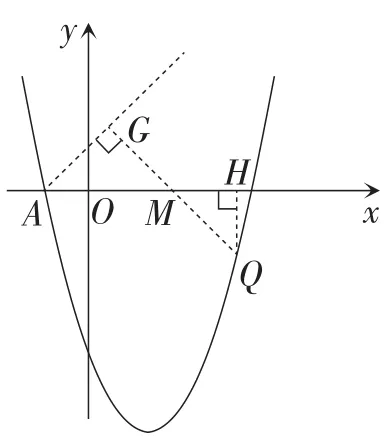
图3

此方法还可以做进一步优化.

如图4，延长QH，交AG的延长线于点E，

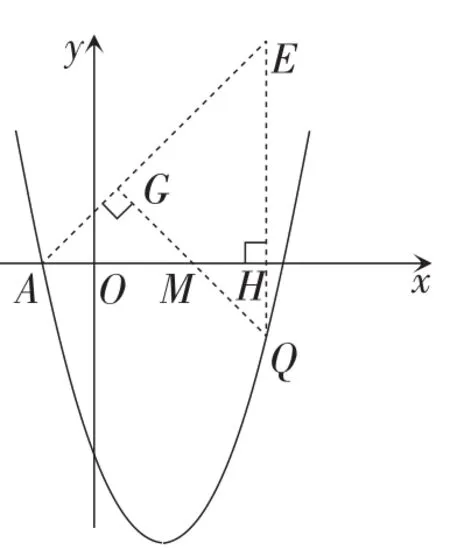
图4

图5

解得b=4.

【评析】这一解法将方法3进行变式，借助轴对称变换，使点Q的位置发生变化，再利用点到直线的距离公式，可以优化计算.

图6

此题第（2）小题运用数形结合、勾股定理、三角函数、两点间距离公式等，借助点D和点A的坐标进行消元，解法自然，思路清晰.第（3）小题以的最小值为切入点，考查了图形与坐标、图形与几何、图形与变换的内容.《义务教育数学课程标准（2011年版）》指出：数学课程内容不仅包括数学的结果，也包括数学结果的形成过程和蕴涵的数学思想方法.此题既立足于基础知识，又关注过程与方法，同时又凸显学生的思维.

第（3）小题在第（2）小题的基础上，增加动点M，增加了求线段之和最小值的问题，具有一定的难度，转化思想变得尤为重要.方法1采用直接构图的策略，用到等腰直角三角形三边之比（或三角函数）、线段加倍、中点坐标公式等，找到取得最小值的求法；方法3转化比值更直观，计算更巧妙；方法3和方法5巧提系数，使得构图更方便.探寻本质，几种方法均是求线段之和最小值的问题，其转化的实质是“两点之间线段最短”或“垂线段最短”.第（3）小题思维含量高，综合能力更强，对学生的转化能力要求较高.

可见，题目中的三道小题的设计由浅入深、环环相扣、构思巧妙，且内涵丰富、综合性强，具有较高的思维含量.正如庞加莱写到：数学家非常重视他们的方法和理论是否优美.数学题的构造和解法，不仅使人心情愉悦，更能让我们对整体和细节都有清楚的认识，更好地把握问题的本质.

三、几点思考

1.遵循课程目标，引领教学方向

随着课程改革的深入，中考命题设计更加注重“四基”、着眼能力、关注素养、立足发展，既体现了数学学科本质，又有效遏制了题海战术，减轻了学生的学业负担，达到了提升考试正导向的作用，引领教学方向.此题三道小题环环相扣，层层深入，有“曲径通幽”之美.

2.关注过程方法，凸显学生思维

第（3）小题可以从不同的视角下加以分析，既考查思维的过程与方法，又考查学生的空间想象能力，凸显思维的灵活性.日常教学中，教师要重视对新知识、新概念、新方法的探究过程，多组织有效的数学活动，多为学生创造参与数学活动的机会，多让学生经历知识的形成和应用过程，这样才能提高学生的数学探究能力，最终达到发展学生思维能力的目标.

3.强调几何直观，助力能力提升

第（2）（3）小题特别突出对学生的几何直观能力的培养.借助几何直观可以将复杂问题变得简明、形象，有助于学生探索解决问题的思路，预测结果.合理的构图可以把复杂问题简单化，这是对学生数学能力的升华.借助几何直观进行教学，可以形象生动地展现问题的本来面目，有助于促进学生对数学的理解，在渗透数学思想方法的同时，提高学生的思维能力和解决问题的能力.几何直观常常表现为对于某种解题思路或方法的顿悟，进而促使学生的能力产生质的飞跃.

4.注重数形结合，体现数学本质

从此题的解答过程中，可以看出：第一，已知条件不只在题意当中有，在图象中也会有，需画出恰当的图象；第二，对含参数的二次函数的解析式，一定要注意挖掘其中的隐含信息，如过已知点或图象过某一定点等，此时“消元”就显得尤为重要；第三，对于含参数的函数解析式，其图象一定是动态的，但动中有静，动是运动的过程，静是运动的结果，静就是图形运动到特殊位置，就会显示特殊的关系；第四，以“点”为依托，通过几个特殊位置的点搭建“线”和“形”的关系，数形结合思想、模型思想才会得以充分体现.

5.加强数学应用，彰显核心素养

核心素养的养成，不能单纯依赖教师的“教”，而是需要学生参与其中的；不能单纯依赖记忆和模仿，而是需要学生的感悟与体验.学生的自主学习、主动探究的学习方式，教师的启发引领式的教学等，均需要教师设计科学合理的问题进行引导.此题可以启发学生思考，让学生在应用数学知识的同时，感悟数学的本质，积累分析问题和解决问题的经验，使核心素养的形成和发展真正落地、落细、落实.