使用分析法发现命题证明思路探究

张 昆

（淮北师范大学数学科学学院）

平面几何证明表达的特点是使用符号语言，形成言简意赅、顺理成章的结论，组成证明的表达结论和形式具有环环紧扣，言之凿凿，以及令人信服的特点.这种谨严的逻辑性，使学生可以非常直观地感受到公理化思想说服自己或他人的力量.在学习命题证明的过程中，正是这种公理化逻辑特点的严谨性决定了在一般情况下，有些学生对于稍微复杂一点的命题，不能一次性地达到目的.于是，在学生学习平面几何证明的过程中，发展学生的基本探究证明思路的方法是至关重要的，其中分析法是探究证明思路入门的首要方法.

一、分析法的内涵

在谈到分析法时，伟大的英国物理学家、数学家牛顿指出：一般说来，从结果到原因，从特殊原因到普遍原因，直到论证止于最普遍的原因，这就是分析的方法.张乃达先生认为：分析就是将研究对象的整体分为各个部分、方面、因素和层次，并分别加以考察的认识活动.由此可知，分析法就是使用执果索因的过程进行表征的方法.简单地说，分析法就是从所要证明的命题结论出发，以这个结论为起点探究证明思路的方法.分析是从未知向已知化归的手段，分析在平面几何证明中的作用在于通过分解、析取等步骤和操作，实现未知与已知的联系，即将未知的内容归结为已知的内容，从而为综合创造条件.

因此，从形式上看，分析法的使用途径是执果索因，即寻找产生某种结果的原因（条件）的方法.其基本思想是由未知（“果”）探求需知（“因”），如此，环环紧扣地逐步向前搜索，直到最后一个需知就是题目中的已知，解决问题的思路就已经出现了，探究活动可以终止了.在探究平面几何证明思路时，分析法的巧妙作用就在这里.本文以研究平面几何命题证明入门的教学为例，探讨促使学生体验分析法在探究平面几何命题证明思路中的作用.

二、分析法在探究平面几何证明思路中的应用示例

笔者在长期从事平面几何证明的教学实践中观察得到以下结论：初中生在学习平面几何证明时，只关注定理（或公理）及其逻辑推理的结论，学习的结果往往是记忆性的，而不是理解性的.他们对定理的字、词、形的表达结构层次难于精确把握，这就导致其在应用定理（或公理）进行推理论证时，对问题结构层次的理解出现错误.例如，分不清楚命题的题设和结论，作不出比较准确的几何图形等.以上因素导致了学生学习难，教师施教难.那么，在教学平面几何证明时，教师应该从哪些方面努力呢？

笔者在多年的教学实践中，发现了学生在探究平面几何证明思路时的疑难症结所在，并且从中认识到：平面几何证明题所要求证的结论最终都能转向已知，但是，学生在寻找组成证明逻辑环节的这些已知时，对于稍微复杂一点的命题，不可能一次性地成功达到目的，而是要配合所用定理（或公理）首先寻找出需知，利用这些需知来调控已知对结论的决定性作用.由此得到，在初学平面几何证明时，从命题的结论出发探究需知的过程是学生最容易接受的，而这种探究过程便是分析法的要旨之所在，也是教师实现有效教学的最佳手段之一.

追根溯源，教师在平面几何命题的推理论证教学中，通过与学生进行“心理换位”，站在学生的立场上，合理地引入分析法，可以将那些处理题设条件时头绪纷繁、错综复杂的元素关系变为比较线性化的元素关系，向学生提供有效的探究命题证明思路的手段，从而降低学生的逻辑推理强度，减轻探究难度.如此，分析法对于教师施教和学生学习平面几何推理论证的内容，都大有裨益.

陆游诗曰：纸上得来终觉浅，绝知此事要躬行.教学中，教师在探究平面几何推理论证的解题思路时，一定要通过选择典型例题，选择合理的课堂教学方法，从而将这些例题有效地作用于教学，实现教学目的，进而经由教学活动，促使学生在平面几何证明过程中形成使用分析法的数学思想.在教学中，教师通过教学分析法设计活动，使学生经由努力可以很好地掌握证明思路.

我们看一个利用分析法探究平面几何证明思路的例子.

证明：对角线互相垂直的梯形两底之和小于两腰之和.

关于这种文字性的证明题，解题时可以分为四个步骤：第一步，依据题意，画出符合要求的几何图形（如图1）；第二步，依据图形，将数学语言转化为符号语言：在梯形ABCD中，AD∥BC，AC⊥BD，求证：AD+BC＜AB+DC①；第三步，依据图形与符号语言探究证明思路；第四步，写出严谨的证明过程.

图1

教学片断如下.

师：大家能够找到证明这个命题的思路吗？

生：……

注：师生对话过程中的省略号表示学生思维的暂时中断.

师：大家仔细地对照图形，思考要证明的结论式①的表达与图1中的哪些要素有联系？

生1：结论式①的左右两边都是两条线段之和，从而导致了比较大小的困难.如果将它们都转化为一条线段的话，比较大小就会容易得多.可惜的是，我没有找到转化的途径.

师：生1所产生的将两条线段之和转化为一条线段的想法应该是有效的，是一种很好的想法，可惜他没有找到合适的转化途径.大家再仔细思考一下，可以部分地实现这种转化吗？

生2：结论式①的左边AD+BC是这个等腰梯形的两底之和，通过这个事实，引进梯形的中位线，就可以将AD+BC转化为这条中位线长度的2倍.如图2，取AB的中点E，DC的中点F，连接EF，OE，OF，则②，……

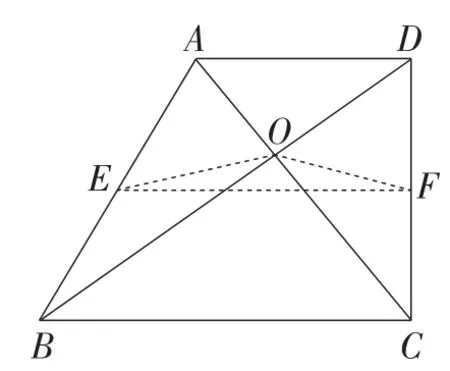
图2

师：生2成功地转化了要求证的不等式①的左边.遗憾的是，结论式①的右边没有被转化掉，致使没有一举解决这个问题.下面大家可以将思考的重点放在不等式①右边的两条线段上了，思考如何将线段AB+DC转化为一条线段，或者将线段AB，DC单独转化为其他线段？

生3：我发现了.由于△OAB与△ODC是直角三角形，而OE，OF分别是△OAB与△ODC的斜边上的中线，从而知③，④，于是，由③④②①知，只要证明OE+OF＜EF就行了，这是明显成立的.

师：如何根据大家探究的思路给出严格的证明表达呢？

师生总结证明过程如下.

证明：如图2，取AB的中点E，DC的中点F，连接EF.

因为EF是梯形ABCD的中位线，

又因为OE，OF分别是△OAB与△ODC的斜边上的中线，

在△OEF中，知EF＜OE+OF.

所以AD+BC＜AB+DC.

综合上述示例的解决过程，不难发现，证明过程的严谨性只不过是将分析探究思路过程的结论精致化的过程.学生不能进行有效地分析由结论到需知再到已知的过程，有效的证明活动过程就不会产生.在探究这一平面几何题证明思路过程中发现，从这个命题的结论出发，一步一步追溯结论成立的原因（条件、替身），直到论证止于最普遍的原因（条件、替身），最终找到证明思路，为成功地进行证明的表达活动打下了基础，由此，可以发现分析法在探究平面几何证明思路中具有举足轻重的作用.

在寻找平面几何证明题的思路时，对于稍微复杂一些的题设条件，对于初学者而言，有时似乎只是随手抓来一些颜料，不分青红皂白地乱涂乱抹，这些涂抹彼此之间似乎毫无关系.可是，在教师的精心设问和启发下，可以促使学生对这些胡乱的涂抹离得远一些.再一看，大致就会得到一个奇怪的印象：摆在你面前的竟是一条通向题目结论的途径.这就令人玩味不已，愉快的心境便油然而生.教师必须在这方面最大限度地做出努力，从而发挥自己的主导作用.

教学具有科学性，更具有艺术性.艺术是凭借技巧、意愿、想象力、经验等因素的融合与平衡，与他人分享美的感觉或有深意的情感与意识，艺术很难通过教师讲授就能获得.它是在领悟、反思与实践的过程中的协调、平衡与统一.现代数学教学理念提倡“以人为本”，这就要求教师学会与学生进行“心理换位”，即要基于学生的心理立场思考问题，要不断地对自己提问.例如，这样教学能引导学生积极参与教学过程吗？能让学生感受数学的价值吗？能使学生愿意学、喜欢学，对数学感兴趣吗？探究平面几何证明思路的分析法就是在这种师生、生生对话之间萌生的，是学生在教师或学生之间的相互启发下实现的，平面几何由于具有直观图形的支持，使得学生理解分析法具备了非常好的载体.

三、结束语

关于平面几何推理论证的教育价值.阿兰说得好：“几何学，是自然的钥匙.谁不是几何学者，谁就永不明了他所生活和依存的那个每天都要面对的世界.他在对抗力量面前，会宁凭一时热情去梦想，自弃自骗，衡量失当，估计错误，这就有可能受害，可能陷入不幸.因而，我决不同意什么都要教授全部自然.不，不是这样，而是要根据客观，按照清晰可见的必然来校正精神.不要多，也不可少.那没有一点几何必然观念的人，甚至会缺乏外部世界必然观念.而全部物理学和外部自然史统统加起来也给不了他一丁点儿必然观念.”平面几何命题证明是培养理性思维的最为重要的环节之一.教师在教学研究中，要对教学内容的重、难点进行认真、深入地思考，引导学生分析探究，透过图形的表象，发现图形某些关系之间的本质，使学生的几何推理论证思维结构不断形成.