横向剪切及伸缩变形对层合板振动特性的影响分析

叶天贵， 靳国永， 刘志刚

(哈尔滨工程大学 动力与能源工程学院，哈尔滨 150001)

为了满足不同工程需求，具有比刚度高，比强度大，可设计性强等特点的层合板应用十分广泛。例如，层合板常应用于舰船桅杆、烟囱、整体上层建筑等[1]；波音787客机机体结构大量应用由碳素纤维经聚合物灌注而成的碳素层合板和由两层纤薄硬质蒙皮附着在蜂巢核芯上制成的碳素夹芯结构，重量占比达50%以上。

在层合板的制造和使用过程中，除了涉及复合材料工艺和设计外，还涉及大量的建模计算分析问题。关于板结构的力学建模研究可以追溯到19世纪。19世纪中叶，Kirchhoff提出了经典薄板理论。20世纪初，Mindlin在经典薄板理论的基础上进一步考虑了横向剪切变形的影响，提出了中厚板理论。这两大理论构成了板结构两大支柱理论[2-5]。经典等效单层板理论和剪切变形板理论是传统板理论在层合板上的直接推广应用。这两种理论先在厚度方向上把层合板等效成各向异性的单一薄层结构，然后用这一薄层的位移或者应力分量描述结构的整体力学行为。因此，当结构的厚度比较大或者各铺层材料性质差异较为明显时，层间位移连续但不满足层间应力连续条件的上述两种二维简化理论产生的建模偏差急剧增大。为解决这一问题，舒小平[6]，Cho和Kim[7]，Murakami[8]，Di Sciuva[9]等提出了一系列锯齿理论。然而，锯齿理论位移形式往往十分复杂，而且位移函数往往没有明确的物理含义，理解起来比较困难。同时，大部分锯齿理论都是针对特定铺层层合板推导得到的，不具有普适性[10]。

在一些对结构振动要求严格的高科技领域，如航空航天、国防装备和微型机械系统，高性能层合板的大量应用经常要求对其振动行为作精细的计算和分析。此时，建模精度过低的二维简化理论往往满足不了要求，需使用更为精确的三维理论来建模分析。对于层合板振动而言，只有至少一对边简支、铺层方式正交的层合矩形板才具有三维弹性解析解，而对于其它结构形式、边界条件和铺层方式只能借助数值或者近似解法。因此，建立一般边界条件和铺层方式下层合板振动问题三维求解方法具有重要的实际意义。

本文基于广义谱方法和微分求积法提出了一种适用一般边界条件和铺层方式的层合板振动三维解法。在此基础上，系统研究了不同边界条件及铺层方式下横向剪切及伸缩变形对层合板振动特性的影响。本文旨在为层合板振动特性分析提供了一种新的计算方法。文中数据还可用于检验各种简化理论的适用性。

1 理论建模

1.1 层合板结构模型

如图1所示，取一长为a，宽为b，厚度为h的层合板。建立如图所示的右手正交坐标系oxyζ，其中x和y为板底面的两个坐标方向，ζ为板的厚度方向。该层合板由任意K层具有不同厚度和材料性质的复合材料或者各向同性材料层紧密复合而成。其中，ζk和ζk+1分别表示第k子层下表面和上表面的横向坐标，hk为该层厚度，ϑk为该层材料坐标与几何坐标之间的夹角。

图1 层合板几何模型及坐标系统Fig.1 Geometry dimensions and cartesian coordinate system of laminated plates

1.2 层合板三维运动学方程及本构方程

假设层合板振动时，第k子层空间上任意一点在x、y和ζ方向上的位移分别为uk，vk和wk，则该点的位移-应变方程为

(1)

式中：εkx，εky和εkζ为正应变分量；γkxy，γkxζ和γkyζ为切应变分量。

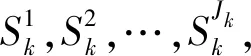
(2)

式中：Jk为计算面总数。

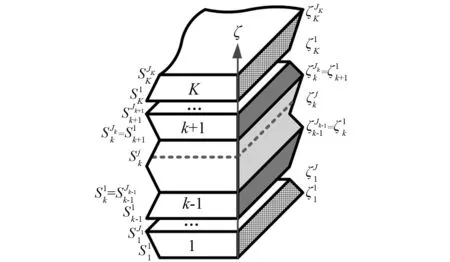
图2 层合板厚度方向上计算面分布情况Fig.2 Distribution of key surface in the transverse direction of alaminated plate

(3)

(4)

式中： 权重系数akjr为

(5)

令

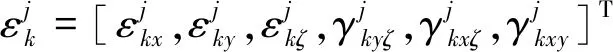
(6)

式中：σkx，σky和σkζ为正应力分量；τkxy，τkxζ和τkyζ为切应力分量。

因此，根据拉格朗日插值定理，第k铺层的整体位移及应变沿厚度方向分布情况可写为

(7)

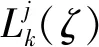
(8)

根据胡克定律，铺层k上任意点的应力分量可写为

(9)

式中：Ck为材料刚度系数矩阵，Tk为转换矩阵，具体表达式见文献[11-13]。

1.3 层合板振动能量泛函

层合板铺层k的应变能和动能方程可以写为

(10)

式中：ρk为材料密度，符号(·)表示对时间求导。结合式(10)和Hamilton原理即可推导出层合板第k铺层的3个振动控制微分方程。

对于由任意K层铺层复合而成的层合板，其振动问题涉及3K个控制微分程、6K-6个层间连续方程以及若干边界方程的联合求解。对于一般边界条件和铺层方式层合板，找到同时满足上述三类方程的解析解极其困难，通常需借助近似方法或数值解法进行求解。本文通过相邻两层共用层间计算面的方式来保证层间连续条件，同时采用Lagrange乘子和罚函数将边界约束方程转化为边界能量泛函的形式来满足一般边界条件求解需求。一般边界约束下子层的边界泛函可以写为

(11)

表1 不同边界条件下边界系数取值情况(x=xl边为例)Tab.1 Boundary coefficients for the classical boundaries of laminated plates (at the end of x=xl)

1.4 层合板振动特征方程

一般约束条件下，子层k的振动能量泛函可写为

Πktotal=Tk-Uks-Πkbc

(12)

(13)

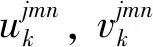
将式(10)、式(11)连同计算面位移分量的展开式代入式(12)，然后令泛函Πktotal对所有展开系数的变分为零，即

(14)

从而得到子层的振动特征方程为

(Kk-ω2Mk)Gk=0

(15)

式中：Kk和Mk分别为刚度和质量矩阵；Gk为待求系数向量。

最后，通过层间连续性条件将所有子层矩阵列式组装在一起即可得到层合板基于三维弹性理论的振动特征方程，组装方式如图2所示(质量矩阵和系数向量同理可得)。通过对整体矩阵方程进行特征值分解和数据后处理即可得到层合板固有频率和振型。

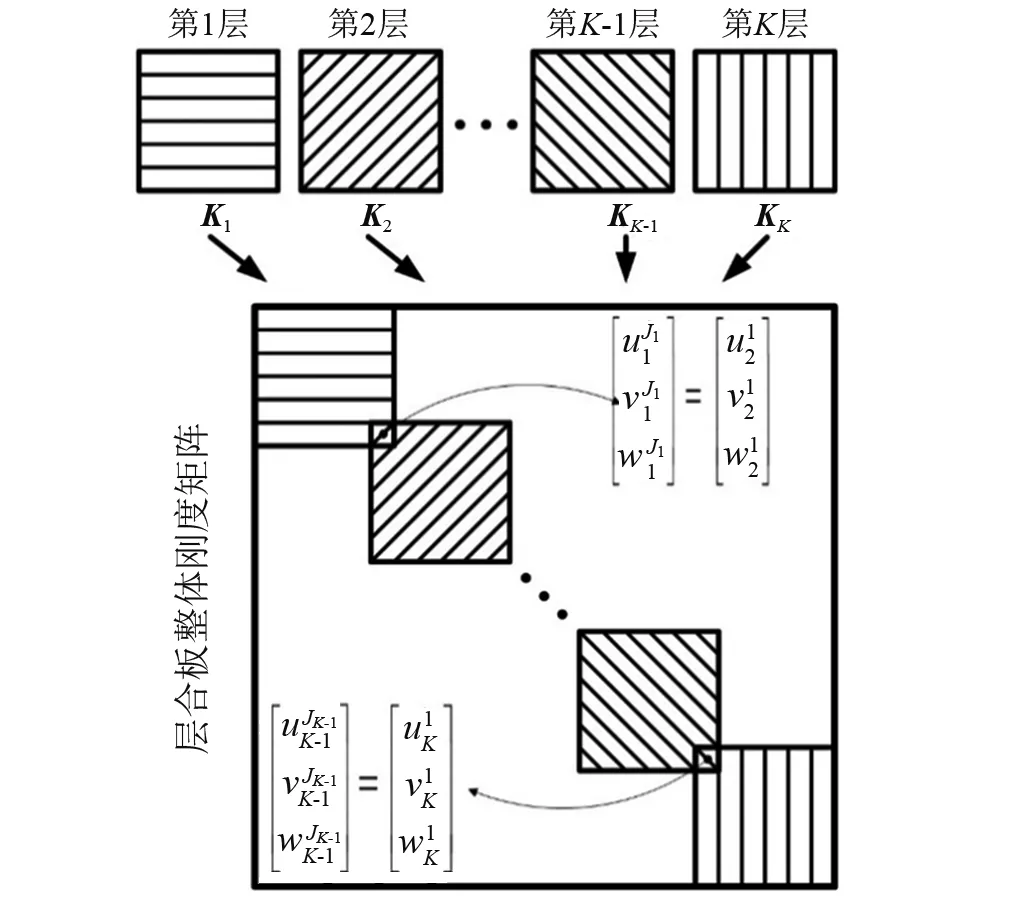
图3 层合板刚度矩阵组装方式Fig.3 Assemblage of the globalstiffness matrix

1.5 等效单层板理论解

常用的等效单层板理论主要有经典等效单层板理论(CPT)和一阶剪切变形等效单层板理论(FSDT)两大类。层合板基于CPT理论的位移场可表示为

(16)

式中：u0，v0和w0代表层合板中面各坐标方向上的位移分量。CPT理论位移形式简单，位移变量少，计算效率高，但忽略了横向剪切变形以及转动惯量的影响。

层合板基于FSDT理论的位移场可表示为

u(x,y,ζ,t)=u0(x,y,t)+ζφx(x,y,t),v(x,y,ζ,t)=v0(x,y,t)+ζφy(x,y,t),w(x,y,ζ,t)=w0(x,y,t)

(17)

式中：φx和φy分别为层合板横法线关于y轴和x轴的转角。FSDT舍弃了CPT理论中“结构变形后横法线仍然垂直于中曲面”的假设，从而克服了CPT理论不考虑结构横向剪切变形和转动惯量的先天缺陷，计算精度相对CPT理论有较大提高。但该理论本质上也一种等效单层理论，未能考虑横向伸缩变形的影响，且层间应力也不满足层间连续条件。此外，FSDT理论需引入剪切修正因子。本文算例中剪切修正因子取5/6。作者在文献[16]中借助改进傅里叶级数和Rayleigh-Ritz法建立了任意边界条件下层合板的基于等效单层板理论的振动特性求解方法，并验证了该方法的正确性，本文不再赘述。

2 层合板振动算例及分析

以不同边界条件和铺层方式下的层合板为研究对象，分析其振动特性，探究横向剪切和伸缩变形对层合板振动特性的影响。除非另有说明，层合板各铺层等厚且材料参数相同，为：E1=150 GPa，E2=E3=10 GPa，G12=G13=6 GPa，G23=5 GPa，ν12=ν13=ν23=0.25，ρ=1 450 kg/m3。为描述方便，以逆时针顺序对层合板的各边界条件进行标记。如，C-F-S-S表示板的x=x0，y=y0，x=x1和y=y1边的边界条件分别为固支，自由，简支，简支。

2.1 层合板自由振动特性

表2给出了[45°]复合厚板的前二十阶频率参数与有限元解(ANSYS, SOLID186单元，尺寸为0.05 m)的对比情况。复合板结构参数为：b=2 m，a/b=1，h/b=0.5。边界条件为F-F-F-F。可以看出，本文方法具有良好的收敛性质，计算量为“15-15-4”和“15-15-7”的两组解之间的误差不超过0.93%。此外，本方法结果与三维有限元解吻合良好。为了方便起见，下文算例中位移表达式的截断常数均取为M=N=15，并根据长宽比适当调整。

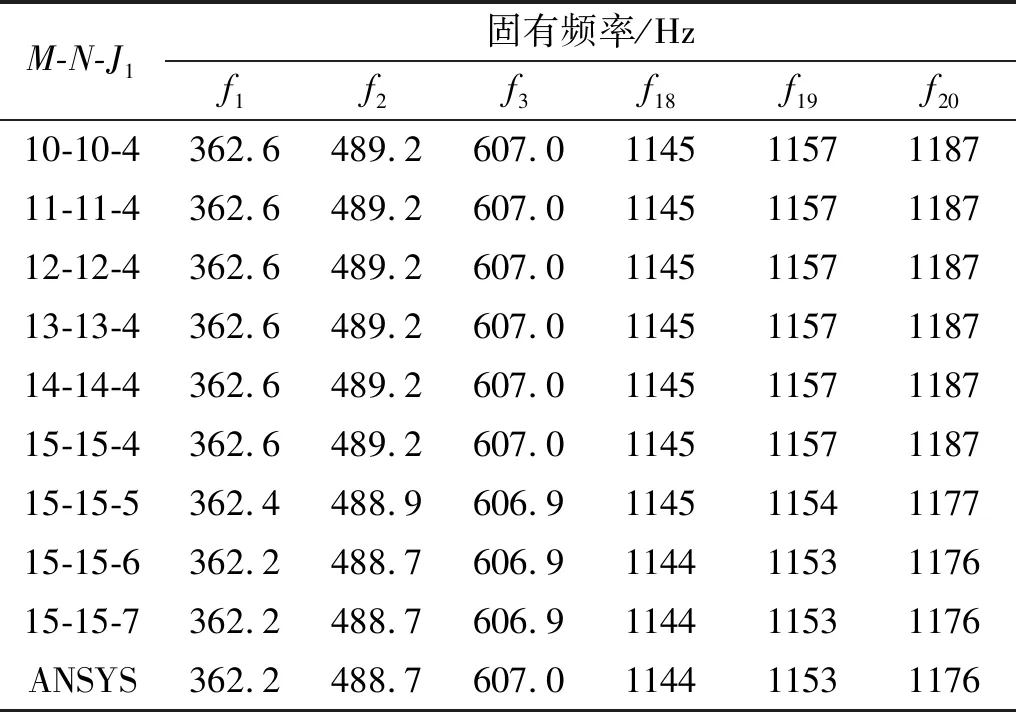
表2 四边自由[45°]复合厚板的前二十阶固有频率Tab.2 Natural frequencies for F-F-F-F [45°] composite plates

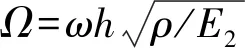
表3 [0/90°]2和[0/90°]4层合板无量纲基频Tab.3 The fundamental frequency parameters Ω of [0/90°]2和[0/90°]4 laminated plates

加时，其刚度与质量之比相应增加，根据ω2=k/m粗略估计，可知板的频率参数也将相应增加。当层合板厚度接近面内最小尺寸时，结构的各阶模态将发生变化，这一规律将不再适用。

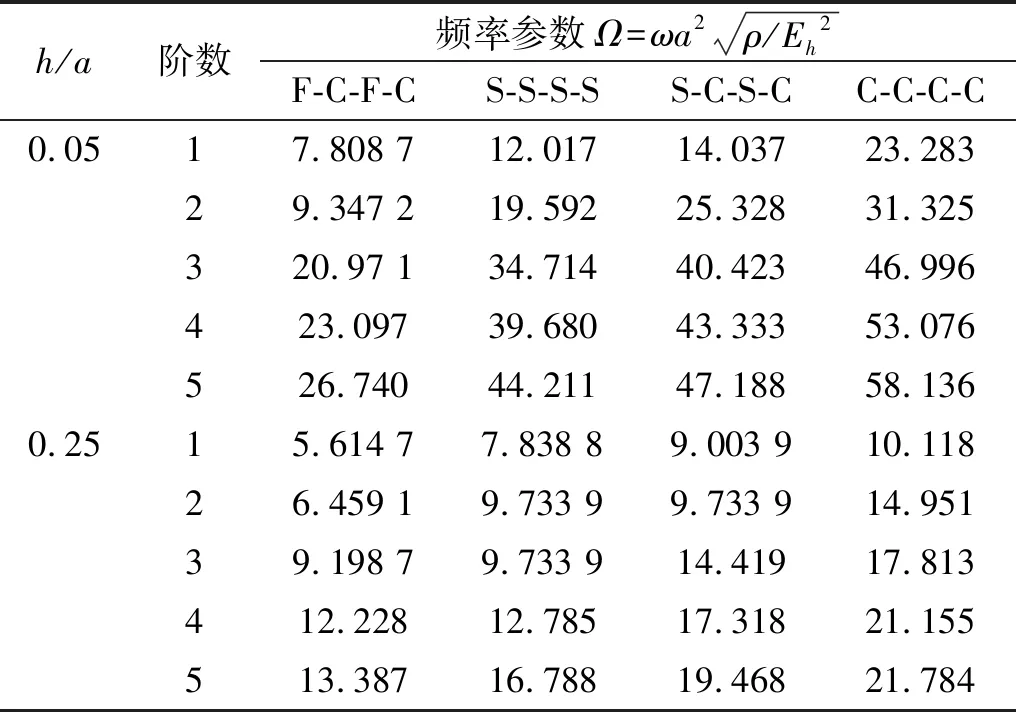
表4 不同厚度比下[0/90°/0]层合方板前五阶频率参数ΩTab.4 Frequency parameters Ω for[0/90°/0]layered plates of various thickness ratios

2.2 横向剪切及伸缩变形影响分析

以层合板三维弹性解为基准，系统对比不同边界条件、几何参数及铺层方式下基于等效单层理论的计算结果的偏差情况来探究横向剪切及伸缩变形对层合板振动特性的影响。偏差定义如下

偏差=(fCPT或FSDT-f3D)/f3D×100%

(18)

图4给出了不同边界条件下[0/90°/0]层合板基于CPT/FSDT两种理论的计算结果相对于三维弹性解的偏差随厚长比的变化情况。层合板的几何参数为：a=b=1。首先，可以看出，未考虑横向剪切变形的CPT理论的计算结果往往比考虑了横向剪切变形的FSDT理论的计算结果及三维弹性解大。其次，基于FSDT理论的计算结果和三维弹性解相差不大，这是因为本文所给出的是层合板的低阶模态频率，而层合板低阶模态以全局性的弯曲振动为主，因此横向伸缩影响并不大。此外，随着层合板厚度的增加，两种简化理论的偏差越来越大。这主要是由于经典理论忽略了剪切变形的影响，而在复合材料中，垂直于增强方向的杨氏模量一般不大，横向剪切变形较为明显。

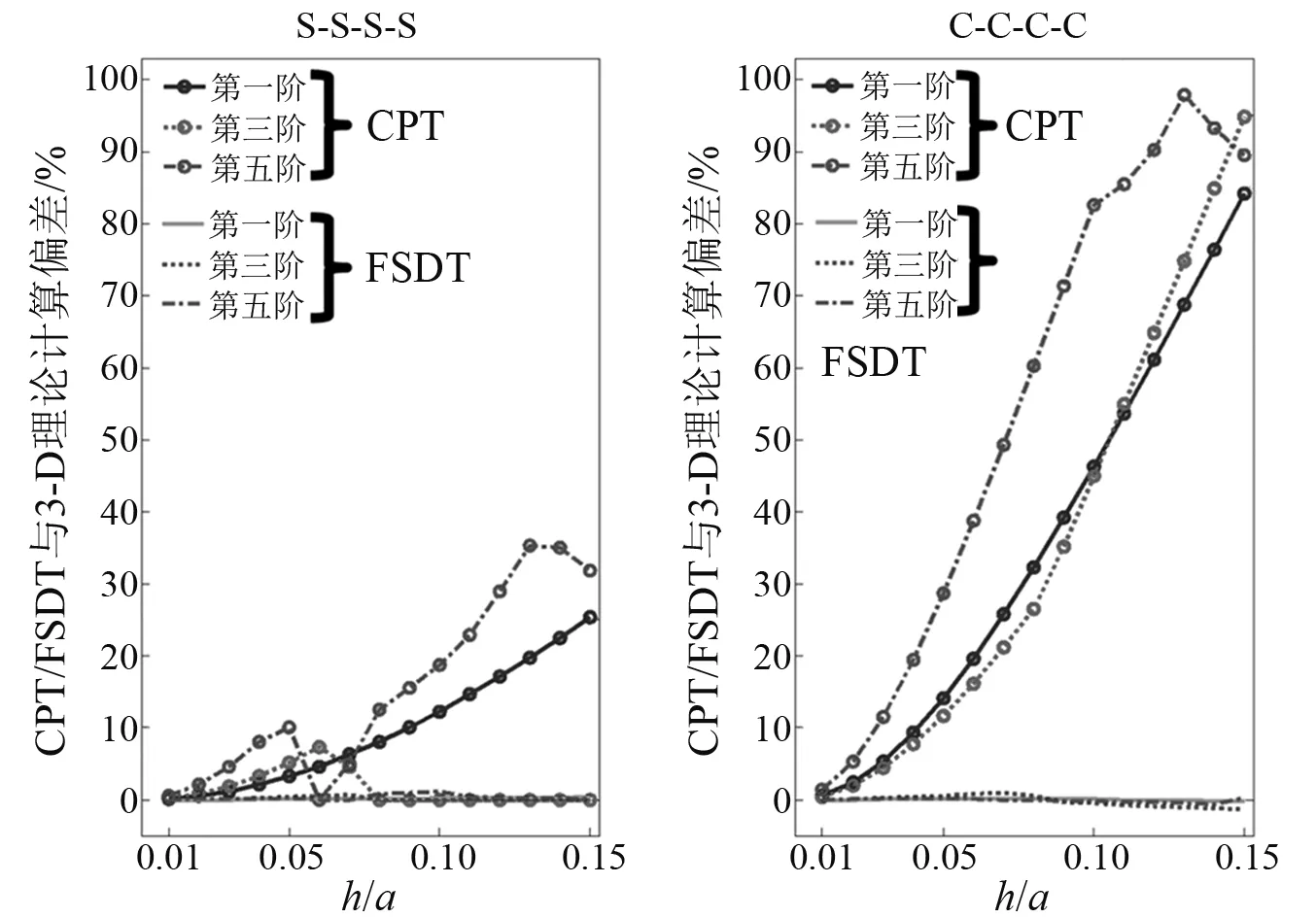
图4 不同边界条件下[0/90°/0]层合板基于CPT/FSDT 理论的计算结果相对于三维弹性解的偏差随厚长比的变化Fig.4 Deviation between frequencies obtained by the CPT/FSDT and the 3-D elasticity solution with respect to thickness ratio for [0/90°/0]laminated plates of various restraints

图5给出了四边固支[0/90°/0]层合方板基于FSDT理论的计算结果相对于三维弹性解的偏差情况。图中分别考虑了E1/E2=20和40两种情况。可以看出，E1与E2比值越大，层间材料性质差异越大，横向伸缩变形影响越大，层合板振动位移沿厚度方向锯齿分布现象越明显，FSDT理论解的偏差也越大。

图5 不同材料参数下四边固支[0/90°/0]层合板基于 FSDT理论的计算结果相对于三维弹性解的偏差情况Fig.5 Deviation between frequencies obtained by the FSDT and the 3-D elasticity solution for [0/90°/0] laminated plates of different anisotropy

图6给出了不同铺层方式下四边固支层合板基于CPT/FSDT两种理论的计算结果相对于三维弹性解的偏差随厚长比的变化情况。层合板的几何及材料参数与图4所用一致。可以看出，偏差曲线的变化趋势和前例一致，但不同铺层方式下，横向剪切变形对层合板振动频率的影响略有区别。总体来说，对基频的影响随厚度的增加而增加，而对于较高阶模态频率，由于结构内部弯曲、剪切和伸缩振动之间的耦合作用逐渐增强，偏差曲线略有波动。

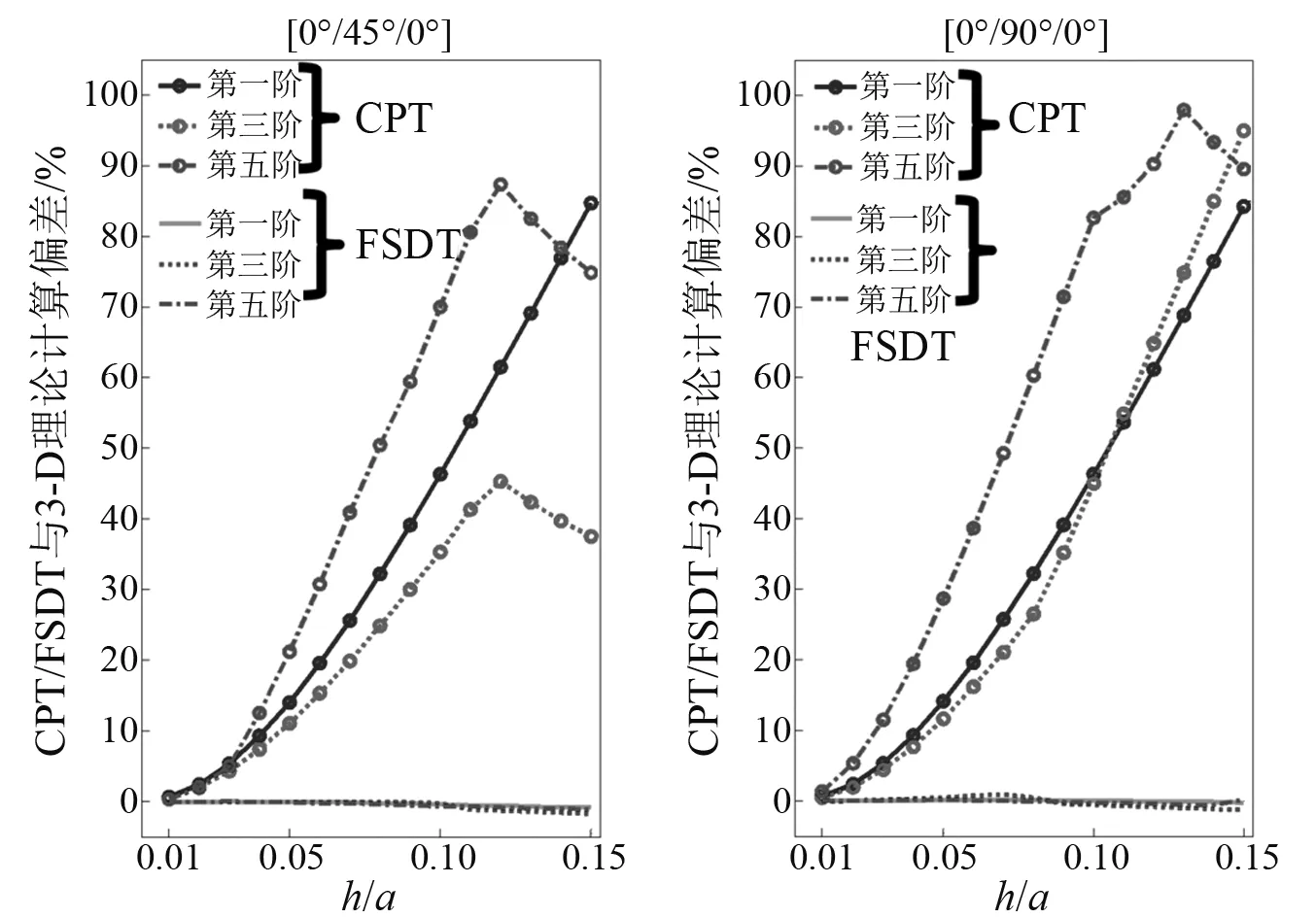
图6 不同铺层方式下四边固支层合板基于CPT/FSDT 理论的计算结果相对于三维弹性解的偏差随厚长比的变化Fig.6 Deviation between frequencies obtained by the CPT/FSDT and the 3-D theory with respect to thickness ratio for C-C-C-C laminated plates

图7给出了不同边界条件下[0/90°/软芯/0/90°]软芯夹层方板基于FSDT理论的计算结果相对于三维弹性解的偏差的随厚长比的变化情况。各子层材料参数[E1,E2,E3,ν12,ν13,ν23,G12,G13,G23,ρ]为：表层-[131 GPa, 10.34 GPa, 10.34 GPa, 0.22, 0.22, 0.49, 6.895 GPa, 6.205 GPa, 6.895 GPa, 1 627 kg/m3]，芯体-[6.89 MPa, 6.89 MPa, 6.89 MPa, 0, 0, 0, 3.45 MPa, 3.45 MPa, 3.45 MPa, 97 kg/m3]。表层和芯体的厚度为h0°∶h90°∶hcore∶h0°∶h90°=1∶1∶20∶1∶1。可以看出，基于FSDT理论的计算结果远远高于三维弹性解，而且随着厚长比增加，这一差异越来越明显。即使是厚长比为0.05的情况下，最大偏差达到了700%以上。这是由于软芯和表层材料性质差异较大，层间锯齿效应也越明显，而FSDT假设的连续线性模型严重不符合实际情况，偏差较大。

图7 不同边界条件下[0/90°/软芯/0/90°]夹层方板 基于FSDT理论解相对于三维弹性解的偏差随厚长比的变化Fig.7 Deviation between frequencies obtained by the FSDT and the 3-Dtheorywith respect to thickness ratio for[0/90°/soft-core/0/90°]sandwich plates

图8给出了S-S-S-S边界条件下[0/90°/0]和[0/90°]层合方板基于FSDT理论的计算结果相对于三维弹性解的偏差情况。各子层材料参数与图7算例表层材料参数一致。可以看出，于对称铺设层合板相比，横向伸缩变形对非对称铺设层合板的影响更大。

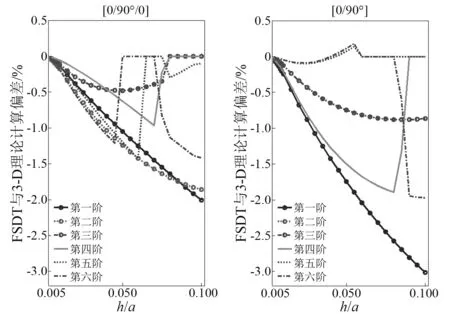
图8 不同边界条件下[0/90°/软芯/0/90°]夹层方板 基于FSDT理论解相对于三维弹性解的偏差随厚长比的变化Fig.8 Deviation between frequencies obtained by the FSDT and the 3-Dtheorywith respect to thickness ratio for[0/90°/soft-core/0/90°]sandwich plates

图9给出了表层与芯层厚度比变化时四边固支[0/软芯/0]夹层方板基于FSDT理论的计算结果相对于三维弹性解的偏差随厚长比的变化情况。夹层板的各子层材料参数与图7所用一致。可以看出，随着软芯层厚度占比的降低，FSDT与三维弹性理论之间的偏差降低。这是由于软芯层厚度方向上杨氏模量较小，横向伸缩变形较为显著，而当其厚度减小时，弯曲振动逐渐主导层合板的低频模态，横向伸缩变形的影响逐渐降低，因此未考虑横向伸缩变形影响的FSDT理论与三维弹性理论之间的差异也逐渐降低。

图10给出了芯层材料参数变化时四边固支[0/软芯/0]三明治方板基于FSDT理论的计算结果相对于三维弹性理论计算结果的偏差随厚长比的变化情况。除了芯层杨氏模量外，三明治板表层和芯层的其他材料参数与图7所用一致，表层和芯层厚度比为hface∶hcore∶hface=1∶1∶1。可以看出，随着软芯材料参数与表层材料参数差异性减小，FSDT理论相对于三维弹性理论的偏差越来越小。这是由于软芯层材料参数越接近于表层时，层间位移的锯齿效应越不明显，三明治板越接近各向同性均质结构，从而假设位移沿厚度方向线性分布的FSDT理论相对于三维弹性理论的偏差也逐渐减小。

图4～10中还可以看出偏差曲线出现跳跃现象。这是因为随着厚度增加，结构的振动从以弯曲变形为主的振动模态逐渐过渡到弯曲、伸缩、扭转、剪切变形共同主导的振动模态，振动模态越来越复杂，横向剪切及伸缩变形的影响也越来越复杂。当厚度大到一定程度，结构可能从以弯曲变形为主的模态切换到剪切变形为主的模态或者其他变形主导的振动模态。针对不同模态，横向剪切及伸缩变形的影响不尽相同，因此图中曲线出现跳跃。

图9 四边固支[0/软芯/0]夹层方板基于FSDT理论的 计算结果相对于三维弹性解的偏差随厚长比的变化Fig.9 Deviation between natural frequencies obtained by the FSDT and the 3-D theory with respect to thickness ratio for [0/soft-core/0]sandwich plates of C-C-C-C restraint

图10 芯层材料参数变化时四边固支[0/软芯/0]夹层 方板基于FSDT理论的计算结果与三维弹性解的偏差情况Fig.10 Deviation between natural frequencies obtained by the FSDT and the 3-D theorywith respect to thickness ratio for[0/soft-core/0]sandwich plates of C-C-C-C restraint

3 结 论

本文基于广义谱方法和微分求积法建立了一种适用一般边界条件和铺层方式的层合板振动三维解法，并验证了方法的收敛性和计算精度。系统分析了不同边界条件和铺层方式下横向剪切及伸缩变形对层合板振动特性的影响。研究结果表明：

(1) 横向剪切变形对层合板固有频率的影响非常显著。总体来说，对基频的影响随厚度的增加而增加，而对于较高阶模态频率，由于结构内部弯曲、剪切和伸缩振动之间的耦合作用逐渐增强，难以定量或者定性估计。

(2) 横向伸缩变形对各铺层材料参数相同的层合板的固有频率影响不大，而对于各铺层材料性质差异明显的层合板，其影响非常显著，且随厚度比增加而加剧，如在软芯夹层方板计算中，忽略横向伸缩变形的计算偏差达到了700%以上。

(3) 层合板各铺层材料差异度越小，层间锯齿效应越不明显，基于连续位移假设的等效单层理论相对于三维弹性理论的偏差也越小。