EDRS在滚动轴承振动信号盲源分离中的应用
刘鲲鹏, 夏均忠, 白云川, 吕麒鹏, 郑建波
(陆军军事交通学院 军用车辆工程系,天津 300161)
滚动轴承故障诊断是机械工程领域的热点问题,通常采用振动分析法进行研究[1-3],然而实际采集到的轴承信号成分复杂,无法直接进行有效的故障诊断。盲源分离作为信号处理的重要环节,可在信号的理论模型和源信号无法获知的情况下,从混叠信号中分离出较为单纯的源信号,具有一定的应用价值[4]。
确定性随机分离(Deterministic Random Separation, DRS)是Antoni提出的一种盲源分离方法,该方法以同步平均技术为核心,通过提取信号中的确定性成分实现混叠信号的分离,恢复各个源信号的状态[5-7]。然而DRS本身只适用于分离稳速状态下的信号,且在变转速工况下,振动信号的幅值波动较为剧烈[8-9],在DRS算法中也未提及相应对策。因此,变转速下振动信号盲源分离问题亟待解决。
为实现变转速下滚动轴承振动信号盲源分离,论文在DRS方法的基础上提出扩展确定性随机分离(Extended Deterministic Random Separation, EDRS)方法。首先应用角域重采样技术减少转速变化的影响,然后借助Z计分模型降低信号幅值波动,最后提取变转速信号的确定性成分,同时得到信号随机成分。通过仿真分析和轴承试验证明EDRS的有效性,并对其应用价值进行分析。
1 确定性随机分离(DRS)
根据信号实际变化规律,可将其分为确定性信号和随机信号。所谓确定性信号,即能够用明确的数学关系表示的信号,其波形可描述为某个特定的时间函数;确定性信号又可分为周期确定性信号和非周期确定性信号。随机信号的波形无法表示为具体的函数形式,仅能通过统计学方法对其特性进行描述;随机信号又可分为平稳随机信号和非平稳随机信号[10]。滚动轴承工作时产生的振动信号是一种多成分混叠的随机信号,根据振动信号的形成机理可知变转速下滚动轴承振动信号主要包含以下三种成分[11]:
(1) 轴承故障冲击序列(平稳随机成分);
(2) 转频振动及其谐波(确定性成分);
(3) 随机噪声(非平稳随机成分)。
由于多种信号成分之间相互影响,使得变转速下的故障冲击难以识别,因此在进行诊断之前,需要先对信号进行预处理。
DRS与大多数振动信号预处理方法不同,它并没有通过一般意义上的降噪处理突出故障脉冲,而是从恢复源信号的角度出发,提取出较为单纯的信号成分,得到所需要的信号特征。在对滚动轴承振动信号进行处理时,通常运用同步平均技术提取其中的周期确定性成分,将背景噪声留在随机成分中,实现信号的盲源分离。确定性随机分离(DRS)的原理如下:
对于回转频率为f0的振动信号x(t), 假设信号采样的时间间隔为Δt, 则Δt对应的离散信号为x(nΔt), 记为x(n)。 由于稳速时任意两个转速脉冲间隔的采样点数相同,因此可记为M, 以M作为子信号数组的大小将x(n)分为p段,则同步平均算法公式为
(1)
对式(1)进行Z变换并化简,可得同步平均系统的幅频特性为[12]
(2)
式中:f为响应频率;A(f)为响应频率对应的幅值。
假设信号x(n)由周期确定性成分D(n)和随机成分R(n)组成,则有
x(n)=D(n)+R(n)
(3)
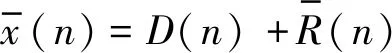
(4)
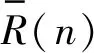
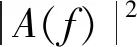
(5)
以一个频域周期为例,同步平均前后信号中随机成分的功率之比为
(6)
结合式(2),化简可得
(7)
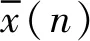
需要指出的是,p的取值并不是越大越好。虽然p值的增大会加强对信号随机成分的抑制作用,但同时也会增加同步平均计算过程中产生的相位误差累积效应,降低信号确定性成分的幅值增益,导致分离效果适得其反。因此在实际应用时,应当综合考虑有用信号的幅值增益和无关信号的衰减程度,科学确定平均段数,以达到最佳的分离效果[13]。
2 扩展确定性随机分离(EDRS)
DRS借助同步平均技术实现了稳速状态下滚动轴承振动信号盲源分离,但无法有效分离变转速工况下的轴承信号,同时未考虑信号幅值波动问题,导致其应用范围受到较大限制。论文基于以上两点提出扩展确定性分离(EDRS)方法:首先应用角域重采样技术将时域变转速信号转化为角域稳态信号,其次借助经济学领域Z计分模型对上述信号进行归一化处理,降低变转速下滚动轴承振动信号幅值波动,最后建立轴承信号确定性成分提取函数,实现变转速下滚动轴承振动信号盲源分离。
2.1 Z计分模型
Z计分模型是一种多变量经济评估模型,在金融风险预测中得到了有效应用[14]。它提出了Z值(判别函数值)的概念并给出了其正常的变化范围,具体计算公式如下
Z=1.2X1+1.4X2+3.3X3+0.6X4+99.9X5
(8)
式中:Xi为各类经济学统计量;Z为判别函数值。
在Z计分模型中,由于计算Z值所需变量的单位不一致,且数值水平往往相差较大,因此在计算之前需要对数据进行无量纲归一化处理。针对不同的数据类型和实际情况,Z计分模型中使用的数据归一化具体方法有所不同,但都是为了最大限度消除数据间的差异,实现Z值在各类计算状况下的动态统一。
对于变转速下滚动轴承振动信号,转速变化会加剧信号幅值的异常波动,导致采集到的信号数值水平差异较大,这是影响变转速下振动信号分析效果的重要因素。因此借助Z计分模型中数据归一化的思想,对变转速下滚动轴承振动信号进行归一化处理。
2.2 EDRS原理
对于转速随时间变化的滚动轴承振动信号y(t),其角速度可表示为
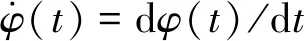
(9)
式中:φ(t)为时间t对应的角位置。此外,对于载荷也随时间变化的情况,其载荷用l(t)表示。
首先在角域对原始时域信号进行重采样,转化过程如下
y′(φ)=y(φ(t))
(10)
式中:y′(φ)即为信号y(t)在角域的表示。
其次根据Z计分模型中数据归一化的思想,对重采样后的信号做如下归一化处理
z(φ)=y′(φ)/g′fl(φ)
(11)
式中:g′fl(φ)为y′(φ)的低通滤波包络值,计算方法如下
g′fl(φ)=gfl(φ(t))
(12)
式中:gfl(t)为对y(t)的包络值进行低通滤波的结果,fl为低通滤波截止频率,计算方法如下
(13)
(14)
(15)
最后从归一化处理后的信号中提取角域确定性成分,步骤如下:
(1) 对z(φ)进行短时傅里叶变换
(16)
式中:Z(Θ,Ψ)代表对z(φ)进行短时傅里叶变换的结果;w(φ)代表非零窗函数;Ψ为角位移;Θ为角频率。
(2) 建立用于提取角域信号确定性成分的传递函数,其关系式如下
(17)
式中: 〈·〉Ψ代表沿Ψ的平均运算; *代表共轭复数;Φ为角周期;G(Θ)为角域信号的确定性成分。
得到信号的角域确定性成分后,将其反向转回时域,与原始时域信号进行对比,二者之差即为轴承振动信号的随机成分。
EDRS算法流程如图1所示。
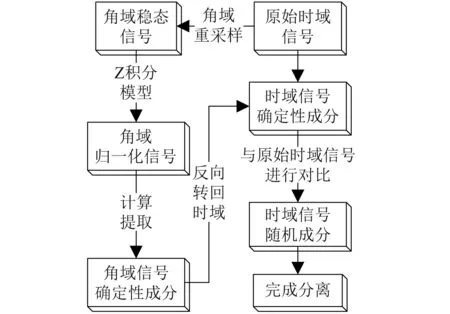
图1 EDRS算法流程Fig.1 The algorithm flow of EDRS
3 仿真分析
为了从理论上分析EDRS的有效性,设计滚动轴承变速仿真信号进行验证。假设轴承内圈回转,外圈固定,变转速轴承故障振动信号仿真模型如下
(18)
式中: 第一部分为轴承故障引起的冲击序列, 其中Ai为第i次冲击的幅值,Ti为第i次冲击发生的时刻; 第二部分为转频振动及其谐波,其中Bm和βm分别为m次谐波的幅值和初始相位,f(t)为轴承的瞬时转频;第三部分为随机噪声。
冲击序列s(t)用指数衰减的正弦信号来模拟。
s(t)=e-αtsin(2πfrt)
(19)
式中:α为冲击信号的阻尼比,取500;fr为轴承的共振频率,取2 000 Hz。
假设振动信号中共包含转频的3个谐波分量,其幅值和相位分别为:B1=0.3,B2=0.5,B3=0.4,β1=π/6,β2=-π/3,β3=π/2; 轴承转频由公式(20)给出
f(t)=2.5t+5
(20)
添加白噪声,信噪比为-2 dB。
信号采样频率为10 kHz,采样时间为4 s。变转速滚动轴承故障仿真信号时域波形如图2所示。其中图2(a)为加速条件下的故障冲击序列,由于转频随时间不断增加,冲击序列变得越来越密集,冲击幅值也在相应增加;图2(b)表示转频振动及其谐波,从中可以明显看出其周期确定性特征;图2(c)为(a)与(b)叠加的结果,此时的信号不含随机噪声;图2(d)表示加噪后变转速轴承故障仿真信号。
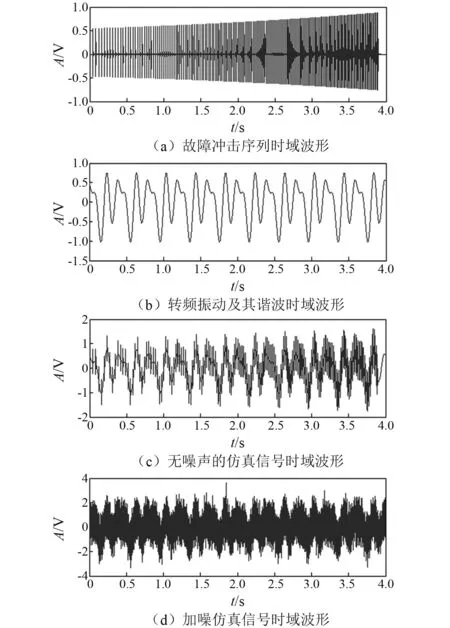
图2 变转速滚动轴承故障仿真信号时域波形Fig.2 The time domain waveform of bearing simulation signal in variable speed
应用EDRS对仿真信号进行处理,信号被分离为两部分,如图3所示。图3(a)表示的信号成分与原始转频振动及其谐波的时域波形(图2(b))基本吻合;随机信号功率为信号总功率的0.69%,该信号几乎均为确定性成分。图3(b)表示除确定性成分以外的随机成分,主要包括故障冲击序列和随机噪声。结果表明,EDRS能够将变转速信号分离为确定性成分和随机成分。
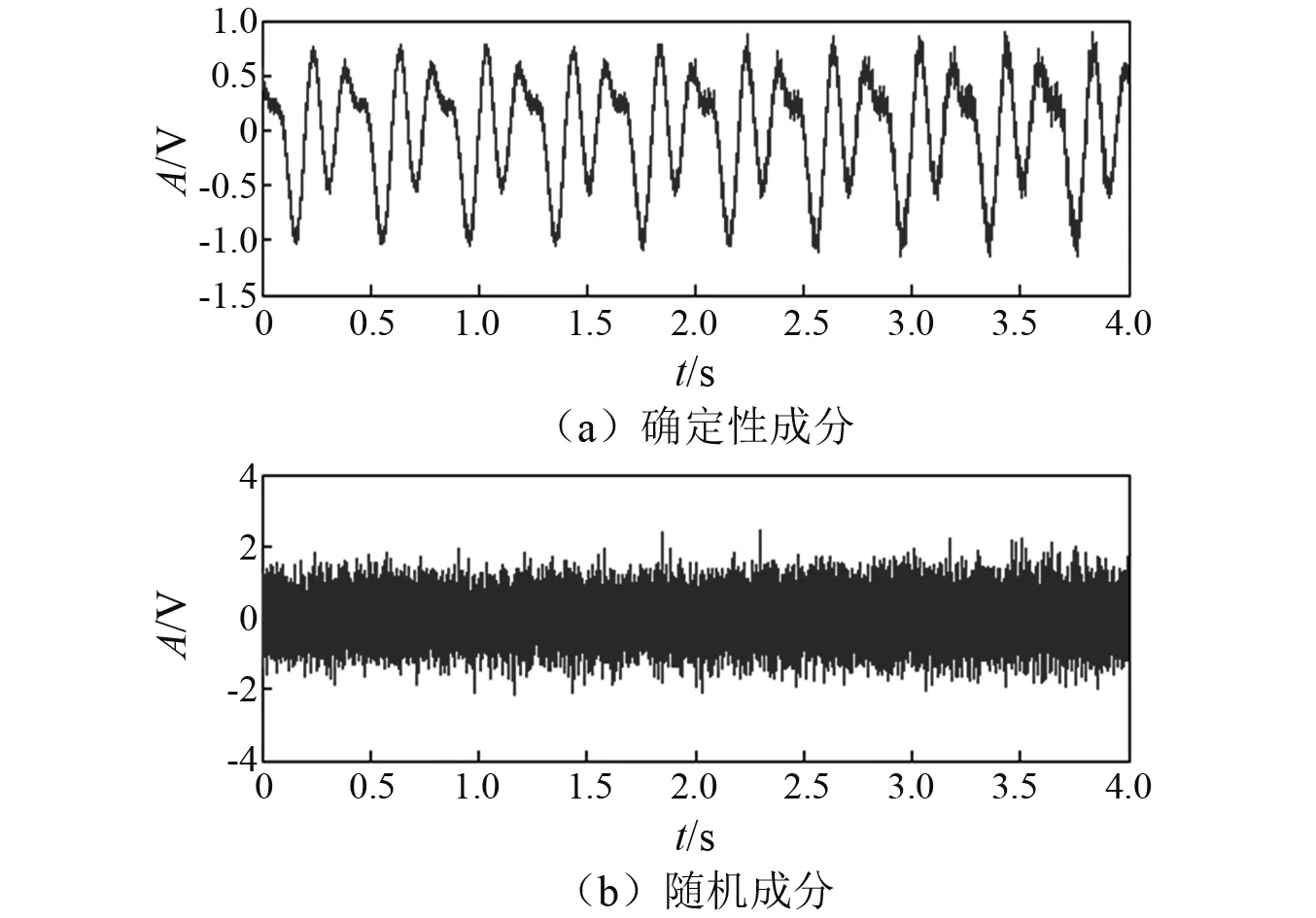
图3 EDRS分离仿真信号结果Fig.3 EDRS separation results of simulation signal
4 试验验证
试验装置由驱动电机、转速传感器、连接轴、联轴器、试验轴承和振动加速度传感器等组成,如图4所示[15]。选取Polytec激光测振仪获取转速信号,使用Briiel & Kjaer4397加速度计采集振动信号。
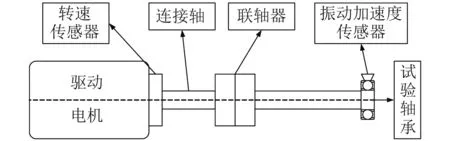
图4 试验装置Fig.4 Test device
试验所用MB-ER-16K 1型轴承安装在连接轴远离电机的一端,其技术参数见表1。在轴承外圈上加工直径为3 mm,深度为1 mm的圆坑,用于模拟点蚀故障。

表1 MB-ER-16K 1型轴承参数Tab.1 Parameters of MB-ER-16K 1 bearing
根据滚动轴承技术参数,计算得到外圈故障特征阶次理论值为
电机转速保持在10~15 Hz之间变化,采样频率为50 kHz,采样时间为21 s。采集滚动轴承外圈故障振动信号,得到其转速变化情况及振动信号时域波形,如图5所示。

图5 轴承转速曲线及其外圈故障振动信号时域波形Fig.5 Bearing speed curve and the time-domain waveform of outer race fault vibration signal
4.1 分离效果分析
应用EDRS方法对信号进行盲源分离,得到确定性成分和随机成分,如图6所示。为进一步分析两种信号成分的特性,引入样本熵对其进行评价[16]。分别计算原始信号、确定性成分(图6(a))和随机成分(图6(b))的样本熵值,结果见表2。原始信号的样本熵值略高于确定性成分,但明显低于随机成分。EDRS能够有效实现变转速下故障轴承振动信号盲源分离。
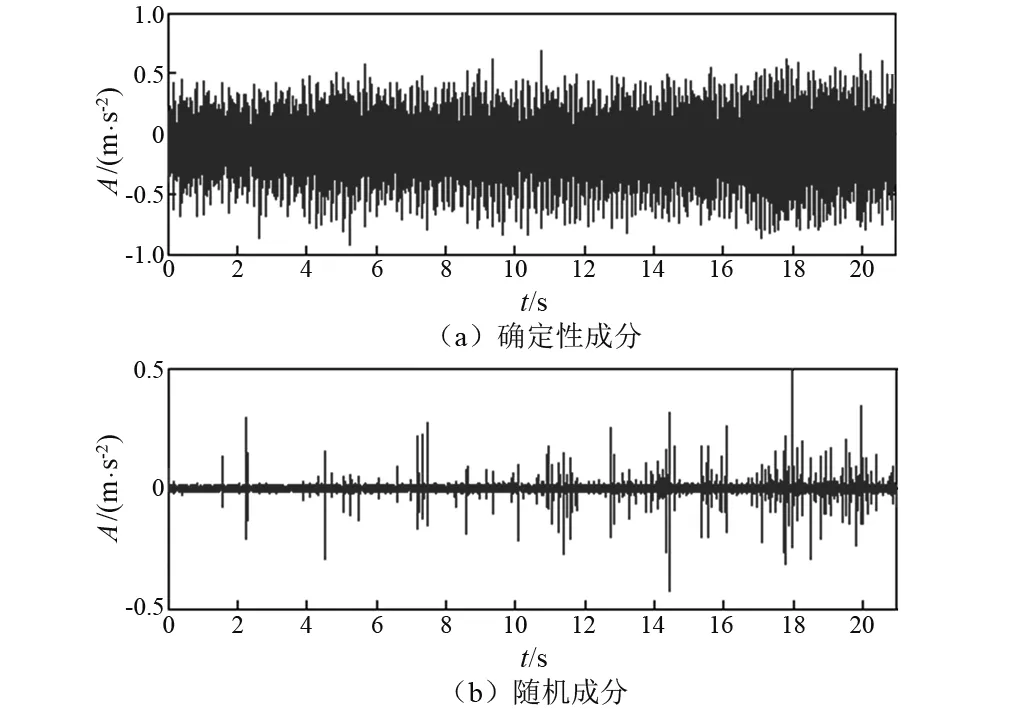
图6 EDRS方法分离结果Fig.6 The separation resultfrom EDRS method

信号类型原始信号确定性成分随机成分样本熵值0.238 60.085 32.022 4
4.2 应用价值分析
应用循环平稳理论中阶频谱相关(Order-frequency Spectral Correlation, OFSC)分别提取信号随机成分及原始信号的特征[17-18],结果如图7所示。图7(a)为信号随机成分的提取结果,从中可明显识别故障特征阶次3.590及其二倍、三倍阶次,与滚动轴承外圈故障特征阶次的理论值(3.592)及其二倍、三倍阶次基本一致,故障特征与实际故障类型相吻合。
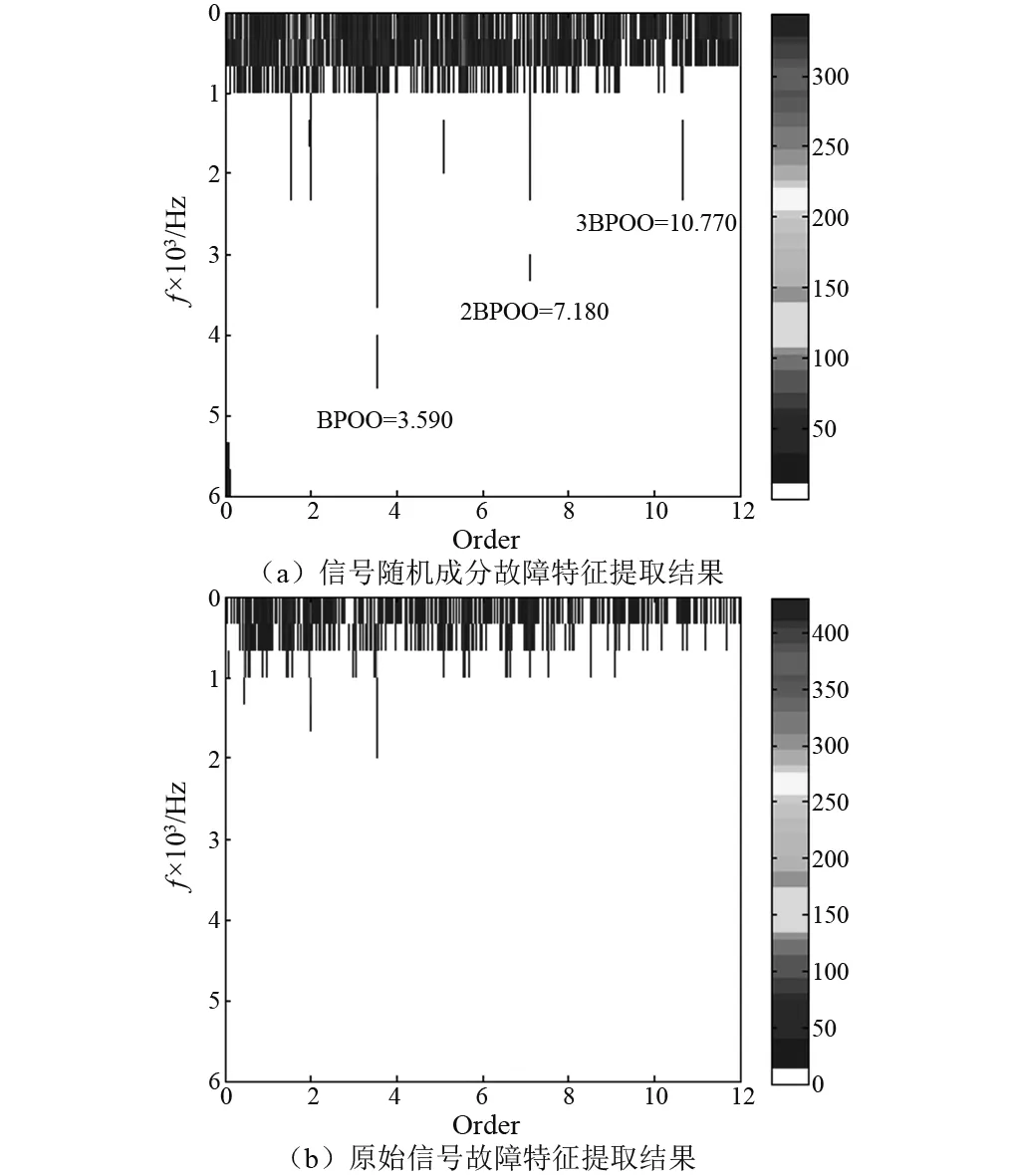
图7 信号随机成分及原始信号故障特征提取结果Fig.7 The fault feature extractionresultof signal random components and original signal
图7(b)为原始信号的提取结果,从中无法判断故障特征阶次,这是由于原始信号成分相对复杂,导致OFSC的计算效果受到较大影响。EDRS将原始信号分离为两种相对单纯的成分,且随机成分包含的故障冲击更加明显,从中能够有效提取轴承故障特征。因此EDRS能够优化变转速下滚动轴承故障特征提取效果,具有实际应用价值。
4.3 与传统方法的对比
独立分量分析(Independent Component Analysis, ICA)是研究信号盲源分离的常用方法,在解决独立统计源信号分离问题时取得了良好效果[19]。应用ICA分离图5(b)信号,结果如图8所示。计算其信号成分的样本熵,结果见表3。通过ICA得到的图8(a)信号成分、图8(b)信号成分和原始信号的样本熵值无明显差异,说明ICA未能有效分离原始信号。
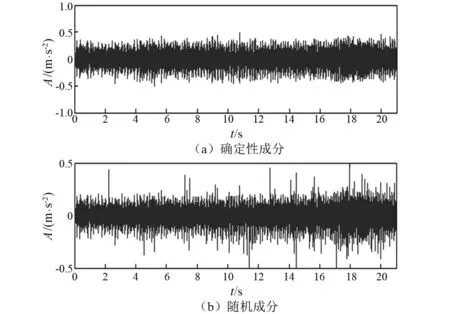
图8 ICA方法分离结果Fig.8 The separation resultfrom ICA method

信号类型原始信号图8(a)信号成分图8(b)信号成分样本熵值0.238 60.127 50.653 2
应用阶频谱相关对ICA分离出的随机成分(图8(b))进行处理,结果如图9所示,信号中其它无关阶次
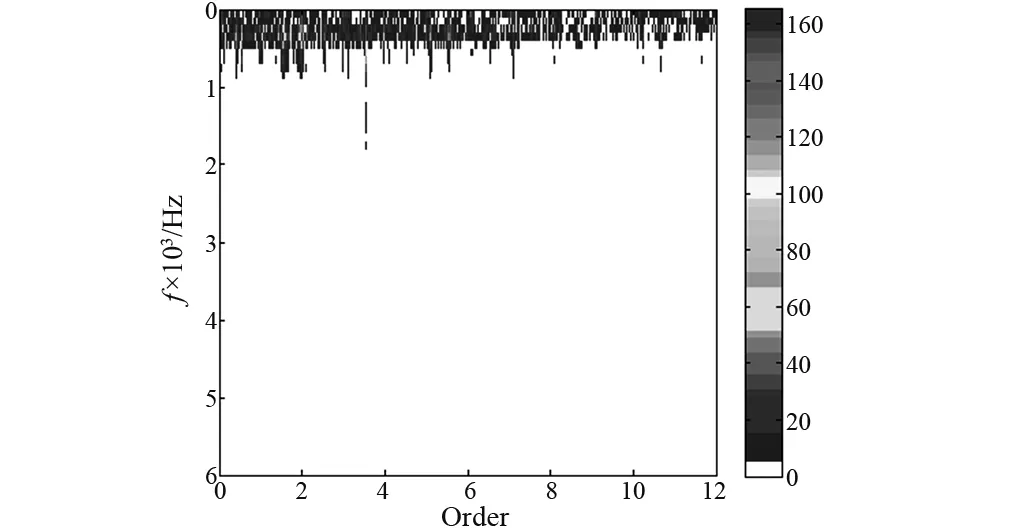
图9 ICA分离后信号随机成分故障特征提取结果Fig.9 The fault feature extraction result of signal random component after separation by ICA
受到了一定程度的抑制,但无法识别出故障特征阶次,主要原因在于ICA没有考虑轴承转速变化和信号幅值波动的影响,导致信号分离效果不佳。
5 结 论
论文深入研究了确定性随机分离(DRS)的原理,在此基础上提出了一种变转速下振动信号盲源分离方法——扩展确定性随机分离(EDRS),并通过仿真分析和轴承故障试验证明了该方法能够将变转速信号分离为确定性成分和随机成分。
(1) 结合角域重采样技术和Z计分模型可将经典的DRS方法改进为扩展确定性随机分离(EDRS)方法,实现变转速下滚动轴承振动信号的盲源分离。
(2) EDRS能够将原始信号分离为两种相对简单的成分(确定性成分和随机成分),优化变转速下滚动轴承故障特征提取效果,具有实际应用价值。
(3) 与传统的独立分量分析(ICA)相比,EDRS综合考虑了轴承转速变化和信号幅值波动的影响,性能更加优越,能够有效完成变转速信号盲源分离。

