基于分时段规范变量残差分析的高速自动机动态特性监测

王宝祥， 潘宏侠

(1. 中北大学 机械工程学院，太原，0300512. 淮阴工学院 机械与材料工程学院，江苏 淮安 223003)

高速自动机是自动武器系统的核心部件，主要由枪机框、供弹机、闭锁机构、击发机构等组成。枪弹击发时，在膛内高压气体剧烈冲击作用下，高速自动机各个部件在极短的时间内需要经历复杂的形态转换过程，关键构件发生的变形、裂纹乃至失效，将直接影响到整个武器系统的可靠性和可用性。高速自动机故障分类研究使用故障样本训练分类器[1-3]，但现实中枪械的故障样本很难收集。为确保战时发挥武器系统最佳性能，对其开展早期故障监测研究更具有现实意义。

故障诊断分类器需要较大规模的故障样本保证识别精度[4-5]。多变量统计过程控制方法仅以健康系统的状态数据建立参考模型，通过度量未知状态数据与参考模型的偏差来监测系统的运行状态，在将来的工程应用中更容易实施。Yu[6]采用局部保持投影(Locality Preserving Projections, LPP)开展滚动轴承性能退化评估研究，成功检测到轴承早期退化趋势；Lu等[7]采用主成分分析(Principal Component Analysis, PCA)融合多域特征来描述回转支承的退化轨迹。考虑到机械系统早期故障信息常被强背景噪声所淹没，Žvokelj等[8]提出一种基于集成经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)和独立成分分析(Independent Component Analysis, ICA)的回转支承状态监测方法，该方法利用EEMD将原始信号的频谱按照由高频到低频顺序展开，对每个频段建立ICA模型来检测回转支承的微弱故障特征。然而，上述多变量统计分析方法由于没有考虑时间序列中的相关性，无法反映机械系统的动态特性。为此，Yu[9]提出一种动态局部和非局部保持投影(Dynamic Local and Nonlocal Preserving Projection, DLNPP)来监测随时间动态变化的轴承运转状态。Wu等[10]利用动态主成分分析(Dynamic PCA, DPCA)结合马氏距离(Mahalanobis Distance, MD)来揭示滚动轴承退化过程的动态特性。规范变量分析(Canonical Variate Analysis, CVA)定义于由规范变量形成的状态空间，其通过寻找一种线性组合使两组变量间的相关性达到最大，比传统的PCA方法更适用于动态系统的状态监测[11]。后来，Pilario等[12]计算了未来观测数据与过去观测数据的规范变量的残差，提出一种规范变量残差分析方法(Canonical Variate Dissimilarity Analysis，CVDA)，实验表明残差信号对动态系统的早期故障特征更加敏感。

高速自动机的运动形态具有多行程特点，在故障萌芽时期，构件的异常状态信息十分微弱，且与强背景噪声相互混叠，早期故障特征很难被提取和识别。为开展高速自动机的动态特性监测，及时发现关键部件微弱的故障冲击特征，首先针对高速自动机的往复运动特性，对短时瞬态冲击信号进行时段划分，然后以正弦辅助经验模态分解(Sinusoid-assisted Empirical Mode Decomposition, SEMD)将短时瞬态冲击信号分解、重构为高频和低频成分，接着以规范变量残差分析方法建立高速自动机的动态特性监测模型，形成一种分段式规范变量残差分析方法(Phase-Partitioned CVDA, PCVDA)。最后通过对某12.7 mm高射机枪的动态特性进行监测，验证了该方法的有效性。

1 SEMD

SEMD自适应地构造常规正弦辅助函数来分离信号的固有模态，保留了传统经验模态分解方法的自适应性。该方法通过以下三个方面抑制模态混叠：①在信号分解过程中迭代产生不同的正弦辅助函数；②根据嵌入信号的固有模态自适应的构造正弦辅助函数；③通过相位平移改变模态函数极值点的位置，保留更多固有模态信息。

正弦辅助信号可表示为

sk(t|ak,fk,θk)=akcos(2πfkt+θk)

(1)

式中：k为第k次分解；ak,fk和θk分别为信号幅值、频率和相位；θk控制极值点的相对位置。SEMD分解任意时间序列x(t)的步骤如下[13]：

步骤1确定正弦辅助函数sk(t|ak,fk,θk)。对x(t)进行经验模态分解(Empirical Mode Decomposition, EMD)，根据固有模态函数(Intrinsic Mode Functions, IMF)确定正弦辅助函数的幅值ak和频率fk，θki按相位平移量I(1≤i≤I)在[0, 2π]内按均匀抽样确定。

步骤2EMD从新信号x(t)+sk(t|ak,fk,θk)中分离出第一个振荡模态IMF1，将I个IMF1的平均定义为目标振荡模态ck(t)。

步骤3从分析信号x(t)中减去ck(t)

x(t)=x(t)-ck(t)

步骤4重复“步骤1至步骤3”直到分离出所有振荡模态IMF，将剩余成分记为残差rn(t)。

SEMD认为如果存在模态混叠问题，则一个IMF中不止有一个固有模态，该方法通过寻找目标模态自适应地设计正弦函数sk。若以EMD的分解结果cik′(t)(1≤k′≤K′)作为初始模态，cik′(t)由高频到低频顺序排列，目标模态则定义为ci1(t)中的最高频成分。若ci1(t)中两个模态的频率满足

f1/f2>1.5或f2/f1<0.67,f1>f2

(2)

则两个模态是可分离的。SEMD首先对极值点(其瞬时频率和幅值分别为fi1(e)和ai1(t)， 其中e表示极值点序号。)的瞬时频率进行层次聚类分析，将初始类数设为P=K′，并迭代减少聚类数量P=P-Pn，直到Pn=0，其中Pn为不满足条件(2)的相邻两聚类的数目。最终在满足条件的聚类中选择最高频聚类作为目标模态，假设其幅值和频率分别为akp和fkp，则正弦辅助信号的幅值和频率为ak=akp，fk=fkp。

在信号分解中，通过移动正弦函数的相位θk，模态分离结果中的辅助信号被去除，同时保留了更多分离模态的细节信息。相位平移量可表示为

(3)

式中：N为平移次数。

2 规范变量残差分析

2.1 规范变量残差分析

规范变量分析是一种基于最小状态空间的动态监测方法，其目标是寻找一种线性组合使两组变量间的相关性达到最大。考虑到时间序列相关性，在k时刻处将观测向量yk分别以长度为p和f的时间序列表示，得到过去和未来观测向量yp,k和yf,k[14]

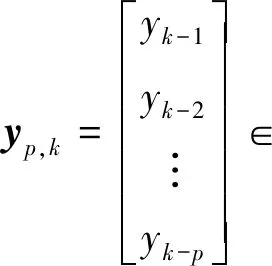
(4)

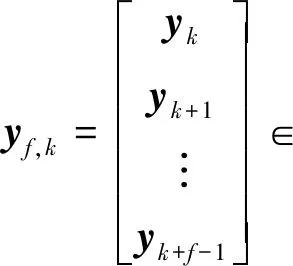
(5)

式中：m为每个时刻的变量个数，每个向量的零均值形式表示为

(6)

(7)

(8)

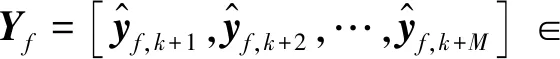
(9)

式中：M+p+f-1=N，N为观测序列的长度。

矩阵Yp和Yf的方差矩阵和协方差矩阵可分别定义为

(10)

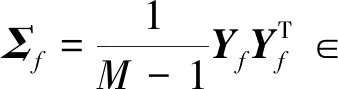
(11)

(12)

对矩阵H执行奇异值分解，提取变量间的潜在关系

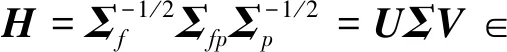
(13)

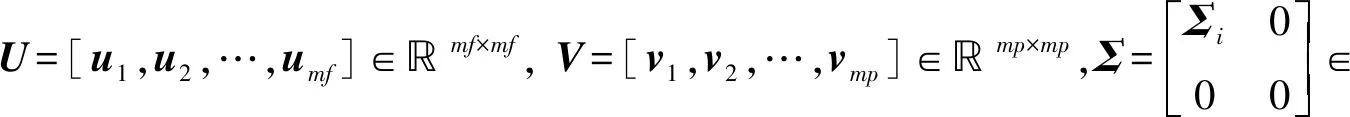
(14)

(15)

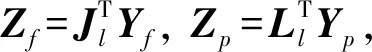
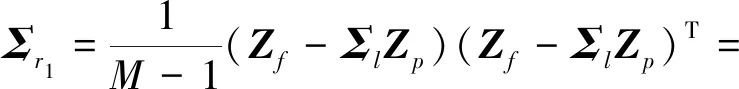
(16)

2.2 核密度估计

SEMD将冲击信号x(t)自适应地分解为由高频到低频排列的固有模态ck(t)，k∈[1,K]，则有

(17)

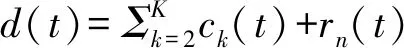
(18)

式中：p(x)为x的概率密度函数，可由核函数K(·)来估计。

(19)

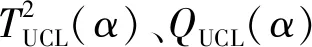
(20)

(21)

当任意一种指标大于安全阈值即可认为系统异常，逻辑关系式可表达为

(22)

式中： “⊕”表示“或”运算。当Gk=1时则认为系统故障并产生报警。当高速自动机监测指标处于安全阈值下方时，说明武器系统处于健康状态；当监测指标达到并大于参考阈值，表明高速自动机系统出现故障。此时应该制定合适的维修策略对武器系统进行检修，阻止劣变趋势进一步恶化蔓延。

3 高速自动机分时段动态特性监测

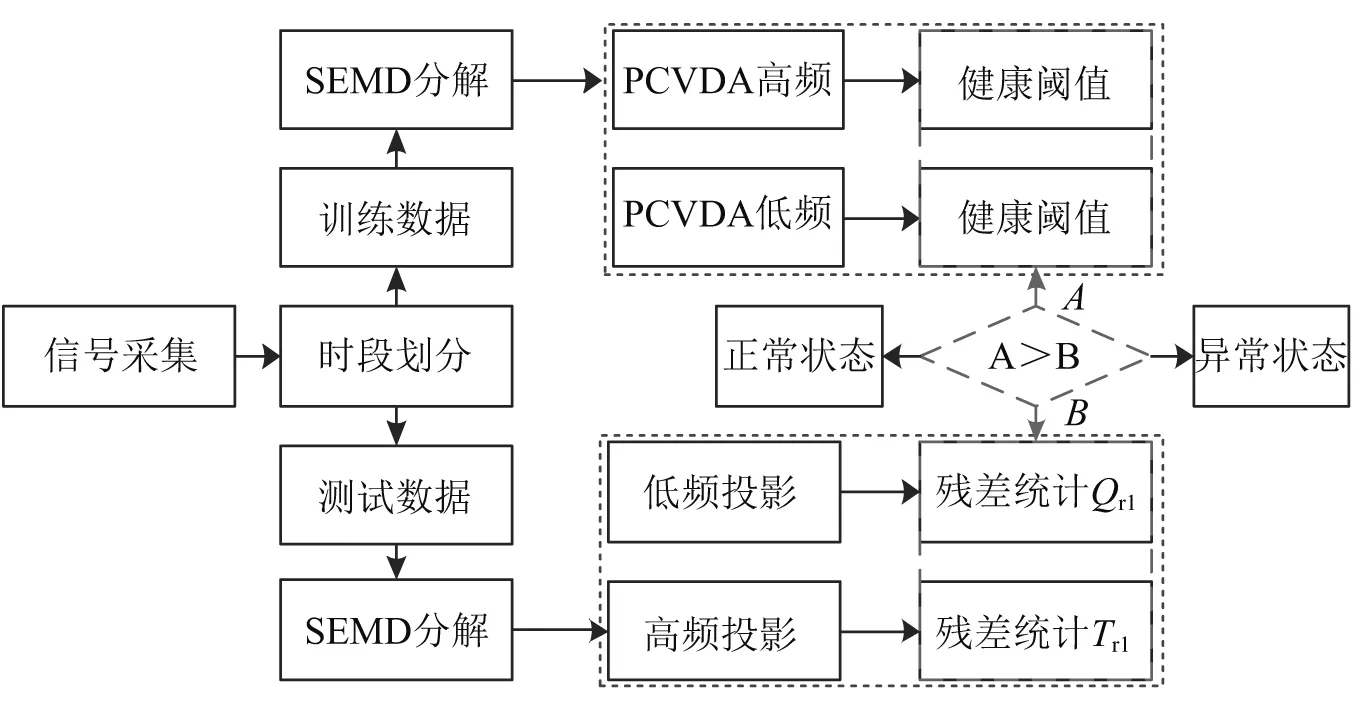
图1 高速自动机动态特性监测流程图Fig.1 The flowchart for dynamic performance monitoring of high-speed automata

3.1 短时瞬态冲击信号采集

闭锁片在枪弹发射时要承受剧烈冲击，使火药燃烧的高压气体大部分作用于弹头，在高温、高压和高冲击连续作用下，闭锁片成为高速自动机系统最容易发生故障的部位之一。此外，枪机在枪机框后座和复进冲击过程中也容易出现裂纹故障。本次射击试验分别收集高速自动机三种状态下短时瞬态冲击信号，即闭锁片故障、枪机故障和正常状态。第一种故障为闭锁片圆角旁深2 mm的裂纹，第二种故障为枪机圆角处深1.5 mm的裂纹。高速自动机在每种状态下的射击试验安排如下：五连发一次，三连发两次。因枪弹击发和枪机框后座时产生的冲击振幅最大，有利于获取高速自动机敏感的状态信息，本次试验的测点选择在枪弹击发和枪机框后座位置，他们分别位于枪匣的左侧上方和机枪尾部。以枪管指向为x轴方向，将两个加速度传感器固定在高速自动机测点位置测量水平与垂直方向的冲击信号，试验中使用LMS数据采集系统收集每种工况下高速自动机振动冲击数据，采样频率设定为204.8 kHz。高速自动机测试环境如图2所示。

图2 高速自动机试验台及两种故障状态Fig.2 The high-speed automata test rig and two failure types

本次试验数据取自枪机框后座位置处沿x轴方向的冲击信号，同时剔除每组射击中首发冲击信号，排除人为触发因素的干扰。因此，每种状态共收集4个冲击信号样本。

3.2 短时瞬态冲击信号的时段划分

高速自动机的运动过程主要由复进和后座两大子行程构成，即火药燃烧的部分高压气体通过导气管推动枪机框后座并压缩复进簧，期间完成闭锁片开锁、拨弹等行程；复进簧受压后推动枪机框复位，复进过程中完成推弹入膛，闭锁片闭锁等行程，如此循环往复。开闭锁行程中部件运动形态示意图，如图3所示。机框、枪机和闭锁片构成了一个运动子系统，枪机框在后座和复进行程中撞击闭锁片，完成开锁与闭锁两种形态的切换，部件间的撞击行为带来一系列的冲击振荡。

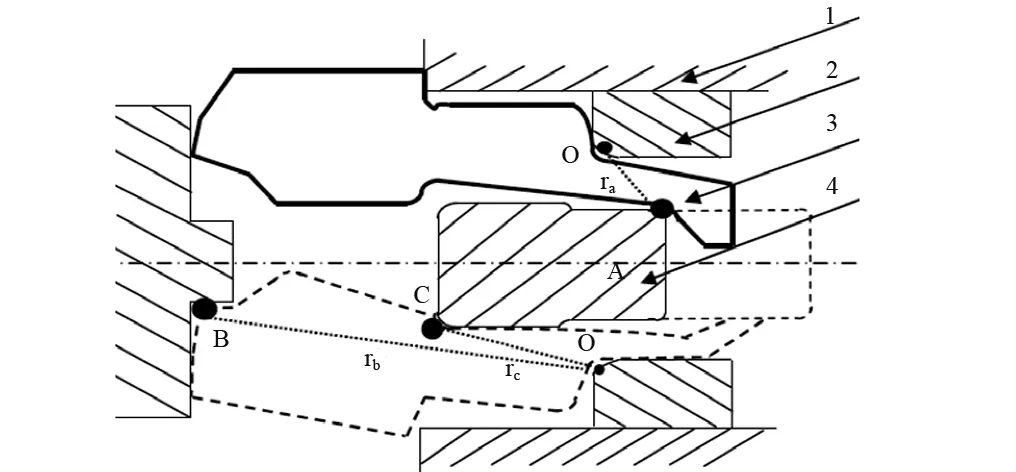
1. 枪机 2. 机匣 3. 闭锁片 4. 机框 图3 开闭锁行程示意图Fig.3 Schematic diagram of opening and locking strokes

图4(a)为高速自动机五连发冲击信号样本。单发的冲击信号如图4(b)所示。由图4可知，各部件在运动传递过程中伴随剧烈冲击，因部件间存在间隙及自由行程，冲击幅值瞬间达到最大后，又快速衰减到水平轴线附近(幅值约为0)。高速自动机的运动形态随着时间不断变化，且具有多行程特点，运行状态由一个子行程转到另一个子行程中，不同行程的冲击信号往往蕴含不同的相关关系。 高速自动机系统故障时，将引起行程间冲击信号的相关关系的改变。

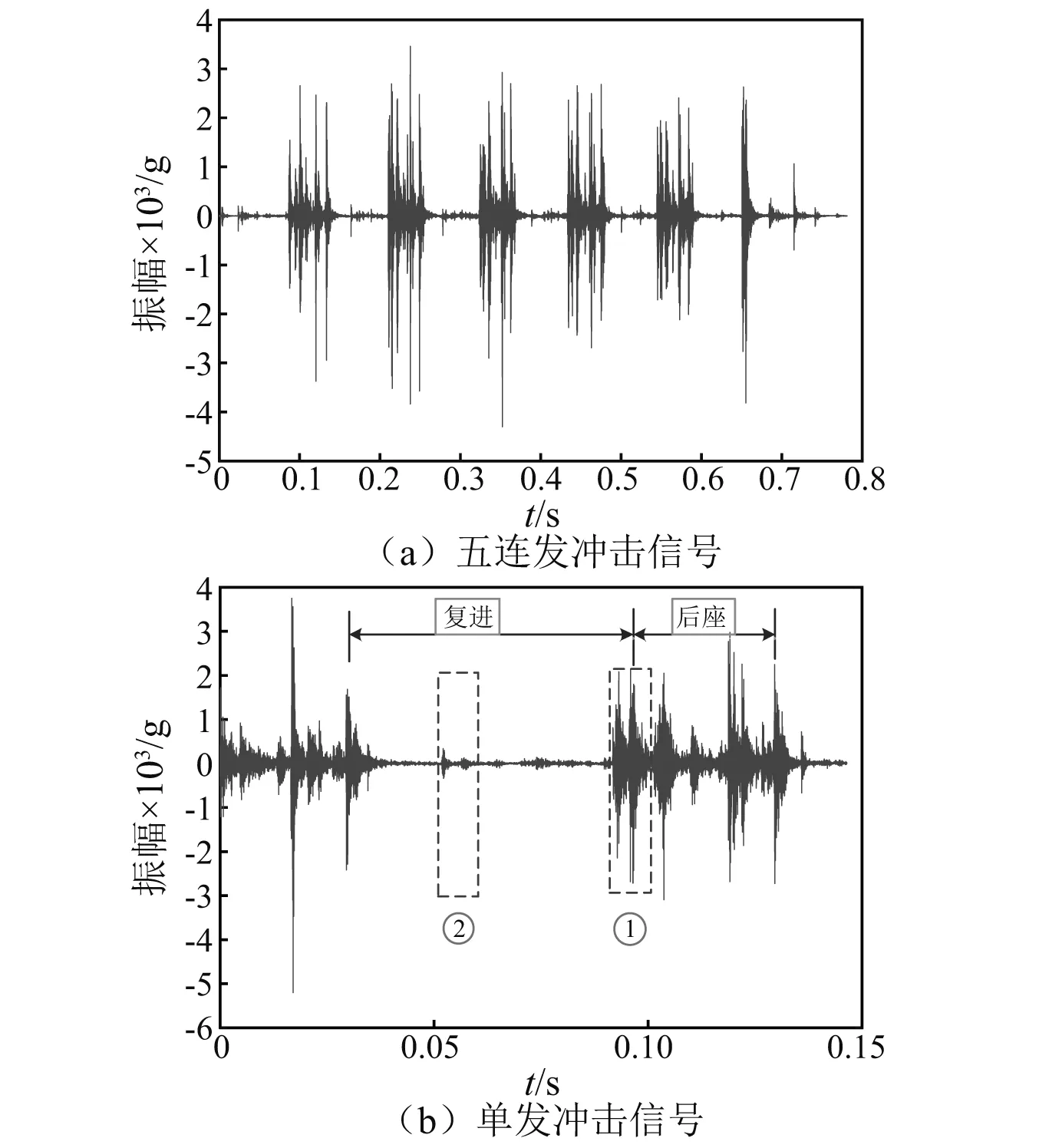
图4 短时瞬态冲击信号Fig.4 Short-term transient shock signals

通过分析和利用高速自动机的运动特性，可以建立各行程与冲击信号的对应关系，将冲击信号划分为不同的子时段。将时段1划入开闭锁行程，开闭锁动作和枪机动作都发生在该行程；将时段2划入推弹行程，该行程发生在枪机框复进行程，在推弹入膛过程中产生冲击振荡。因两种行程前后都有一段自由行程，表现在冲击信号上就是撞击后冲击幅值的衰减过程，于是每个子时段各取10 ms 用于高速自动机的动态特性监测(见图4(b))。

3.3 开闭锁行程状态监测

按照图1所示步骤，根据高速自动机运动特性对冲击信号进行时段划分，将开闭锁行程的健康数据和测试数据分解为高频和低频信号，如图5所示。 以健康数据的高频信号建立CVDA模型，确定规范变量空间的投影矩阵以及安全阈值，将测试数据的高频信号投影到过去及未来规范变量空间，并计算两者之间残差及其统计量；同理，可以建立高速自动机在低频部分的CVDA监测模型。

图5 行程1正常状态信号Fig.5 Normal shock signals of stroke 1

枪机故障时开闭锁行程的动态特性监测结果，如图6所示。其中时间序列长度p和f取p=f=25，保留的规范变量数目l=15。结果显示开闭锁行程中各部件正常状态时的统计指标低于安全阈值，枪机故障时统计指标沿着正常统计量上下波动，冲击处的峰值显著增大且超过安全阈值。高频段CVDA模型和低频段CVDA模型都反映了枪机正常与异常状态时系统动态特性差异，CVDA成功监测到枪机故障时的系统冲击特征。

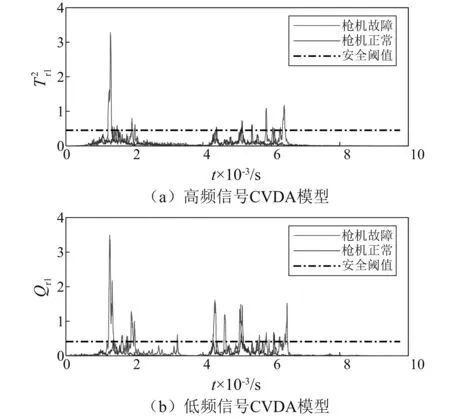
图6 枪机故障的动态特性监测Fig.6 Dynamic characteristic monitoring for failure of firearm bolts

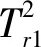
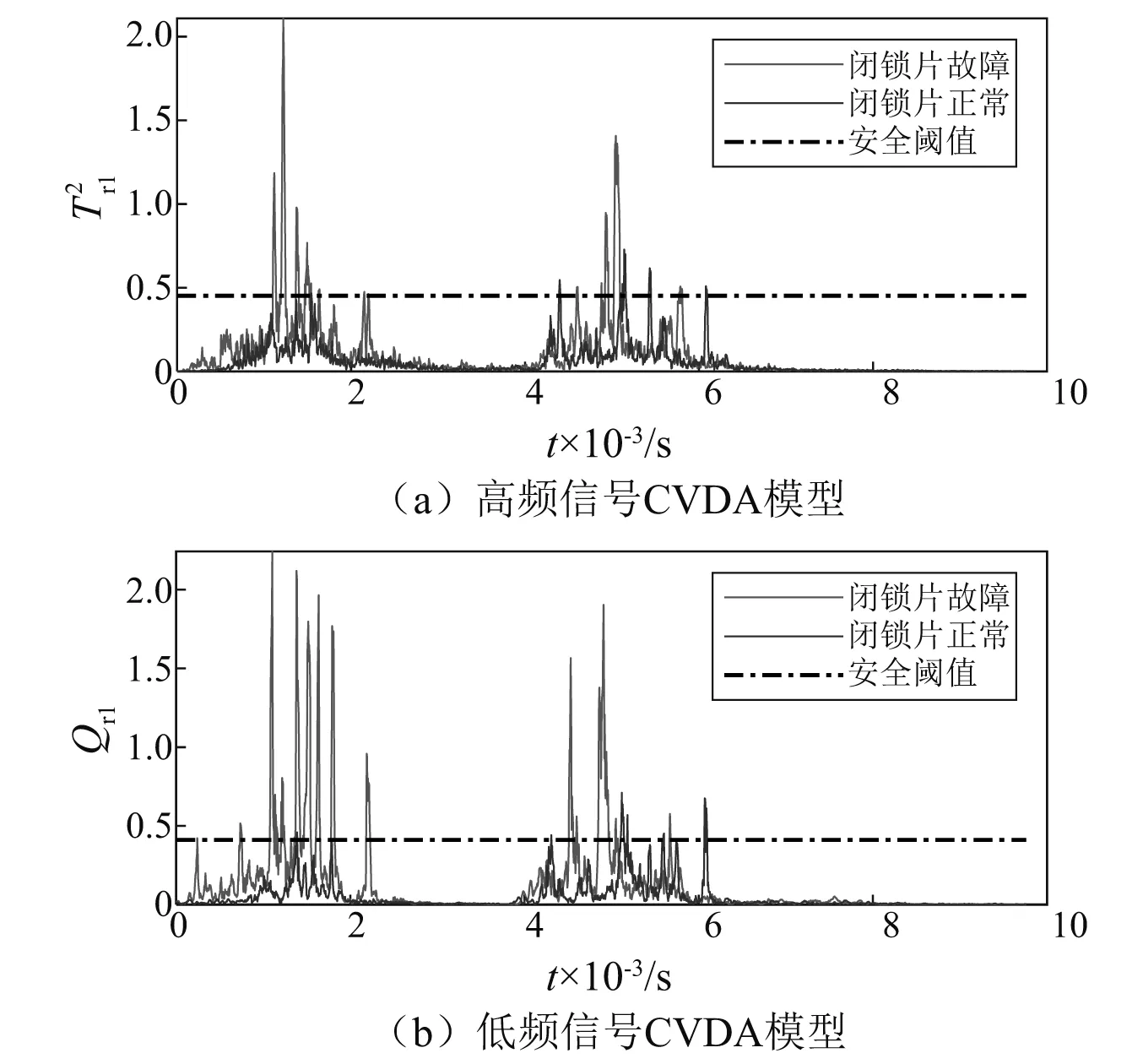
图7 闭锁片故障的动态特性监测Fig.7 Dynamic characteristic monitoring for failure of locking lugs

3.4 推弹行程状态监测

推弹行程中枪机推动枪弹入膛，枪机发生故障时，与该行程对应的时段2中也将产生动态特性异常的冲击特征。按照图1所示步骤，继续监测时段2中高速自动机的动态特性。行程2正常状态时的高低频信号，如图8所示。

枪机故障时推弹行程的动态特性监测结果，如图9所示。其中时间序列的长度p和f仍取p=f=25，保留的规范变量数目l=15。从图9可知，枪机正常时推弹行程的两次冲击幅值均低于安全阈值；枪机故障时，由于推弹时的撞击行为，2 ms位置处的冲击幅值骤然增大，同时超过安全阈值(见图9(a))，之后快速衰减至水平轴线附近。对低频信号建立的CVDA模型同样体现了这一点(见图9(b))。监测结果进一步证实了分段式CVDA对高速自动机动态特性监测的有效性。

图8 行程2正常状态信号Fig.8 Normal shock signals of stroke 2

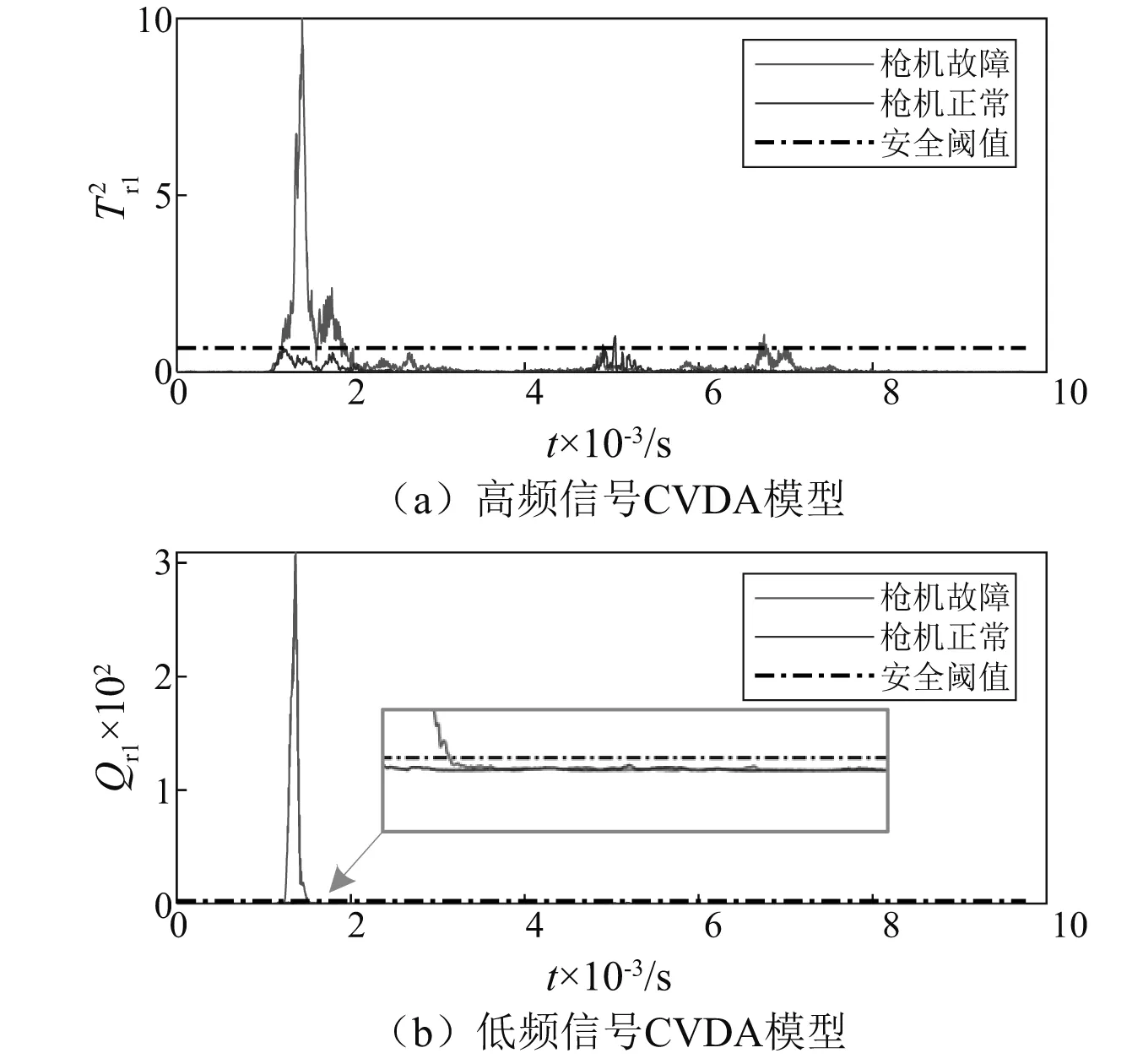
图9 行程2动态特性监测Fig.9 Dynamic characteristic monitoring of stroke 2

4 比较研究

(23)

(24)

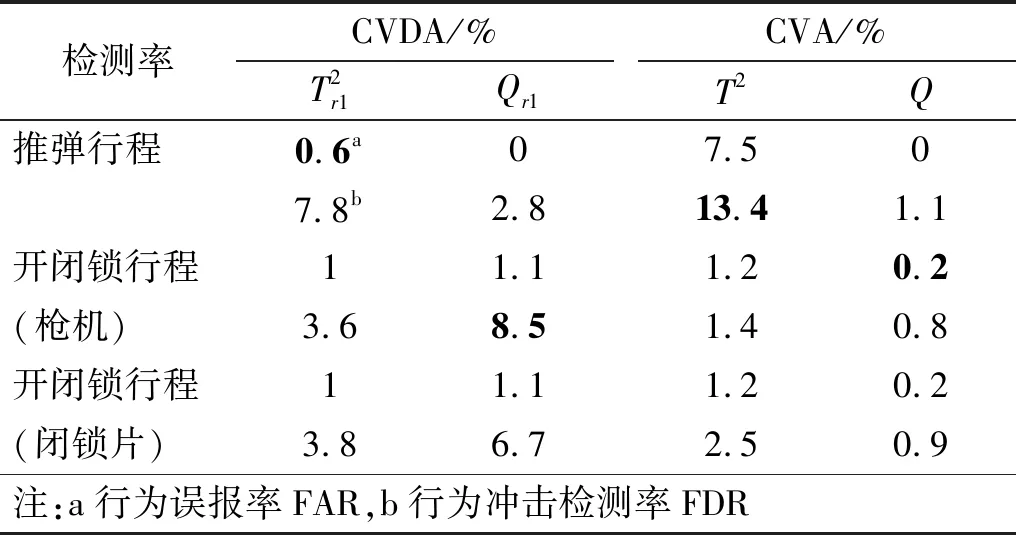
表1 两种方法的检测率比较Tab.1 Detection rate comparison of two approaches

5 结 论

提出一种分段规范变量残差分析模型监测高速自动机系统动态特性。分析了高速自动机系统运动形态，并建立其与短时瞬态冲击信号的对应关系，将冲击信号划分为一系列子时段。SEMD自适应地将冲击信号分解为高频和低频两部分，分别建立高频段和低频段的CVDA模型监测高速自动机每个时段的系统动特性。实验结果表明：

(1) PCVDA模型可以准确监测到高速自动机故障冲击特征。从高速自动机的运动特性出发，将运动形态划分为一系列子行程，建立各行程与冲击信号的对应关系作为信号时段划分的依据。PCVDA能够更精确地反映高速自动机的动态特性，为武器系统健康监测提供了一种可行方案。

(2) 为应对高速自动机各部件状态信息与强背景噪声混叠带来的冲击监测难题，采用SEMD将短时瞬态冲击信号转化为高频和低频成分，从高频和低频两方面提取微弱的故障信息，有利于提高高速自动机动态特性监测效率。

(3) 综合分析冲击检测率和误报率，PCVDA模型比CVA模型更能够提供具有竞争力的动态特性监测结果。