基于混合动态罚函数改进协同优化算法的船舶结构静动力学优化设计
郭天奇, 夏益美, 王福花, 王德禹
(1. 上海交通大学 海洋工程国家重点实验室,上海 200240; 2. 高新船舶与深海开发装备协同创新中心,上海 200240;3. 中国船舶及海洋工程设计研究院,上海 200240)
对于许多大型复杂系统涉及到的最优化问题,其目标函数往往需满足一系列不同学科的约束,且各子学科之间相互影响和作用,具有耦合方式复杂、维度较高、变量繁多等特点。技术发展的日新月异对各个学科间的相互耦合提出了更高的要求,多学科设计优化(Multidisciplinary Design Optimization, MDO)应运而生。MDO设计方法分为单级优化方法和多级优化方法,通过并行设计缩短周期,充分考虑了各学科间的耦合关系,从系统级的角度求解大型复杂系统的优化问题。
协同优化方法(Collaborative Optimization, CO)主要用于求解非层次型分解的MDO问题,具有很强的学科自治性,采用学科级优化器进行学科约束且支持并行处理,在船舶海洋结构物与航天器等分布式设计环境中应用广泛。CO方法可以把任何优化算法与已有的学科分析工具很方便地结合,每个学科都有着特定的优化器和适应子学科的优化算法。再者,CO方法中子学科约束条件与设计变量等只与本学科有关的优化信息都限制在学科级优化问题中解决,因此大大降低了各个子学科之间信息交换的难度。
近年来,许多学者对协同优化算法进行了深入研究,并针对其固有缺陷提出了一些改进方法。针对系统级一致性等式约束所导致的收敛困难问题,目前主要采用松弛因子法、罚函数法和响应面法三种方法进行改善。Alexandrov等[1]针对标准协同优化收敛困难的问题,提出了松弛因子法,松弛系统级一致性约束,但难以确定松弛因子的大小。Lin[2]针对系统级优化不满足KT条件的缺陷,提出了罚函数法以优化系统级目标函数,使CO算法的系统级转化为无约束优化,然而对罚因子的选取没有深入研究,在求解时严重依赖于初始点的选取。Sobieski等[3]提出了基于最优响应面的改进CO方法,显著降低了子系统优化的迭代次数。李响等[4]提出了基于超球近似子空间的协同优化方法,克服了已有梯度算法易发散、响应面方法计算量大等缺点,加快了收敛速度,但是忽略了需要严格满足的学科约束,降低了优化结果的可靠性。
针对以上对标准协同优化算法初步改进的不足,一些学者进行了更深入的研究。李冬琴等[5]结合外点法与内点法建立混合罚函数,提出改进的CO算法,实现了海洋供应船船型初步设计阶段的多学科优化,避免了收敛困难的问题。李海燕[6]采用动态罚函数方法,将系统级优化转化为无约束问题,并采用遗传算法优化系统级,减少了初始点选取的敏感性,但是收敛速度较慢。杨丽丽等[7]提出一种CO-PE全局多目标组合优化方法,并应用到多目标多约束的卫星结构优化问题中,良好的优化结果证明了算法的高效性和准确性。钱杨等[8]提出分段动态松弛协同优化算法(Sectionalized Dynamic Relaxation Collaborative Optimization, SDRCO),系统级先采用遗传算法进行全局搜索,再采用Hooke-Jeeves算法进行局部优化,避免了对初始点选取的依赖性,但两段松弛因子系数取为常数对系统级与学科级间的约束不够。柳明星等[9]利用一致性约束信息构造指数形式的动态自适应罚因子改进协同优化算法,对火星探测器的遥感性能和总重进行多目标优化,优化结果验证了该算法的可行性和有效性。谢琦等[10]采用自适应混合罚函数法,系统级运用GASA混合智能优化算法,提高了CO算法的全局搜索能力,避免优化解陷入局部最优,然而该方法的学科间不一致信息没有得到足够的控制。周奇等[11]采用两种不同的基于差异信息的动态可调罚系数,平衡一致性约束与目标函数之间的关系,并把该改进后的算法成功应用到以油船造价为目标的多学科优化问题中。
本文针对CO算法难以满足一致性约束条件导致收敛困难,以及CO算法优化结果易陷入局部最优的问题,提出了基于混合动态罚函数的改进协同优化算法。该方法不仅有着极好的全局搜索能力,解决了初始点选取的问题,避免陷入局部最优;同时采用引入松弛因子构造混合动态罚函数的方法,解决了标准CO算法固有的收敛困难的缺陷并显著减小了学科间的不一致信息。本文将该改进算法应用到船舶机舱的优化设计中,通过对比基于动态罚函数CO算法的机舱优化结果,验证本文基于混合动态罚函数改进的CO算法的收敛性、准确性和高效性。
1 协同优化算法
1.1 标准协同优化算法
CO算法把优化问题分为系统级和多个并行的学科级,CO算法的系统级一致性约束以及学科级一致性目标函数的表示通常采用二次平方和形式。假设系统优化问题分解为n个子学科,则标准协同优化算法的数学模型如下。
(1) 系统级数学模型

(1)

(2) 学科级数学模型
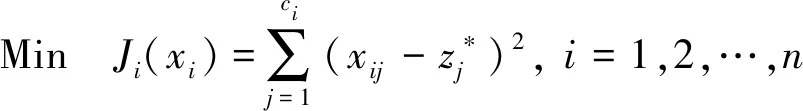
(2)
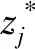
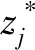
1.2 协同优化算法的缺陷及原因
然而CO方法仍有许多不够成熟需要改进的方面。在系统级优化时,Lagrange乘子不存在或是在最优解处学科一致性约束的Jacobian矩阵不连续,导致CO方法中的系统级优化不满足Kuhn-Tucker条件,因此系统级优化中采用的一致性等式约束在通常情况下很难满足,系统级优化问题的可行域可能不存在,最终导致优化收敛困难;另外,由于CO方法的优化结果对初始点的选取很敏感,因此很可能产生局部最优解。
对于标准协同优化算法,系统级需满足的Kuhn-Tucker条件如下
(3)

2 基于混合动态罚函数的CO算法
2.1 引入自适应松弛因子
松弛因子方法的作用在于把系统级一致性等式约束转化为不等式约束,降低协同优化算法的收敛难度。本文采用李响等基于超球近似子空间CO方法中的动态松弛因子设定,系统级约束转化为
(4)
式中:s代表超球近似子空间中两个高维球的半径,令
s=λΔ
(5)
式中:λ为常数, 且0.5≤λ≤1,该值保证了系统级优化朝着学科间不一致信息不断减少的方向进行。Δ定义为学科间不一致信息,令
Δ=max‖Xi-Xj‖
(6)
本文不一致信息Δ取2范数形式。
以距离最远的两个子学科最优点Xi和Xj为中心,s为半径的两个高维空间中的球,而松弛后的系统级可行域为这两个球的相交区域。本文松弛因子的大小根据学科间的动态不一致信息自动调整,不仅很好地满足了学科间的一致性,还兼顾了系统级优化过程中迭代计算的收敛问题,同时避免了对松弛因子大小的选择。
2.2 基于NSGA-Ⅱ与ASA组合算法的分段混合动态罚函数
本文针对标准协同优化算法易陷入局部最优的问题,根据船舶结构板材与骨材的特殊尺寸规格限制,采用全局与局部两段进行协同优化。由于遗传算法易早熟或是不收敛,对于参数和遗传算子的设置具有很强的依赖性;而模拟退火算法对初温的要求较高,抽样步数和搜索时间较长,因此本文系统级在全局优化阶段采用全局搜索速度较快的非支配遗传算法Ⅱ(NSGA-Ⅱ),在局部优化阶段采用收敛性较好且适合处理离散型变量的自适应模拟退火算法(Adaptive Simulated Annealing, ASA)。
2.2.1 全局优化阶段
全局优化阶段设计变量取为实数型,系统级采用全局优化速度较快的NSGA-Ⅱ算法确定全局解,学科级采用单目标优化算法多岛遗传算法(Multi-islands Genetic Algorithms, MIGA),同时基于全局阶段的混合动态罚函数方法,构造系统级无约束非线性目标函数如下
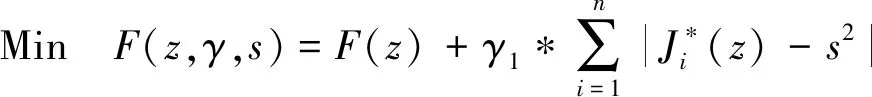
(7)
式中:a,b为常数,γ2为学科级传递给系统级的一致性约束,s代表松弛半径,四者共同决定了全局优化阶段罚因子γ1的大小。 本文取b=50,a=0.5, 自适应罚因子γ1随s,γ2的变化在迭代初期较大,该方法放宽了一致性约束,保证了在优化初期系统级可行域较大,最大程度上避免陷入局部最优并加速优化前进;在全局优化后期,系统级可行域减小,常数b依然可以保证对不满足一致性约束最优解的目标函数进行惩罚,严格控制了学科间不一致信息,实现全局收敛。
2.2.2 局部优化阶段
由于船舶结构板材与骨材尺寸的特殊规格,局部优化阶段的设计变量取为整数型,系统级采用收敛性较好的ASA算法进行局部优化,把全局优化的最优解取整后作为ASA算法的初温,学科级采用单目标优化算法多岛遗传算法(MIGA),同时基于局部阶段的动态罚函数方法,构造系统级无约束非线性目标函数如下
(8)
式中: 罚因子γ2为系统级与学科级间动态一致性约束,随着局部寻优的进行,优化结果逐步逼近最优点,γ2自适应减小惩罚项在目标函数中的权重,很好地实现了目标函数与一致性约束间的平衡。
由于罚函数法仅采用外点法不断逼近最优点,因此有时会陷入局部收敛,不能稳定地获得全局最优解,而本文基于混合动态罚函数改进的协同优化算法则较好地解决了这一问题。该方法的核心步骤如下流程,如图1所示。
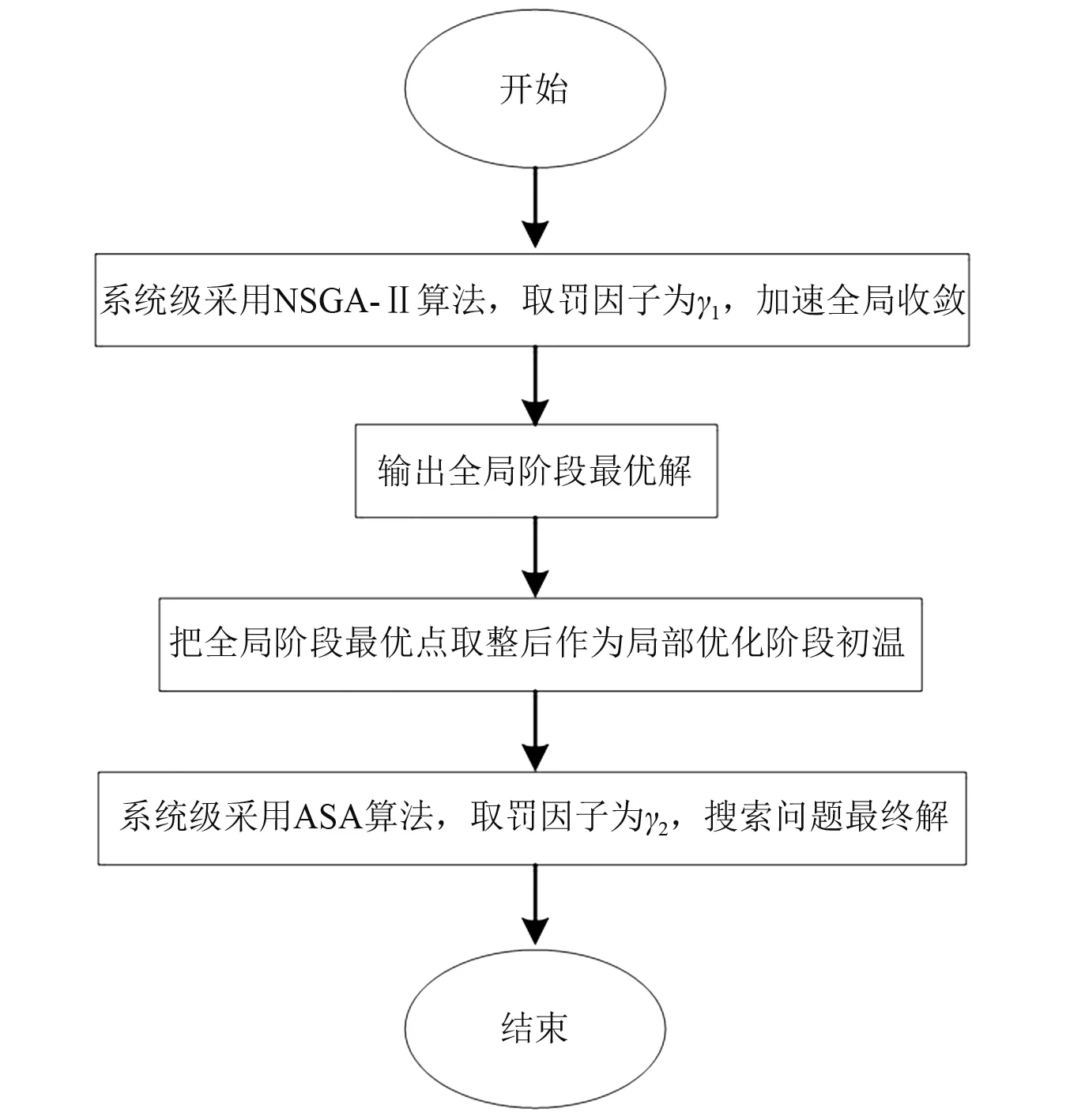
图1 基于混合动态罚函数协同优化算法流程图Fig.1 Flow chart of collaborative optimization algorithm based on the mixed and dynamic penalty function
3 船舶结构协同优化设计
把上述改进的协同优化算法应用到船舶结构上,对某船主机舱的静力学和动力学两个子学科进行多目标优化,并对比基于动态罚函数的CO算法与本文基于混合罚函数的CO算法的优化结果。
3.1 优化数学模型
本文所优化的船舶机舱模型模拟某实船机舱舱段,采用通用有限元软件patran建立,船长方向长度为21.8 m,船宽方向宽度为26.5 m,高度为7.9 m,包括甲板、双层底、舷侧、横舱壁、纵舱壁、平台等,如图1所示。网格大小纵向以肋位为边界,横向与垂向以纵骨间距为边界,一般网格长宽比不大于3∶1,纵骨、扶强材采用梁单元模拟,纵桁、强肋骨和强横梁的腹板用板单元,面板用梁单元模拟。主机两台各100 t,齿轮箱50 t和双层底水油100 t分别以质量点和MPC的形式加载在相应节点上。计算湿模态频率和动力学响应时,船体结构附连水质量以虚拟质量法加载在舱段与水接触的外底板单元上。

图2 船舶机舱结构有限元模型Fig.2 Finite element model of marine engine room structure
优化前,舱段结构总质量m为3 370.87 t,总体积V为74.56 m3;在规范静载荷作用下,最大正应力σmax为228.35 MPa,最大剪应力τmax为114.23 MPa;模态计算中,机舱结构的一阶固有频率f1为9.2 Hz;在主机激励作用下,机舱结构最大加速度响应amax为259.2 mm/s2,最大速度响应vmax为5.31 m/s, 最大位移dmax为0.092 mm。
本文利用“3.2”节所述的最优超立方设计进行灵敏度分析,共选出17个对两个子学科贡献率最大的设计变量,主要为有限元结构的板材厚度及骨材结构尺寸。静力学子学科对最大正应力与最大剪应力进行约束,动力学子学科对一阶固有频率、最大速度响应及最大变形进行约束。系统级以结构总质量m与最大加速度响应amax的加权和作为目标函数,本文偏重对最大加速度的动力学优化,因此设置质量的加权系数为0.4,最大加速度响应的加权系数为0.6;学科级分别以两个子学科一致性约束作为目标函数。本文基于混合动态罚函数改进的协同优化算法优化船舶机舱结构的具体数学模型如下
系统级:
(9)
静力学子学科:
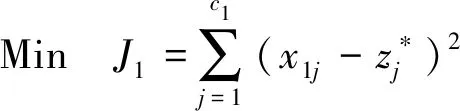
(10)
动力学子学科:
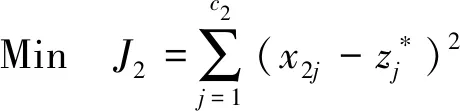
(11)
式中: 变量的物理意义如前所述,其中全局优化阶段γ取为γ1, 局部优化阶段γ取为γ2。
3.2 灵敏度分析
本文选定机舱有限元结构模型中板材的厚度及骨材的结构尺寸共计77个参数作为设计变量。由于拉丁超立方设计的试验点分布存在不均匀的情况,因此本文采用最优拉丁超立方设计(Optimal Latin Hypercube design)对船舶机舱的质量、正应力、剪应力、固有频率、位移响应、速度响应、加速度响应等静力学和动力学特性进行灵敏度分析,根据对静力学和动力学两个子学科的贡献率大小,分别选出贡献率前10个设计变量,其中学科间的耦合变量有3个,因此选取系统级优化设计变量共17个,具体编号如表1所示,具体名称如表2所示。

表1 船舶机舱结构设计变量汇总Tab.1 Design variable summary of marine engine room

表2 系统级设计变量Tab.2 Design variables of system level
3.3 近似模型构建
本文利用Isight作为优化软件集成有限元建模软件Patran和有限元计算软件Nastran进行迭代计算,由于学科级每次迭代都需调用有限元软件,且频响计算需要耗费大量时间,因此本文采用径向基模型(Radial Basis Functions, RBF)作为近似模型简化计算过程。RBF模型是以待测点与样本点之间的欧几里得距离为自变量,即假设y1,…,yN∈Ω⊂RN为一组输入向量,有下式
gi≡g(‖y-yi‖p),j=1,2,…,N
(12)
式中:gi是基函数, ‖y-yj‖表示欧几里得距离, 且0.2≤p≤3。
径向基模型可以方便地把多维问题转化为以欧几里得距离为自变量的一维问题,具有很强的逼近复杂非线性函数的能力,且允许异常样本点的输入,容错能力强。
3.4 机舱协同优化流程
本文根据“3.2”节所述的最优拉丁超立方设计方法对两个子学科进行灵敏度分析确定设计变量,根据“3.3”节所述的径向基近似模型方法简化有限元计算过程,利用Isight软件搭建协同优化流程。优化过程基于混合动态罚函数的方法构造无约束非线性系统级目标函数,系统级在全局优化阶段采用非支配排序遗传算法Ⅱ(NSGA-Ⅱ),找到一组全局最优解作为局部优化阶段自适应模拟退火算法(ASA)的初温,最终找到本文优化设计的最优解。本文船舶机舱结构的多学科协同优化流程,如图3所示。
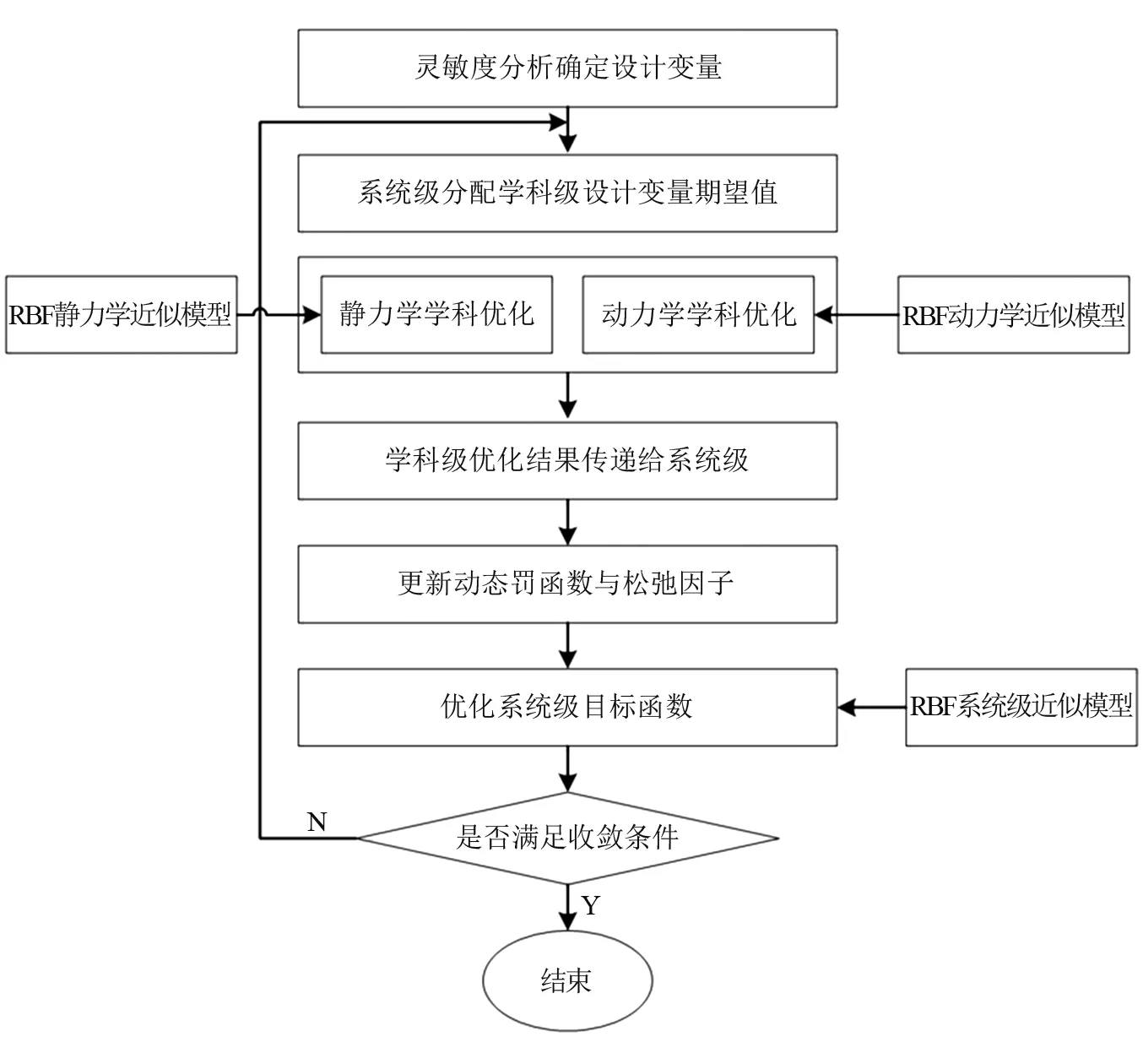
图3 船舶机舱结构多学科协同优化流程Fig.3 Flow chart of multi-disciplinary collaborative optimization on the marine engine room structure
3.5 优化结果与分析
根据本文设计的权重,分别采用周奇等基于系统级与学科级间差异信息的动态罚函数的CO算法与本文基于混合动态罚函数的CO算法对船舶机舱结构的目标函数进行优化计算。其中基于动态罚函数的CO算法,系统级采用非支配排序遗传算法Ⅱ(NSGA-Ⅱ),两个学科级采用单目标优化算法多岛遗传算法(MIGA)。
本文基于混合动态罚函数的CO算法优化目标函数的迭代过程,如图4所示。
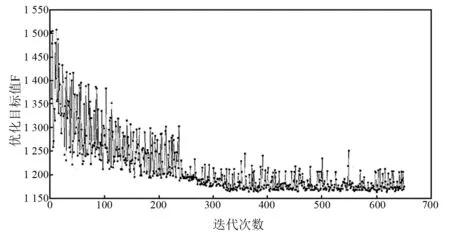
图4 基于混合动态罚函数的协同优化算法迭代过程Fig.4 The iterative process of the collaborative optimization based on the mixed and dynamic penalty function
基于动态罚函数的CO算法与本文基于混合动态罚函数的CO算法优化船舶机舱模型的优化结果对比如表3所示,各设计变量初始值和优化值结果,如表4所示。
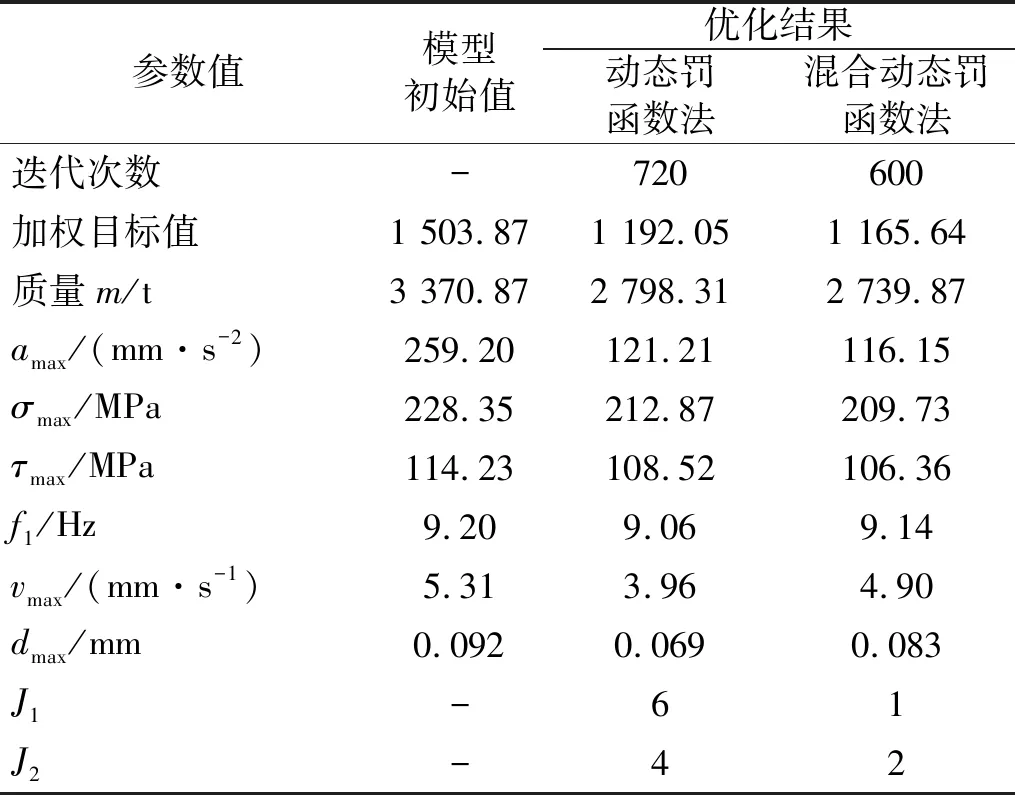
表3 基于两种算法的优化结果对比Tab.3 Comparison of results between two algorithms
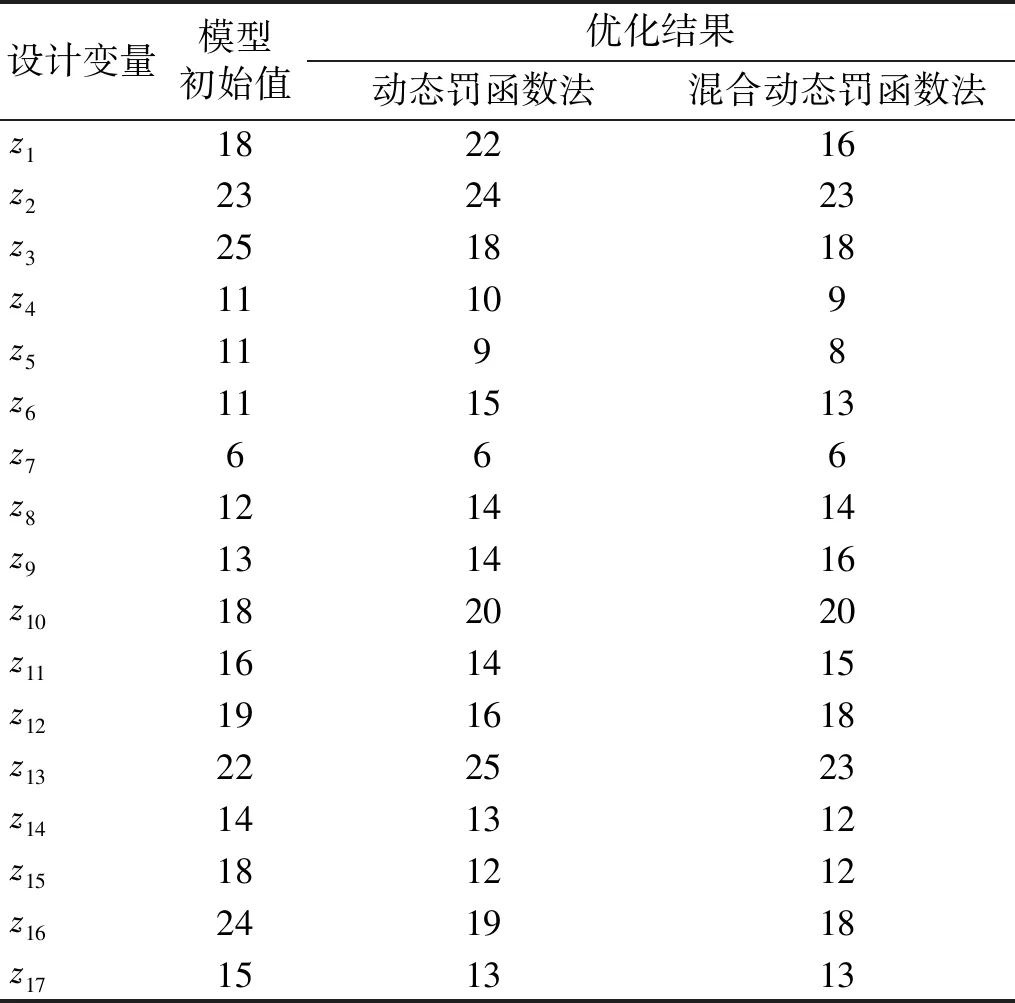
表4 基于两种算法的优化后设计变量对比Tab.4 Comparison of design variable after the optimization between two algorithms
由表3,4可以得出如下结论
(1) 本文基于混合动态罚函数的协同优化算法结构质量优化至2 739.87 t,相对模型初始值减小18.7%;结构最大加速度响应优化至116.15 mm/s2,相对模型初始值减小55.2%;加权目标函数值优化至1 165.6,相对初始值减小了22.5%,可见该算法的优化效果显著。
(2) 对比分析动态罚函数法与本文基于混合动态罚函数法改进协同优化算法的优化结果,一方面,本文达到收敛所用的迭代次数更少,收敛速度更快,这是由本文全局与局部两段引入松弛因子构造混合罚函数的特性所决定的,体现了本文改进算法的高效性;另一方面,本文算法下结构质量与最大加速度响应两个优化目标结果都更小,各静力学约束值更小,动力学约束值稍大但都在许用范围内,体现了本文优化算法的最优性。
(3) 本文在全局优化阶段的罚因子设计,重点约束学科间不一致信息;在局部优化阶段的罚因子设计,重点约束学科级传递至系统级的一致性约束条件,大大减小了系统级与学科级之间的差异性。从优化结果可以看出,本文改进CO算法的两个子学科与系统级之间的差异分别为1和2,较之基于动态罚函数CO算法的结果减小显著,体现了本文基于混合动态罚函数改进的CO算法更优的一致性约束控制及准确性。
4 结 语
本文针对标准协同优化算法收敛困难以及易产生局部最优解的缺陷,提出了两点改进方法。
(1) 提出基于混合动态罚函数的协同优化算法,该方法在罚函数中引入松弛因子,在初期放宽一致性约束,保证了较大的可行域和较好的收敛性,最大程度上避免陷入局部最优并加速优化前进;在后期严格控制一致性约束,保证收敛性的同时减小系统级与学科级间的差异。
(2) 在全局优化阶段采用全局搜索速度较快的NSGA-Ⅱ算法,在局部优化阶段采用收敛性较好且适合处理离散型变量的ASA算法,进一步避免了局部最优的产生。
将本文提出的改进算法应用到船舶机舱结构静力学与动力学特性的优化中,利用最优拉丁超立方设计方法进行灵敏度分析确定设计变量,并利用径向基近似模型方法简化有限元计算过程,最终得出机舱模型的最优解。对比原模型的目标值,该算法优化效果显著。再对比基于动态罚函数的协同优化算法,本文改进CO算法的优化结果与计算效率更优,且对一致性约束条件有着更好的控制。可见本文提出的基于混合动态罚函数的协同优化算法优化效果良好,是一种行之有效的多学科设计优化方法且对于实际船舶工程中的多目标多学科结构优化具有很好的应用价值。

